问题驱动式的Bode曲线教学

宋海涛 王夏复 夏朝辉 张合新 郑玉航

摘要：本文主要采用问题驱动式方法对《自动控制原理》中的Bode曲线进行教学设计。从复杂系统建模这个具体的工程问题出发，逐层递进，讲述Bode曲线定义、推导绘制方法、逆向应用建模，完整展示提出问题—分析问题—解决问题的“闭环思想”。该教学方法培养了学生的理论与实践相结合的能力。

关键词：自动控制原理;Bode曲线;实验建模;教学方法

中图分类号：G642.0     文献标志码：A     文章编号：1674-9324（2019）18-0204-02

一、引言

《自动控制原理》是一门理论性和实践性很强的工程技术基础课程，该课程理论抽象、公式推导复杂，不易理解和掌握[1]。这就对教学提出了挑战，要求任课老师对教学内容进行合理设计，并采用科学的教学方法[2]。

Bode曲线，又称对数频率特性曲线，是控制系统的一种重要的几何曲线。它反映系统的频率特性，可以作为系统分析和系统设计的关键工具。但是，频率域概念抽象，传统的注入式教学模式效果一般。针对此缺陷，本文从实际工程问题出发，逐层递进，讲述曲线定义、推导绘制方法、逆向应用，注重理论与实践的结合，提高学生发现问题、分析问题和解决问题的能力[3，4]。

二、教学目标

通过本次课内容的学习，将达到如下教学目标：

第一，掌握系统的Bode曲线绘制方法（重点）;

第二，掌握利用Bode曲线对系统建模（难点）。

三、教学实施

1.问题的提出。舵机是机器人的重要执行机构，如图1所示，其结构比较复杂，包含电路、机械关系。为了对机器人整体进行性能分析和设计，需要获得舵机的精确数学模型。因此，舵机的数学模型很重要。

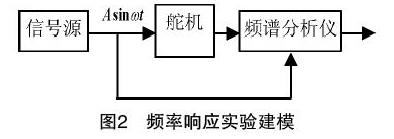
常用的建模方法是机理建模。但是，舵机的机理复杂，信号种类多，信号转换存在误差，建模结果不準确。因此，常采用另外一种建模方法——实验建模，原理如图2所示频率响应。

实验建模方法[5]。给舵机输入正弦谐波信号，由频谱分析仪采集输入输出信号，经相关计算后得到舵机的对数幅频和相频数据，然后进行相关处理，确定系统的频率特性，完成系统建模。其中，关键工具是Bode曲线。

2.曲线的定义（工具桥梁）。Bode曲线包含两条子曲线：对数幅频和对数相频曲线，两曲线的横坐标相同，都是半对数坐标系，即长度是lgω进行度量的。对数幅频的纵坐标定义为20lg|G（jω）|;对数相频的纵坐标为∠G（jω）。

3.典型环节的曲线（基础）。一般的控制系统可看作是由一些简单环节串联构成的，这些简单环节称之为典型环节。常见的典型环节有：比例环节、积分环节、惯性环节、一阶微分环节、振荡环节和二阶微分环节。对应频率特性及曲线参见[5]，它们的对数频率特性直接影响系统整体的对数频率特性。

4.系统的开环曲线绘制（理论基础）。一个系统的对数幅频特性是多个典型环节的对数幅频特性叠加，而在转折频率段内，典型环节的对数幅频渐近特性曲线斜率不变化，则系统的对数幅频特性的直线方程也应该保持不变。那么，系统对数频率特性曲线中的对数幅频曲线应该是分段直线。则可以根据转折频率绘制系统的对数幅频特性曲线，此法称为按转折频率分段计算法。

最小的转折频率以左的频率范围称为低频段。对系统频率特性求极限推导，可得低频段L（ω）的直线方程为L（ω）=20lgK-υ×20lgω。基于低频段曲线，再利用分段直线的变化规律就可以绘制其他频段的曲线。在后面的绘制中，每遇到一个转折频率后，系统就叠加上其对应的典型环节的影响，直线斜率就会发生变化，变化的规律就取决于该转折频率对应的典型环节的特性，则得到分段直线的方程。

对于对数相频特性曲线的绘制，需要列写出系统相频的表达式，采用描点法绘制。

此部分根据模型绘制曲线，这个过程能否反过来呢？是可行的，这种逆向思维给我们提供了系统建模的一个重要方法：模型辨识。

5.曲线逆向应用（解决问题）。模型就是频率特性，分为K、υ、惯性环节、一阶微分环节等要素。而这些要素分别由曲线的低频段和其他频段决定。低频段的方程取决于K，υ，那我们根据低频段曲线就可以确定K，υ;其他频段的各转折频率及各折线的斜率则反映了系统含有惯性环节、一阶微分环节等各典型环节的信息。这样就可以最终确定系统的频率特性。所以，如果能够获得系统的对数幅频曲线，就可以确定系统模型，即模型辨识。而对数幅频曲线可利用频率响应实验得到。

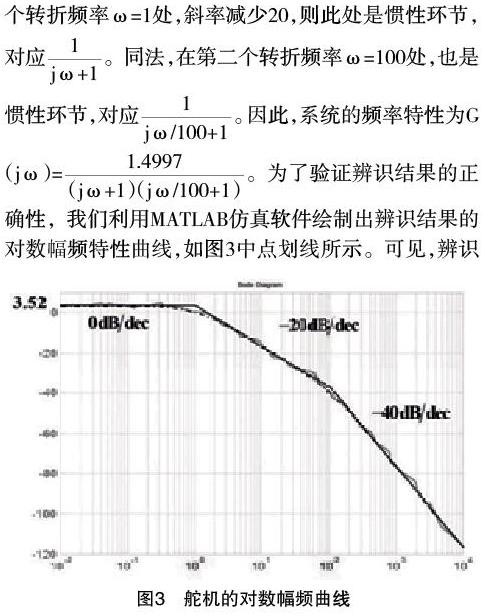
下面通过一组舵机频率响应实验数据来对舵机进行实验建模。首先，根据实验数据，描点得到舵机的真实对数幅频曲线，如图3中粗虚线所示。可见，真实对数幅频曲线不是直线、折线，这是因为实验设备测量噪声、干扰。经过去噪、分段拟合处理，得到如图3中粗实线所示的对数幅频渐近线。

可见，对数幅频渐近线大约有三段，利用渐近线可在图上测量出其低频段幅值、各分段的斜率、转折频率。低频段幅值为3.52，斜率大小分别是0，-20，-40，转折频率为1、100。

四、总结

本节课以复杂系统的模型辨识问题为驱动，讲述控制系统频域的一个重要曲线——Bode曲线的绘制和应用，问题驱动式的教学思路完整展示提出问题—分析问题—解决问题的“闭环思想”。教学内容和教学方法体现复杂数学模型与简洁几何曲线的数形结合思想。在曲线绘制部分，根据系统模型推导，发现曲线是由低频段关键要素K，υ和其他频段的转折频率决定。在曲线的逆向应用部分，利用对数幅频曲线与数学模型的一一对应关系，解决系统建模问题。但是，这种一一对应关系仅适用于最小相位系统，如果系统为非最小相位系统，则需要同时结合相频特性。Bode曲线的实验建模应用，具有广泛的工程实践意义，有助于解决复杂系统的建模问题。

参考文献：

[1]白翔云，邹长春.浅谈自动控制原理教学改革与实践[J].时代农机，2018，（4）：123.

[2]林青，裘浔隽，张君，王金平，丁轲轲.以多种手段为导向的教学方法的实践及探讨[J].教育教学论坛，2018，（24）：167-168.

Abstract：This paper mainly uses Problem-driven method to finish the instructional design of the Bode curve in automatic control principle.Starting from the modeling of complex system，which is a specific engineering problem，this paper describes the definition of Bode curve，deduces the drawing method，and models with the reverse application.The whole process completely presents the closed-loop idea of raising problems，analyzing problems and solving problems.This teaching method trains the students' ability of combining theory with practice.

Key words：automatic control principle;Bode curve;experimental modeling;teaching method