基于空间网格模型的曲线箱梁预应力优化布置

汪学明，吴节松 （安徽宏泰交通工程设计研究院有限公司，安徽 合肥 230022）

随着我国经济的快速发展，交通建设行业的发展也越来越迅猛，受限于地形、地貌、环境协调性、美观性等要求，曲线梁桥[1-2]在山区公路、高速公路互通枢纽、城市立交桥中得到了广泛的运用，曲线梁桥以其简洁的身姿，优美的曲线成为一道道亮丽的风景线。

曲线梁桥不同于直线梁桥存在较大的扭矩，通常采用抗扭刚度大的箱型截面，而正因为采用箱形截面，这种显著的弯扭耦合效应同时还伴随着箱形截面的剪力滞效应、翘曲效应，使得结构的计算分析异常复杂[3]。目前主要的设计分析方法有两种，一是采用桥博、Midas等单梁杆系有限元软件分析计算，再考虑各种系数对荷载效应进行放大，这种方法简单方便，但无法准确考虑到截面剪力滞效应、扭转效应以及畸变效应，存在一定的不足，不能满足我们对精细化设计的要求，也无法让我们认知结构的真实应力分布和变形情况；二是采用ANSYS等三维实体有限元软件分析计算，这种方法能够准确的反映结构的真实应力和变形，但庞大的计算量以及复杂的建模过程和结果提取往往无法满足工程建设的需求，且对于预应力作用效应的等效模拟尚存在一定的失真[4]。针对以上问题，最新的公路混规提出了采用实用精细化分析模型来解决箱梁的空间效应问题，弥补单梁整体模型的不足。本文依托具体工程实例，采用Midas Civil空间杆系有限元软件建立曲梁的空间网格模型[5]（实用精细化分析模型之一），通过模型计算结果与现场实测数据对比，反映出空间网格模型的计算精度，同时借助空间网格模型提出曲线箱梁的预应力优化布置方法。

1 工程背景

某山区二级公路跨越河道采用3×30三跨一联的预应力混凝土现浇箱梁桥，由于地形限制，桥位线形位于R=100m的小半径曲线上，采用单箱单室截面，顶宽10m，底宽6m，悬臂2m，梁高1.8m。为了减少阻水面积，下部结构桥墩采用独柱墩，主梁采用C50混凝土，预应力采用6束19φ15.24 钢绞线（W1～W6）对称布置于腹板中，fpk=1860MPa，张拉控制应力为0.75fpk。桥梁采用鹰架现浇施工方法，施工时为方便施工控制及运营阶段健康监控，在边跨跨中、1号墩墩顶及中跨跨中腹板上下缘均布置了应力测试点，并在每跨1/4L，1/2L，3/4L及墩、台腹板顶布置了扰度观测点（采用电子水准仪进行观测）。桥梁结构布置及测点布置见图1、图2（A/B/C为应力测试点）。

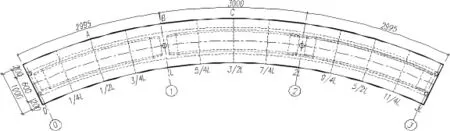
图1 桥梁平面布置图（单位：cm）

图2 箱梁横截面图（单位：cm）

2 空间网格模型

本次计算模型采用最新公路混规附录A推荐的空间网格模型，首先对箱梁截面按顶板、腹板、底板进行分割，再对顶板和底板进一步细化，由于腹板配有预应力，将腹板作为一个单元不再细分，分割后的截面如图3所示，然后运用Midas Civil大型空间有限元软件建立分割后的一个个离散截面的纵向梁单元，再分别建立顶、底板纵梁的横向连接，采用虚拟横梁[6]的方式。

图3 横断面网格划分（单位：cm）

图4 模型横断面单元

图5 空间网格整体模型

3 模型计算结果与实测值比较

3.1 竖向扰度

扰度取预应力张拉完成且支架拆除后的阶段，以内外侧腹板顶竖向扰度作为对比项，分别提取出相同位置模型计算的结果和现场实测的结果，同时与单梁模型的计算结果综合比较分析，如图6所示（以向上位移为正）。

图6 竖向扰度对比表

从图6可以看出桥梁内侧实测与计算的的竖向扰度均大于外侧，即桥梁整体处于向外侧扭转的趋势上，其中跨中处扭转最为明显，往桥台方向逐渐减弱，最后在桥台处扭转被双支座所平衡，全桥的弯扭耦合效应非常明显。同时本图显示出空间网格模型计算数据与现场实测数据高度的吻合，而单梁模型计算结果偏离实测较多，表明空间网格模型有较好的计算精度，单梁模型不能满足精细化设计分析的要求。

3.2 应力

应力同样取预应力张拉完成且支架拆除后的阶段，以测控截面内外侧腹板顶、底正应力作为对比项，分别提取出相同位置模型计算的结果和现场实测的结果，同时与单梁模型的计算结果综合比较分析，如表1所示。

应力对比表 表1

从表1实测数据和两组模型计算数据对比可以看出空间网格模型计算应力值与实测值基本吻合，而单梁模型误差较大（局部误差超过30%），表明空间网格模型的计算结果有较好的精度，单梁模型计算结果已然失真。

再从6网格模型和实测模型的数据可以看出桥梁外侧腹板上缘实测与计算的正应力均大于内侧，而下缘外侧腹板实测与计算的正应力均小于于内侧，这与外侧腹板的竖向扰度比内侧小的规律一致；同时表格显示各截面的内外腹板上下缘应力有明显的分布不均匀现象，说明曲线箱梁预应力布置方法尚存在不足；再通过对比3个截面的应力数值可以发现内墩顶处（B截面）应力及上下缘应力要小于跨中处上下缘应力，这主要由于墩顶处截面刚度较跨中处大造成的。此外网格模型计算值均比实测值稍偏大，表面桥梁的实际刚度比网格模型的刚度大，结构更偏于安全。

4 预应力效应及优化布置

众所周知，桥梁设置预应力的目的主要是为了抵消结构恒载产生的弯矩，并在结构内留存一定的压应力储备，以防止活载作用下开裂[7]。对于直线桥梁，预应力则可以等效为轴向力和竖向荷载，竖向荷载可与恒载相互抵消，轴线力能够提供压应力储备，然而对于曲线箱梁由于曲率的影响，预应力会对箱梁产生额外水平的径向力，而这个径向力又会根据预应力筋和箱梁剪力中心的相互位置关系产生扭矩，如下图所示。

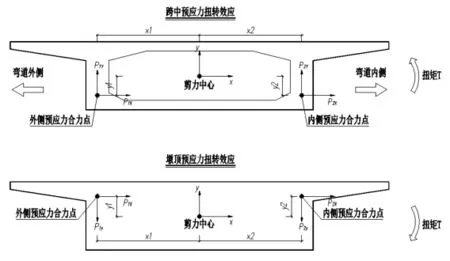
图7 预应力作用对箱梁产生的扭转效应示意图

显然从上图而已看出预应力作用在跨中位置产生向弯道外侧的扭转，在墩顶产生向弯道内侧的扭转。

基于曲线箱梁中的预应力作用效应特点，结合工程实际操作的可行性本文提出以下三种预应力优化调整方案，并运用空间网格模型进行计算分析：

方案一：在跨中增大x2，减小x1；在墩顶减少x2，增大x1，可采取预应力横向偏移腹板中心的方式实现，模型计算时偏移值取0.1m，如图8所示；

图8 预应力钢束偏离腹板中心示意图

方案二：在跨中减小 y2、y1；在墩顶增大 y2、y1，可采取预应力整体上抬的方式实现，模型计算按预应力整体上抬0.1m计算；

方案三：降低内侧预应力钢合力值，模型计算可采取降低内侧预应力钢束的张拉控制了实现，取内侧张拉控制力为0.70fpk；

为了更好的反映扭转效应的变化，我们引入无量纲变量“η”（η=内外侧腹板的竖向扰度差/腹板中心距×104）来反映扭转角度，提取模型在预应力张拉完成且支架拆除后阶段的计算结果如图9所示：

图9 箱梁扭转效应图

从图9可以看出三种方案均改善了箱梁的扭转效应，其中方案二（整体上抬预应力钢束合力作用点）效果最为明显，方案一的改善效果次之，方案三改善效果不明显。

再分别提取当前阶段各模型的控制截面应力值，进一步对比分析，如表2所示。

从表2中的应力变化可以明显看出三种方案对于应力分布不均现象的改善与扭转效应改善的效果基本一致，其中方案二的改善最为显著，方案一效果次之，方案三的改造效果不明显，且方案三内侧腹板的应力整体稍微减小，这主要是由于方案三的内侧预应力减小造成整体应力的下降。

应力对比表 表2

5 结语

本文通过曲线箱梁的具体工程实例建立了实用的精细化模型——空间网格模型，通过对比现场实测数据和模型计算数据以及调整预应力布置得到以下结论：

①空间网格模型的计算结果与实测数据基本吻合，有较高的精度。

②小半径的曲线箱梁的弯扭耦合效应非常明显，整体有向外翻转的趋势，截面内力分布不均匀。

③预应力作用对于曲线箱梁在跨中有增大扭转的趋势，在墩顶有削弱扭转的趋势，通过模型计算结果显示，对跨中预应力往外径方向偏移、墩顶预应力往内径方向偏移以及整体抬升预应力作用线均有利于改善结构的扭转效应和应力分布不均现象，调整内外侧预应力大小值对结构的扭转效应和应力分布不均现象的改善效果不明显。