基于BELL测量的随机数提取方案

李雪杨 昌 燕 代金鞘 张仕斌 郑 涛

(成都信息工程大学网络空间安全学院 四川 成都 610225)

0 引 言

现代信息社会的飞速发展，需要强有力的密码保护措施。现代密码学中，密钥的产生和分配是十分关键的内容[1]。香农的理论研究表明，只要某方案使用的密钥或随机数是完全随机的，且其与信息的长度一致，那么它就是绝对安全的信息保护方案[2]。随机数在保密通信、统计分析、数值模拟等领域均有广泛应用，随着信息技术的高速发展，计算能力不断提高，以伪随机数为密钥被破解的事件层出不穷[3]如何产生优质的随机序列具有重要的科研意义和应用价值。传统的基于数学和经典物理的随机数发生器生成的伪随机序列由于其可预测性，并不能使我们信息的安全性得到有效的保证。传统的物理随机数发生器多利用电阻热噪声[4]，单光子随机性[5-6]以及混沌电路[7]来提取随机数。

为得到绝对安全的真随机序列，近二十年来，基于量子的随机数发生器得到了各界科研学者的关注。随着量子理论和测量技术的发展，一系列基于量子的随机数发生器QRNG(Quantum random number generator)被提出[8]：1994年，基于单光子路径区分方案的量子随机数发生器被首次提出，其后又出现了基于光子数路径纠缠、基于单光子时间分辨等方案。

然而，在实际的随机数产生过程中，由于设备的限制，如采样设备、探测器设备中的噪声以及设备供应商在制造时人为采取的某些策略，我们获得的随机序列的统计特性受到了很大影响[9]。为消除原始序列的偏置，我们利用数学手段进行后处理，以保证序列满足均匀分布。基于von Neumann算法去偏置是一种常用的后处理手段[10]，通常应用此方案时需要随机制备4种Bell态粒子，再用Bell基测量Bell态粒子，最后利用von Neumann算法去偏置，由于随机制备粒子属于经典物理过程，缺乏很好的随机性，我们最后得到的序列不是真随机的。本文提出一种改进的随机数提取方案，借助对Bell态粒子执行联合测量后粒子坍缩状态的随机性以及von Neumann算法，使得初始序列拥有良好的随机性，从而有效地提高了最终序列的随机性。

1 预备知识

1.1 真随机数

真随机数是指随机数在无限长序列下具有如下性质[11]：

(1) 均匀分布：一串真随机序列满足均匀分布的统计特性，如序列的每一位是0或者1的概率相等，都为0.5。

(2) 不可预测性：真随机序列的每一位都是相互独立的，即使知道序列某一位的值，也不能预测或计算出后一位的值。

1.2 量子测量的不确定性

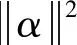
1.3 Bell态

4种Bell态可表示为：

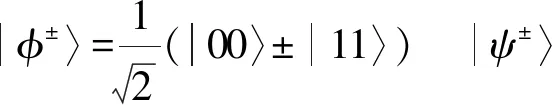
(1)

1.4 纠缠交换

纠缠交换的作用是将两个原本不纠缠的量子系统变成纠缠态[14]，假设粒子1、粒子2处于Bell纠缠态|φ+〉12，粒子3、粒子4处于Bell纠缠态|φ+〉34，整个系统态为|φ〉1234=|φ+〉12⊗|φ+〉34。

对粒子1、粒子3做Bell联合测量，粒子2、粒子4就会纠缠在一起：

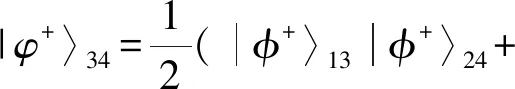
|φ-〉13|φ-〉24+|ψ+〉13|ψ+〉24+

|ψ-〉13|ψ-〉24)

(2)

系统态会以1/4等概率随机塌陷为4项之一，此过程物理随机且不可预测。此时，系统中粒子1、粒子3纠缠，粒子2、粒子4也因粒子1、粒子3的相互作用而纠缠。下面给出4种Bell态中任意两个作为初始态，执行纠缠交换后的塌缩组合如表1所示。

表1 纠缠交换塌陷态组合

续表1

2 传统的基于von Neumann算法的随机数生成方案

通常该方案如下：

(1) 随机制备n对4种Bell态纠缠粒子(|φ+〉，|φ-〉，|ψ+〉，|ψ-〉)。

(2) 对每对纠缠粒子进行Bell测量，随机获得4种结果|00〉，|01〉，|01〉，|10〉分别记为00,11,01,10。

(3) 采用von Neumann算法进行后处理：丢弃序列中连续相等的两个比特00和11，将01编码为0，将10编码为1，获得随机性较好的随机序列。

其中von Neumann算法的思想如下：

00=(1/2+ε)(1/2+ε)=1/4+ε+ε2

(3)

11=(1/2-ε)(1/2-ε)=1/4-ε+ε2

(4)

01=(1/2+ε)(1/2-ε)=1/4-ε2

(5)

10=(1/2-ε)(1/2+ε)=1/4-ε2

(6)

显然，丢弃00和11后，测得01和10的概率相同。但是随机制备4种Bell态粒子属于经典物理过程，缺乏很好的随机性，最终序列依赖于初始序列的选取，我们最后得到的序列不是真随机的。

3 改进的基于von Neumann算法的随机数生成方案

3.1 生成方案

保持von Neumann算法的思想不变，我们对上述应用做了改进，提出了新的随机数生成方案(表2给出了8对Bell态粒子产生随机数的具体过程)。

(1) 任意制备2n对处于4种Bell态的粒子(|φ+〉，|φ-〉，|ψ+〉，|ψ-〉)，此过程不必须随机。

(2) 每两对Bell态粒子为一组，将每组中每对Bell态粒子中的第一个粒子提取出来，进行联合Bell测量，获得测量结果。假设第一组的两对Bell态粒子处于|φ+〉12、|φ+〉34态，则将粒子1、粒子3提取出来进行联合测量后，会随机测得4种测量结果之一：|φ+〉13、|φ-〉13、|ψ+〉13、|ψ-〉13。

(3) 通过测量结果以及表1，得出纠缠交换中的剩余粒子的塌陷态组合，至此，就随机制备了Bell态量子序列S1。假设第一组中粒子1、粒子3的测量结果为|φ-〉13，参考式(2)，则对应剩余粒子2、粒子4的塌陷态组合为|φ-〉24，由量子测量的不确定性可知，随机数发生源S1不可预测，且为随机制备。

(4) 将随机制备的Bell态量子序列S1通过Z基进行测量，获得测量结果序列S2(S2的每一组取值简记为{00，01，10，11})。

(5) 由von Neumann的算法可知，只有01和10比特的概率分布相同，所以将S2中的00、11舍去，保留01、10，同时将01记为0，10记为1，最后得到n比特的最终序列S3。

听我这样说，一向沉稳的八叔也生气了：李六如，说假话面不改色心不跳。昏迷了能在合同上摁手印？就是你那个合同，李顺拿着挨家挨户宣传，说，六如叔三十年的合同都改了，你们那二亩地还舍不得。跟你们说，胳膊拧不过大腿，二期工程那是乡里的五大工程之一。李顺这么说，又有你那个合同，人们还怎么说，只好也签了字。一亩地赔了一万块钱。原来只说要建渡假区，还要安排工作，后来才知道要开发楼盘，一个平方就卖三四千块，咱这地等于白让那个佟老板给拿走了。

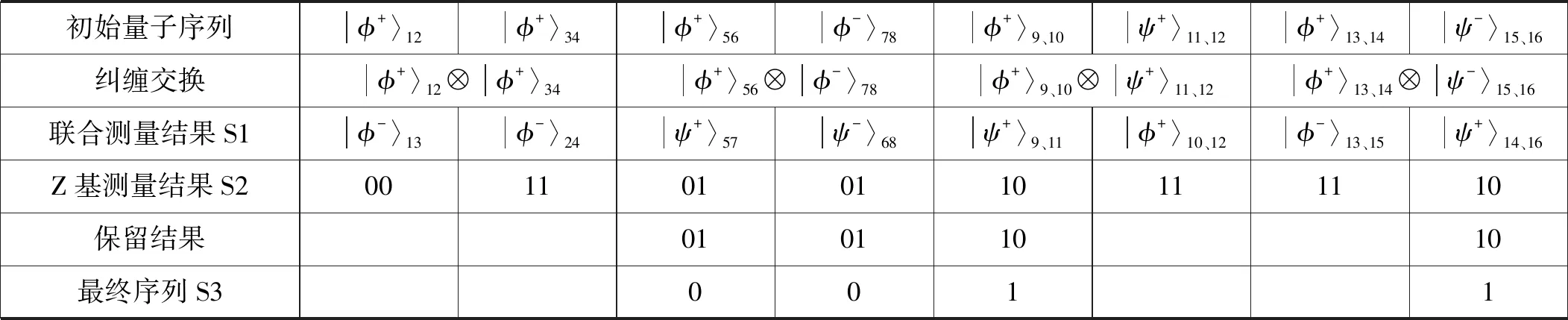
表2 随机数生成过程及结果举例

由表2可知，利用8对Bell态粒子，最后得到随机序列0011，效率为25%。上述过程的优点在于：Bell态量子序列制备的随机性完全依赖于纠缠交换，初始序列随机性得到有效保证；且输出数列的随机性完全依赖于量子测量，其统计均匀性得到von Neumann算法保证，因此最终序列的随机性得到提升。

3.2 本方案与传统方案的比较

在传统的随机数生成方案中，第一步选择四种Bell态这一过程并不随机，这导致了生成的随机数序列在严格意义上并不随机，而是可以用一定概率推测的序列。而本方案产生的随机数序列与Bell态的选择顺序无关，基于任意两对Bell态粒子的纠缠交换，产生新粒子的这一过程的随机性由量子纠缠的物理特性保证。因而本方案生成的随机数序列具有更好的随机性。

4 随机性分析

4.1 初始序列(随机数发生源)的随机性

传统的基于von Neumann算法的随机数生成方案，选择四种Bell态这一过程需要很好的选择随机性来保证初始序列的随机性。一个量子随机数发生器，在保证初始序列良好随机性的情况下，可以产生具有真随机性的序列。然而传统的基于von Neumann算法的随机数生成方案的初始序列在产生过程中不可避免地混入经典噪声，这些噪声不但造成信息泄露，被攻击者利用，还会大大降低初始序列的随机性，从而影响量子的测不准性。以随机制备Bell态为前提来生成随机数的传统方案，随机制备Bell态这个前提首先就无法保证是真随机的。因此，无论后续的随机数生成过程如何设计，最终序列依赖于随机数发生源的随机性，这种传统的基于源器件安全的假设的随机数生成方案难以保证生成的随机数是真随机的。

本方案通过纠缠交换产生结果的随机性，从理论上保证随机数发生源的随机性。本文提出的方案不以随机制备Bell态为前提，而是通过Bell态纠缠交换时随机坍塌的物理随机特性保证随机数发生源的随机性，理论上为真随机。

密度矩阵ρ可以描述测量后的量子态概率结果，经过测量后，量子态|φ〉以pi的概率塌缩到某个固定的|φi〉上，经过测量后量子态|φ〉所处的状态可以表示为:

(7)

因此，本方案初始序列的随机性可以通过纠缠交换后的密度矩阵来保证，以一组的两对处于|φ+〉12、|φ+〉34态Bell态粒子为例，则将粒子1、粒子3提取出来进行联合测量后，系统的密度矩阵为：

ρ=〈φ+|13ρ1|φ+〉13〈φ+|24ρ1|φ+〉24+

〈φ-|13ρ2|φ-〉13〈φ-|24ρ2|φ-〉24+

〈ψ+|13ρ3|ψ+〉13〈ψ+|ρ3|ψ+〉24+

〈ψ-|ρ4|ψ-〉13〈ψ-|ρ4|ψ-〉24=

〈φ-|13|φ-〉13〈φ-|24|φ-〉24+

〈ψ+|13|ψ+〉13〈ψ+| |ψ+〉24+

〈ψ-|ρ4|ψ-〉13〈ψ-| |ψ-〉24)

(8)

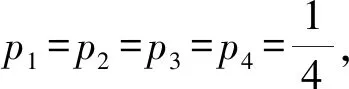
4.2 最终序列的随机性优化

由于噪声以及测量误差ε的影响，通常情况下，很难保证通过Z基的两种测量结果恰好等概率，此时初始序列还不具有均匀分布的统计特性。

为消除偏置，提高最终序列随机性，本方案采用von Neumann算法消除量子测量偏差。

将Z基测量结果S2经过von Neumann思想去偏置，去掉结果为00和11的结构，对于01和10只输出前一个比特。由式(5)、(6)可知，在考虑测量误差后，测得|01〉的概率与测得|10〉的概率相等，经过von Neumann算法，可以获得具有概率同为1/4-ε2的0比特和1比特，理论上保证了序列的均匀分布性，进而保证了最终序列的随机性。

由于设备限制，本方案目前难以在实验上给以证明，但在理论意义上，本方案既满足了随机源中4个Bell态的随机选取，消除了测量误差，最终序列的随机性相比与传统方案得到提高，又保证随机序列的制备效率。且制备简单，性能良好，量子序列的随机性可作为量子密钥的无条件安全性的保障。

5 结 语

本文对传统的基于von Neumann算法的随机数生成方案进行分析，提出了一种基于Bell测量的随机数提取方案。该方案应用Bell态粒子纠缠交换后粒子坍塌的随机性、量子测量的不确定性，保证了初始序列的随机性，并用von Neumann算法进行后处理，获得了随机性良好的随机序列。