自适应步长的Alpha-shape表面重建算法
2019-06-15李世林李红军
李世林 李红军
(北京林业大学理学院,北京,100083)
引 言
三维物体表面重建是获取三维空间信息建立该物体的三维模型,在3D城市、3D游戏等场景建模有着重要应用[1];在林业信息化测量中,利用重建的树冠形状,准确求解树冠体积、表面积和占地面积等信息量将会为绿地规划提供精确的数据支持[2];在现代临床医学中,通过重建出病人的骨骼或者肿瘤块,将会为医学诊断提供辅助手段[3];由于人类活动的日益影响,许多重要的古建筑古文物都遭受到了不同程度的破坏,对这些古建筑古文物进行数字化三维重建是文物保护的有效手段之一[4]。三维激光扫描技术的快速发展,使得人们能够快速地获取高精度、高密度的物体表面的三维点集。所以如何准确、快速地进行三维点集的形状分析和表面重建成为当前急需解决的重要问题。
国内外的专家学者已经针对二维和三维的点集形状进行了大量的工作。1977年,文献[5]首次以二维平面点集凸包的推广为基础,来刻画点集的形状;文献[6]给出了点集形状严格的数学定义;文献[7]以Delaunary三角化为工具,采用搜索算法来“雕刻”三维点集的单连通形状,称为雕刻算法;文献[8]改进“雕刻”规则,提出了三维点集表面重建的Alpha-shape算法。这种方法的优势在于根据设定的参数的α值大小的不同,体现出点集所具有的不同空洞信息,但是处理密度不均匀的数据时,一般需要对其进行很多的人工干预。1998年文献[9-10]先后提出了一种利用点密度估计来确定α参数的方法,避免了繁琐的人工干预,并获得更准确的Alpha形状;文献[11]提出了采用双参数Alpha-shape算法,解决了单参数在表面重建过程中精度和完整性难以兼顾的问题。
本文在前人研究的基础上,考虑到原始Alpha-shape算法其参数值的选取需要过多的人工干预和在处理不均匀点云数据的重建效果不理想这两个问题,对参数值α的选取策略进行了改进,设计出了一种依赖于近邻点平均距离的自适应步长的Alpha-shape表面重建算法。
1 三维点集的Alpha形状
文献[6]中给出了二维平面上Alpha形状的严格的数学定义,本文将二维平面上的圆推广到三维空间里的球,从而得到三维空间的Alpha形状的定义。
定义1对于任意充分小的正实数Alpha,所有包含点集S且半径为1/Alpha的闭合球的交称为点集S的Alpha包,记为positive Alpha-hull,如图1(a)所示。
定义2对于任意的负实数Alpha,所有包含点集S且半径为-1/Alpha的闭合球的补集的交集称为点集S的 Alpha包,记为 negative Alpha-hull,如图1(b)所示。
定义3对于点集S中的一点p,存在一个半径为1/Alpha闭合球,该球包含点集S中所有的点,并且点p位于球边界上,那么点p称为点集S的Alpha-极端。如果3个点p,q,r位于同一个闭合球的边界上,那么这3个点称之为Alpha-近邻。
定义4给定一个三维空间点集S和一个任意实数Alpha,那么会得到一个这样的空间多面体,该多面体的顶点是Alpha-极端,边界面是分别连接Alpha-近邻所得到三角形,这样的空间多面体称为三维空间点集S的Alpha形状。
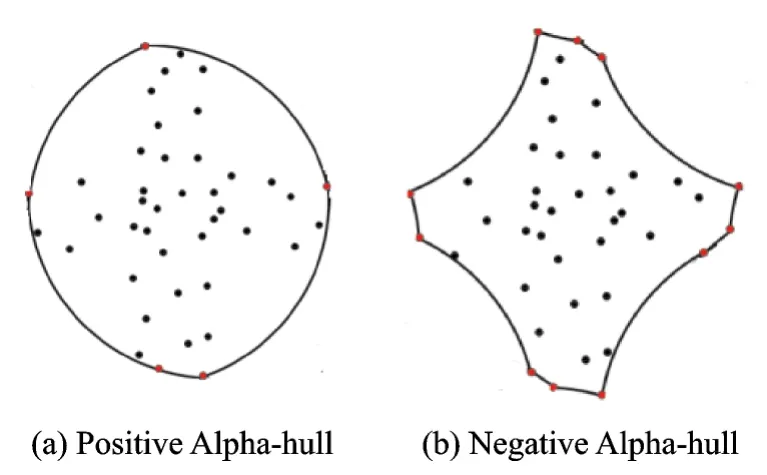
图1 Alpha包示意图Fig.1 Alpha-hull sketch map
为了便于理解后续的算法改进,本文提出了k近邻平均距离的概念。
定义5对于三维空间点集S中的任意点p,点集S中距离点p最近的k个点的距离平均值称为点p的k近邻平均距离。
2 Alpha-shape算法与分析
1994年,Edelsbrunner等提出了三维表面重建的Alpha-shape算法[8]。算法思想是以一个半径固定的小球在点集上“滚动”,半径由参数α确定,若点集不能使小球通过,那么不能使小球通过的3个点所构成的三角形就作为点集边界面,当小球“滚动”结束后可确定整个点集的表面。
2.1 算法流程
Alpha-shape算法的具体算法流程如下,其输入为n×3的三维空间点集S矩阵,每一行的3维向量代表空间中的一个点。输出为m×3的边界三角形序号集合矩阵M,其中m代表最终边界面所包含的边界三角形数量,每一行的3维向量代表一个边界三角形。设三维空间点集S={p1,p2,…,pn}。
第1步从点集S中任意选择一点p1,将与之距离小于或等于2α的点组成新的点集S1,从S1中任意选取一组点p2p3,求出过点p1p2和p3且半径为α的球的球心o和o′。
第2步遍历点集S1,依次求出其他点到球心o和o′的距离集合d和d′。如果d和d′中有1个集合的距离均大于等于半径α,则可以判断出点p1p2和p3是边缘轮廓点,三角形p1p2p3是边界三角形;如果d和d′中都有小于半径α的值时,则可以判断不是边缘轮廓点,停止遍历,转到第3步。
第3步选择S1中的下一组点按步骤1,2进行判断,直到S1中的全部点判断结束。
第4步选择S中下一个点按步骤1~3进行判断,直到S中的全部点判断结束,输出边界三角形矩阵M。
2.2 算法效果分析
以一个密度不均匀的花篮模型为例对Alpha-shape算法进行效果分析,其中花篮底部密度较大,花篮顶部“把手”部分密度较小,点集模型如图2(a)所示。当α=1时,实验效果图如图2(b)所示,由于α值过小,该算法只能计算出部分表面;加大α值,当α=2.5时,底部表面重建效果较好,但是顶部“把手”部分尚未连通,如图2(c)所示;继续修改α值直到顶部“把手”部分连通,此时α=3.1,最后的花篮模型表面重建效果图如图2(d)所示。
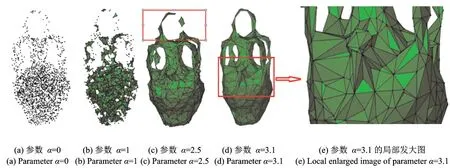
图2 Alpha-shape算法效果图Fig.2 Effect diagram of Alpha-shape algorithm
观察表面重建效果图后发现,在中间“把手”和底部交接的部分,由于过大的α值,使得表面三角形偏大,其重建效果过于粗糙,不能很好地体现物体原有的表面凹凸信息,如图2(e)所示;同时,过大的α值导致在处理密度较大的底部区域时需要遍历更多的点,从而增加了大量的程序运行时间;再者,为了得到完整的物体表面重建结果,该算法在实际重建过程中需要频繁的人工修改α参数值。综合以上几点,该算法在处理如林业测量等不均匀的数据时,有适应性不强、重建效果不理想等缺点。为了完善该算法,加大该算法的适应面,本文从α参数值的选取规则入手,提出了一种改进的Alpha-shape算法。
3 自适应步长的Alpha-shape算法
本文在文献[8]提出的Alpha-shape算法的基础上改进了α参数值的选取规则,核心思想是利用kd-tree计算每个点的k近邻平均距离,以该距离作为α参数值,采用动态的α值来进行后续的操作,称之为自适应步长的Alpha-shape算法(Variable Alpha-shape step algorithm,VAS)。
3.1 算法流程
第1步对点集S建立kd树,从点集S中任意选择一点p1,计算点集S中距离点p1最近的k个点的平均距离,记为α;将距离点p1小于2α的点组成新的点集S1,从S1中任意选取一组点p2p3,求出过点p1p2和p3且半径为α的球的球心o和o′。
第2步遍历点集S1,依次求出其他点到球心o和o′的距离集合d和d′。如果d和d′中有一个集合的距离均大于等于半径α,则可以判断出点p1p2和p3是边缘轮廓点,三角形p1p2p3是边界三角形;如果d和d′中都有小于半径α的值时,则可以判断不是边缘轮廓点,停止遍历,转到第3步。
第3步选择S1中的下一组点按步骤1,2进行判断,直到S1中的全部点判断结束。
第4步取S中下一个点按步骤1~3进行判断,直到S中的全部点判断结束。
需要说明的是:在第1步中,过点p1p2和p3且半径为α的球的球心有以下3种情况:(1)点p1p2和p3所构成的外接圆半径大于α,此时不存在过该3点的球,但是该情况不在算法流程中出现,见3.2节;(2)点p1p2和p3所构成的外接圆半径等于α,此时球心o和o′重合;(3)点p1p2和p3所构成的外接圆半径小于α,此时球心o和o′关于面p1p2p3对称。
算法中涉及点集异常处理,主要包括如下3种情况:(1)对于3个及以上的点共线的情况,所形成的边只记距离最远的2个点所形成的边;(2)对于4个及以上的点共圆的情况,所形成的边界面以多边形三角剖分为基础,避免出现边界线交叉的情况;(3)对于4个及以上的点共球的情况,所形成的边界面以多面体三角剖分为基础,避免出现边界面交叉的情况。
3.2 两种算法的效果比较
VAS算法第1步中kd-tree的k近邻查询的平均时间复杂度为O(logn),第2步求距离集合的时间复杂度是O(n),第3步遍历的时间复杂度是O(n2),第4步遍历的时间复杂度是O(n3),所以该算法总的时间复杂度为O(n3)。
对于点集密度不均匀的情况下,原始的Alpha-shape算法由于其固定的α值,在处理点集的稀疏部分时,过小的α值将不能反应点集的形状信息,过大的α值将导致算法第1步在处理点集密集区域时,所需要遍历的点数很多,直接加大了程序运行负担。而VAS算法,通过动态改变α值,在保证形状信息的前提下程序运行时间更短。同时,由于其改变α值,所以针对不均匀三维点集的表面重建效果,VAS算法更能反应原始数据的表面信息。图3是原始算法和VAS算法针对密度不均匀的花瓶点集的表面重建效果图,原始算法的表面三角形偏大,其重建效果过于“粗糙”,如图3(a)所示。而VAS算法的表面三角形较小,其表面重建效果更“细腻”,能更准确地重建出点集表面的凹凸信息,如图3(b)所示。通过图4的对比,改进后的VAS算法的表面重建效果要优于原始的Alpha-shape算法。

图3 两种算法效果对比Fig.3 Comparison of two algorithms
4 实验验证
实验针对Alpha-shape算法和VAS算法的时间效率进行对比,实验数据分为两类:计算机随机生成点集(简称为随机点集)和现实对象采集的三维点集(简称为采样点集)。
4.1 随机点集的生成
实验所用的随机点集分为球形点集和矩形点集,每类又分为均匀轮廓点集、非均匀轮廓点集、均匀内部点集和非均匀内部点集,共8组数据,每组的点数为1 000个。
球形随机点集的解析式为

轮廓点不均匀的点集分布情况为:上下距离轴线π/4区域内的点数是中间π/2区域内点数的3倍,如图4(a)所示;包含内部点的不均匀点集分布情况为:下半球区域内的点数是上半球区域内的点数的3倍,如图4(b)所示;而均匀点集是服从均匀分布的随机生成点。
矩形随机点集的解析式为
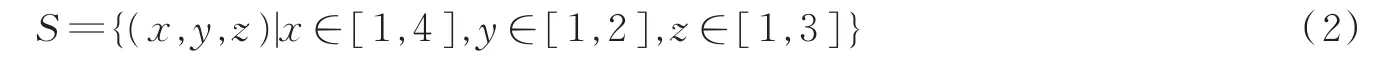
轮廓点不均匀的点集分布情况为:上、后、左三面的点数是下、前、右三面的点数的3倍,如图5(a)所示;包含内部点的不均匀点集分布情况为:上半区域内的点数是下半区域内的点数的3倍,如图5(b)所示;而均匀点集是服从均匀分布的随机生成点。
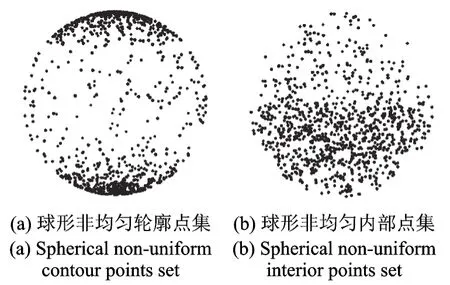
图4 球形区域不均匀随机点集Fig.4 Non-uniform random points in spherical region

图5 矩形区域不均匀随机点集Fig.5 Non-uniform random points in rectangle region
4.2 参数k的选取
关于k-近邻平均距离中参数k的确定可以参照文献[12]的确定方法。而文献[13]认为近邻点k通常在9~25之间选择一个数,即可满足实验基本要求。
由于k值的大小将直接影响局部参数α的大小,如果k值过小,相对应的局部α值将过小,此时重建并不完整,如图2(c)所示;如果k值过大,相应的局部α值将过大,此时程序的运行时间代价将会加大,同时重建效果并不理想,如图2(e)所示。本文为了确定合适的参数k,对文献[13]中提到的k值的选取范围一一进行了重建效果实验,实验数据是4.1节的球形非均匀轮廓点集、矩形非均匀轮廓点集和2.2节的花篮模型。具体程序运行时间以及重建效果对比如图6所示。从图6可以看出,直到当k≥20时,该算法针对3种不同点集的重建效果才算完整,同时由于随着k的取值变大,其对应的程序运行时间将会增长,并且其增长速度在不断增大。综上所述,本文最终选取k=20,在实际操作过程中取得了比较好的实验效果。
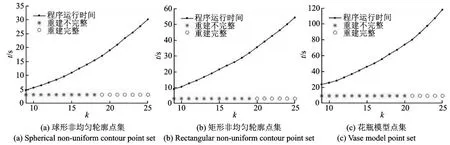
图6 不同k值的程序运行时间及重建情况Fig.6 Operation time and reconstruction of different k values
4.3 实验结果
上述算法的实验是在台式电脑上进行的,计算机配置是Intel(R)Core(TM)i7-4790 CPU@3.60 GHz处理器和4 GB内存,程序运行环境MATLAB R2016b。表1是两种算法对于不同点集的平均运行时间以及相应的α参数值对比,运行时间是重复实验20次所求的平均时间。表1中,R/S为矩形/球形;U/N为均匀/不均匀;I/O为内部点/轮廓点。 例如:RUIpts代表矩形均匀包含内部的点集。Alpha-shape算法的α参数值是满足表面重建效果的最小值,其中α参数值的改变步长为0.05;而VSA算法的α参数值是k近邻平均距离求出来的最小α值和最大α值。
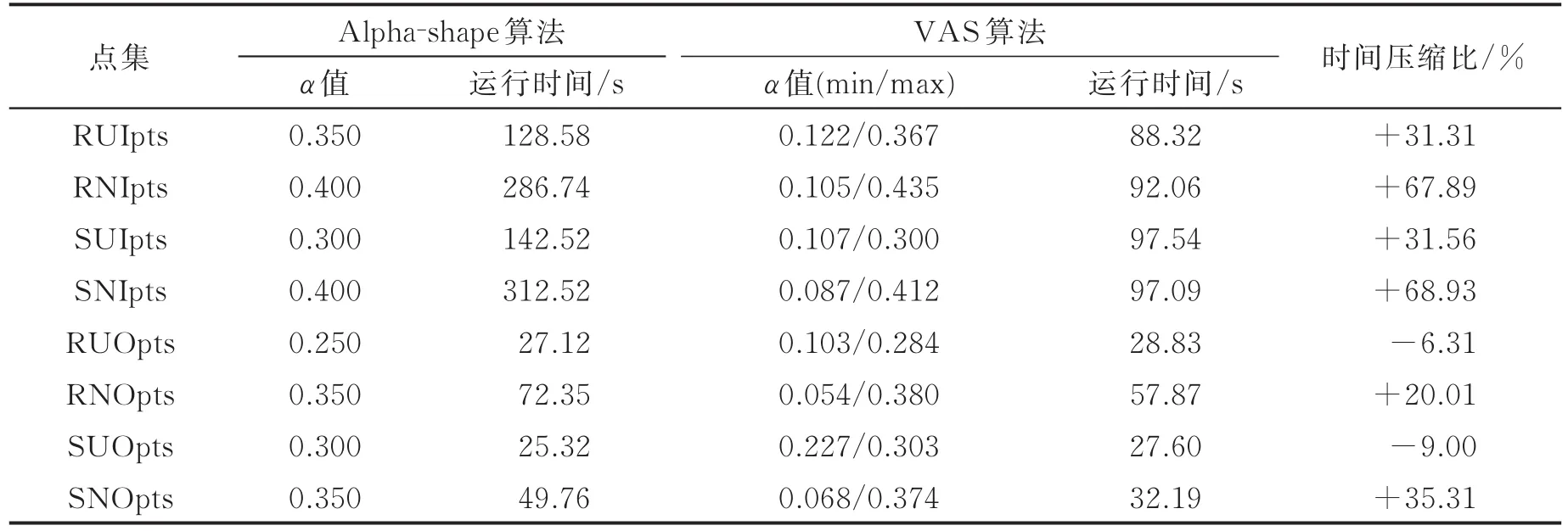
表1 两种算法针对不同的随机点集的平均运行时间Tab.1 Average operation time of two algorithms for different random point sets
算法的实验运行效果图如图7所示。

图7 随机点集的实验效果图Fig.7 Experimental effect diagram for random point sets
4.4 结果分析
从表1中的平均运行时间可以看出,本文提出的VAS算法在处理包含内部点的点集时平均运行时间能提高30%以上。特别地,在处理密度不均匀的点集时,平均运行时间能提高60%以上,这是因为在处理密度较大的区域时,采用较小的α值,减少了需要遍历点,从而提高了程序运行时间。但是在处理只有轮廓点的点集时,特别是均匀的点集,本文提出的算法在运行时间上多花费了近10%,这是因为轮廓点全是边界点,减少遍历点并不能有效地减少程序运行时间,而本文的算法在处理α值时需要消耗一定的时间,所以整体上程序的运行时间要长一些。但是对于点集密度不均匀的情况,本文提出的算法在时间效率上能提高20%以上。
4.5 激光扫描数据
本文所用的采样点集是两组三维激光扫描的数据,分别是包含树枝的不均匀的树体数据和密度比较均匀的树冠数据,两种算法的平均运行时间对比如表2所示,实验运行效果图如图8所示。实验表明,本文提出的VAS算法在实际采样点集时,针对均匀和不均匀的情况下都能提高50%以上的时间运行效率。

表2 两种算法针对采样点集的运行时间Tab.2 Operation time of two algorithms for sampling points
5 结束语
对于三维空间离散点集的表面重建问题,本文先介绍了三维空间离散点集的Alpha形状的相关概念。在分析表面重建的Alpha-shape算法的基础上,本文提出一种改进算法——VAS算法。该算法改进了原始算法针对点集密度不均匀的情况下需要过多的人工干预α参数值的缺点,采用kd-tree和k近邻平均距离来动态更新α值,这就使得该算法在处理点集密度较大的区域时也能以较少的遍历次数进行表面重建,从而为三维空间离散点集的表面重建节省了大量的时间。通过随机数据和现实三维模型采样数据等多组实验的反复验证,实验结果表明本文提出的改进算法与原始算法相比,除了轮廓点随机数据的运行时间比原始算法的时间长,其余数据的时间效率都有大幅度的提高。
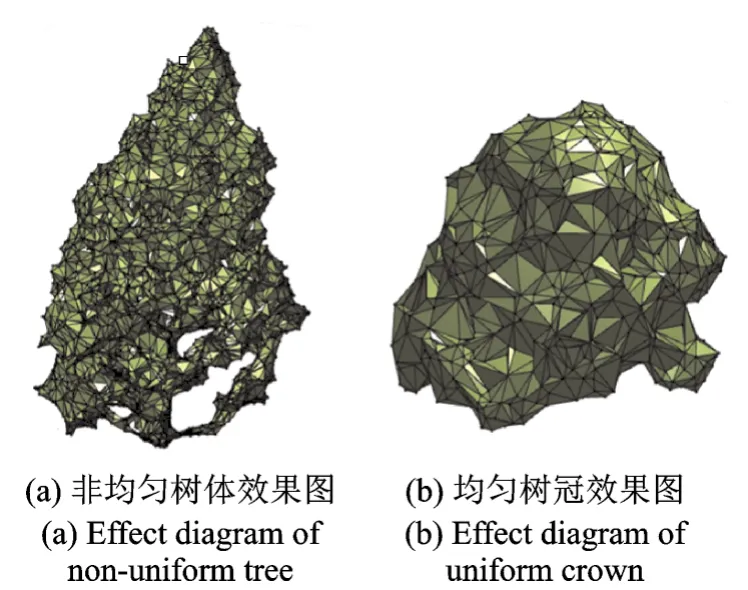
图8 采样点集的实验效果图Fig.8 Experimental effect diagram for sampling points
未来的工作之一是利用本文提出的算法把2015年家里加州大学圣地亚哥分校(University of California)Ery Arias-Castro教授等的周长计算工作[14]推广到三维形状的表面积和体积计算;把新算法的体积计算结果与文献[15-16]的结果进行比较;另一项工作是进一步改进表面重建算法效率,采用文献[17]所提出的基于密度的快速聚类方法,将点云数据进行聚类,对每一类固定其参数α值,从而缩短确定局部参数α值的时间,这样在保证重建效果的基础上可以进一步提高算法的时间效率。
