一种基于加权TOPS的宽带DOA估计新方法

陈明建 胡振彪 陈 林

（国防科技大学电子对抗学院，合肥，230037）

引 言

宽带信号由于具有抗干扰能力强、分辨率高等特点，已在雷达、声纳、医学成像等领域得到了广泛应用。宽带信号波达方向(Direction of arrival,DOA)估计一直是阵列信号处理的重要内容[1]。传统基于子空间类的空间谱估计技术，如多信号分类法（Multiple signal classification,MUSIC）[2]、旋转子空间不变法（Estimation of signal parameters via rotational invariant techniques,ESPRIT）[3-4]以及子空间拟合法[5]均假设信源为窄带信号。针对宽带信号的DOA估计主要分为两类：非相干子空间法（Incoherent signal-subspace method，ISSM）和相干子空间处理法（Coherent signal-subspace method，CSSM）[6],其中ISSM方法只有在高信噪比条件下具有较好的估计效果，且不能处理相干信源；CSSM方法在低信噪比条件下估计性能优于ISSM法，但该方法需要角度预估计和预选参考频点，DOA估计准确性易受这些先验信息影响。近些年来，学者们基于阵列信号空间稀疏特性，将稀疏重构的思想应用到DOA估计中，提出了很多基于稀疏表示与重构的DOA估计方法[7-10]，具有很好的估计精度和空间分辨能力。但这类方法的关键在于如何正确建立宽带信号稀疏模型和选择合适稀疏重构算法，算法的性能依赖于模型参数。

Yoon等[11]提出了一种投影子空间正交性测试（Test of orthogonality of projected subspaces，TOPS）算法，该算法无需角度预估计，但该方法若选择参考频点处信号子空间估计不准确，会造成谱峰搜索过程中出现伪峰。Shaw等[12]对TOPS法进行了修正，一定程度上降低了噪声对谱峰搜索影响，但伪峰问题依旧存在。Okane等[13]提出了平方TOPS方法，提高了DOA估计精度；Hayashi等[14]对平方TOPS进行加权修正，进一步改善了算法性能，避免了伪峰，但该算法复杂度较高。Yu等[15]提出了基于频域子空间正交性测试的宽带DOA估计方法，避免了TOPS方法中常见的伪峰，但该方法在低信噪比时DOA估计不准确，且对空间信源间隔相近时分辨率较差。

针对传统TOPS算法DOA估计精度不高，且易出现伪峰问题，提出了一种基于加权TOPS宽带DOA估计新方法。该方法首先通过选择最优频率点的信号子空间，同时利用信号子空间投影代替其零空间投影；然后根据导向矢量与噪声子空间的正交性，结合TOFS方法优点，对平方TOPS判定矩阵进行加权处理，得到修正后TOPS算法；最后对判断矩阵求迹运算实现宽带DOA估计。该方法无须奇异值分解，极大减少了运算量，能够有效剔除伪峰，提高DOA估计精度，且对信源来波方向相近时分辨能力更高。

1 宽带信号模型

考虑远场空间存在K个宽带信号，信号带宽均为B=[fL,fH]，以角度入射到由M元阵元组成的均匀线阵上，阵元间距d为最高频率对应半波长，则第m号阵元接收到的信号为

式中：sk(t)为第k个宽带信号，νm=(m-1)d/c，c为光速，nm(t)为零均值，方差为的复高斯白噪声。

对接收数据xm(t)做离散时间傅里叶变换，将其划分为J个子带，即表示为

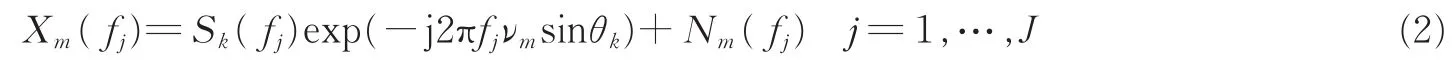
将所有阵元输出Xm(fj)写成矩阵形式为

式中A(fj,θ)表示频点fj处阵列流型矩阵，其列向量为a(fj,θk)可表示为

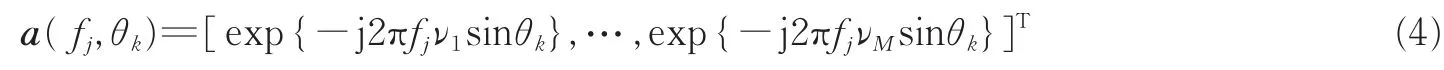
则X(fj)的协方差矩阵为

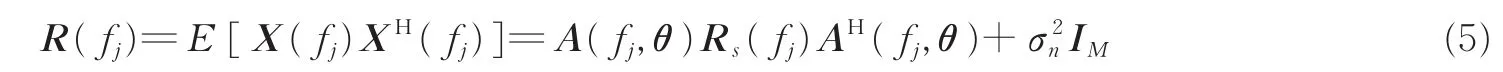
式中：Rs(fj)=E[S(fj)SH(fj)]，IM为M×M维单位矩阵。

若K个信源互不相关，则对R(fj)特征分解，可得信号子空间Fj、噪声子空间Wj分别为

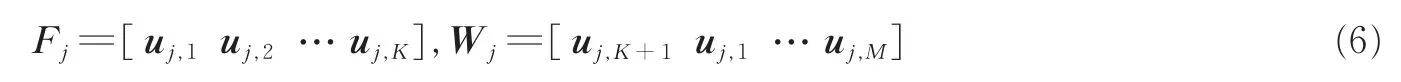
式中uj,m为R(fj)特征分解对应的特征向量，对应的特征值由大到小降序排列。

2 投影子空间正交性测试方法

2.1 TOPS算法

假定对角酉变换矩阵Φ(fi,θi)为

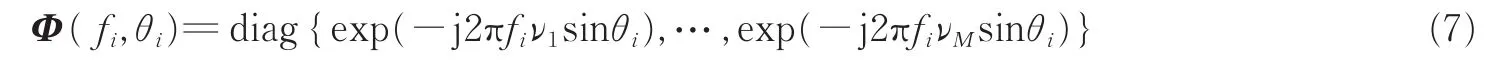
则新的阵列方向向量为

式中fk=fi+fj，sinθk=(fi/fk)sinθi+(fj/fk)sinθj。若θi=θj，则有θk=θj，即导向矢量可由频点fj变换到fk，而不改变其DOA信息。

假定Δf=fj-fi，文献[11]证明了下列两个矩阵的值域是相等，即

式中新角度依赖于θ，满足如下关系

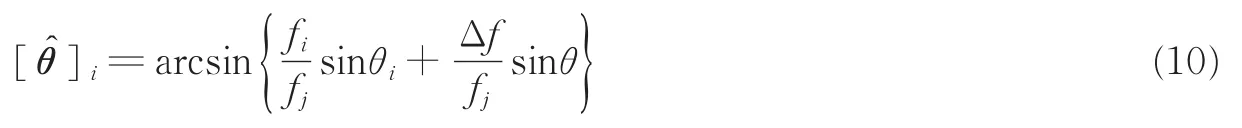
式中符号[∙]i表示矢量的第i个元素。若假定2K≤M，K+1≤J，定义M×K的矩阵为

式中θ为可能的到达角。

假定参考频点为f1，定义K× (J-1)(M-K)矩阵D(θ)为

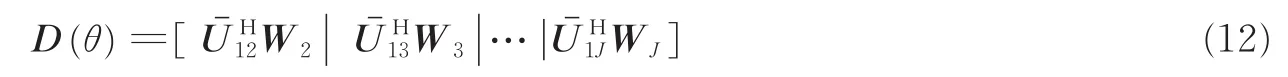
为了行文简洁a(fj,θj)简写为aj(θ)，定义aj(θ)零空间的投影矩阵为

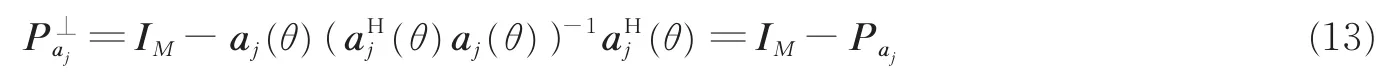
式中Paj为aj(θ)的投影矩阵。

为了减少Uj估计误差，利用修正得到Uij(θ)，即

将Uij(θ)代替重新计算矩阵D(θ)，同时为了提高 DOA 估计精度，文献[13]提出平方 TOPS方法，即

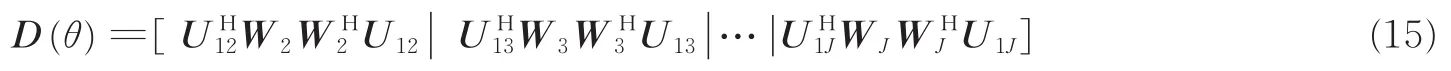
对矩阵D(θ)进行奇异值分解，由最小奇异值σmin(θ)对应的角度可得到DOA估计值，即

利用式(16)进行谱峰搜索得到DOA估计。

2.2 TOFS算法

由子空间理论可知，当假定的来波方向θ等于某个真实的信号波达方向时，满足

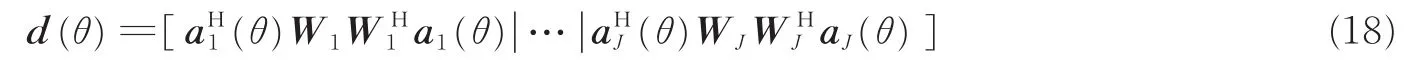
同理，TOFS算法可以根据下式估计信源DOA，即

式中‖∙‖表示对向量求ℓ2范数。

3 加权TOPS算法

3.1 信号子空间构造投影矩阵

在TOPS算法中，利用信号子空间的零空间投影矩阵以消除信号子空间F1估计误差，仍无法避免伪峰存在，且算法DOA估计精度不高。

由式(11)可知：

（1）当θ∈θ时，矩阵与信号子空间F1正交，即理想情况下某一行向量将退化为零向量，即式(16)在来波方向能够出现峰值的原因。

（2）当θ∉θ时，非正交，此时D(θ)中的部分列向量可表示为

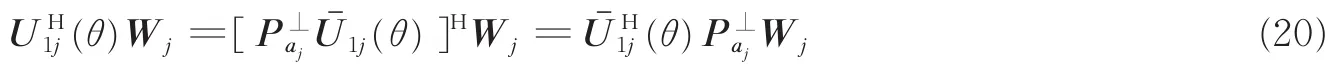
为了解决该问题，利用信号子空间投影替代其零空间投影，即

当θ∈θ，假定没有噪声，利用关系式，则

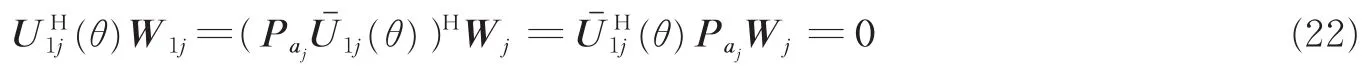
因此，利用信号子空间投影矩阵代替其零空间投影矩阵，并不影响真实信源的DOA估计，且进一步降低了噪声对空间谱估计影响，部分解决了伪峰问题。

3.2 利用TOFS加权构造矩阵

上一节讨论了基于信号子空间投影方法降低了噪声对DOA估计的影响，但仍然没有彻底解决伪峰问题。TOFS方法是根据方向矢量与噪声子空间的正交性得到构造矩阵，避免了伪峰出现，因此考虑利用TOFS加权得到修正的平方TOPS方法。

修正后的加权TOPS构造矩阵为

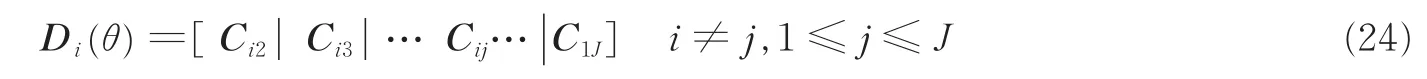
3.3 最优参考频点的选取

若假定在频带fj内信号子空间和噪声子空间对应的最小和最大特征值分别为λj,s=min{λj,1,…,λj,K}，λj,n=max{λj,K+1,…,λj,M}。定义特征值区分度为ηj=λj,s-λj,n，则最优参考频点可由式(25)求得

因此，基于最优参考频点的加权TOPS构造矩阵为

3.4 基于矩阵迹的判决函数

加权TOPS法通过D(θ)的秩缺程度估计DOA，即式(16)，等价求解如下约束优化问题

式中：rank{∙}表示矩阵秩；Θ为DOA搜索空间范围。

式(27)是个NP优化问题，传统算法通过对D(θ)的最小奇异值来判断其缺秩情况，因此需要奇异值分解，计算量较大。为了解决该问题，本文利用近似松弛的方法，式(27)可近似等价为

式中符号‖∙‖∗表示矩阵的核范数，等价于矩阵所有奇异值之和，即

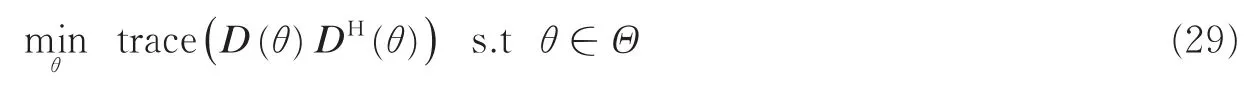
式中符号trace(A)表示矩阵A的迹。

因此加权TOPS算法可表示为

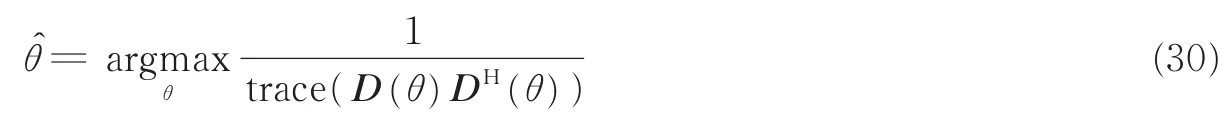
3.5 算法复杂度分析

为了便于讨论，分析TOPS法[11]、平方TOPS法[13]、WTOPS[14]、TOFS法[15]和本文方法的计算复杂度，假定阵元是为M、信源数为K、宽带分解的子带数为J、频域快拍数为N，WTOPS算法选择的频点数为J′，一般情况下满足min{J,N}＞M＞K。对于M×M维矩阵奇异值或者特征值分解的运算量为O(M3)。本文算法计算主要由以下 4个步骤决定：（1）计算协方差矩阵R(f)：O(M2NJ)；（2）对R(f)特征分解 ：O(JM3)；（3）计算判决矩阵D(θ)：O(2KM(M-K)+K2(M-K)(J-1))；（4）矩阵求迹trace(D(θ)DH(θ))：O(2K3(J-1))；而 TOPS法、平方 TOPS法、WTOPS法[14]以及 TOFS法的复杂度主要包括4个步骤，其中前两个步骤与本文算法相同，即计算协方差矩阵R(f)：O(M2NJ)；（2）对R(f)特征分解：O(JM3)，而后两个步骤分别为（3）计算判决矩阵D(θ),TOPS：O(KM(M-K)(J-1))、平方TOPS：O(2KM(M-K)+K2(M-K)(J-1))、WTOPS：O(2KM(M-K)+K2(M-K)(J-1))J′、TOFS：O(2KM(M-K));(4)对D(θ)奇异值分解，TOPS：O(K2(M-K)(J-1))、平方 TOPS：O(K3(J-1))、WTOPS：O(K3(J-1)J′)、TOFS：O(M3(J-1))。由于本文算法谱峰搜索无需奇异值分解，而是利用矩阵求迹得到谱估计，相比于其他类方法，可见本文算法在算法复杂度上有较大优势。

综上所述，本文算法计算步骤如下：

（1）对阵列接收到宽带信号数据进行分段，对每段数据进行离散傅里叶变换DFT；

（2）求得各频点处的协方差矩阵R(fj)，对其特征分解得到信号子空间Fj和噪声子空间Wj；

（4）利用信号子空间投影矩阵Paj，修正得到矩阵Uk0j(θ)；

（5）利用式(26)得到修正的TOPS法的构造矩阵D(θ)；

（6）利用式(30)进行谱峰搜索，得到K的局部极大值点，即为宽带信号的来波方向。

4 仿真实验

实验条件：均匀线阵阵元数为M=12，阵元间距为宽带信号最高频率对应的半波长。远场独立宽带信号带宽为B=200 MHz，阵列噪声矢量为复高斯白噪声。DFT点数为256，Montel-Carlo实验次数为200次。

实验1不同信噪比情形下空间谱

若3个独立远场宽带信号的到达角DOA分别为-12°，30°，35°，图1是信噪比SNR分别为5，20 dB时DOA估计的空间谱。

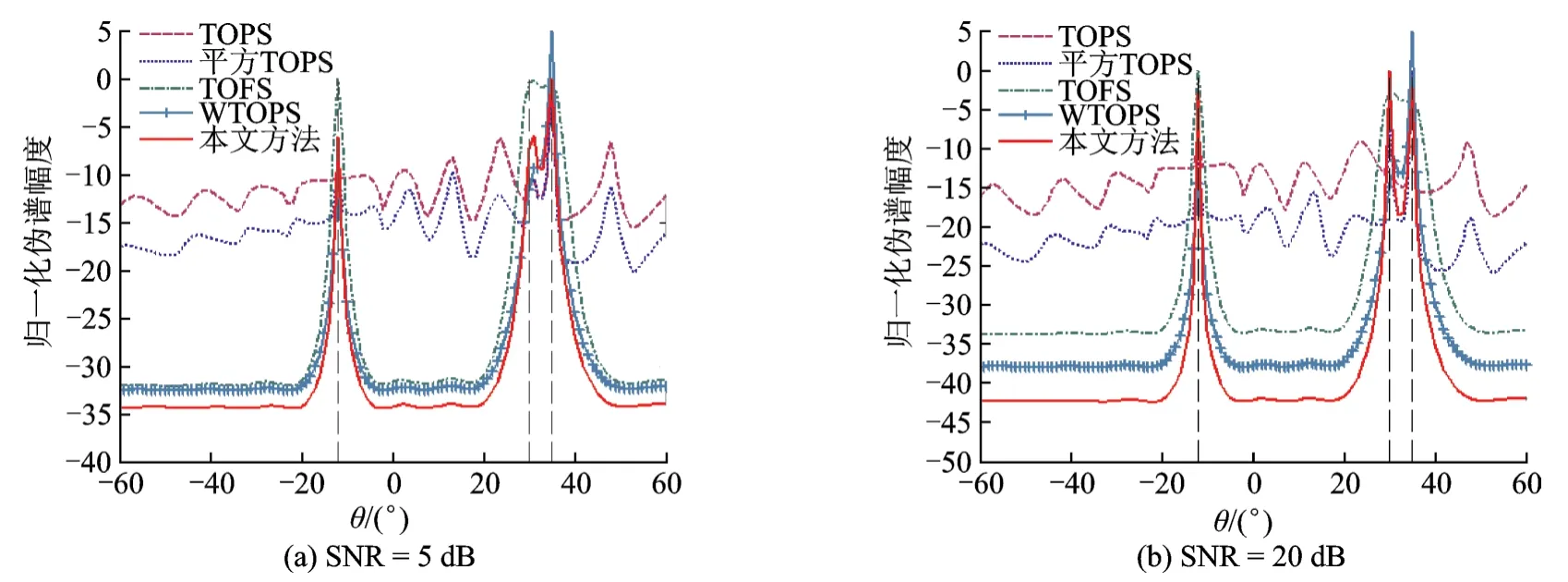
图1 不同算法空间谱比较Fig.1 Spectrum comparison between five different approaches

由图1可知，传统TOPS法、平方TOPS法由于仅仅利用某一个频点的信号子空间得到构造矩阵，若信号子空间与噪声子空间有误差（根本原因是协方差矩阵估计误差导致），则导向矢量与噪声子空间的正交性不能得到保证，即易出现多个伪峰，WTOFS由于利用导向矢量与噪声子空间的正交特性，因此有效避免了伪峰问题，但TOFS法对角度相近的信源分辨率较差，如当两个信源来波方向为30°，35°，TOFS伪谱几乎无法分辨，而WTOPS和本文方法继承了TOFS法的优点，且本文方法利用信号子空间投影修正了传统TOPS，进一步减少了噪声对谱峰搜索的影响，剔除了伪峰，对分辨角度相近的信源分辨率更好。

实验2不同信噪比情形下信号DOA估计精度与有效估计概率

考虑两个独立宽带信号源入射方位角分别为θ1=9°，14°，定义DOA估计平均均方根误差，假定真实宽带信号DOA集合为Θ，估计值集合为，若card{Θ}=（符号card{∙}表示集合的势，即集合包含元素的个数），且，，则表示为有效估计。图2为不同信噪比条件下DOA估计的均方根误差。图3为不同信噪比条件下DOA有效估计概率。

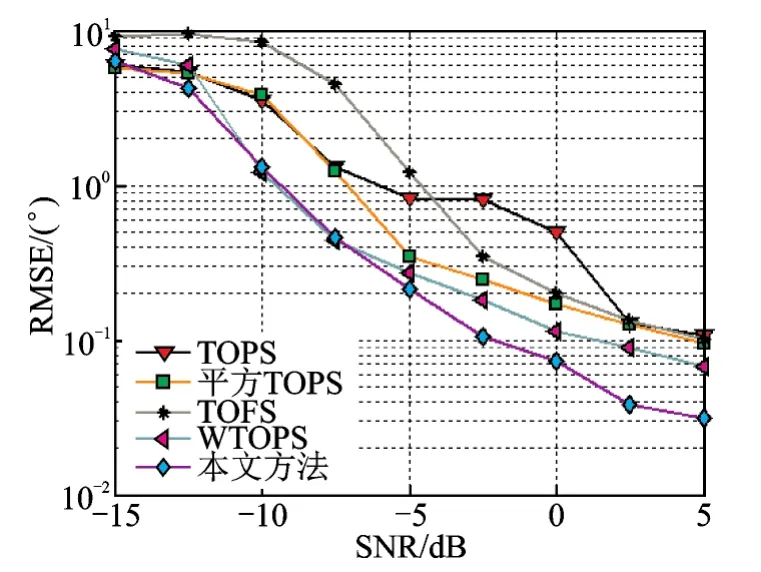
图2 不同信噪比SNR时算法均方根误差RMSEFig.2 Root mean square error(RMSE)v.s.SNR

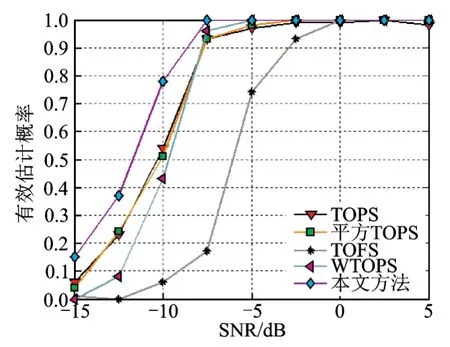
图3 不同信噪比SNR时算法有效估计概率Fig.3 Probability of effective estimate v.s.SNR

由图2可知，在SNR小于-7.5 dB时，由于噪声影响较大，对传统TOPS构造函数“平方”处理对DOA估计性能改善有限，因此平方TOPS法与TOPS法的DOA估计RMSE几乎相同；而当SNR大于-7.5 dB时，由于伪峰的存在，TOPS法表现出性能不稳定，而平方TOPS法对DOA估计精度优势逐渐体现出来；由于TOFS利用方向向量与噪声子空间正交特性，避免了伪峰，且提高了DOA估计RMSE性能，此时平方TOPS法与TOFS法DOA估计RMSE类似；在SNR大于-10 dB时，本文所提的加权TOPS法和WTOPS算法的RMSE均小于其他3类算法，这是由于这两类算法均继承了TOFS法和平方TOPS法各自的优点，提高了DOA估计精度，且本文算法性能更优，算法复杂度更低。

由图3可知，TOFS法对角度相近的信源分辨性能较差，TOPS法、平方TOPS法以及WTOPS的有效估计性能类似；相比较而言，加权TOPS法对角度相近的信源分辨性能相对最优。

实验3不同角度间隔时信号DOA估计精度与成功分辨概率

考虑两个独立宽带信号源入射方位角为θ1=10°，θ2=10°+Δθ，信噪比SNR为5 dB。假定宽带信号 DOA 的估计值分别为，若，则认为成功分辨两相近目标。图4为在不同角度间隔下DOA估计RMSE性能。图5为在不同角度间隔下目标成功分辨概率。

由图4，5可知，随着Δθ的增大，5类算法对角度相近目标分辨性能逐渐增强，WTOPS法与本文方法的性能优于其他3类算法，且本文方法的RMSE性能相对最优；当Δθ为1.5°时，其他4类方法均无法正确估计，而本文算法成功估计概率达到90%以上，即具有更高的分辨临近目标的能力。需要说明的是，在图4中TOFS、WTOPS与本文方法在角度间隔小于某一定值时，由于无法分辨相近信源，因此出现有些数据点“丢失”现象。

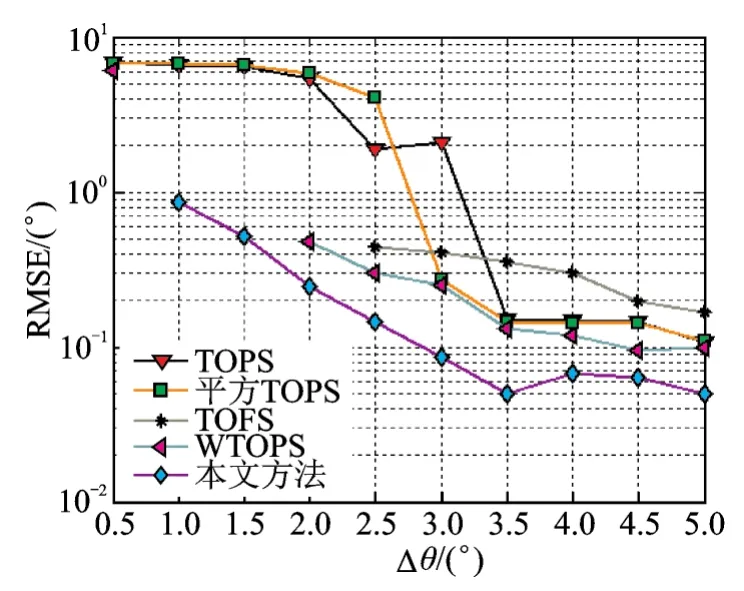
图4 不同角度间隔下算法RMSEFig.4 Root mean square error(RMSE)v.s.different angle intervals

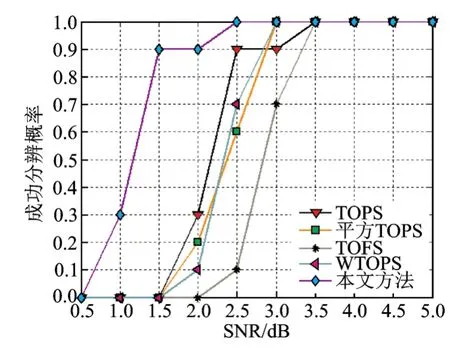
图5 不同角度间隔下算法成功分辨概率Fig.5 Probability of resolution v.s.different angle intervals

5 结束语

针对传统TOPS算法DOA估计精度较差，易出现伪峰问题，本文提出了加权TOPS宽带信号DOA估计方法，该方法继承了TOFS和平方TOPS法各自优点，且通过选取最优参考频点，利用信号子空间投影代替其零空间投影，进一步解决子空间估计误差引起的伪峰问题，然后通过矩阵求迹搜索谱峰，避免了特征值分解，减小了计算量。最后的仿真实验验证了该方法的有效性。