主成分分析在房地产数据中的应用

姜婷

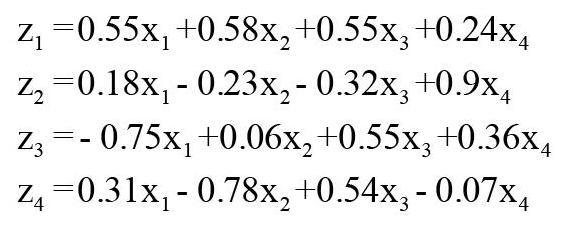
【摘要】本文利用2006年沪深股市24家房地产上市公司的年报数据，利用SAS软件来展现主成分分析在房地产数据中的应用，并得出结论，认为用主成分分析在预处理数据上发挥了重要作用，使得主成分分析与其他统计方法更好地结合应用。

【关键词】主成分分析;房地产;SAS

1引言

21世纪以来，国内的房地产行业日渐火爆，房价上涨迅速，房地产业正在逐步成为很多地区经济发展的强支柱，不仅拉动着经济的增长，也在改善人民的居住水平。但是在发展的過程中，房地产市场的泡沫不断增大，房价的虚高也增加了百姓住房的困难，使得过多资本流人到房地产业。针对这些情况，政府也实事求是地出台了各种政策，从2005年的“新国八条”到2017年的宏观调控政策，大力发展“互联网+”模式等都是为了减小百姓在住房问题上的压力。

2主成分分析基本思想

当我们在研究某个课题或项目时，为了更准确、更全面地反映所研究对象的特点及其发展规律时，我们第一反应就是寻找与其有关的因素，这样会产生两个问题：一是由于害怕丢失原始数据的重要信息，会自然地考虑很多指标，这就增加了研究过程的复杂度：二是选取的指标之间会出现多重共线性问题，就会抹杀所研究对象的内部真实特点和规律。针对上述问题，我们就会希望在定量研究中能有个两全其美的办法，既可以减少涉及的变量个数，又不会遗漏重要的信息。而主成分分析恰是研究如何通过对具有一定相关性的多个变量进行线性组合得到几个不相关的综合指标，且能解释原始数据的绝大部分信息。

变量问存在一定的相关性，通过对原始变量的相关矩阵或者协方差阵内部关系的研究，利用线性变换，将相关的原始变量转变为不相关的新的综合变量，这既保留了绝大部分的原始信息，也起到降维和简化问题的作用。

要想从研究对象错综复杂的关系中得到一些主干特点，主成分分析就恰好发挥了作用，通过这种多元统计方法，可以有效利用海量数据进行定量分析，揭示研究对象的内部信息，进一步挖掘其内在发展规律，从而能对症下药，找出实事求是的解决办法。

3实证分析

3.1样本选取与数据来源

本文采用2006年沪深股市24家房地产上市公司的年报数据，利用SAS软件研究我国房地产上市公司盈利能力与资本结构之间的关系。我们将销售净利率x1.资产净利率x2.净资产收益率x3及销售毛利率x4纳为反映上市公司盈利能力的指标，用资产负债率v来反映公司资本结构。

3.2实证结果分析

3.2.1相关性分析

先用Excel对这五个变量做一个折线图，了解各房地产上市公司资产负债率与销售净利率等其他变量的关系，发现各房地产上市公司资产负债率与销售净利率等其他变量的关系并不完全相关。

根据上市公司盈利能力四项指标之间的相关系数矩阵结果，除了销售毛利率与资产净利率之间的相关系数相对较低，约为0.17.其他指标之间的相关系数都相对比较高：销售毛利率与销售净利率相关系数约为0.45.净资产收益率与销售净利率的相关系数将近为0.67.资产净利率与销售的净利率相关系数约达到0.8.资产净利率与净资产的收益率之间的相关系数甚至高达0.9。这说明四个指标之间存在显著相关性，指标之间具有多重共线性，所以采用主成分分析法对四个指标进行降维。

3.2.2主成分分析

根据相关系数矩阵计算出的所有特征值、相邻两个特征值之间的差值、每个特征值对应的方差贡献率以及累积贡献率。特征值越大那就说明它所对应的主成分变量包含信息就越多。第一个至第四个主成分贡献率分别约为67.12%、25.20%、6.09%、1.59%，前两个主成分就包含了原来四个指标92.32%的信息，所以表明可以提取前两个主成分。

然后根据全部特征值对应的特征向量，就得到各主成分的数理关系式，即：

各标准化指标前面的系数绝对值越大，说明该主成分受该指标的影响就越大。前三个标准化指标对第一主成分大小的影响差不多，都在0.55上下波动：决定第二主成分z，大小主要为销售毛利率，其系数高达0.9：影响第三主成分大小主要为销售净利率和净资产收益率，系数分别约为-0.75、0.55.二者对第三主成分大小的作用相反：决定第四主成分大小主要为资产净利率和净资产收益率，系数分别约为-0.78、0.54.二者对第四主成分大小的作用也相反。

由此得出：第一个主成分与前三个指标关系都比较大，说明它主要涵盖前三个指标的信息，第一个主成分可以称之为“公司资产的获利能力”;而第二个主成分主要涵盖了第四个指标的信息，可以称之为“公司的经营能力”。

3.2.3综合评价

由于主成分z1和z2从不同角度反映了这24家上市公司的盈利能力，所以可以考虑按z1和z2的加权平均值进行排序，然后了解哪一家上市公司的盈利能力最好。根据结果显示：中粮地产的三项指标均名列第一，而高新发展综合排名倒数第一。

4总结

在研究房地产信息时会有大量的数据，这些数据并不都是有用的，如果在研究某些自变量对某一个因变量影响程度时，把自变量都纳入研究范畴，就会出现大量信息重叠情况，无法准确反映原始数据的重要信息。用较少数量的特征对样本指标进行降维就特别重要。所以在分析数据时，主成分分析占有重要的地位。