互联网指数对不良贷款率的实证分析

潘宇翔

【摘要】互联网快速发展的宏观环境下，联系互联网金融的概念、特征、发展状况以及当前商业银行不良贷款成因、现状，理论分析两者之间的关系和影响途径，然后利用多元线性回归模型实证分析互联网指数对银行不良贷款率造成的影响。通过多元线性回归方法着重分析互联网金融与上市商业银行的因果关系，得到互联网金融的发展与上市商业银行不良贷款之间负的相关关系，即互联网金融的发展可以降低商业银行的不良贷款率。

【关键词】互联网金融;商业银行不良贷款率;多元线性回归

一、理论假设和模型设定

根据理论分析，本文提出假设：（1）互联网发展与上市商业银行不良贷款率之间存在相关关系：（2）互联网发展与上市商业银行不良贷款率之间存在线性关系。

本文的研究方法是以上市商业银行宁波银行为样本，以2011Q1-2016Q3各季度的不良贷款率为因变量，以互联网指数、权益乘数、总资产周转率、存贷比作为自变量，推导建立回归模型。由此，本文建立关于商业银行不良贷款率的多元线性回归模型：

二、估计结果和分析

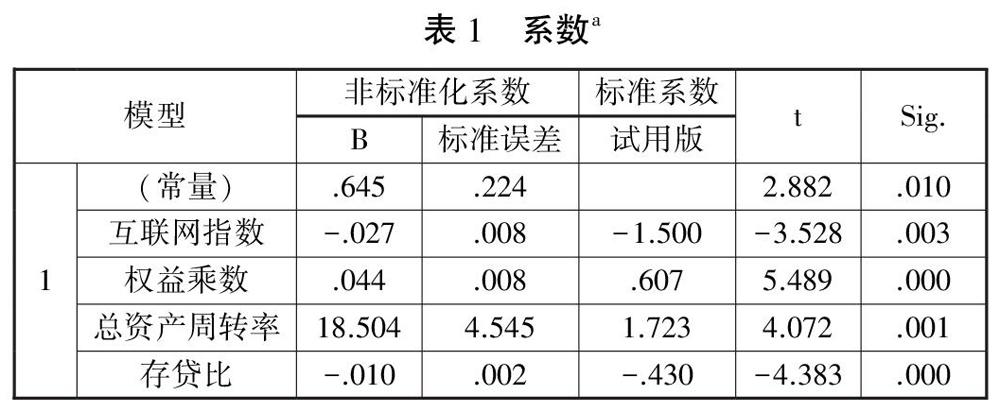
将搜集的宁波银行各季度的时间序列数据带人公式中，利用sPss20.0软件估计模型参数并进行检验。所选择的变量中未出现被移去的变量，说明该模型的拟合效果佳。

此结果的多元相关系数（R）为0.948.判定系数（R平方）为O，899.说明选取的自变量对因变量的解释度为89.9%。调整后R平方为0.870.说明其拟合程度还是可以接受的。这些值（除了随机误差的估计值）都是越大表明模型的效果越好，该模型效果良好。对于本文的多元线性回归模型可解释程度较高。

方差分析表表明了方差分析的结果。F值为89.678.其显著性概率值小于0.01.说明回归方程拟合效果很好，所以结果是放弃虚无假设，即因变量与自变量之间存在回归关系。表明不良贷款率与存贷比、互联网指数、总资产周转率、权益乘数、ROE整体间有明显回归关系存在，该模型有显著的统计意义。

最后的t检验结果中，常数项为0.645.其显著性O，010

“互联网指数”自变量的回归系数为0.027.其显著性0.003

“权益乘数”自变量的回归系数为0.044.其显著性0.044

本模型的拟合结果为：

经过上述多元回归模型的分析可知：互联网金融深化所带来的影响能在一定程度上减少商业银行不良贷款率。互联网指数的发展会降低低商业银行的不良贷款率。

三、结论和启示

本文开篇联系实际背景，从当今经济环境下重新认识了互联网金融和不良贷款。我们得出结论：存款业务方面，货币基金等互联网理财产品的兴起带给商业银行更多的是结构上的冲击，即银行存款业务中活期存款比例会不断受到定期存款额上升所引起的挤压现象。贷款业务方面，伴随着商业银行总贷款额度的锐减，则其不良贷款也具有不断下降倾向。中间业务方面，随着商业银行对中间业务规模的侧重，银行或将适度缩减贷款业务，进而一定程度上降低银行贷款总额，带来银行不良贷款率的降低。

（一）积极加强互联网金融风险管理

互联网金融带来了大数据时代，大数据利用的核心在于对未知进行预测，银行则可以充分结合大数据的应用来加强自身的贷款风险管理。银行应综合分析关于客户、资产组合的表现、金融经济形势等数据，用以改善风险计量模型的准确性，时效性和前瞻性，这对有效降低银行不良贷款率也是大有裨益的。

（二）精准营销下的安全贷款

互联网金融带来的精准营销可以在单个客户的基础上实现。銀行通过跟踪客户在网站上的点击行为，及时更新客户偏好和可信度水平并加以预测，使点对点的实时营销成为可能。