基于初始运行阶段Galileo PPP国际时间传递*
2019-06-14欧阳明俊杨旭海孙保琪葛玉龙
欧阳明俊,杨旭海,孙保琪,葛玉龙
(1.中国科学院 国家授时中心,西安 710600;2.中国科学院 精密导航定位与定时技术重点实验室,西安 710600;3.中国科学院大学,北京 100049;4.中国科学院大学 天文与空间科学学院,北京 101048)
0 引言
精密单点定位技术(precise point position,PPP)是1997年由美国喷气推进实验室J.F.Zumberge等人提出的[1]。该技术使用单台接收机采集的双频码伪距和载波相位观测值,以及IGS(International GNSS Service)提供的精密卫星轨道和精密钟差产品,采用非差模型进行未知参数的解算,其定位精度在水平方向可以达到1 cm,高程方向可以达到2 cm[1]。2006年,CCTF(Consultative Committee for Time and Frequency)建议增加载波相位时间传递链路,以进行综合原子时的归算。2009年开始,GPS PPP成为国际原子时(TAI)例行时间传递技术[2]。截至2017年2月,根据国际权度局(Bureau International des Poids et Mesures,BIPM)的T公报,全球有76个时间实验室参与国际时间比对,其中有28个时间实验室采用了GPS PPP的方法,有10个实验室采用了卫星双向时间传递与PPP结合的方法[3]。
当前国际时间比对链路中,只使用到了GPS和GLONASS系统的观测值[3]。当前基于载波相位时间传递的研究,也主要基于GPS系统开展。加拿大自然资源部(Natural Resource Canada)开发的NRcan-PPP软件[4],被BIPM时间传递部门用于TAI的试算。2004—2006年,BIPM的江志恒博士和G.Petit使用GPS PPP方法得到亚纳秒量级的时间传递精度,并且指出GPS PPP用于时间传递的短期稳定度优于TWSTFT(two-way satellite time transfer)[5]。2014年中国科学院国家授时中心广伟等进行了BDS PPP实验得出了BDS PPP时间传递短稳可以达到1×10-13/960 s,1×10-14/d[6]。2017年国家授时中心张立等对多系统产品应用于GPS PPP时间传递进行了比对[7]。
随着Galileo,BDS等新兴导航系统的蓬勃发展,利用GNSS多系统PPP方法时间传递,将有助于提高UTC/TAI计算的可靠性和准确度。Galileo系统于2016年12月15日正式对外宣布提供初始化运行服务(initial service),论文利用部分外接高精度原子钟的GNSS站点,试验探索基于初始运行阶段Galileo系统,进行PPP国际时间传递的策略与可能达到的效果,并从未知参数设置、分析中心产品、精密钟差采样间隔、频点选取等方面,对不同的解算策略进行了分析比较。
1 数据与方法
基于试验的目的,试验选取了部分国际时间比对链路,采用PPP方法进行解算,本节将介绍具体选取的数据与解算策略。
1.1 PPP方法原理
码伪距与载波相位观测方程如下所示:
(1)
(2)

PPP技术自从诞生以来,发展了多种数学模型,比较有代表性的数学模型包括传统模型,非差非组合模型,UofC模型,消模糊度模型。传统模型也就是消电离层组合,由于电离层误差在接近地平线方向最大可以达到100 m以上,目前的电离层模型均不能对其精确改正,消电离层组合为在两个频率码伪距观测值,载波相位观测值之间形成观测方程,能够有效消除消去电离层一阶项的影响,故消电离层组合得到了广泛的应用。
消电离层组合计算公式如下:
(3)
(4)
式(3)和式(4)中,PIF码代表伪距消电离层组合,ΦIF代表载波相位消电离层组合。
1.2 PPP时间传递原理
使用PPP方法进行时间传递,先使用双频码伪距和载波相位观测值以及精密产品,解算测站时钟与参考时间尺度IGST的偏差,之后两站作差运算得出时间传递结果。
在使用PPP进行时间传递时,各站点接收机外接对应的原子钟,然后使用精密轨道和精密钟差产品,利用单台GNSS接收机观测值进行PPP解算,获得本地时钟Tclk,a,Tclk,b与公共参考时间(TIGST)之间的差值,再对两个测站解得的钟差进行差分运算得到两地原子钟之间的时间偏差,得到时间传递结果。图 1为PPP时间传递原理图,计算方程具体如下:
Tclk,a-Tclk,b=[(Tclk,a-TIGST)-(Tclk,b-TIGST)]。
(5)

图1 PPP时间传递原理图
1.3 观测数据及精密产品
在使用PPP方法进行高精度时间传递时,各站点的接收机需要外接原子钟,以维持高精度且稳定的频率源。根据具有Galileo/GPS跟踪能力和外接高精度时间参考两个条件,从IGS跟踪网和TAI国际时间传递网选取7个GNSS跟踪站进行试验,除PT11站点不是IGS MGEX(multi-GNSS experiment)站,其余6个均为MGEX站点。其中PT11,BRUX,ROAP,DLF1,USN8为位于时间实验室站点。试验数据弧段从2016年12月15日开始,到2017年5月1日结束共138 d,观测数据的采样间隔为30 s。
图 2是本次试验选取站点分布图。在国际时间比对链路时间实验室站点中,PT11站点位于德国联邦物理技术研究所(PTB),也是当前国际时间比对链路中心节点。
图2 试验选取站点分布图
GBM是IGS MGEX分析中心GFZ提供的包含有Galileo系统的多系统产品,COM是IGS MGEX分析中心CODE提供的包含有Galileo系统的多系统产品。试验选取的站点所用接收机、天线配置以及外接原子钟,详细情况如表1所示。

表1 选取的站点具体配置情况
1.4 解算策略
本次试验使用中国科学院国家授时中心iGMAS分析中心自主改编的Bernese 5.2软件(可解算四系统),分别对Galileo系统和GPS系统进行PPP解算。参数估计采用加权最小二乘,未知参数包括测站坐标、对流层天顶延迟、接收机钟差、载波相位模糊度4类。解算的基本策略设置如表2所示。

表2 PPP 时间传递解算基本策略
为进一步试验未知参数设置、分析中心产品、精密钟差采样间隔、频点选取等方面,不同解算策略对Galileo PPP时间传递的影响。本次试验选取了表3中所列7种策略进行比对分析。

表3 7种策略的选取情况
1.5 评价方法
TAIPPP是BIPM为计算国际原子时而采用PPP技术解算的各时间实验室钟差,使用时延小于3 d的IGS快速产品IGR。BIPM解算TAIPPP使用的软件是由加拿大自然资源部开发的NRCan-PPP软件,本文则使用中国科学院国家授时中心iGMAS分析中心自主改编的Bernese 5.2软件(可处理四系统)。另外两种软件使用的解算策略也有所不同,部分解算策略比较如表4所示。
从表4可以看出,两个软件处理策略具有较大的差异,因此,验证Benrese 5.2软件在PPP数据处理能够达到的精度,目的是比较验证在同一条链路中,使用相同数据,相同产品的条件下,不同软件以及不同解算策略对时间传递结果的影响,也为后文能够以该软件,该策略做时间传递试验提供可信基准。
本次试验所用软件和策略,用于评估Galileo PPP时间传递的可行性,在2017年IGS Workshop 所做的报告《BeiDou and Galileo Carrier-Phase Time Transfer toward TAI Computation International GNSS Service》已经得到验证[8]。该报告中,采用Bernese 5.2软件,使用与BIPM相同的数据和产品,比较GPS PPP策略选择和BIPM公布的月结果。该试验中从MGEX站点中选择了6个站,所有6个站为位于参与国际原子时时间比对的时间实验室,数据选取的时段是从2015年1月到2017年5月。试验得到结论,采用Bernese 5.2软件,GPS PPP方法时间传递采用表3中策略1,这也是本次Galileo PPP采用的基本策略,得到的时间链路单天解算结果,其与BIPM TAIPPP月公布结果STD (Standard Deviation) 在0.1 ns左右,意味着采用该软件与该策略,作为Galileo PPP单天时间传递评估标准是可行的。
以Galileo PPP计算得到时间传递链路钟差序列与GPS PPP结果作差的统计STD,来衡量Galileo PPP时间传递能够达到的效果。具体计算公式如下:
(6)
式(6)中,tGPS_PPP(i)表示GPS PPP其138 d解算得到钟差时间序列,tGalileo_PPP(i)表示Galileo PPP整体138 d钟差时间序列,μ表示138 d里GPS PPP减去Galileo PPP时间序列均值,N为时间序列采样点个数。
2 结果与分析
本次试验从未知参数设置、分析中心产品、精密钟差采样间隔、频点选取等方面所选取的7种策略均采用GPS系统,GBM产品,钟差采样率为30 s,以及L1/L2频点的策略,也就是表3中策略1,为参考作差进行比对统计。从图3中7种策略STD统计结果可以看出:除了个别链路,个别策略作差时间序列STD统计结果大于0.6 ns,总体在0.2~0.6 ns之间。
从图3中统计结果可以看出,固定坐标,固定对流层策略Galileo PPP与GPS PPP作差得到的统计STD,所有链路均有不同程度减小,说明固定参数对Galileo PPP 解算有靠近作用;采用GBM产品或者COM产品,所有试验链路统计STD差异小于0.1 ns,说明采用不同的多系统产品,Galileo PPP时间传递几乎没有差异;而采用300 s采样间隔钟差,以及采用E1/E5b频点数据解算,这两种策略相对于基本策略,不同链路统计STD差异不同,无明显趋势,但各策略统计量级差均在0.3 ns以内。
表5为采用Galileo PPP表3中策略1,也就是使用Galileo系统、采用GBM产品、30 s钟差、E1/E5a两个频点观测数据进行解算,以GPS PPP为参考作差统计结果。从表中可以看出,STD均在0.2~0.6 ns之间。RMS(root mean square)值统计差异较大,原因在于本文只强调分析时间传递的稳定度,未对设备时延等系统误差进行标校。

表5 策略1 Galileo PPP减去GPS PPP统计结果 ns
图4为使用表3中的策略1,6条时间比对链路Galileo PPP解算时差结果与GPS PPP时差结果作差得到的时差序列图。 部分链路比对结果出现缺失是由于观测数据的缺失或数据质量较差导致解算失败。从链路比较结果可以看出,在138 d作差时差序列图中,GPS PPP方法相较于Galileo PPP方法,其幅度在上下2 ns之间,意味着解算效果表现较为稳定。
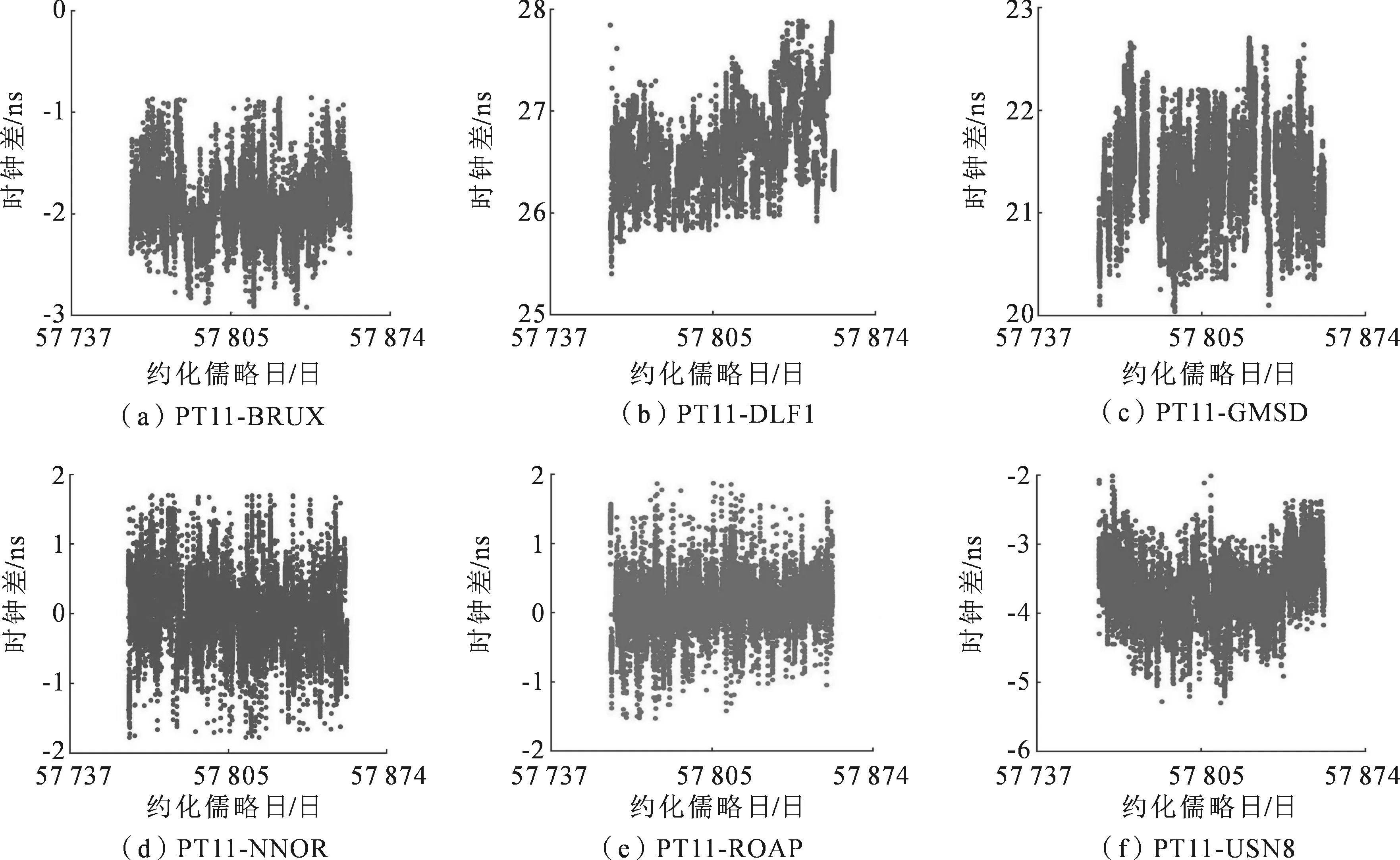
图4 策略1 Galileo PPP减去GPS PPP 时间链路结果
3 结语
本文利用多系统精密轨道钟差产品,选取Galileo系统宣布初始化运行后,连续138 d观测数据,采用PPP方法进行时间传递试验,探索Galileo PPP时间传递效果。从未知参数设置、分析中心产品、精密钟差采样间隔、频点选取等方面,对不同解算策略进行了分析比较。试验结果表明,当前Galileo卫星系统尚未全面建成的情况下,采用文中所示7种策略,以GPS PPP方法为参考,与其作差并进行统计,6条时间比对链路的统计STD均在0.2~0.6 ns之间。此结果可为Galileo系统远程时间传递,UTC/TAI时间比对等提供一定参考。
致谢:感谢IGS MGEX提供的多系统产品和观测数据;感谢PTB提供包含有Galileo系统的观测数据;感谢iGMAS提供的资助。
