课本习题深度教学的方向和策略

(衢州第二中学,浙江 衢州 324000)

《基础教育课程改革纲要(试行)》在论及教育课程改革的具体目标时指出：改革课程实施过于强调接受学习、死记硬背、机械的现状，倡导学习主动参与，乐于探究，勤于动手，培养学生收集和处理信息的能力，获取新知识的能力，分析和解决问题的能力以及交流与合作的能力.《普通高中数学课程标准(2017年版)》指出：数学探究活动是运用数学知识解决数学问题的一类综合实践活动，也是高中阶段数学课程的重要内容.自主学习及探究活动是围绕某个具体的数学问题，开展自主探究、合作探究，并最终解决问题的过程，是有效学习的重要途径之一.

下面笔者以人教版《数学(选修4-5)》第36页第6题的基本不等式为例，引导学生进行了一系列探究.

题目已知x+2y=1，求x2+y2的最小值.

本题看似简单，但内涵丰富，在教学和学习活动中不能仅满足于问题的解决，而应促使学生进行解法探究，包括条件结论互换等探究，进一步深化解题.

1 逆向探究：条件与结论的互换

变式1已知x2+y2=1,求x+2y的最大值.

先对问题进行逆向探究.此题难度虽适中，但可以提高学生学习的兴趣.

解法1(柯西不等式)由

(x+2y)2≤(12+22)(x2+y2)=5,

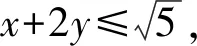
此解法关键在于结合柯西不等式的模型，找到相应的两组数.

解法2(整体代入)令x+2y=t,则x=t-2y,代入x2+y2=1得

(t-2y)2+y2=1,

即

5y2-4ty+t2-1=0，

利用y有解可得

Δ=16t2-20(t2-1)≥0,

从而

t2≤5,

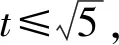
此法的核心思想是利用二次函数有解.

解法3(三角换元)令x=cosθ,y=sinθ,则

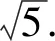
此解法正“巧遇”三角函数“sin2θ+cos2θ=1”这一特殊知识，可以激发学生思考：今后遇到类似这样的问题，是否也可采用这样的解题方法呢？

根据以上的“热身”初探，为进一步探究作好了准备，下面开始进一步探究.

2 “升元”探究：将二元变成三元

“升元”是数学探究的重要途径之一，也是激发学生求知欲的一种表现形式，更是数学思维水平提高的必走之路，可以提高学生分析问题和解决问题的能力.

变式2已知x2+y2+z2=1,求x+2y+3z的最大值.

解法1(柯西不等式)由

(x+2y+3z)2≤(12+22+33)(x2+y2+z2)=14,

易得

此方法学生容易想到，关键是要配凑好相应的数字，使其满足柯西不等式.这样的解决方法可以增强学生的自信心，很有必要.除此之外，还可以提出其他解法吗？通过认真辨析所求式子的特点，容易引起学生的思考：是否可以用三角换元的方法呢？

解法2(三角换元)x2+y2=1-z2,令z=sinα,x=cosθcosα,y=sinθcosα,则

x+2y+3z=cosθcosα+2sinθcosα+3sinα=

此解法让学生进一步体会到了三角换元的有用性.

此题可用整体代入法吗？显然不易.那么此类问题还有什么好的解法吗？如果题目的条件再变化，那该如何求解呢？

3 “深入”研究，问题提升

通过变换要求的目标进行探究，是巩固所取得探究成果的一个重要方法.观察该题，可以发现用柯西不等式的方法显然不易，三角换元的方法可行.除此之外还有其他好的解法吗？通过观察式子易知可巧妙利用基本不等式a2+b2≥2ab进一步求解，从而激发学生的探求欲望.

解因为

x2+y2+z2=x2+ty2+(1-t)y2+mz2+(1-m)z2≥

所以

解得

于是

即

该解法的核心是怎么进行合理分配，特别是x2，y2和z2的分配.采取待定系数法可有效解决.通过此变式既进一步挖掘了知识的深度，又增加了新的解题方法.

4 “多规”合一，深度挖掘

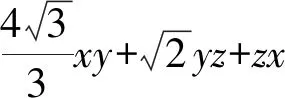
将变式3的部分数字进行如上变化，学生看到后容易蠢蠢欲动，觉得这两个问题不是差不多吗，应该容易解决.部分学生会“自傲”地急于动手，然而动手后发现：数学如此有趣，一个数字的不同，差别却是十万八千里！怎么办呢？

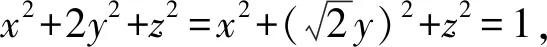
结合表达式可以发现x,y的地位一样，因此可采用如下解法：

解法1(基本不等式)

x2+y2+z2=

结合目标所求，可得

解得

于是

即

这样的探求有一个非常重要的条件：x,y互换后题目不变.此类问题是数学领域常见的一种表现形式，教师可引导学生进一步探究，尝试三角换元的方法.

解法2(三角换元)因为x2+y2=1-z2,令z=cosθ,x=sinθcosβ,y=sinθsinβ,所以

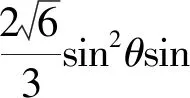
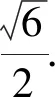
对于形如x2+y2=1-z2的式子，三角换元是不可缺少的一种解题方法，应引起广大师生的高度重视.此题还有其他解法吗？遨游数学的海洋，发挥自己的想象，可以不断推出新的思路，引发大家的探究欲望.

解法3(待定系数)因为

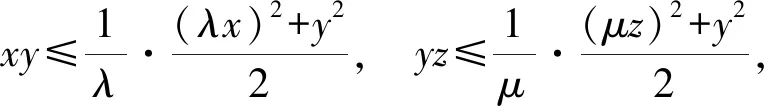
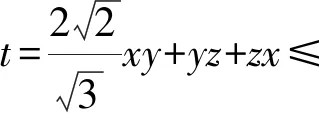
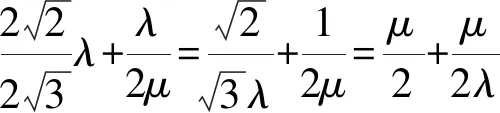
解法4(“1”的整体代换)

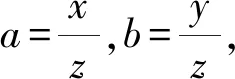
从而

解得

以上的探究过程，源于课本，又高于课本.通过对问题的不断变式，不断探究出新的解题方法，使得学生经历“问题—变式—转化—探究—再创造”的过程.一个点连成一条线，一个问题的解决涵盖了不同的知识点，使得探究意犹未尽.正如托尔斯泰说：成功的教学所需要的不是强制，而是激发学生的兴趣.心理学研究表明，学生的学习兴趣对学习效果能产生很大影响，学生学习兴趣浓厚、情绪高涨，他就会深入地、兴致勃勃地学习相关方面的知识，并且广泛地涉猎与之有关联的知识，遇到困难时会表现出顽强的钻研精神.本文通过问题的不断变式，激发了学生的求知欲，不失为一种很好的学习途径.