着眼数学建模 提升几何素养——记一节“K字模型的应用”复习课

(尚志中学,浙江 宁波 315202)

1 问题的提出

在一次八年级的课堂教学中，有这样一道题目.

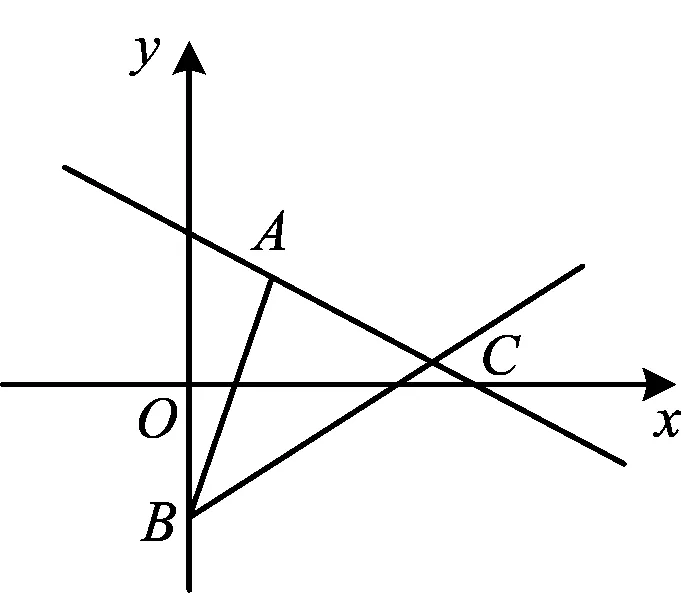
图1

学生乍看之后一脸迷茫，全班共有45位学生，个个无从下手.事后想想，八年级的学生平时学的都是单课的知识，复习也大多是以单纯的讲题为主，难以创造性地解出此题.抓住这个契机，笔者设计了以下这节复习课.

2 基本模型的建立

问题1如图2，已知AB⊥BD于点B，CD⊥BD于点D，O是BD上一点，且AO=OC，AO⊥OC，你能得出哪些结论？

分析学生易得出△ABO≌△ODC，△AOC是等腰直角三角形等结论.

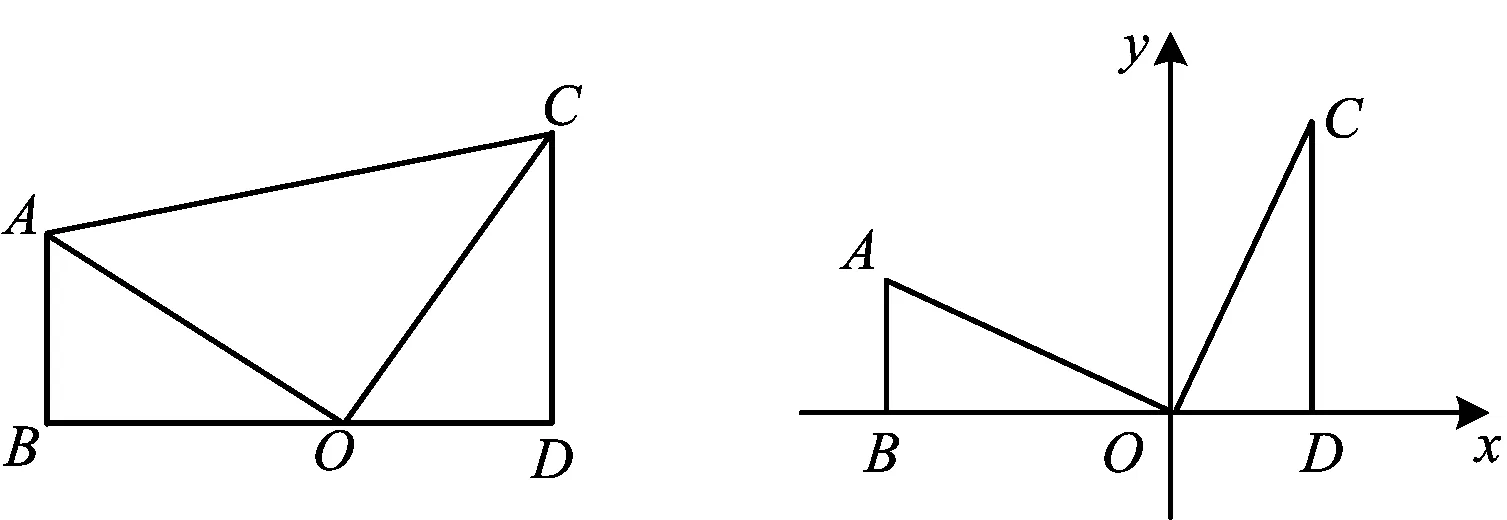
图2图3

我们把这个形状称为K字型，并进一步将其纳入直角坐标系.

问题2如图3，在图2的基础上，以O为原点、BD所在直线为x轴建立平面直角坐标系，点C(1，2)，求点A的坐标.

分析根据问题1的结论，易得A(-2，1).

再设计两个问题，让学生初步学会构造K字型.

问题3在平面直角坐标系xOy中，点C(1，2)，若△AOC是以OC为直角边的等腰直角三角形，求点A的坐标.

分析需要分类讨论.

1)以O为直角顶点.

如图4，构造K字型后，易得A(2，-1).

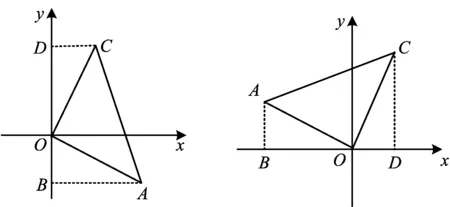
图4图5

如图5，构造K字型后，易得A(-2，1).

2)以C为直角顶点.

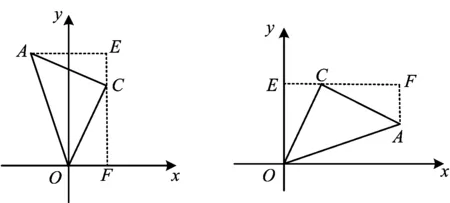
图6图7

如图6，构造K字型后，可得OF=CE=1，CF=AE=2，则点A的坐标是(-1，3).

如图7，构造K字型后，可得OE=CF=2，CE=AF=1，则点A的坐标是(3，1).

问题4在平面直角坐标系xOy中，点C(2，1)，若△AOC是以OC为斜边的等腰直角三角形，求点A的坐标.

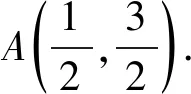
图8图9

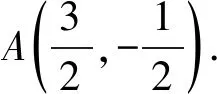
总结无论OC为直角边还是斜边，先过直角顶点构造K字型，再利用三角形全等得到两组相等的线段，可求出点A的坐标.

设计意图由于八年级学生学习过特殊三角形，对于不在平面直角坐标系的K字型比较熟悉，因此由此引入建立平面直角坐标系，循序渐进.以OC为直角边和OC为斜边画出等腰直角三角形是学生学习的难点，此时教师要给学生足够的时间，让学生自己画出图形，再引导学生构造K字型去解决问题.

3 基本模型的巩固

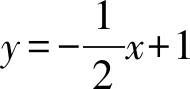
1)求直线CD的解析式.

2)在第一象限内，是否存在点F，使以E，O，F为顶点的三角形为等腰直角三角形？若存在，请求出点F的坐标；若不存在，请说明理由.

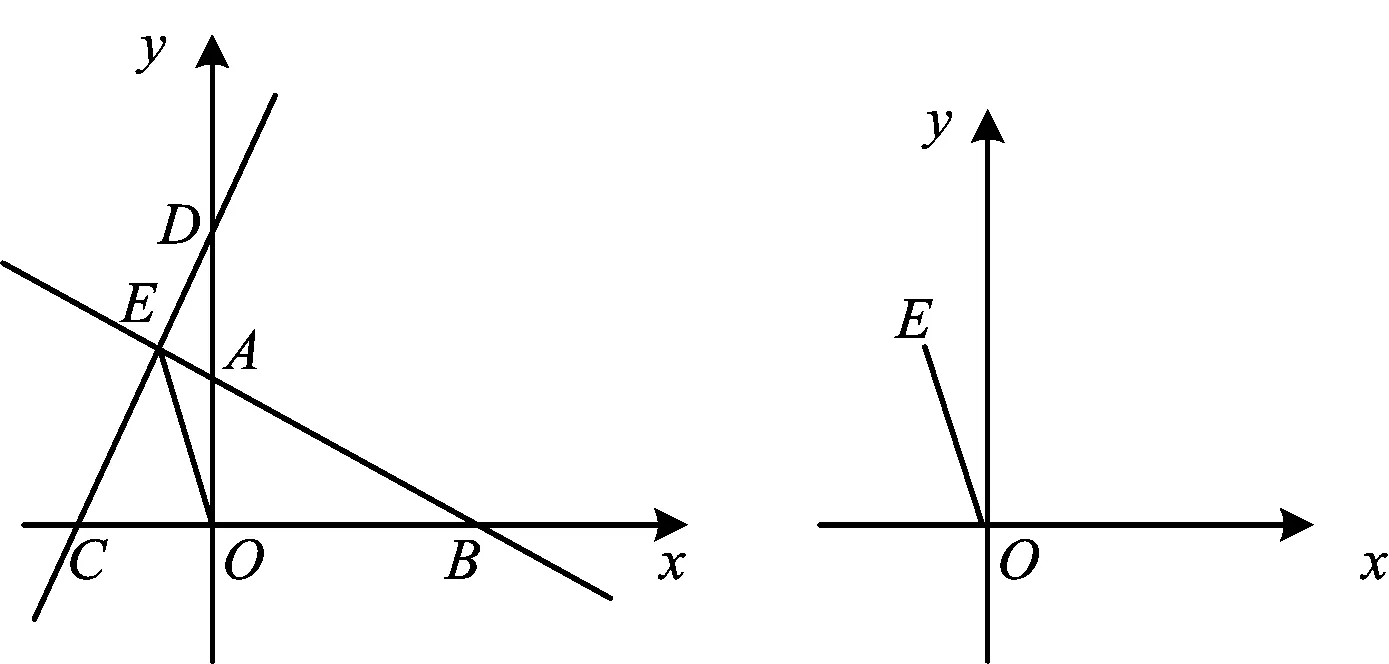
图10图11

分析1)直线CD的解析式为y=2x+2.

②去掉无关的线和点，画出图形如图11.

③构造K字型：如图12，以E为直角顶点，点F位于第一象限；如图13，以O为直角顶点，点F位于第一象限.

图12图13

图14

1)求直线DF的解析式.

2)在第一象限内，是否存在点H，使以G,O,H为顶点的三角形为等腰直角三角形？若存在，求出点H的坐标；若不存在，请说明理由.

比较问题5和变式1，背景稍有改变，问题的实质没有变.

设计意图把基本模型放在较复杂的情境中，要求学生注重对问题本质的理解和对基本模型的挖掘，真正理解模型.

4 应用基本模型解决问题

通过前面的铺垫，再来解决例1，学生就自然而然地会尝试利用45°角构造等腰直角三角形，再构造K字型来解决了.

图15图16

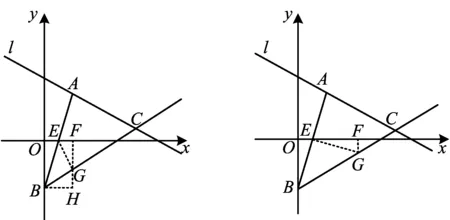
图17图18

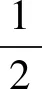
通过模型的铺垫，再让学生解决问题时，学生找到了4种解法，并且总结归纳了这4种方法的共同之处：

1)要求点C的坐标，就是要求两条直线的交点坐标.已知直线AC的解析式，只需求出直线BC的解析式，又点B的坐标已知，故只需再找直线上另一点的坐标即可.

2)都利用45°的特殊角构造直角三角形解决.

3)都是通过构造K字型求解.

图19

5 中考应用实例

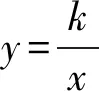
(2017年浙江省金华市数学中考试题第15题)

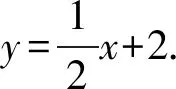
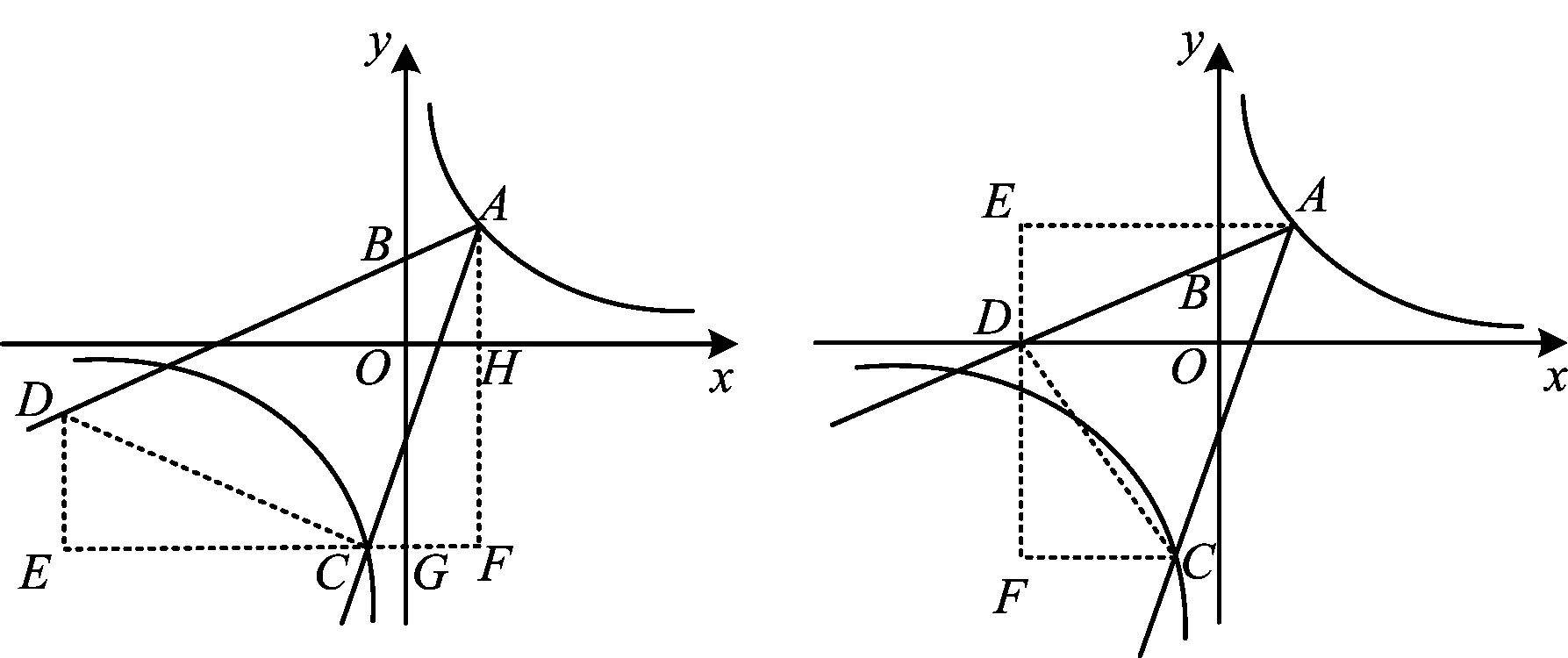
图20图21

设计意图将此题作为课外练习，让学生体会到只要掌握基本方法，中考题也不难解决，从而进一步巩固建模的思想方法，学生学习的兴趣也能得到极大的激发[1].

6 对培养模型思想的两点思考

第一，学生在数学解题时，更多的不是解不出题目，而是想不到该从何处着手.就如例1中学生不知道怎么用45°角的条件，因此在解题教学中，应不断引导学生由特殊条件发现、识别、构造出熟悉的模型，由模型意识来指导解题.当遇到新问题时，先辨识它属于哪一类基本模式，联想起一个已解决的问题，然后以此为索引，在记忆贮存中提取出相应的方法来加以解决.

第二，模型思想的培养是一个日积月累的长期过程，不可能一蹴而就.因此那些常用的数学模型要好好珍惜，如本文所述的“K字模型”，在教学中要加强培养学生的模型意识，让学生深刻认识到数学模型可以使复杂问题本质化、简洁化，甚至一般化，使某类问题的解决有共同的程序式方法.