中低速荷载下FRP与混凝土界面本构模型开发

李晓琴，陈前均,4，陈建飞，陶 毅

(1.昆明理工大学 建筑工程学院, 云南 昆明 650500; 2.贝尔法斯特女王大学 建筑与土木规划学院， 英国 贝尔法斯特 BT9 5AG;3.西安建筑科技大学 土木工程学院，陕西 西安 710055;4.云南震安减震科技股份有限公司，云南 昆明 650217)

纤维增强复合材料(Fiber Reinforced Polymer/Plastic，简称FRP)因其轻质高强、耐腐蚀性和施工性能好等优越性，已经被广泛应用到钢筋混凝土结构加固领域[1].FRP-混凝土界面的粘结性能是确保FRP和混凝土共同受力，充分发挥FRP性能，确保加固效果的关键.FRP-混凝土界面粘结-滑移关系反映了界面的粘结性能，是FRP 外贴加固混凝土结构受力分析的基础，同时界面粘结-滑移模型的精确性是FRP加固混凝土结构设计中的关键因素.

涉及FRP-混凝土界面的有限元应用研究中[9-10]，常在FRP和混凝土单元之间引入Cohesive单元作界面单元，并采用FRP-混凝土界面的切向粘结-滑移关系定义Cohesive单元的切向本构关系，通过Cohesive单元来模拟界面的剪切性能及破坏过程.上述模拟方式须基于准确的FRP-混凝土界面粘结-滑移模型.目前，在FRP-混凝土界面切向粘结-滑移性能有限元研究中涉及加载速率效应的研究较少；并且采用Cohesive单元作为FRP-混凝土界面单元时，缺乏合适的考虑FRP与混凝土界面行为非线性和滑移速率效应的Cohesive单元本构模型.

1 FRP-混凝土界面动态粘结-滑移本构关系

Lu等[2]基于精细单元的有限元模拟方法提出了三种FRP-混凝土界面粘结-滑移模型，分别被命名为精确模型、简化模型和双线性模型.三种模型中，简化模型在保证精度的基础上又具有较为简洁的表达公式，适用于有限元中FRP-混凝土界面单元的本构定义[11]，因此本研究选取Lu等[2]提出的简化模型作为界面单元在准静态下的本构关系.

2 本构模型子程序开发

2.1 已有Cohesive单元材料模型

目前，在最新版本R10.0的LS-DYNA中，直接用于Cohesive单元的材料模型包括： *MAT_138、*MAT_184、*MAT_185、* *MAT_186、 *MAT_240和*MAT_279.Cohesive单元的本构关系一般被认为是为应力和位移之间的关系，上述6种模型中除*MAT_186和*MAT_279以外的其他4种材料模型的切向粘结-滑移本构关系都为线性或多段线性关系.Cohesive单元受荷载作用时，上述4种材料模型都将本构关系的上升段定义为线弹性，随着滑移量的增加，粘结应力线性上升到最大值.之后部分材料模型开始损伤并线性软化.LS-DYNA中另外一个非线性的材料模型是*MAT_279，其本构关系包含线性上升段和指数形的软化段.虽然这两种模型可以反映非线性的本构关系，但却都没有考虑滑移速率效应对本构关系的影响.目前，仅*MAT_240能考虑滑移速率对切向粘结-滑移本构关系的影响，其定义了Cohesive单元有效应变率和αDIF的关系.但此模型的本构关系整体呈梯形形状，不能反映界面非线性性能.

总之，目前LS-DYNA中直接用于Cohesive单元的材料模型，缺乏合适的考虑界面行为非线性和滑移速率效应的本构模型.本文将依据提出的FRP-混凝土界面动态粘结-滑移关系，基于LS-DYNA的材料子程序开发平台进行Cohesive单元本构模型子程序开发.

2.2 本构模型子程序开发

建立LS-DYNA的自定义材料本构模型子程序，需要利用Windows操作平台下的FORTRAN编译器和Microsoft Visual C++，以完成材料模型的程序代码编写.根据LS-DYNA的自定义Cohesive单元材料模型子程序要求，将本文提出的FRP-混凝土界面动态粘结-滑移关系编程.所定义的材料本构模型子程序，在LS-DYNA的求解K文件中采用自定义材料卡片，MAT_USER_DEFINED_MATERIAL_ MODELS调用.根据所定义的子程序及Cohesive单元材料模型的要求，需要在上述材料卡片中定义的材料参数有，材料密度：ρ，建立三维单元时，密度应按体积分布(单位g/mm3)，建立平面单元时，密度按面积分布(单位 g/mm2).还需要定义的材料参数包括混凝土的抗压强度fc(单位 MPa)、混凝土的抗拉强度ft(单位 MPa，当该值置空或定义为0时，子程序将自动计算混凝土的抗拉强度取值)、FRP-混凝土界面的宽度比系数βw、是否考虑滑移速率的影响的控制参数等.

3 子程序测试与验证

采用所开发的本构模型子程序进行了单个Cohesive单元验证试验，即以单个单元作为计算模型，利用开发的子程序赋予单元材料特性，进行单元在纯剪切条件下的计算，并将LS-DYNA的计算结果与本研究提出的动态粘结-滑移本构关系对比.

3.1 单个Cohesive单元模型的建立

在LS-DYNA中建立单个Cohesive单元，单元设置成边长为10mm的立方体.单元的纯剪边界条件如图1所示，即1到8号节点约束X和Y方向的位移恒为0，令1、2、3和4号节点发生沿Z轴正方向的位移，同时令5、6、7和8号节点发生沿Z轴负方向的位移.为了避免初始加速度对LS-DYNA的计算结果造成影响，通过*DEFINE_CURVE_SMOOTH的方式控制各个节点的速度，以实现位移控制加载，采用这种加载方式同时可以获得本构关系的下降段.加载过程中节点1、2、3、4与节点5、6、7、8上的速度大小应保持相同，方向相反.

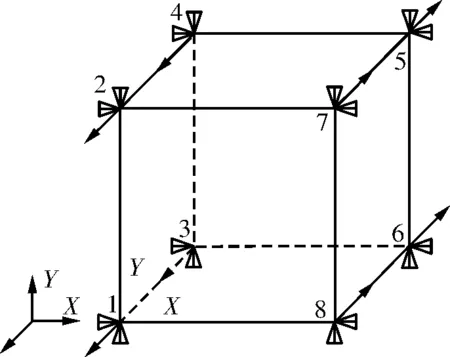
图1 单个Cohesive单元纯剪边界条件Fig.1 Pure shear constraints of single cohesive element

3.2 不考虑滑移率效应的子程序验证

采用本研究开发的本构模型子程序对上述单个Cohesive单元进行材料本构定义，首先在不考虑滑移率效应情况下对子程序进行验证.用于本构模型定义的材料参数包括：混凝土的抗压强度：fc= 30 MPa，混凝土的抗拉强度：ft= 3 MPa；FRP-混凝土宽度比系数：βw= 0.707.采用上述材料参数，基于本研究提出的本构关系可以确定具体的FRP-混凝土界面粘结-滑移本构关系，如图3所示.在单个Cohesive单元模型的有限元计算结果中，可以获得单元的粘结应力和界面相对滑移量等信息，可以绘制两者的关系，即LS-DYNA的本构关系计算结果，其反应也就是子程序所实现的本构关系，将该曲线一并绘制于图2中.

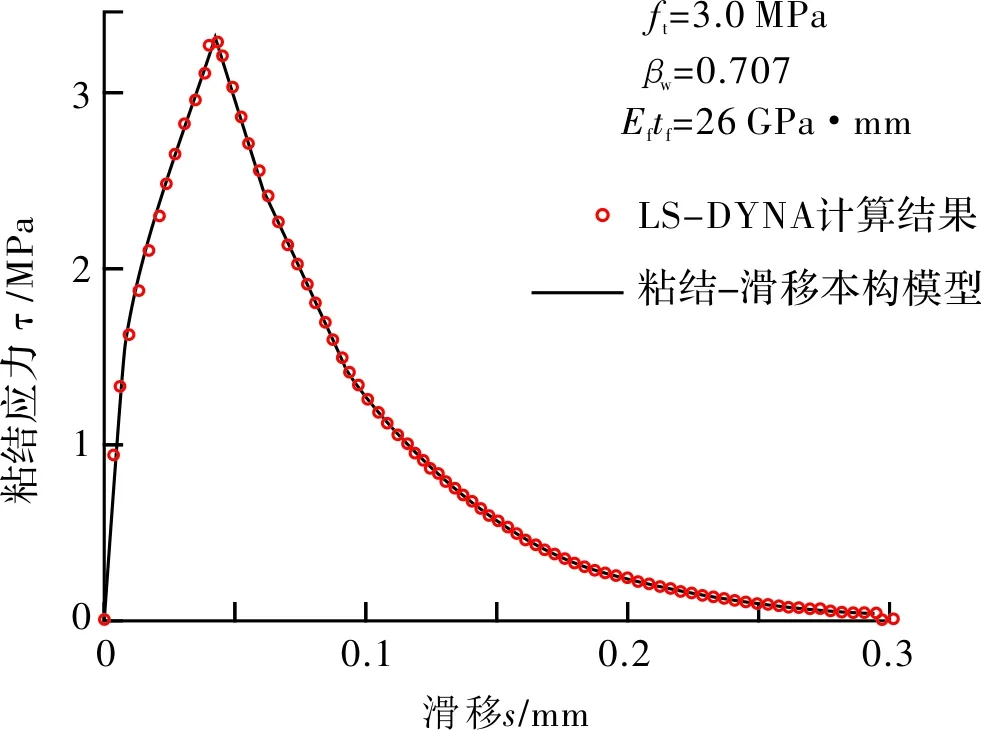
图2 子程序计算结果和本构模型对比Fig.2 Comparison of subroutine calculation resultswith constitutive model

采用自定义的材料子程序时LS-DYNA的计算结果和本研究提出的粘结-滑移关系完全重合.分析具体的计算结果，LS-DYNA计算出的最大粘结应力约为3.351 5 MPa，对应的界面滑移量约为0.043 6 mm，极限滑移量约为0.293 2 mm，而基于材料参数的本构关系中最大粘结应力为3.352 5 MPa，对应的界面滑移量为0.043 6 mm，极限滑移量为0.292 9 mm.对比发现三组数据都十分接近，其误差不超过0.1%.上述结果表明开发的本构模型子程序在不考虑滑移率效应的情况下，计算结果是合理的且稳定的，所开发的子程序符合FRP-混凝土界面非线性性能的要求.

3.3 考虑滑移率效应的子程序验证

仍采用上述单个Cohesive单元模型，在考虑滑移率效应情况下对子程序进行验证.为了得到不同的滑移速率下的计算结果，对于加载方式需要进一步控制，在*DEFINE_CURVE_SMOOTH卡片中，控制加载最大速率分别为：0.5×10-7m/s、0.5×10-5m/s和0.5×10-3m/s以实现不同的滑移速率.因为模型的加载设置中，控制单元相对两个面上节点的速度大小相同，方向相反，因此，基于上述加载速率，模型相对表面实际的滑移率是加载速率的2倍.其他材料参数设置与3.1节中的设置完全相同.基于本研究提出的动态粘结-滑移本构关系和上述材料参数，不同滑移率下的本构曲线如图3所示.同样LS-DYNA的计算结果中，也可以获得不同加载速率下单元的粘结应力与滑移量等信息，由LS-DYNA的计算结果绘制的粘结-滑移曲线一并绘制于图3中.

在考虑滑移率效应时，本构模型子程序在不同滑移率下的粘结-滑移曲线模拟结果与考虑αDIF的动态粘结-滑移本构曲线完全重合.进一步对比不同滑移率下的最大粘结应力及其对应的滑移量与极限滑移量的具体数值，有限元模拟结果与动态本构关系计算结果，两者对应数值的相对误差都不超过0.5%，说明所开发的子程序符合FRP-混凝土界面考虑加载速率效应的要求.

图3 不同滑移率时的计算结果与动态本构模型对比Fig.3 Comparison of calculation results with dynamicconstitutive models at different slip rates

4 结语

针对中低速荷载作用下FRP与混凝土界面的粘结-滑移本构关系进行了研究，并基于提出的FRP-混凝土界面动态粘结-滑移本构模型，进行了Cohesive单元材料模型子程序本构开发.对所提出的本构模型子程序进行了单个Cohesive单元纯剪状态的模拟验证，模拟结果表明，所开发的本构模型子程序在中低速荷载下满足界面性能非线性和考虑加载速率效应的要求.