超宽混凝土主梁斜拉桥收缩徐变效应分析

黄 新，贾 烊，李建慧，王 涛

(1. 南京林业大学 土木工程学院，江苏 南京 210037；2.南京市政设计研究院有限责任公司，江苏 南京 210008)

作为混凝土的固有时变特性，收缩徐变能够在较长时间内引起混凝土变形.收缩徐变变形受到约束后会在混凝土构件内部产生附加应力[1].为了计算混凝土构件的收缩徐变效应，学者们在试验的基础上提出了一系列收缩徐变预测模型，其中CEB-FIP1990预测模型为我国公路桥梁设计规范所采纳[2-3].计算理论方面，将按龄期调整的有效模量法(AEMM)结合有限单元步进法(FEM)，便于编制程序计算混凝土构件的收缩徐变效应[4-5].

斜拉桥属高次超静定结构，收缩徐变作用下斜拉桥结构的力学响应受到了国内外研究者的广泛关注.根据周履[6]的介绍，英国迪河斜拉桥的工程师通过修正预测模型预估收缩徐变变形量，在主梁线形控制方面取得了良好的效果.陈太聪等[7]基于等效增量荷载原理编制了混凝土主梁斜拉桥节段施工收缩徐变计算程序.苏成等[8]基于响应面-蒙特卡罗法对一座独塔双索面斜拉桥进行了收缩徐变随机分析.而与普通宽度主梁斜拉桥相比，超宽主梁斜拉桥混凝土用量大且一般均设置有多道横梁.超宽主梁在纵横向预应力和拉索力的共同作用下内力分布状况复杂，而混凝土徐变与构件应力状态密切相关，因此有必要研究超宽混凝土主梁斜拉桥的收缩徐变效应.斜拉桥收缩徐变受材料组成、施工工艺和环境条件等因素耦合作用[9]，现有文献对超宽混凝土主梁斜拉桥的收缩徐变参数敏感性研究较少.本文依托实际工程，建立超宽混凝土主梁斜拉桥全桥梁格模型，基于AEMM-FEM法和灰色关联度方法对该桥进行收缩徐变参数敏感性分析.

1 工程概况

某独塔双索面斜拉桥跨度为185 m(100 m+85 m)，塔柱为椭圆型钢箱混凝土结构，为墩塔梁固结体系，全桥布置情况如图1所示.主梁和桥塔均采用C50混凝土，斜拉索与预应力钢束材料分别为钢丝和钢绞线.超宽主梁采用双边箱形式，边箱结构为预应力混凝土单箱双室，桥面宽为37 m，主梁横断面如图2所示.

图1 全桥布置图(单位：cm)Fig. 1 Layout of the bridge (Unit: cm)

图2 主梁横断面(单位：cm)Fig.2 Cross section ofthe girder (Unit: cm)

2 有限元建模

2.1 全桥空间梁格模型

利用Midas/Civil有限元软件建立全桥空间梁格模型，由于超宽主梁具有腹板距离大、翼缘板宽且箱壁薄的特点，为了准确反映结构的受力特性，采用剪力-柔性梁格法[10]模拟超宽混凝土主梁，将主梁划分为6根纵梁.桥塔和斜拉索分别采用梁单元和只受拉桁架单元模拟，在模型中考虑的荷载作用主要包括自重、拉索力、预应力、二期恒载和城-A级汽车荷载.根据设计资料划分施工阶段：主塔和边跨主梁施工时间共计150 d；主跨主梁各节段悬臂浇筑施工时间为15 d；在主跨主梁各节段的施工过程中，对称张拉两侧斜拉索的时长为2 d；施工桥面铺装和附属设施、拆除支架的持续时间共计35 d.全桥有限元模型见图3，在表1中列出了模型的边界条件，主要构件的材料参数见表2.

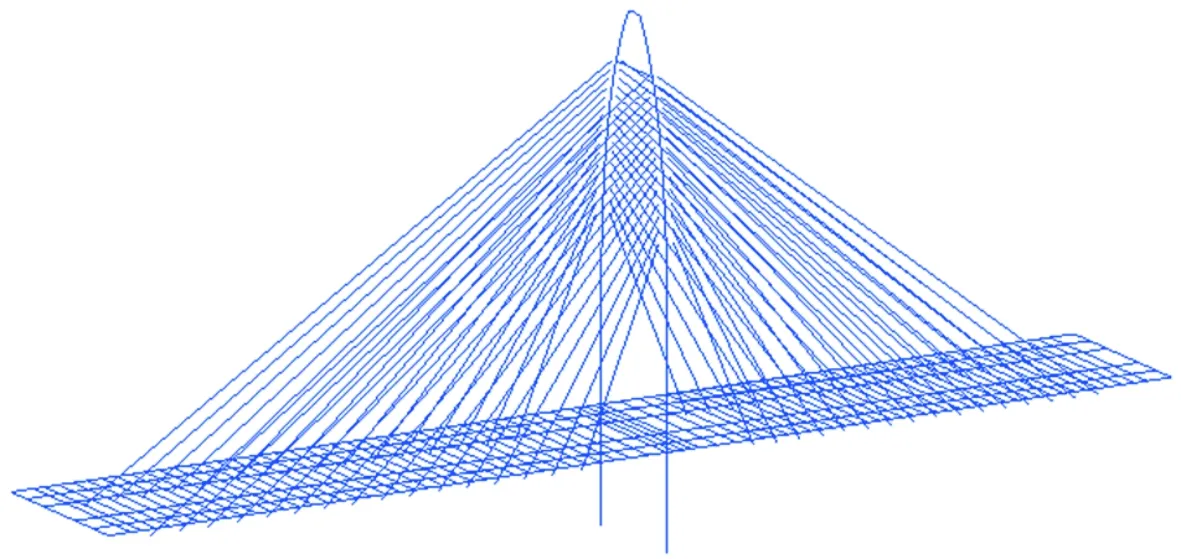
图3 全桥空间梁格模型Fig.3 Spatial grillage model of the bridge

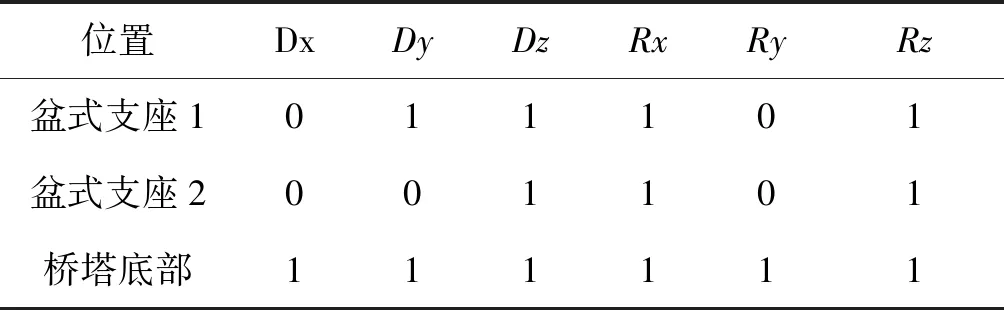
位置DxDyDzRxRyRz盆式支座1011101盆式支座2001101桥塔底部111111

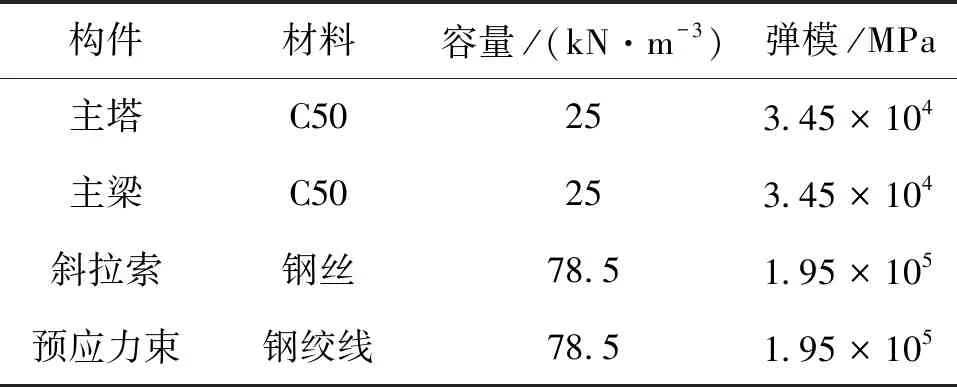
表2 主要材料参数

2.2 模型验证

为了验证有限元模型的准确性，进行全桥动力特性试验.沿纵桥向选取主梁振动测试截面，J1～J3截面位置为主跨主梁三分点， J4截面位于边跨主梁跨中，图4为现场试验情况.在环境激振作用下得到前4阶结构固有振动频率实测值和模型理论值，分析结果如表3所示.

图4 现场试验图Fig.4 Photos of field test

阶数实测值/HzJ1J2J3J4理论值/Hz最大误差/%11.891.951.911.911.921.5623.523.733.773.863.694.6133.724.214.144.384.129.7145.015.615.635.815.358.59

由表3可知，在相应振型阶次下主梁固有振动频率实测值与理论值较为接近，最大误差值均在10%以内，说明空间梁格模型结构刚度与实际情况基本吻合，此模型可以作为收缩徐变参数分析的基准模型.

3 计算理论

3.1 AEMM-FEM收缩徐变分析方法

试验结果表明，当混凝土应力低于其极限强度的40%～50%时，终极徐变变形与初始弹性变形近似呈线性关系，分批加载应力后产生的应变可以叠加[11].Bazant教授据此推出混凝土收缩徐变总应变增量表达式：

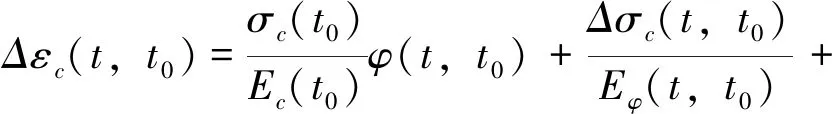
(1)

式中，Eφ(t,t0)为按龄期调整后的混凝土弹性模量；φ(t,t0)为徐变系数；εcs(t,t0)为收缩应变.

将施工过程细化为若干个计算时段，则在单个时段内收缩徐变产生的应力增量与应变增量为线性关系，可以利用有限单元法和逐步递推法迭代计算混凝土收缩徐变引起的内力和位移.

3.2 灰色关联度分析方法

灰色关联度分析方法通过计算关联度序列，得到元素对于系统的影响敏感性差异[12]，步骤如下：

(1)原始数据矩阵的无量纲化处理：选择m个敏感性参数组成自变量比较矩阵，每种参数包括n个取值，相应的系统影响值组成因变量参考矩阵.以自变量矩阵元素为例，对原始数据矩阵元素作均值无量纲化处理.

(2)

(2)确定灰色关联差异信息矩阵：对自变量矩阵与因变量矩阵各元素逐一进行差值绝对化计算建立差异信息矩阵Δ，提取Δ中的最大值M与最小值m，计算关联系数.

(3)

(4)

为了强化关联系数之间的差异性，分辨系数δ取0.5.

(3)计算灰色关联度序列：对同一自变量的关联系数取平均值作为该自变量与系统因变量之间的关联度.

(5)

将关联度按数值大小进行排序，关联度越大说明该因素对系统影响的敏感性越大.排序结果与采取的数据处理方法无关，分析结果具有可靠性.

4 收缩徐变效应分析

4.1 混凝土收缩徐变参数设置

采用CEB-FIP1990预测模型反映混凝土材料的收缩徐变规律，选择主梁加载龄期X1、混凝土收缩龄期X2、环境相对湿度X3、主梁混凝土强度X4作为参数分析的变量.将基准模型的成桥运营时间统一设置为100 d，桥塔加载龄期为7 d，基准模型的X1、X2、X3、X4分别取10 d、3 d、70%和50 MPa.

4.2 超宽主梁负弯矩区影响分析

提高混凝土收缩徐变参数值，超宽主梁最大负弯矩截面上、下缘压应力变化如图5所示，超宽主梁最大负弯矩变化分别如图6所示，负值代表截面压应力或负弯矩减小.

图5 压应力变化Fig.5 Change of compressive stress

图6 最大负弯矩变化Fig.6 Change of maximum negative moment

由图5和图6可知，在超宽主梁最大负弯矩位置中，截面上、下缘压应力和负弯矩均随着主梁加载龄期、抗压强度和环境相对湿度的增加而减少.其中，环境相对湿度升高引起的下缘压应力和负弯矩变化量最大，减少率分别达14.57%和8.99%.截面上缘压应力变化量小于下缘，这是由于负弯矩区主梁顶板厚度小于底板，而顶板配筋率大于底板，在钢筋的抑制作用下，收缩徐变对主梁截面上缘应力的影响相对较小.上、下缘应力和弯矩变化值在横截面上分布不均匀，整体呈波浪形曲线，可知超宽主梁收缩徐变的空间效应显著.由于斜拉索锚固在主梁底板，斜拉索预埋管处于中腹板范围内，索力荷载对中腹板应力状态的影响较大，进而影响中腹板的徐变效果.同时，超宽主梁中腹板厚度大于斜腹板，收缩徐变对中腹板的影响更大.因此，超宽主梁中腹板对收缩徐变参数更为敏感.

4.3 索力影响分析

超宽混凝土主梁斜拉桥斜拉索具有数量多、空间分布广、索力均衡性要求高的特点，索力分布状态影响结构整体受力性能.篇幅所限，仅列出收缩徐变各参数影响下单侧索力的变化情况，数据如图7所示，负值代表索力减小.

从图7可以看出，提高主梁加载龄期、主梁抗压强度和环境相对湿度对索力的影响趋势一致：跨中区域斜拉索发生应力松弛现象，梁端附近斜拉索的索力负担加重.其中，主梁抗压强度变化引起的索力下降幅度最大，跨中区域索力松弛率达1.44%.环境相对湿度从70%提高至98%，Z16号索的内力增长率达4.42%.这是由于在混凝土收缩徐变的作用下，桥塔和主梁均会产生结构变形，拉索锚固点偏离初始几何位置，导致索力不均衡程度加剧.

4.4 收缩徐变参数敏感性分析

选择主梁最大挠度Y1、塔顶纵向偏移距离Y2作为结构变形程度的评价指标.分析时改变基准模型的某一参数，控制其他参数不变，基准模型的参数取值情况如前所述.不同收缩徐变参数条件下，超宽混凝土主梁斜拉桥结构线形的响应值见表4.

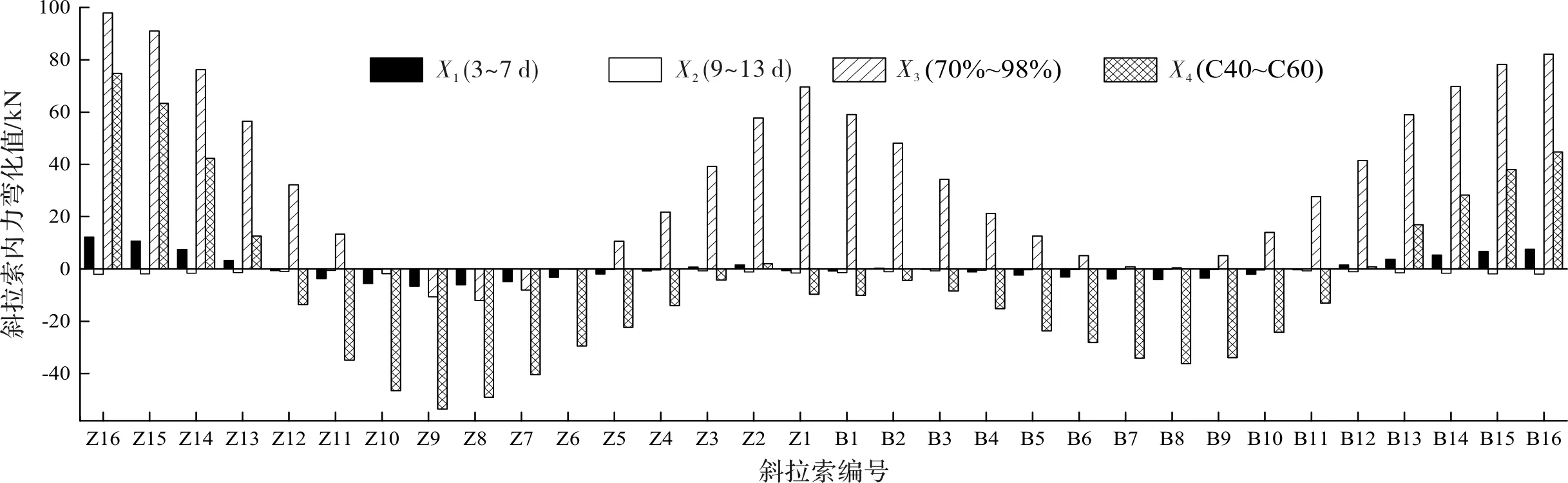
图7 斜拉索内力变化Fig.7 Change of internal force of stay cables

收缩徐变参数X主梁挠度最大值Y1/mm塔顶纵偏值Y2/10-2mmX1/dX2/dX3/%X4/MPaY1Y2Y3Y4Y1Y2Y3Y4937040-68.15-67.65-67.65-72.92-366.48-368.64-368.64-334.341047745-67.65-67.70-64.41-70.09-368.64-368.78-365.80-352.441158450-67.21-67.74-61.01-67.65-370.52-368.93-362.20-368.641269155-66.81-67.80-57.76-65.52-372.15-369.10-357.91-383.331379860-66.45-67.86-56.36-63.84-373.62-369.29-353.53-391.22

注：负值代表坐标轴负方向

由表4的数据可知，环境相对湿度、主梁加载龄期增加，超宽主梁挠度均呈减小趋势.这是由于混凝土构件在湿度较大的环境下材料吸附水蒸发量减少，使得混凝土的水泥水化反应更加充分，收缩徐变效应得到减轻.加载前，混凝土在自重作用下发生初始收缩徐变变形，而收缩徐变变形总量趋于收敛，提高主梁加载龄期将会压缩构件使用期间的收缩徐变发展空间.加载龄期增加后，混凝土在使用阶段弹性模量的起点较高，在一定程度上限制了构件徐变变形能力.桥塔变形方面，仅环境相对湿度的升高会缓解塔顶纵向偏移程度.其中，主梁抗压强度变化引起的塔顶位移最大，抗压强度从C40提高至C60，塔顶偏移变化率达17.01%.

对表2中的数据进行初始列阵，按照灰色关联度方法进行数值计算.收缩徐变参数与超宽主梁挠度之间的关联度矩阵为

收缩徐变参数与塔顶纵偏值之间的关联度矩阵为

按数值大小对灰色关联度进行排序，结果为

由灰色关联度序列可知，主梁加载龄期是影响超宽主梁线形的最敏感因素，其次是主梁抗压强度、环境相对湿度、收缩龄期的影响.塔顶位移受主梁抗压强度的影响最为严重，主梁加载龄期、环境相对湿度和收缩龄期的影响依次递减.

5 结论

通过对超宽混凝土主梁斜拉桥进行收缩徐变参数敏感性分析，得出如下结论：

(1)主梁加载龄期、抗压强度和环境相对湿度变化时，超宽主梁负弯矩区截面应力与弯矩变化值沿横向分布不均，索力不均衡现象凸显.为保障结构的使用安全，设计时应对收缩徐变相关材料参数合理取值，同时考虑环境湿度季节性变化对结构受力性能的影响.

(2)根据灰色关联度分析结果，主梁加载龄期是影响超宽主梁线形的最敏感因素.超宽主梁挠度随着主梁加载龄期的增大而减小，施工时应为主梁早期收缩徐变留足时间，以减轻收缩徐变的不利影响.