基于最小外接矩形的集料颗粒形状特征快速评价方法研究

曹源文，杨国林，张莹莹，王若俊，程志豪

(1. 重庆交通大学 机电与车辆工程学院，重庆 400074； 2. 云南省交通规划设计研究院，云南 昆明 650041；3. 云南玉楚高速公路投资开发有限公司，云南 昆明 650041)

0 引 言

集料颗粒是沥青混合料的主要组成部分，其占比约为95%。工程技术人员对路面早期破坏因素作了相关研究，发现集料级配及形状特征对沥青路面的使用性能及耐久性有较大的影响。当混合料中针片状颗粒数量较多时，沥青路面的强度和抗车辙性能下降，抗水损害能力降低。同时，针片状颗粒越多，碾压作业过程中压碎、压溃现象越明显，对沥青路面的压实度以及离析情况均有一定的影响[1]。

针片状颗粒主要产生于机械设备进行破碎的过程中，其含量受破碎机械设备的型式、性能以及加工母岩的构造特征等因素影响，因此需要对针片状颗粒含量进行检测，才能找出破碎机械性能参数及母岩的适配程度。然而传统人工检测方法效率很低，目前多采用图像处理的方法来提高工作效率。图像处理中集料的平面轮廓近似模型有等效圆、等效椭圆和等效矩形[2]，其中以等效矩形模型的使用较为普遍。

由于集料轮廓的形状较为复杂，且多为凸边、凹边。为了获得更好的等效矩形，目前一般采用面积最小外接矩形和周长最小外接矩形两种方法。而最小外接矩形的求解算法以旋转算法[3-6]、扫描算法[7]、顶点链码算法[8]为主。其中旋转算法目前有等间隔旋转算法、形心旋转算法、主轴旋转算法和凸壳旋转法。程鹏飞等在求解多边形最小面积外接矩形[9]时，利用图形学知识已经证明多边形的最小外接矩形必定过该多边形凸边的一条边界。因此笔者采用凸壳边界旋转算法，对集料颗粒进行形状特征研究，并对这种算法进行改进，缩短算法运行时间。最后通过实例分析，可以实现快速计算出集料颗粒的扁平率。

1 边界旋转法及改进

1.1 凸壳函数算法

凸壳算法在模式识别、图像处理、图形学和人工智能方面有着广泛的应用，很多问题都可以归纳为凸壳问题求解。计算平面点集凸壳的算法通常有卷包裹法、格雷厄姆法、分治算法、增量算法和近似算法等。其中，格雷厄姆算法是解平面点集凸壳问题中的时间复杂性最小算法[10]。

1.1.1 格雷厄姆算法

格雷厄姆算法基于凸多边形的各顶点必在该多边形任意一条边的同一侧的原理。该方法的步骤：①找到S点集中纵坐标最小的点P1，把P1同点集中其它各点用线段连接，并计算这些线段与水平线的夹角，然后按夹角大小及到点的距离进行分类，得到一组序列，然后依次连接这些点，便得到一个多边形；②从P1开始按顺序选取相邻两个点组成一条线段，再对其余的点进行判断是否都在这条线段的同一侧，若满足，则继续选取下一条线段进行上述判断，若不满足其余点在同一侧，则将当前线段的末端点删去，后面的顶点依次补上，再进行循环判断，最终走完所有的顶点，得到最后的凸壳边界顶点集。

1.1.2 集料凸壳处理

在工程实际中，集料本身的形状复杂不规则，加上集料表面存在很多白色斑点、棱角纹路等，导致拍摄的图片也会存在一些缺陷。因此采用格雷厄姆算法将复杂图像近似填充为凸多边形，有利于集料颗粒形状特征的研究。对集料进行凸壳拉伸处理，处理效果如图1。

从图1可以看出，格雷厄姆算法得到的凸壳是包含集料复杂图像点集的最小凸集。其中凹边特征被拉伸为凸边，原有的凸边则被保存下来，使得不规则的复杂形状轮廓得到较好的转换。

图1 集料的凸壳处理Fig. 1 Convex hull treatment of aggregate

1.2 凸壳边界旋转算法

1.2.1 确定边界值

根据凸壳边界的顶点坐标，分别找到x轴和y轴方向上最大值和最小值，将其作为边界旋转的初始最小外接矩形，记录下当前的外接矩形的面积及边界最大、最小坐标。

1.2.2 边界旋转

首先求出凸壳边界上每条线段相对水平方向的夹角。假设凸壳边界上第i个点的坐标为(xi,yi)，第i条线段的水平夹角为θi，则计算公式为：

(1)

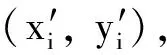
(2)

确定旋转后的凸壳边界在x轴和y轴方向上最大值和最小值，将其作为旋转后的最小外接矩形，计算并记录下当前的外接矩形的面积和旋转的角度及边界最大、最小坐标。

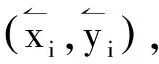
(3)

旋转演示过程如图2。

图2 旋转过程示意Fig. 2 Rotation process indication

将旋转回原图像区域上的坐标记录并保存，然后根据此坐标便可计算出外接矩形面积。

1.2.3 确定最小外接矩形

重复进行边界旋转，将旋转次数记为m，凸壳边界顶点个数记为n。如果第m+1次旋转获得的最小外接矩形比第m次要小，则保留第m+1次的最小外接矩形，且将其显示到图像中，否则将继续进行边界旋转，直到所有的边界旋转完成。至此需要的最小外接矩形已经确定，选择其中面积最小的一个外接矩形作为集料的近似最小外接矩形，如图3。

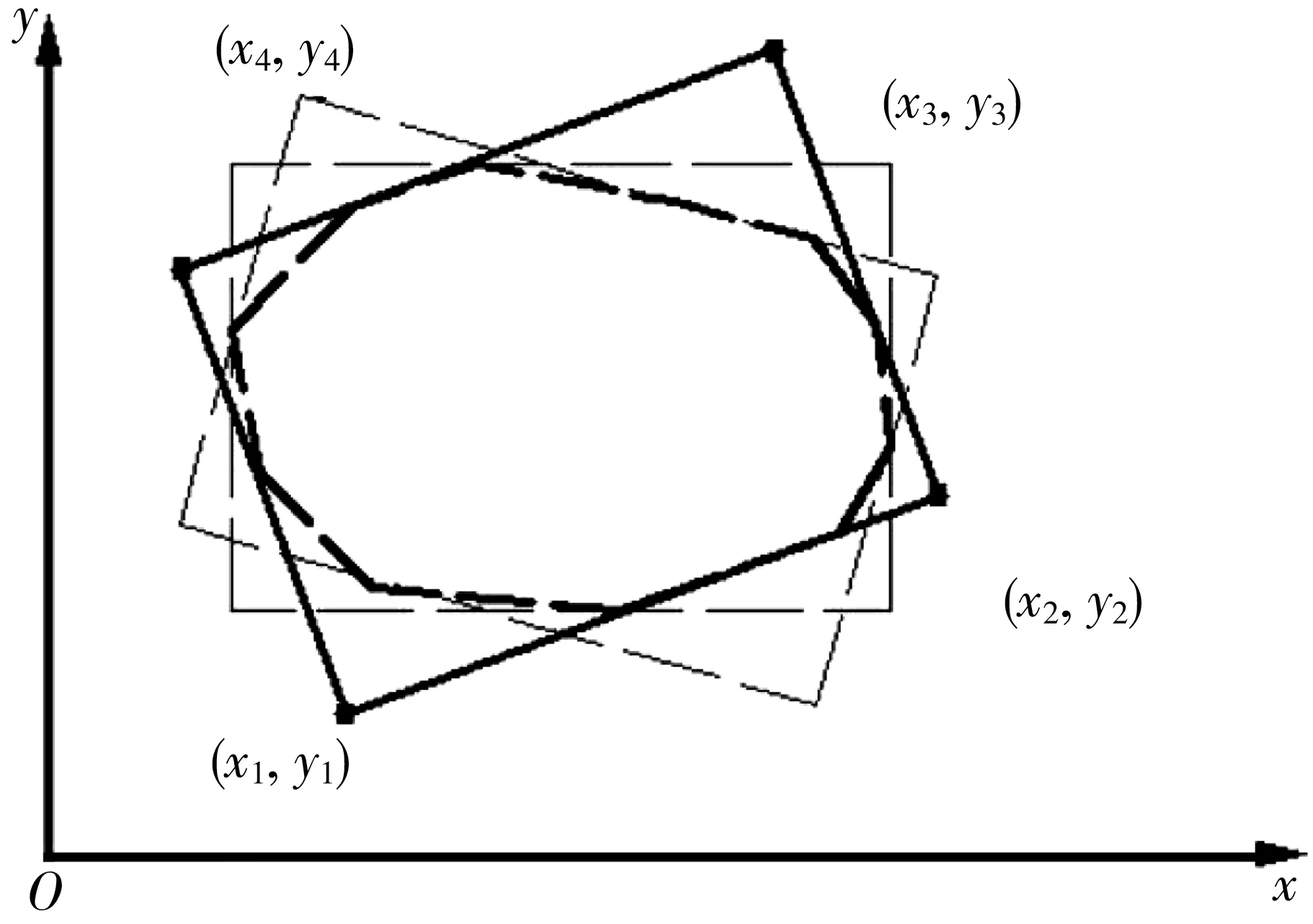
图3 最小外接矩形Fig. 3 Minimum outer rectangle

1.3 算法改进

由于集料图形轮廓凸边较多且复杂，可能存在相同水平夹角，导致边界旋转次数增加。因此需将这些夹角统一化到第一象限内，可以减少旋转次数，提高算法运行效率。假设统一化后的水平夹角为θ，则统一化公式为：

θ=mod[θi/(kπ+π/2)] (i≤n且k∈Z)

(4)

然后取出θ中相同的角度，将其他重复的水平夹角删除，然后把最新的θ带入边界旋转算法进行求解。

2 实例分析

2.1 算法求解对比

利用图像处理技术，将集料标记序号，然后采用最小面积外接矩形的边界旋转算法进行求解，为了便于图像观察，只把求过程中小于当前外接矩形的矩形图像进行显示。其运行过程及结果如图4。

从试验图像中可以得出，两种算法结果一致，且改进后的凸壳边界旋转算法在求解集料轮廓最小面积外接矩形具有更好的时效性。

2.2 可行性分析

由图4可以看出，采用边界旋转算法和改进后的算法结果相同，说明了改进算法的可靠性。根据多次求取原始算法和改进算法的运行时间及旋转次数，得到算法及改进前后的平均旋转次数与耗时。

图4 边界旋转算法运算过程及结果Fig. 4 Operation process and results of boundary rotation algorithm

采用改进后的凸壳边界旋转算法、运行过程及结果如图5。在旋转次数和耗时上的提高效率如表1。

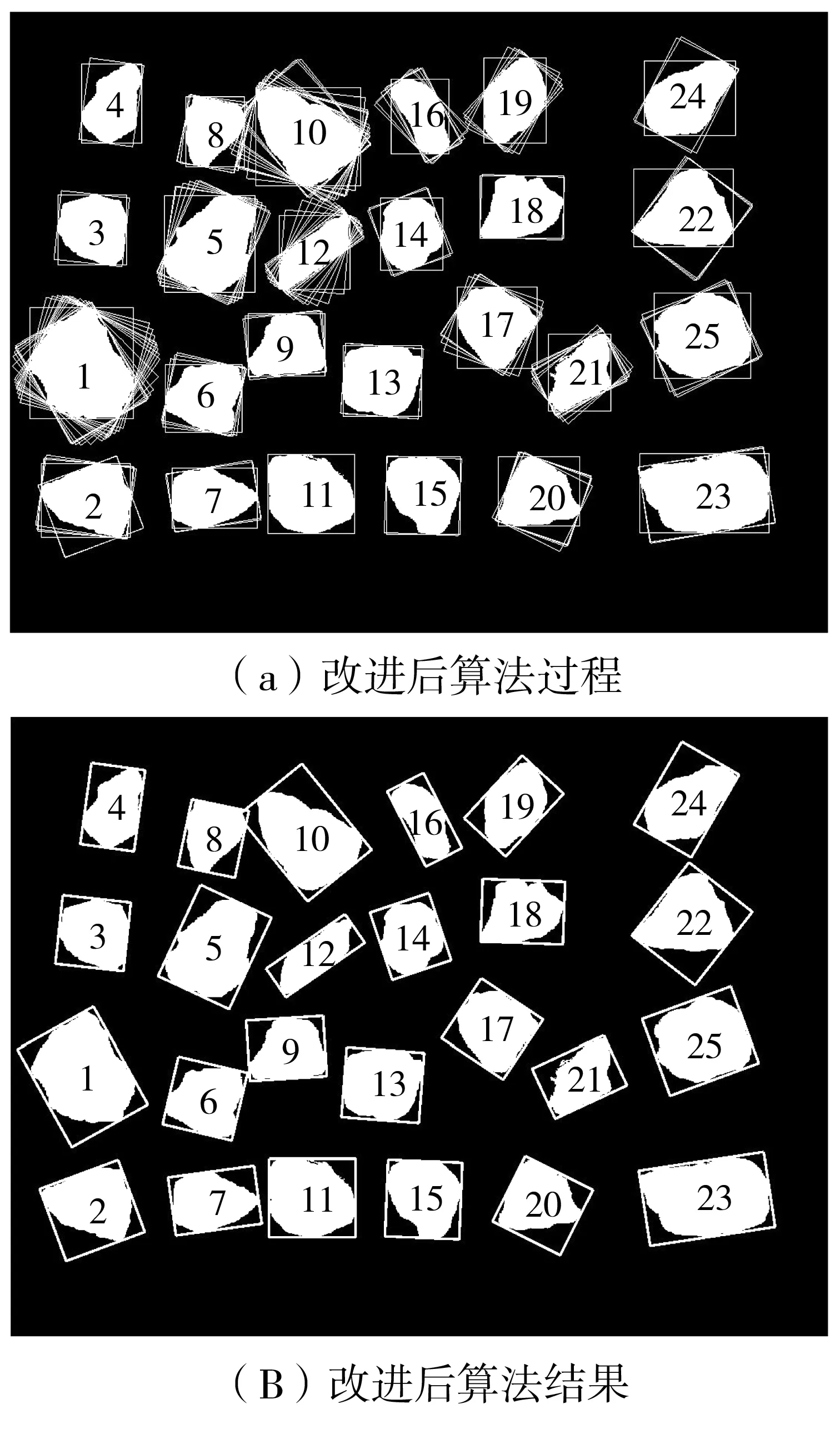
图5 算法改进后的运算过程及结果Fig. 5 Operation process and results of the improved algorithm

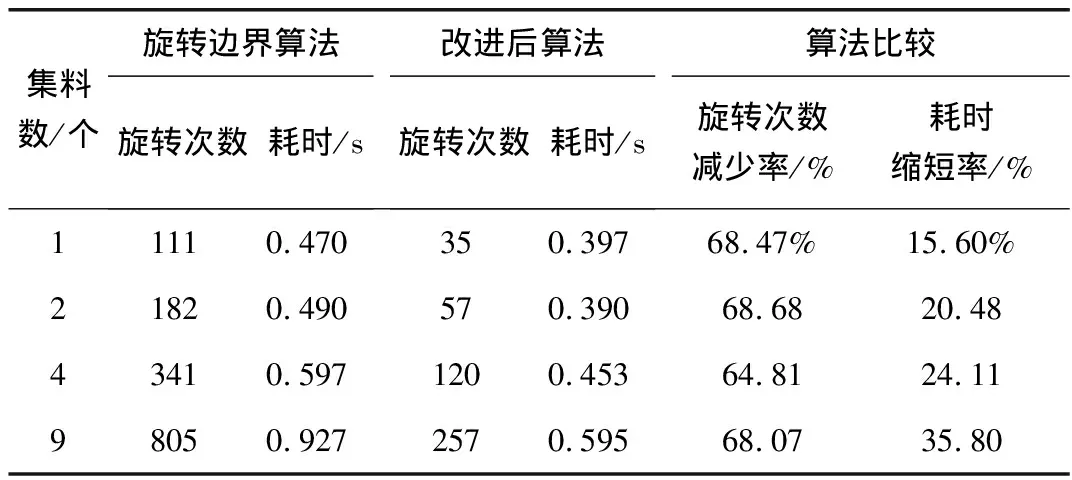
//s/s/%/%11110.470350.39768.47%15.60%21820.490570.39068.6820.4843410.5971200.45364.8124.1198050.9272570.59568.0735.80

由表1可以得出：采用改进后旋转算法，平均旋转次数减少67.5%。随着求解集料个数的增加，算法运行耗时缩短率也随着提高，图像中集料个数较少时耗时缩短率增加并不明显。而随着集料个数大量的增加，算法耗时大幅度的降低。

2.3 误差分析

对于任意一个集料颗粒，扁平比等于该集料最大长度与最大宽度的比值：

(5)

式中：lmax、bmax分别为最小外接矩形的较长边和较短边。

扁平比μ(μ≥1)的值越大，则该集料颗粒形状就越趋向于片状。而当扁平比μ的值越接近1时，集料形状越接近于方形。经图像处理和人工测量得到集料多次测量的尺寸参数平均值如表2。

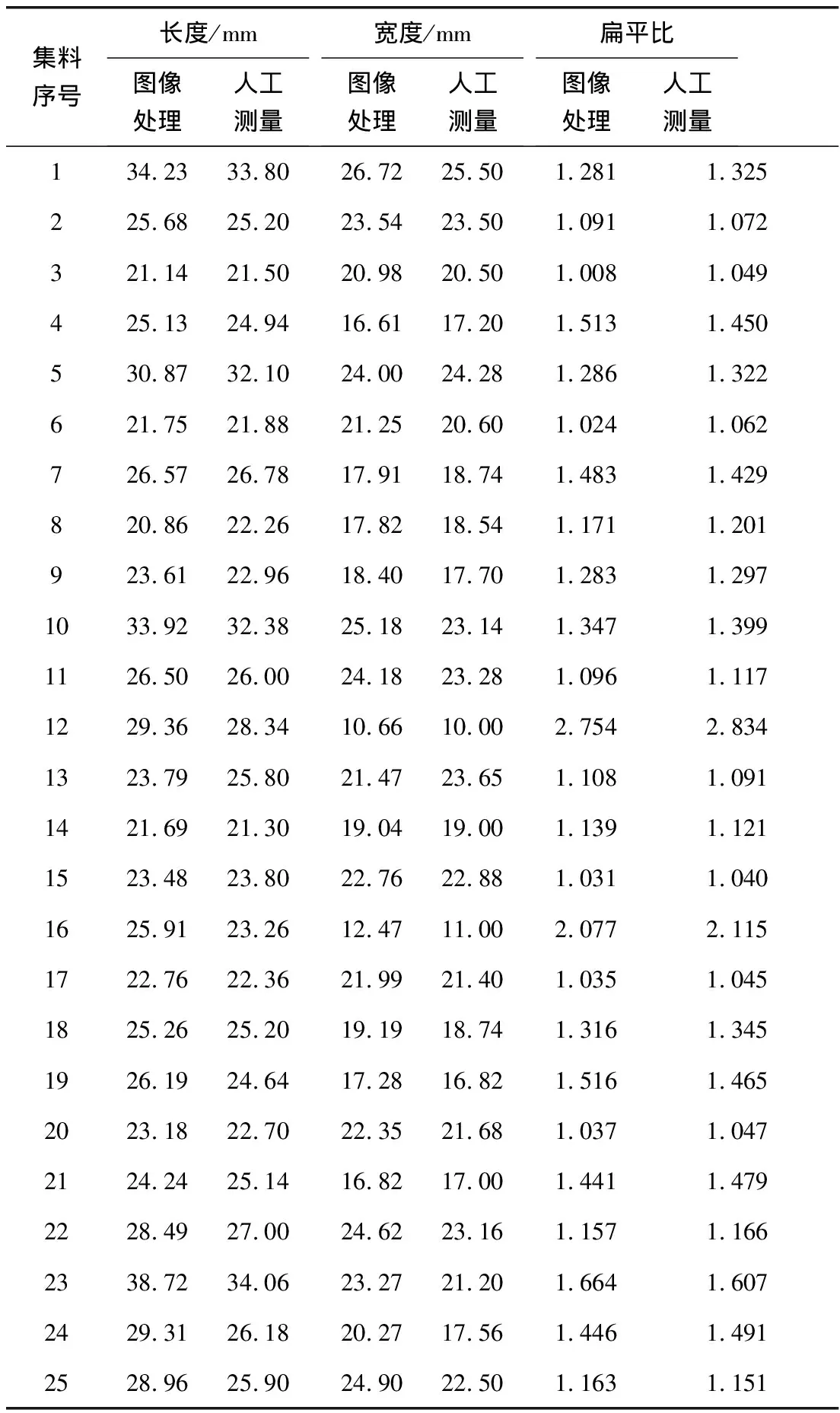
表2 图像处理和人工测量得到的集料颗粒尺寸参数Table 2 Size parameters of aggregate particle obtained byimage processing and artificial measurement

(6)

(7)

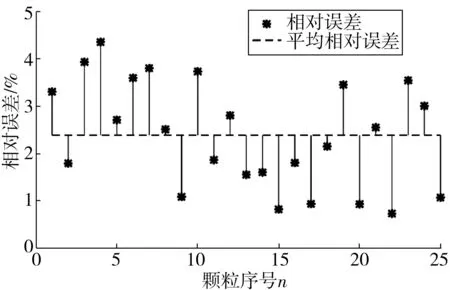
图6 相对误差散点图Fig. 6 Relative error scatter plot

3 结 论

1)针对集料颗粒本身形状复杂，棱角纹路多等问题，提出了应用格雷厄姆算法将复杂图像进行凸壳处理，降低了图像的来源误差。

2)对凸壳边界旋转算法进行了改进，并得到改进前后的时间缩短率曲线。结果表明：处理的集料颗粒数越多，耗时缩短率越明显。改进后的算法可应用于批量集料颗粒的形状特征评价。

3)通过实例分析，得到了图像测量与传统游标卡尺测量扁平比的最大相对误差为4.35%，平均相对误差为2.40%，表明了笔者算法具有较好的准确性。