基于VISUM交通仿真和OD矩阵反推技术的交通预测模型研究
2019-06-13王中立重庆交通大学土木工程学院重庆400074
文/王中立 重庆交通大学 土木工程学院 重庆 400074
张沈越 武汉理工大学 汽车工程学院 湖北武汉 430070
1、绪论
1.1 问题提出
交通需求预测,是交通规划的核心内容之一[1]。早在上个世纪,西方发达国家在大规模城市道路交通规划和建设过程中,逐渐形成了“四阶段”城市道路需求预测技术。四阶段(four-step)模型是指将需要完成的交通需求预测任务划分为四个子任务,即交通产生量预测、OD分布预测、交通方式分担预测和交通量分配预测。
“四阶段”技术在长期的城市交通规划实践中得到了检验,自该方法诞生之日起,其框架几乎没有发生变动,方法简单可靠,但“四阶段”技术依赖大规模的城市交通普查,在当今城市人口流动极其频繁的情况下,交通普查的成本和难度越来越大,其精度也不容乐观。同时,其传统预测模型难以反映社会发展,城市交通管理政策变化的影响,也无法考虑到周边环境随时间序列推移,对各交通小区出行的连锁反应。
1.2 研究内容
文章对交通拥堵进行判定,阐述交通拥堵产生的原因,收集了目前应对交通拥堵的方法,介绍了现有交通运行状况评价体系。同时,文章还对宏观交通仿真技术进行阐述,介绍了宏观交通仿真软件VISUM,提出了OD矩阵反推与交通预测模型相结合的思路。
研究以VISUM交通仿真软件上的Oppidum小镇为研究样本,将研究范围按用地情况和道路的自然分割划分为67个交通小区,查询得到的1960-2000年城市主干道年交通量。通过对1960-1999年数据分析处理,预测出2000年交通量。
2、宏观交通仿真机理
2.1 宏观交通仿真的定义
根据研究范围及对象的不同,交通仿真通常被分为宏观交通仿真、中观交通仿真和微观交通仿真 [2]。
宏观交通仿真要求采集路段速度和流量,相较于中观交通仿真和微观交通仿真,对交通实体、交通信号等细节要求比较低。在宏观交通仿真过程中,研究者以OD矩阵为主要研究对象,对交通基础设施建设和远景规划进行科学分析,如公交线路的优化、评价新建公路影响。
2.2 研究概况
交通仿真现状的发展分成三个阶段,20世纪60年代,研制了TRANSY、SIGOP等系统,但由于当时计算机发展不够好,仿真系统也并不完备。后来,随着计算机的发展,仿真模型迅速发展,出现了MISTRAN模型、SATURN宏观模型等[3]。到20世纪80年代,ITS的研究热潮袭来,各国相继研制了各种不同,应对不同情况和路段的仿真模型。到目前,交通仿真系统分为宏观和微观,微观的有CORSIM、PARAMICS和VISSIM,而宏观的有VISUM。传统的微观分析方法适用的范围、影响因素较小的情况,而宏观的交通仿真软件如VISUM以整体为目标,研究特定问题,分析路网情况,对交通流量进行分析分配,从而实现科学规划,减少拥堵情况。VISUM现已经用于对于路网的分析,为城市道路的规划提供依据[4]。
2.3 基于大数据交通仿真技术的城市交通量组合预测模型
交通仿真软件的出现在很大程度上促进了交通的发展,是交通领域的一座里程碑。随着社会的发展,影响交通的相关因素越来越多,应用计算机技术进行交通仿真就成为了一种很有效的技术手段。交通仿真不仅可以复现交通流时空变化的技术、为交通道路设计规划提供技术依据,而且还可以对各种参数进行比较和评价,以及环境影响的评价等。但是,交通是一个很复杂,又很巨大的一个体系,由于软件自身的局限性,往往在算法预测上不够精确,对交通状态的描述显得不够完善,因此,文章考虑将引入OD矩阵反推后的卡尔曼滤波模型应用于交通仿真软件VISUM,提出一种解决交通拥堵问题的新思路[5]。
3、卡尔曼滤波预测模型
3.1 模型提出背景
卡尔曼滤波是一种高效率的递归滤波器,是一种建立在最小方差估计的基础上的算法,利用线性系统状态方程,输入观测数据,再对系统进行最优估计。[6]
3.2 算法详述
将实际观察到的交通量数据,经过一系列运算反推出历史的OD矩阵,再运用卡尔曼滤波模型,运用方程对得到的OD矩阵进行处理,预测得到新的结果[7]。这样就将卡尔曼滤波模型与交通量结合起来,实现对OD矩阵的处理和运用。
以极大熵OD反推模型:

对于上述极大熵模型,由于其目标函数的特殊性,直接求解难以进行,通常用拉格朗日乘子法将其化为如下非线性方程组的形式:
上述方程组是含有M+1个变量和M+1个方程的非线性方程组,通过求解上述未知数即拉格朗日乘子,然后由(1)式求出OD矩阵,则有下式:
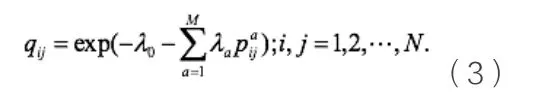
对于上述线性方程求解,采用数值解法。
4、现状交通分析
4.1 传统方法
卡尔曼滤波模型在交通需求预测中的应用,首先要根据交通流量时间和空间的相关性选择状态变量的个数。其基本有五个公式,简单介绍如下。
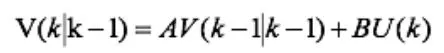
T表示协方差:
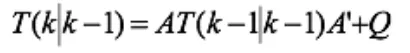
结合预测值和测量值,可以得到现在状态(k)的最优化估算值V(k|k) :

Kg为卡尔曼增益:
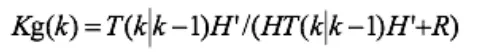
现在,得到了k状态下最优的估算值V(k|k)。为了使卡尔曼滤波器不断的运行下去直到系统过程结束,还要更新k状态下V(k|k) 的协方差即:
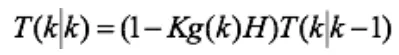
假设在k时刻某观察点的车辆数与k-1、k-2时间段都有一定关系和联系,根据这个关系,可以预测同一地点在k+1时刻的交通流[9]。
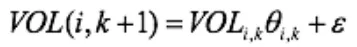
经过一系列处理和递推可以得到:
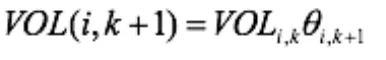
得到对比结果(图1):

图1 MATLAB图像
其中,红色为卡尔曼滤波,绿色为量测,蓝色为状态。得出根据卡尔曼滤波模型预测出的交通流量,再与实际流量对比,我们可以看出卡尔曼滤波模型对于预测的准确性和及时性情况[10]。通过加权计算绝对误差,我们发现预测值与实际值有10.56%的误差。
4.2 基于组合模型的交通分析
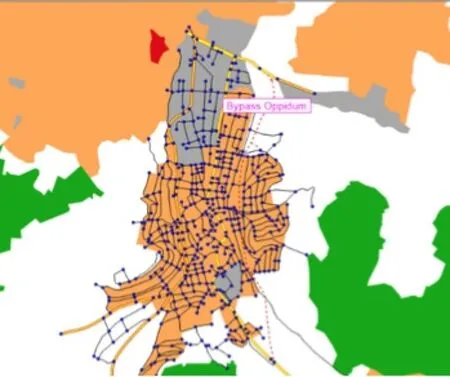
图2 Oppidum小镇路网图
在VISUM软件中,首先将Oppidum小镇分为67个交通小区(图2),并自动生成小区连接线,生成40个以极大熵OD反推模型为主要原理的OD反推矩阵,并存入数据库,接着,将1960-1999年的Oppidum小镇OD交通需求矩阵通过卡尔曼滤波交通需求预测,得出预测值,即2000年各路段交通量,与实际数据对比,通过加权平均算出绝对误差为5.11%。
4.3 传统四阶段法与组合模型的比较
与传统的"四阶段"技术相比,以极大熵原理为基础的OD反推算法与卡尔曼滤波模型相结合的方法的预测更加简便和高效。同时,与真实值相比,传统方法预测误差为10.56%,文中组合模型误差为5.11%,文中方法更加精确。
结论:
通过对传统交通流量需求预测四阶段法的改进,提出以历史交通流量基础,用VISUM软件中Oppidum小镇的数据,以极大熵模型反推出OD矩阵,再利用卡尔曼滤波模型对OD矩阵进行处理和预测,最后将预测出的OD矩阵输入VISUM仿真软件中进行重新分配。在新的预测方法中,将OD矩阵反推的极大熵模型和卡尔曼滤波模型结合起来,形成更优的组合模型,省去了传统方法中大量的交通调查,节省大量物力财力和时间,同时还提高了预测精度。本文提出的方法在精准性、可靠性、简便性、可行性方面都有一定优势,为今后更加有效的规划交通,更简便、精准的解决城市拥堵问题提供理论基础。
