落矿冲击作用下矿柱结构参数优化与稳定性分析

于清军，李元辉，刘照朋，纪晓飞，彭康



落矿冲击作用下矿柱结构参数优化与稳定性分析

于清军1, 2，李元辉1，刘照朋3，纪晓飞2，彭康3

(1. 东北大学 资源与土木工程学院，辽宁 沈阳，110819；2. 赤峰山金红岭有色矿业有限责任公司，内蒙古 赤峰，025450；3. 重庆大学 煤矿灾害动力学与控制国家重点实验室，重庆，400044)

应用理论计算和ABAQUS数值模拟软件对6种桃形矿柱稳定性进行分析。首先，将开采中段划分为4个盘区进行开采；其次，基于结构力学模型，分析6种桃形矿柱参数对巷道在最大冲击力下的最小保护层厚度变化的影响；最后，对桃形矿柱在冲击作用下的巷道残余完整长度与垂高分别进行筛选，并选择桃形矿柱最佳设计方案。研究结果表明：在回采过程中，开采中段顶板受力状态由压应力变为拉应力，间柱压力增大，但顶板和间柱均稳定，未达到破坏强度；桃形矿柱坡度越大，保护层厚度越小；在冲击载荷作用下，坡度越小的桃形矿柱受破坏程度越小，高度越大的矿柱变形能越大；桃形矿柱坡角为 60°、总高为15 m的方案为最佳设计方案。

桃形矿柱；冲击荷载；数值模拟；稳定性分析

目前，急倾斜极厚大矿体开采以崩落采矿法为主，该方法采出矿量占金属矿床开采总量50.0%以上。但该采矿法在开采中存在诸如矿石贫损大、空区下作业安全性差等问题[1−2]。针对采空区稳定性问题，宫凤强等[3]考虑影响采空区稳定性的14项因素，建立各影响因素的未确知测度函数并对采空区危险性进行评价。PENG等[4−5]利用数值模拟与理论模型对海下矿体安全开采的隔离层厚度进行了研究。李文秀等[6−7]利用模糊数学理论得出地下矿体开采引发的岩体移动变形及上部边坡稳定性规律。赵海军等[8]采用数值软件方法对高构造应力矿体开采的岩移规律与变形机理进行了分析。这些研究大多针对采场顶板的稳定性进行分析，对采场范围内的岩石滚落、崩塌及爆破落矿等冲击载荷分析较少。围岩崩塌具有分布广泛、突发性、致灾严重、灾前迹象不明的特点，因此，其防治难度更大。岩石冲击对顶板稳定性的影响可以归结于结构的撞击。撞击理论的演化主要有4个方面：基于脉冲−动量定理的经典力学、弹性应力波传播、接触力学和塑性理论。不同的撞击理论适用于不同撞击特性：脉 冲−动量定理方法能够求解回弹速度，但不能确定冲击力；波传播理论可以得到撞击物内的应力，但动力分析中的积分计算过程比较复杂；接触力学方法把接触区域作为弹簧−阻尼系统，把撞击问题作为连续时间动力问题处理；塑性理论仅适用于高速撞击问题。宫凤强等[9]对花岗岩试样进行“静态—准静态—动态”范围内的压缩试验，获得压缩强度、峰值应变和切线模量随撞击速度增大的变化规律。杨其新等[10]基于室内试验建立落石冲击力计算方法。何思明[11]基于落石冲击力试验结果和HERTZ弹性碰撞理论推导出落石自由落体情形下的最大冲击力计算公式。此外，应用数值模拟方法也可以很好地解决冲击碰撞问题。DELHOMME等[12]运用ANSYS软件分析了棚洞在不同落石冲击作用下的动力响应和内力分布。而在地下开采中，岩石可以视为刚性结构，落石砸在顶板上的瞬间会产生巨大的冲击力，这个冲击力往往是落石自身质量的数十倍甚至上百倍，严重威胁开采安全。在红岭矿实际生产中，当形成具有底部出矿结构的桃形矿柱后，桃形矿柱上方0～27.5 m高度范围内将掉落大量矿石。在矿石的冲击作用下，桃形矿柱结构的稳定性与完整性将直接影响采矿生产的安全性和经济效益。因此，本文作者以红岭矿五中段某矿房为研究对象，对冲击荷载下桃形矿柱的稳定性进行研究，以期在确保生产安全前提下提高出矿量。

1 工程概况

1.1 矿区概况

目前红岭矿的综合采选能力已达5 000 t/d，矿区是以铅、锌为主的矽卡岩型多金属矿床，矿体平均走向长为1 350 m，平均倾角为75°，矿区围岩有矽卡岩、板岩和大理岩，上、下盘围岩及矿体均较稳固。矿区地质构造与区域地质构造线基本一致，以北东向构造为主，根据矿山资料和区域水文地质资料综合分析，矿区基岩裂隙含水层分布普遍，基岩裂隙含水层单位涌水量为0.003 2 L/(s·m)，属弱含水层，矿区地质模型示意图见图1。本文研究的4117采场位于1号矿体的17线至19线之间，矿体平均倾角为75°，标高为805~ 863 m。

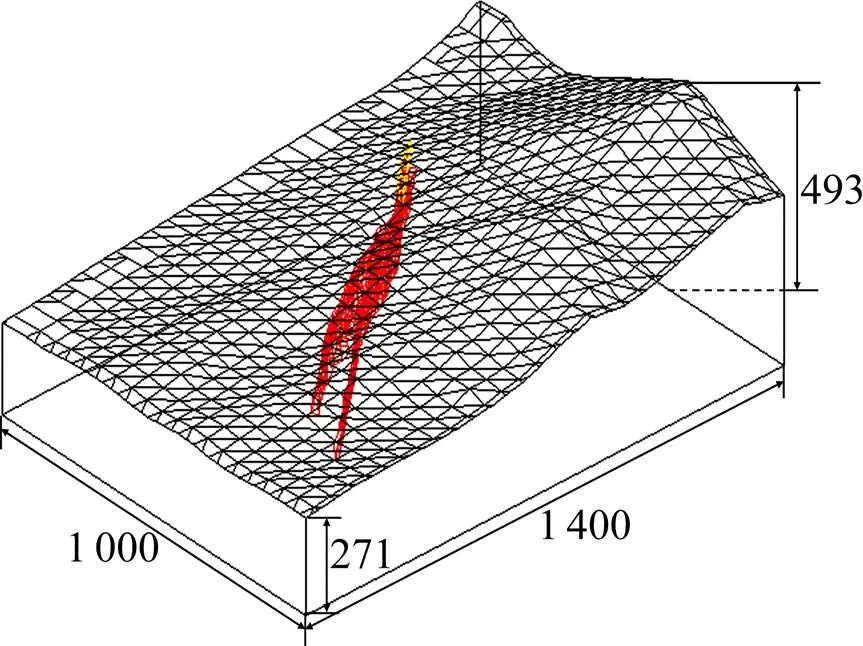
数据单位：m

1.2 岩石力学基础实验

红岭矿区矿体及围岩的块度较大，一般较致密坚硬，稳固性较好。矿区矿体上盘为板岩、矽卡岩，矿体下盘为大理岩或矽卡岩。经现场勘查并取样进行室内实验，抗压试验采用YE4−100型液压式压力试验机，最大载荷为100 t，采用应力传感器UCOM−60A静态采集仪对岩石所加荷载和横、纵向变形进行测量，得到岩石的抗压强度、弹性模量和泊松比。剪切试验采用YAW−300微机控制电液伺服岩体直剪试验机，测量岩石的抗剪强度、内聚力和内摩擦角，通过劈裂拉伸试验测量岩石的抗拉强度。矿岩力学特性如表1所示。

1.3 矿区地应力规律

红岭矿区水平构造应力主应力(hmax)方向垂直矿体走向，最小主应力(hmin)方向沿矿体走向，地应力场各主应力随埋深变化的规律如下：

hmax=0.026+10.008 (1)

hmin=0.023+1.802 (2)

z=0.026+1.812 (3)

式中：z为竖直方向的应力；为竖直方向深度。

通过现场应力的测量和计算分析可知红岭矿区最大主应力的走向为北西向。从地应力测量结果可知：红岭地区最大水平主应力方位一致性较好，均为北东方向，且均为近水平向的压应力。矿区的主要地质构造以北东向为主，最大主应力方向大致平行于构造走向，地应力明显受构造作用的影响。

1.4 采矿工艺

红岭铅锌矿现阶段选用盘区阶段空场崩落联合采矿法，矿块长为50 m，其中矿房长为32 m，间柱长为18 m。以矿体厚度为矿块宽，约为40 m，顶柱厚为10 m，阶段高为50 m。矿房采用空场法回采，间柱和顶柱则采用崩落法回采。根据红岭矿现场采矿方法的具体参数，利用3DMine，3DsMax和VRP(virtual reality platform)等三维建模软件，结合五中段某采场的矿体赋存情况，制作出1个盘区的采准、切割、回采的全部工艺流程，使该采矿方法的结构参数、工艺流程、工艺特点等通过动画形式立体呈现出来。矿房结构参数导入VRP后的部分矿房回采工艺动画模型如图2所示。该回采过程包括采准前中的巷道掘进，切割工程中的切割拉底、切顶等工作。矿柱回采工艺动画模型如图3所示。一套完整矿柱回采工艺包括在顶部矿柱钻孔、爆破、落矿等。

2 中段矿柱稳定性分析

图4所示为中段矿柱开采示意图。由图4可见：整个中段矿柱回采分为4个盘区进行，由中部依次向两翼回采。图5所示为中段矿柱测线位置及矿房编号。图5中，测线为顶板下表面沿着矿体走向选取的1条沿顶板的曲线，由此可知该线上不同盘区回采过程中矿房应力变化情况。

表2所示为盘区开采过程中回采顶板及间柱应力变化，开采过程中各顶板间柱应力变化如图6所示。由表2可知：当回采第1盘区时，应力集中区域为 4104空区顶板，最小主应力由回采前的−1.75 MPa变为0.74 MPa，压应力变为拉应力；最大主应力由回采前的−6.60 MPa变为−16.20 MPa，压应力增大。当回采第2盘区时，应力集中区域为4104空区顶板与4100右侧间柱；4104空区顶板的最大主应力由回采前的 −16.20 MPa变为−4.20 MPa，压应力减小；4100右侧间柱最大主应力由回采前的−3.60 MPa变为−9.60 MPa，压应力增大。当回采第3盘区时，应力集中区域为4110左侧间柱与4109左侧间柱；4110左侧间柱最大主应力由回采前的−8.00 MPa变为−3.60 MPa；4109左侧间柱最大主应力由回采前的−9.60 MPa变为−3.90 MPa，压应力减小。当回采第4盘区时，应力集中区域为41-2间柱右侧与4100右侧间柱；41-2间柱右侧最大主应力由回采前的−10.00 MPa变为−2.75 MPa；4100右 侧间柱最大主应力由回采前的−9.68 MPa变为 −2.53 MPa，压应力减小。在4个盘区回采过程中，顶板与间柱最小主应力表现为由压应力向拉应力过渡，最大主应力表现为压应力增大。在4个盘区回采完毕后，整个中段矿柱最大压应力与拉应力均在安全应力范围内，不发生破坏。

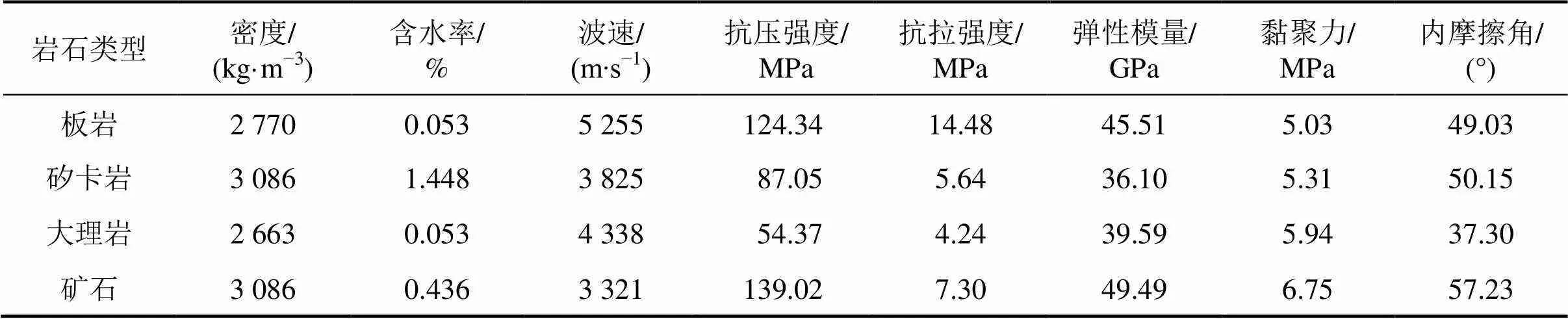
表1 矿岩力学特性

(a) 采准过程；(b) 切割拉底；(c) 切顶

(a) 采准；(b) 爆破；(c) 落矿

图4 中段矿柱回采示意图

图5 中段矿柱测线位置及矿房编号

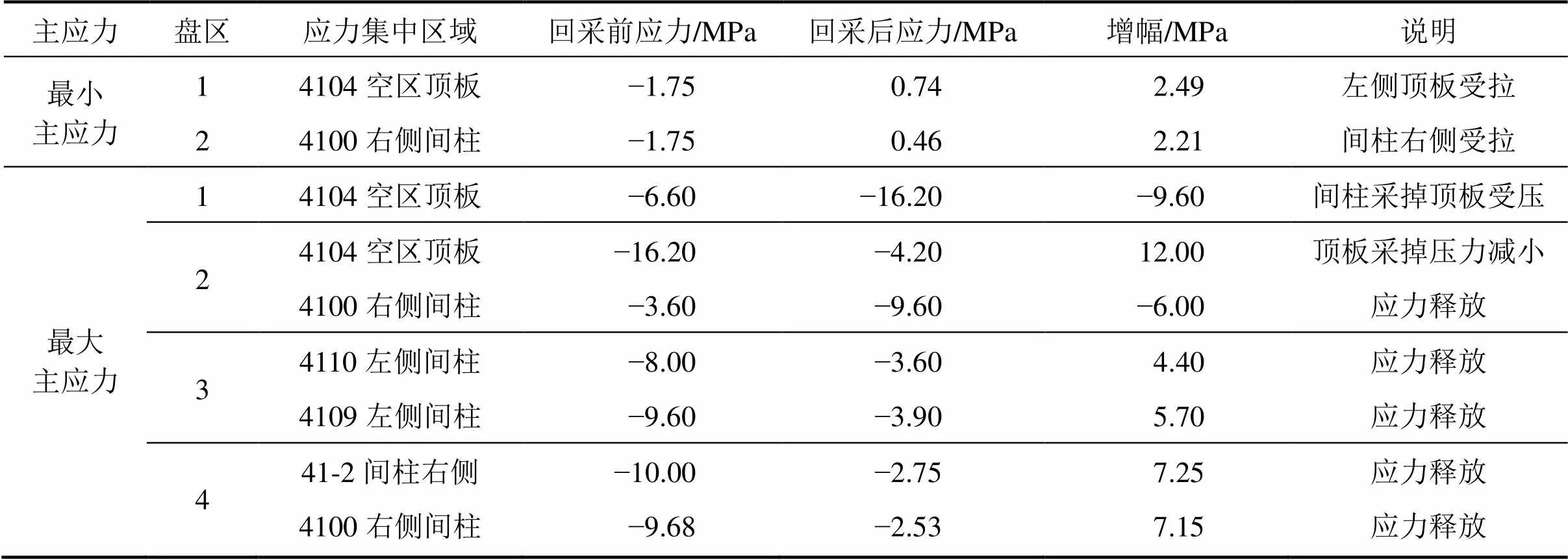
表2 中段矿柱回采前后顶板及间柱应力变化

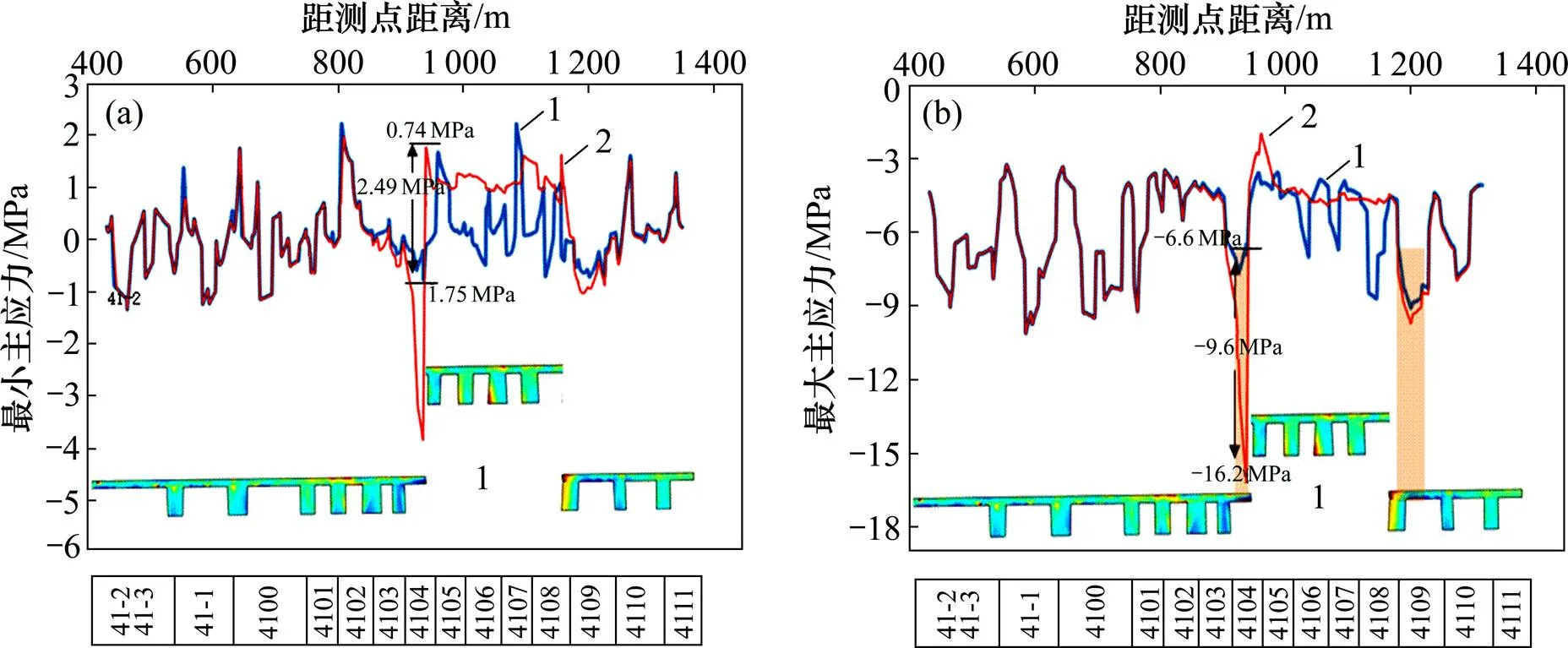
(a) 最小主应力；(b) 最大主应力

3 矿柱稳定性分析

根据矿区采矿方法特点，桃形矿柱上方0~27.5 m范围掉落大量矿石，将对桃形矿柱产生数倍于自身重力的冲击力，在冲击作用下桃形矿柱将产生一定程度破坏，从而影响桃形矿柱保护范围内运输巷道结构的稳定性与完整性。对于冲击问题，本文采用球体碰撞问题来分析。设崩落矿石与桃形矿柱质量分别为1和2，半径为1和2，弹性模量为1和2，泊松比为1和2，碰撞前矿石对应的速度为1，碰撞后矿石法向速度为2。碰撞过程可分为2个阶段：从接触开始至相对速度减为0 m/s，这个过程称为压缩阶段；随后2个物体开始恢复变形至2个物体分离，这个过程称为恢复阶段。根据Hertz理论，2个物体发生碰撞时，压缩阶段所需时间1及恢复阶段所需时间2分别为：

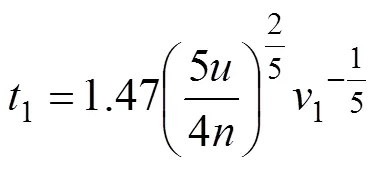
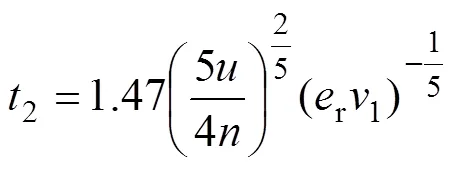
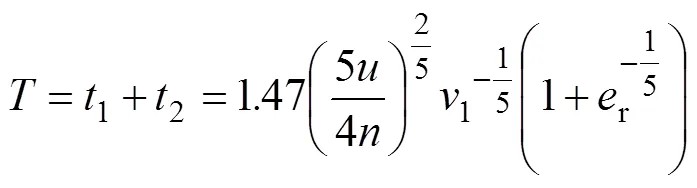
式中：为碰撞过程接触总时间；为接触刚度系 数，;为质量交换系数，=；1和2为钢球材料有关的参数，1=，2=；r为碰撞恢复系数，r=2/1。

碰撞恢复系数应用广泛，目前碰撞恢复系数暂无统一定义，大都通过现场试验或根据经验获取，本文采用基于准静态接触力学理论的法向恢复系数计算公式来对冲击力进行求解[13]：

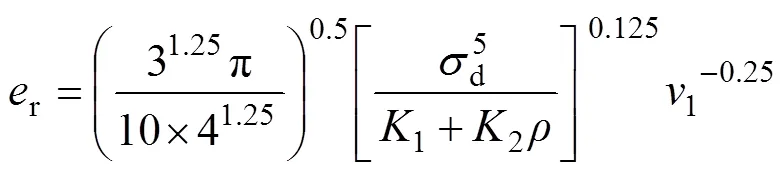
式中：d为缓冲岩体的屈服应力；为落石密度。

相关研究表明，落石冲撞过程中，冲击力随时间变化的曲线可近似表示为正弦或余弦函数。最大冲击力max的计算公式为

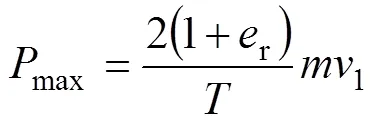
根据该采矿方法中桃形矿柱设计参数，建立桃形矿柱立体模型，如图7所示，6种桃形矿柱方案参数如表3所示。

根据6种桃形矿柱设计参数，爆破后现场岩石破碎情况，选取边长为0.5 m的立方体矿石为冲击矿体。结合式(4)~(8)计算得到崩落矿体撞击在桃形矿产生的最大冲击力max(见表3)。

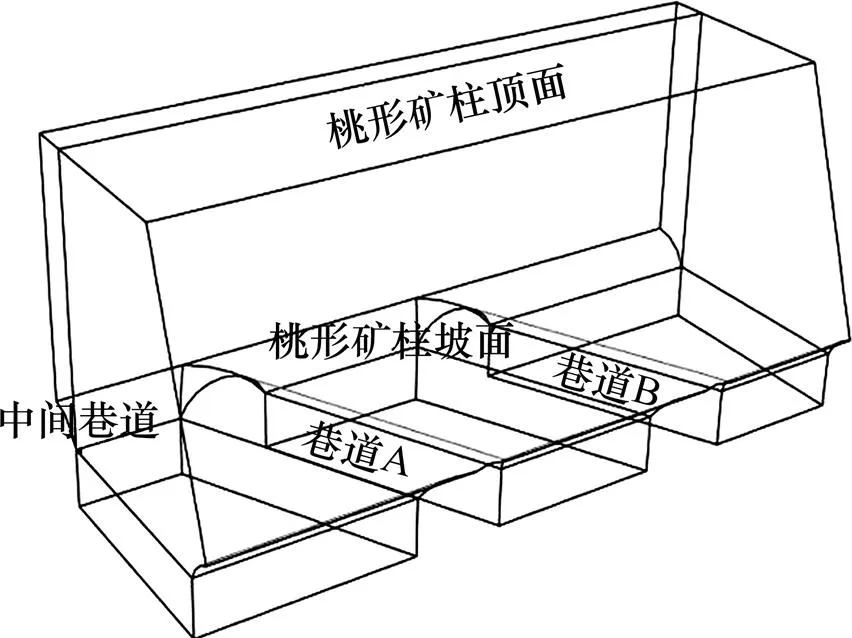
图7 桃形矿柱模型示意图

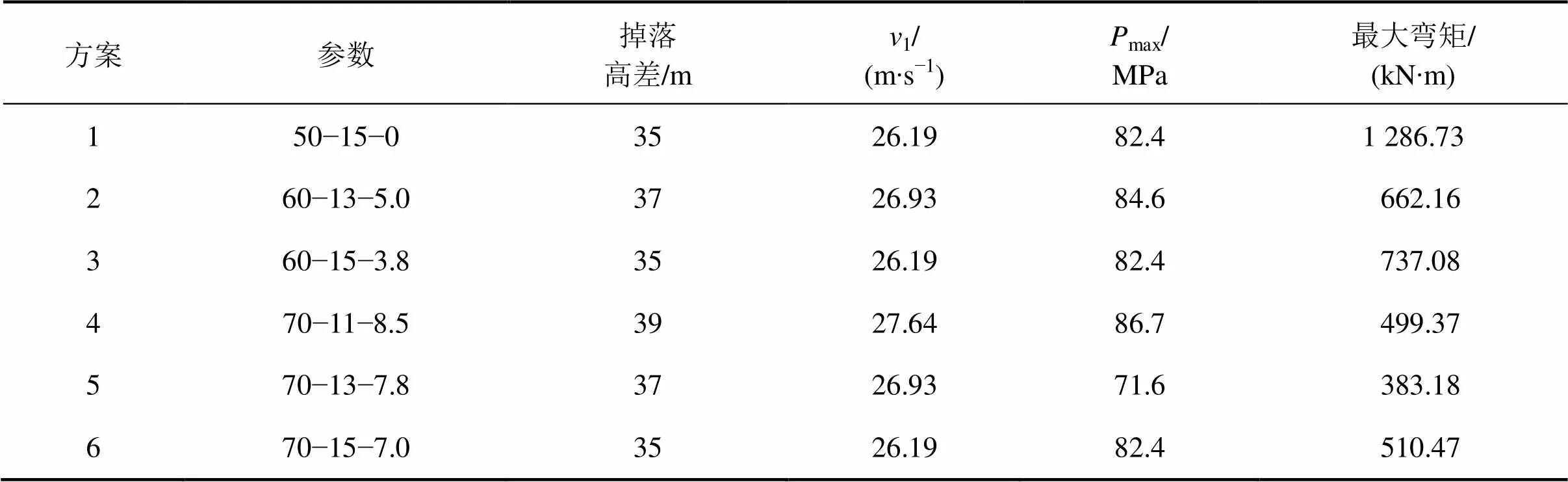
表3 6种桃形矿柱方案的参数

注：参数50−15−0表示桃形矿柱坡角为50°，总高度为15 m，平台高度为0 m。

爆破后的矿石将冲击在桃形矿柱表面，各桃形矿柱受力简化模型如图8所示(其中为矿柱坡角)。由图8可知：对桃形矿柱斜面上的力进行分解，即可求得垂直于斜面的作用力。根据该模型对桃形矿柱进行受力分析，选取矩形截面单元，采用材料力学计算公式计算矿柱受力情况：

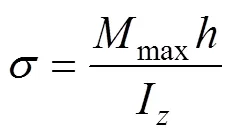
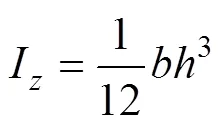
式中：为矿柱截面边界点压应力；max为截面受力最大弯矩；I为矿柱截面惯性矩；为矩形截面宽度，取=1 m。

利用式(9)和(10)，取为矿柱极限抗拉强度，即可求得各方案中最小保护层厚度分别为3.55，3.31，3.49，2.87，2.52和2.91 m。由此可见，桃形矿柱坡度越大，保护层厚度越小。

4 矿柱稳定性分析数值模拟

4.1 数值模拟及分析过程

有限元分析采用4步骤模拟的方式[14−18]，数值模拟步骤及分析过程如下：1) 将崩落的矿体定义为具有一定块度的均匀块体，块体自由落体冲击桃形矿柱的顶面和坡面；2) 获得桃形矿柱表面与块体的接触应力时程；3) 将接触应力时程作为动力荷载，均匀施加于桃形矿柱表面；4) 获得动力作用下桃形矿柱弹塑性模型的动力学响应。在这个过程中，由于块体冲击矿柱时是不均匀的，因此，在表面选取足够多的点，再取表面接触应力平均值作为后续施加的荷载。

4.2 矿柱位移响应规律

图9所示为各方案中冲击应力达到峰值时矿柱的位移云图和破坏后最终形貌。由于各方案中冲击应力达到峰值时的矿柱瞬时位移响应和最终稳定状态的矿柱位移响应不同，故本次位移选取合位移。由图9可见：由于方案1没有顶部平台，崩落体全部砸在坡面上，最大位移发生范围主要集中在斜坡坡脚处。其他方案由于存在顶部平台，部分矿体冲击在顶部平台上，使得顶部平台和矿体发生正面冲击，因此，顶部平台位移比坡面位移更大一些。

本文以位移为15 cm为界线，给出矿柱内部位移达到15 cm的分界面(见图9)。分界面可近似认为是崩落体冲击后桃形矿柱最终的表面形貌。对桃形矿柱最终形态的位移云图分析可知：方案1的破坏主要发生在坡角处；方案3除坡角有损坏外，在自由端的顶部有砸坏现象；方案5和方案6都有大范围破坏的情况，且破坏程度远比坡度为60°和50°的方案的高。位移分析结果表明：坡面对冲击载荷有很大的缓冲作用，可在很大程度上改善桃形矿柱的受力状态，且坡度越小，桃形矿柱受破坏的范围和程度也越小。

4.3 矿柱应力应变响应规律

图10所示为不同方案中矿柱在冲击载荷后的内部应力分布图，该应力为等效Mises偏应力，表示材料的单位体积形状改变的弹性位能，该应力可以判断岩土体形变能。由图10可见：受力状态最好的是方案1，该方案中矿柱内部巷道处的Mises应力最小。该方案形变能集中主要分布在桃形矿柱内部的巷道处。其他方案中形变能主要集中内部巷道与内部岩体中，这是因为其他方案中都存在顶部平台，崩落矿体冲击在顶部平台上发生正碰，造成矿体内部形变能集中。在6个方案中，随着桃形矿柱的高度变大，冲击距离减小，冲击力减小，应力反而变大。这是由于桃形矿柱体积增大，使得形变能有更多的载体，传递到内部巷道处的变形能也越大。随着坡度增大，桃形矿柱的形变能越来越大。

图11所示为不同方案中矿柱等效塑性应变分布图。在ABAQUS数值模拟软件中，以第一主应变为指标，最大主应变为正表明材料处于受拉状态。对于该桃形矿柱而言，在受到矿石冲击后应力释放的过程中，矿柱表面和内部有伸张的情况发生，这与其裂缝的产生和闭合裂缝的张开有密切关系。由图11可知：几种方案中矿柱应变最终状态均为正值，表明矿柱均处于受拉状态，矿柱极易在这种状态下发生拉伸破坏。同时，各个方案中矿柱几乎都进入了塑性阶段，其中方案1中矿柱的塑性发展最小，而其他方案中，随着桃形矿柱的高度变大，矿柱内部和底部处的塑性变形减小，这是由于矿柱较高时崩落体掉落的距离更短，导致冲击荷载减小。方案1中应变集中发生在坡脚处；方案2和3中应变集中在坡面处，且在坡面分布较为均匀；方案4，5和6中主体应变更大，主体破坏严重。上述分析结果也表明桃形矿柱坡角为60°时对崩落的矿石有更好的缓冲作用，从而避免矿柱产生拉伸裂隙而失稳破坏。

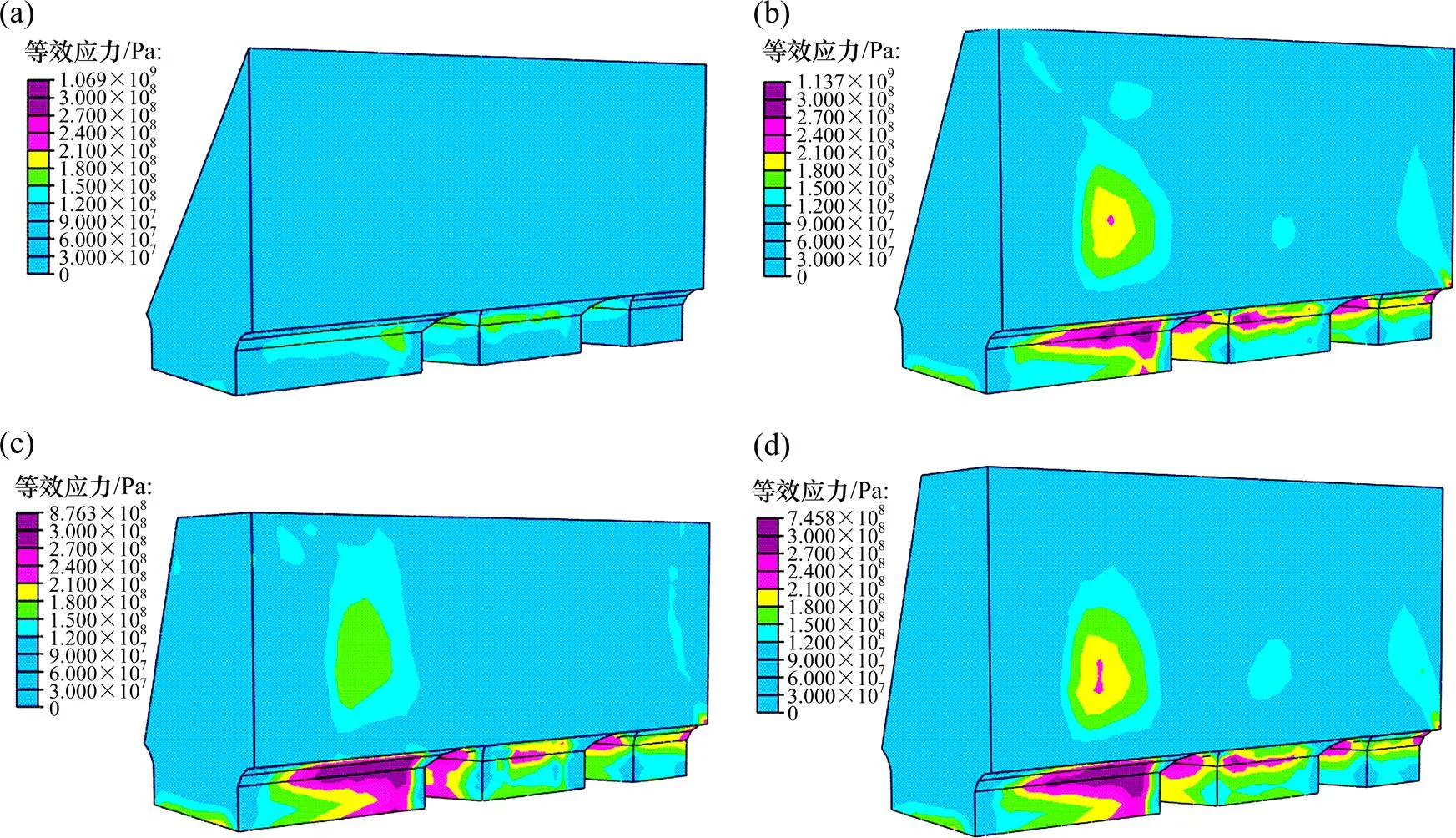
(a) 方案1; (b) 方案3; (c) 方案5; (d) 方案6

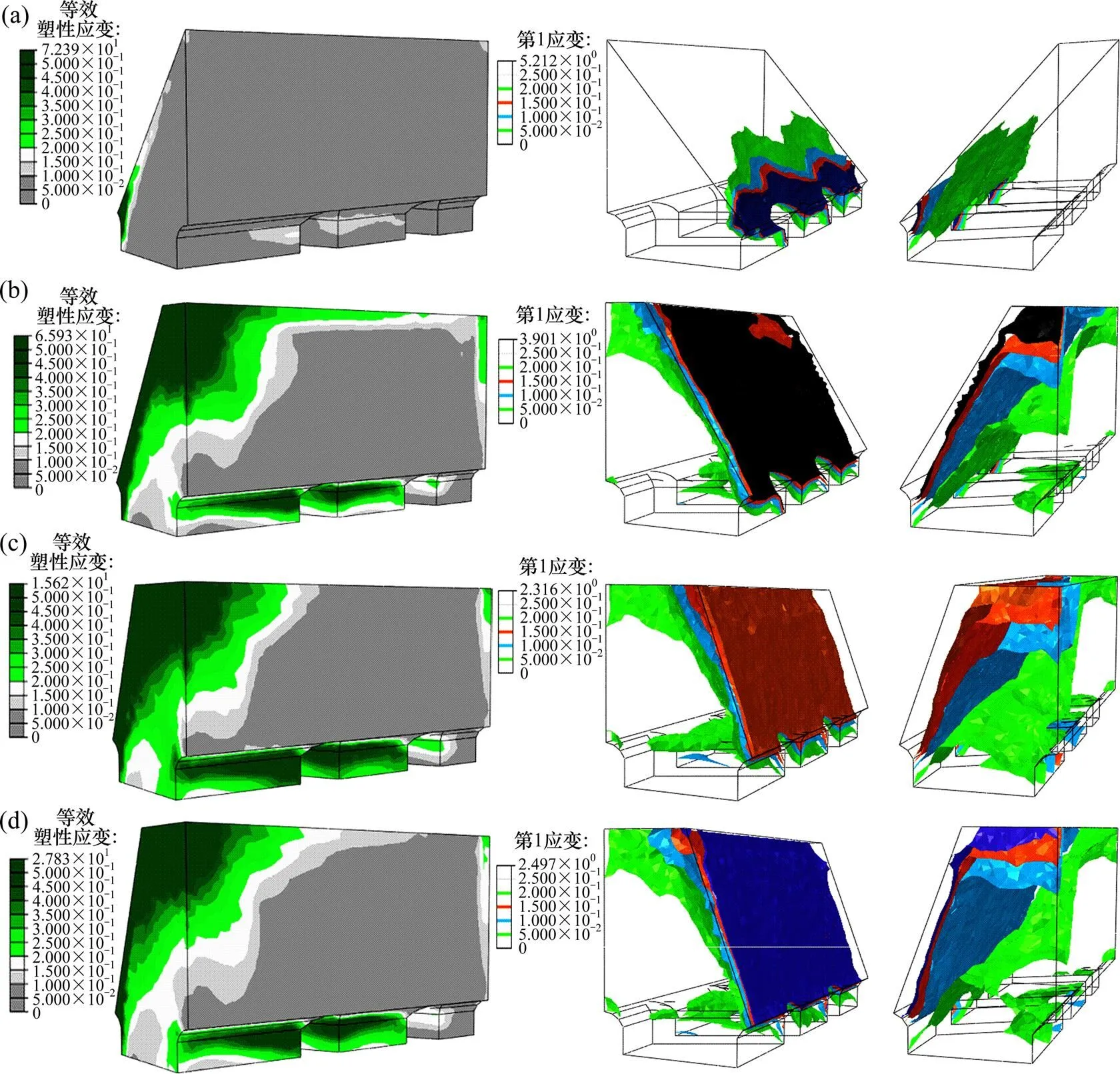
(a) 方案1; (b) 方案3; (c) 方案5; (d) 方案6

4.4 残余完整巷道长度与垂高

为进一步确定桃形矿柱结构的最佳参数，从底部出矿结构的安全性和完整性角度分析，选择残余完整巷道长度与垂高2个指标进行研究。残余完整巷道长度与垂高示意图如图12所示。

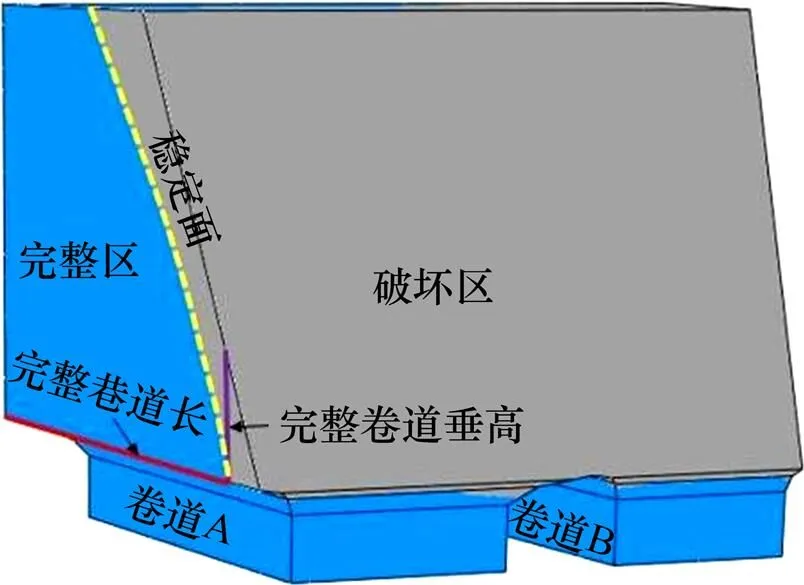
图12 残余完整巷道长度与垂高示意图

假设在落矿冲击作用下该巷道位移小于15 cm，则定义该巷道为完整巷道。6种桃形矿柱方案在受崩落矿石冲击后，沿巷道长度方向各点的位移如图13所示。不同方案中A和B巷道的残余完整巷道长度与垂高对比如表4所示。

由表4可知：方案1中A和B这2个巷道的垂高最小，均不足2.00 m，完整巷道长度分别为8.65 m和8.55 m。方案2中A和B巷道的完整巷道长度最大，分别达到9.11 m和9.16 m，垂高仅有2.30 m和 2.22 m，仅高于方案1中的巷道垂高。方案3巷道垂高达到3.56 m和3.89 m，但完整巷道长度较短，为8.34 m和8.14 m。对于方案4~6，随桃形矿柱高度增大，完整巷道长度也逐渐增大，但巷道垂高则逐渐减小。这是由于矿柱较高方案中崩落矿体掉落距离较短，作用于桃形矿柱表面的冲击荷载较小，对底部出矿结构的破坏也较小，完整巷道长度则较大。此外，随高度增加，桃形矿柱体积也在增大，应变能有更多载体，传递到内部巷道的能量也较多，使得完整巷道的垂高逐渐减小。结合本文第3节中的计算结果可知：在最大冲击力下，方案1~6中巷道最小保护层厚度分别为3.55，3.31，3.49，2.87，2.52和2.91 m。在巷道完整垂高参数选择中，方案1和方案2的完整巷道垂高均小于最小保护层厚度，不符合条件；方案3~6的完整巷道垂高均满足最小保护层厚度要求。在巷道完整长度参数选择中，方案3巷道完整长度总和最长，优选方案3作为最佳设计方案。 综合上述分析，从桃形矿柱出矿的安全、高效等角度考虑，优选坡面角度为60°，高度为15 m为桃形矿柱的最佳设计参数。

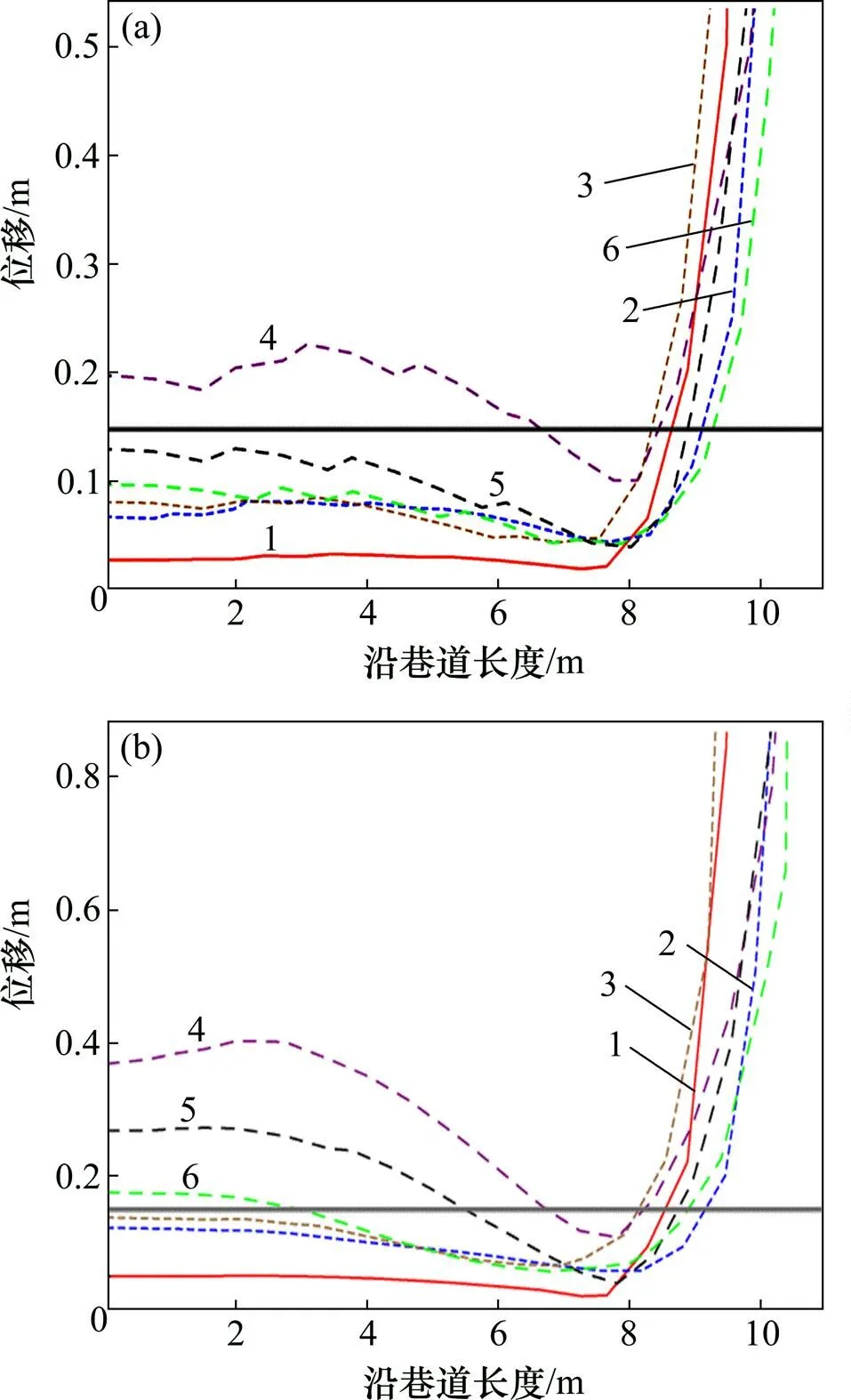
(a) A巷道; (b) B巷道

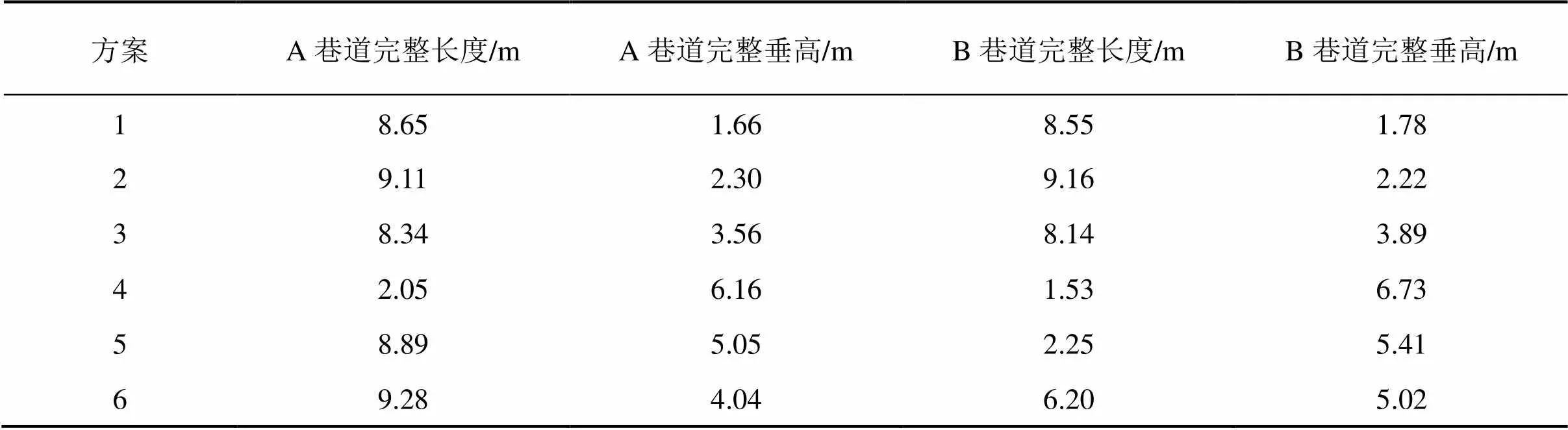
表4 不同方案中残余完整巷道长度与垂高对比

4.5 落矿下盘顶板位移监测

红岭矿区采用多点位移计对顶板变形进行监测。多点位移计是由多支智能型位移计、传递杆、锚头等组成。位移计本体内有1个圆柱形金属螺旋线圈，线圈内有1个可以移动的磁芯(即测杆)，在实际应用中，通过线圈的电感变化实现非电量电测。

在工程施工过程中，根据实际情况，位移观测线选择在下一中段各个矿房的顶板，研究上一中段矿石崩落后对该中段各矿房顶板竖向沉降变形的影响。

传感器位移收敛信号从上一中段矿柱爆破前开始对顶板位移进行监测，爆破矿柱完成30 d后，收集各矿房测得的位移变化，如图14所示。从图14可以看出：开采前后各矿房顶板位移变化较小，其中顶板16号监测点顶板沉降位移最大，为3.42 mm，整个中段顶板位移均小于4 mm，表明上一中段落矿冲击后，下一中段的开采是安全的。

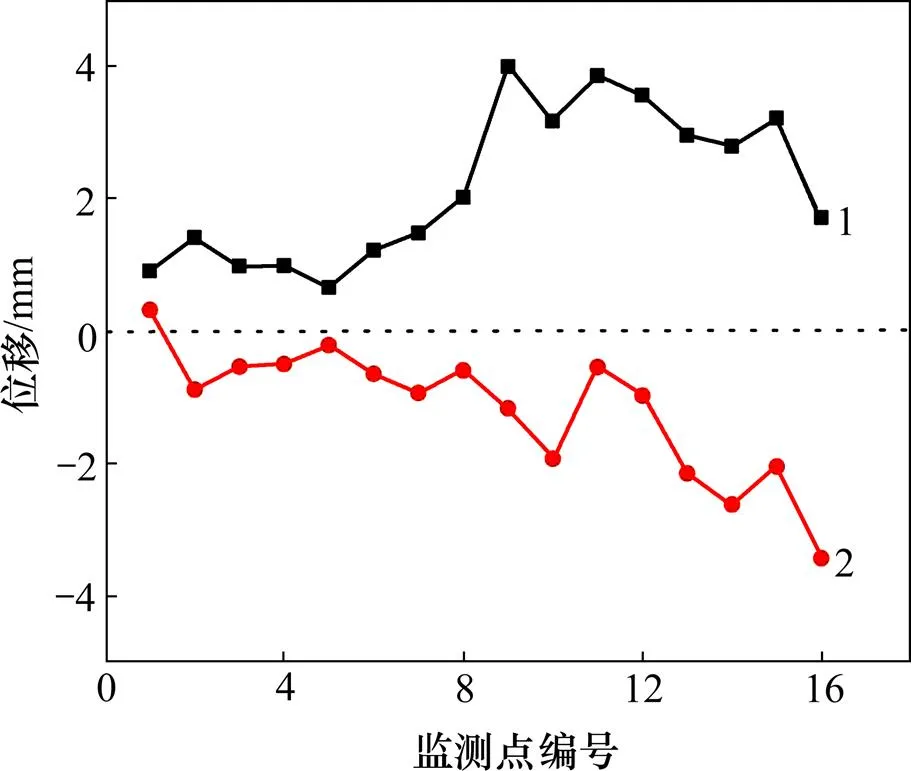
1—回采前；2—回采后。

5 结论

1) 在矿柱回采过程中，开采中段顶板受力状态由压应力变为拉应力，间柱压力增大，但顶板和间柱均稳定，未达到破坏强度。

2) 桃形矿柱坡度和高度越大，巷道最小保护层厚度越小。

3) 桃形矿柱在冲击载荷作用下，坡度越小的桃形矿柱受破坏程度越小，高度越大冲击力越小，桃形矿柱变形能越大。

4) 选择方案3(坡角为60°，总高为15 m)为桃形矿柱最佳设计方案，开采过程中下一中段顶板和间柱的应力及位移变化均较小，符合安全生产要求。

[1] 陶干强, 刘振东, 任凤玉, 等. 无底柱分段崩落法采场结构参数优化研究[J]. 煤炭学报, 2010, 35(8): 1269−1272.

TAO Ganqiang, LIU Zhendong, REN Fengyu, et al. Optimization research of stope structural parameters in sublevel caving with non-pillar[J]. Journal of China Coal Society, 2010, 35(8): 1269−1272.

[2] 袁仁茂, 马凤山, 邓清海, 等. 急倾斜厚大金属矿山地下开挖岩移发生机理[J]. 中国地质灾害与防治学报, 2008, 19(1): 62−67.

YUAN Renmao, MA Fengshan, DENG Qinghai, et al. Mechanism of ground movement induced by underground mining of metal deposit with steep occurrence and large thickness[J]. The Chinese Journal of Geological Hazard and Control, 2008, 19(1): 62−67.

[3] 宫凤强, 李夕兵, 董陇军, 等. 基于未确知测度理论的采空区危险性评价研究[J]. 岩石力学与工程学報, 2008, 27(2): 323− 330.

GONG Fengqiang, LI Xibing, DONG Longjun, et al. Underground goaf risk evaluation based on based on uncertainty measurement theory[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(2): 323−330.

[4] PENG Kang, LIU Zhaopeng, ZHANG Yongliang, e t al. Determination of isolation layer thickness for undersea mine based on differential cubature solution to irregular Mindlin plate[J]. Journal of Central South University, 2017, 24(3): 708−719.

[5] 李夕兵, 刘志祥, 彭康, 等. 金属矿滨海基岩开采岩石力学理论与实践[J]. 岩石力学与工程学报, 2010, 29(10): 1945−1953.

LI Xibing, LIU Zhixiang, PENG Kang, et al. Theory and practice of rock mechanics related to exploitation of undersea metal mine[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(10): 1945−1953.

[6] 李文秀. 急倾斜厚大矿体地下与露天联合开采岩体移动分析的模糊数学模型 [J]. 岩石力学与工程学报, 2004, 23(4): 572−577.

LI Wenxiu. Fuzzy mathematics models on rockmass displacements due to open-underground combined mining for thick ore body with steep dip angle [J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(4): 572−577.

[7] 李文秀, 王山山, 刘琳, 等. 官庄铁矿深埋破碎矿体开采岩体变形测试分析[J]. 岩石力学与工程学报, 2010, 29(4): 681−688.

LI Wenxiu, WANG Shanshan, LIU Lin, et al. Measurement analyses of rock mass movement and deformation due to underground mining of deep fractured orebody in Guanzhuang iron mine[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(4): 681−688.

[8] 赵海军, 马凤山, 丁德民, 等. 急倾斜矿体开采岩体移动规律与变形机理[J]. 中南大学学报(自然科学版), 2009, 40(5): 1423−1429.

ZHAO Haijun, MA Fengshan, DING Demin, et al. Law of ground movement and its deformation mechanism induced by mining steep deposit[J]. Journal of Central South University (Science and Technology), 2009, 40(5): 1423−1429.

[9] 宫凤强, 王进, 李夕兵. 岩石压缩特性的率效应与动态增强因子统一模型[J]. 岩石力学与工程学报, 2018, 37(7): 1586−1595.

GONG Fengqiang, WANG Jin, LI Xibing. The rate effect of compression characteristics and a unified model of dynamic increasing factor for rock materials[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(7): 1586−1595.

[10] 杨其新, 关宝树. 落石冲击力计算方法的试验研究[J]. 铁道学报, 1996, 18(1): 101−106.

YANG Qixin, GUAN Baoshu. Test and research on calculating method of falling in stone impulsive force[J]. Journal of the China Railway Society, 1996, 18(1): 101−106.

[11] . 滚石对防护结构的冲击压力计算[J]. 工程力学, 2010, 27(9): 175−180.

HE Siming. Calculation of compact pressure of rock-fall on shield structures[J]. Engineering Mechanics, 2010, 27(9): 175−180.

[12] DELHOMME F, MOMMESSIN M, MOUGIN J P, et al. Simulation of a block impacting a reinforced concrete slab with a finite element model and a mass-spring system[J]. Engineering Structures, 2007, 29(11): 2844−2852.

[13] 刘涌江. 大型高速岩质滑坡流体化理论研究[D]. 成都:西南交通大学土木工程学院, 2002: 58−62.

LIU Yongjiang. Study on fluidifying theory of large high speed rockslide[D]. Chengdu: Southwest Jiaotong University. College of Civil Engineering, 2002: 58−62.

[14] 潘晓明, 孔娟, 杨钊, 等. 统一弹塑性本构模型在ABAQUS中的开发与应用[J]. 岩土力学, 2010, 31(4): 1092−1098.

PAN Xiaoming, KONG Juan, YANG Zhao, et al. Secondary development and application of unified elastoplastic constitutive model to ABAQUS[J]. Rock and Soil Mechanics, 2010, 31(4): 1092−1098.

[15] 邓楚键, 何国杰, 郑颖人. 基于M-C准则的D-P系列准则在岩土工程中的应用研究[J]. 岩土工程学报, 2006, 28(6): 735−739.

DENG Chujian, HE Guojie, ZHENG Yingren. Studies on Drucker-Prager yield criterions based on M-C yield criterion and application in geotechnical engineering[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(6): 735−739.

[16] 楚锡华, 徐远杰, 孔科. M-C与D-P屈服准则计算参数的能量等效方法及误差分析[J]. 岩石力学与工程学报, 2009, 28(8): 1666−1673.

CHU Xihua, XU Yuanjie, KONG Ke. Energy equivalent method for calculating parameters of M-C and D-P criteria and error analysis[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(8): 1666−1673.

[17] 楚锡华, 徐远杰. 基于形状改变比能对M-C准则与D-P系列准则匹配关系的研究[J]. 岩土力学, 2009, 30(10): 2985−2990.

CHU Xihua, XU Yuanjie. Studies on transformation from M-C criterion to Drucker-Prager criterions based on distortion energy density[J]. Rock and Soil Mechanics, 2009, 30(10): 2985−2990.

[18] 朱向荣, 王金昌. ABAQUS软件中部分土模型简介及其工程应用[J]. 岩土力学, 2004, 25(增刊2): 144−148. ZHU Xiangrong, WANG Jinchang. Introduction to partly soil models in ABAQUS software and their application to the geotechnical engineering[J]. Rock and Soil Mechanics, 2004, 25(S2): 144−148.

Stability analysis and structural parameter optimization of pillar under impact of rockfall

Yu Qingjun1, 2,Li Yuanhui1,Liu Zhaopeng3,Ji Xiaofei2,Peng Kang3

(1. College of Resources and Civil Engineering, Northeastern University, Shenyang 110819, China; 2. Chifeng Jinhong Mountain Non-ferrous Mining Co. Ltd., Chifeng 025450, China; 3. State Key Laboratory of Coal Mine Disaster Dynamics and Control, Chongqing University, Chongqing 400044, China)

Stability analysis of six different types of peach-shaped pillars were carried out using methods of theoretical calculations and the ABAQUS numerical simulation software. First, the stage of mining was divided into four panels during the mining process. Second, the influences of six kinds of parameters of peach pillars on the minimum protective layer thickness under the maximum impact force of the roadway were analyzed based on structural mechanics model. Finally, the residual full length and vertical height of the roadway under the impact of the peach-shaped pillars were screened, and the optimal design scheme was chosen for the peach-shaped pillars. The results show that during the mining process, the stress state of the roof is changed from compressive stress to tensile stress, and the inter-pillar pressure increases, but the top plate and pillar are both stable and do not reach the breaking strength. It is found that the larger the slope is, the thinner the thickness of the protective layer is. With the action of impact loads, the damage degree is smaller for peach-shaped pillar with smaller slope, and the deformation energy is greater for peach-shaped pillar withhigher height. When the slope angle is 60° and the length is 15 m, the design scheme proves to be the best.

peach shaped pillar; impact load; numerical simulation; stability analysis

TD853

A

1672−7207(2019)05−1181−11

10.11817/j.issn.1672−7207.2019.05.022

2018−06−08；

2018−07−28

国家自然科学基金资助项目(51774058, 51504044)；中国博士后科学基金资助项目(2015M570607)；重庆市基础科学与前沿技术研究专项(cstc2018jcyjAX0387, cstc2016jcyjA0558) (Projects(51774058, 51504044) supported by the National Natural Science Foundation of China; Project(2015M570607) supported by the National Science Foundation for Post-doctoral Scientists of China; Projects(cstc2018jcyjAX0387, cstc2016jcyjA0558) supported by the Basic Science and Advanced Technology Research Foundation of Chongqing City)

彭康，博士，副教授，从事岩石力学及采矿方法研究；E-mail：pengkang@cqu.edu.cn

(编辑 伍锦花)