改进人工势场法的移动机器人路径规划

陈金鑫,董 蛟,朱旭芳

(海军工程大学，湖北 武汉 430000)

Khatib在1986年提出了人工势场法,它的基本思想是在机器人周围设计一种类似于电场的势场,机器人的运动依靠势场力进行驱动。障碍物对机器人产生“斥力”,目标对机器人产生“引力”,障碍物斥力和目标引力的矢量和是机器人所受的合力,合力的方向即机器人下一步的运动方向。该方法由于数学原理简单，计算速度快，硬件要求低，被广泛应用于移动机器人路径规划。

同时,传统的人工势场法也存在着缺陷,文献[1]指出该方法依托局部环境信息进行运算,缺少全局信息的指导,存在着陷入局部极小陷阱,产生目标不可达，规划路径徘徊震动等问题。为此,研究人员对此做了大量改进:文献[2]重新定义了势场函数,加入了可调参数,并使用进化算法确定最优参数;文献[3-4]将距离项引入斥力势场函数,解决了局部极小引起的目标不可达问题;文献[5-9]均对势场函数进行了改进,提高了规划路径的质量；文献[10-12]通过增设虚拟目标点的方式引导机器人走出局部极小点;文献[13-14]则从障碍物入手,增设虚拟障碍物,修改障碍物斥力的影响范围,进而达到避碰的目的；文献[15-19]将人工势场法与其他路径规划算法进行融合,取得了不错的避碰效果。以上研究均对人工势场法的发展起到了促进作用,不过部分算法也存在着规划过于复杂、实时性差等问题。

本文为解决人工势场法存在的局部极小问题,提出一种改进模型,根据机器人和障碍物、目标的相对位置偏转斥力的方向,同时自适应调节斥力系数,最后通过Matlab仿真验证了算法的有效性。

1 传统人工势场模型

传统人工势场由两种势场叠加而成,目标点对机器人提供引力,形成引力势场;障碍物则提供斥力,形成斥力势场。障碍物处的势能较高,而目标点处的势能较低,在势场力的驱动下,机器人从势能高的地方向势能低的方向运动,最终找到了一条可以到达目标点的无碰路径。

传统人工势场的引力势场函数为

Uatt(X)=0.5λ1ρ2(X,Xg)

(1)

斥力势场函数为

(2)

式中,X=(x,y)是机器人的位置向量,λ1和λ2分别是引力与斥力增益系数,X、X0、Xg分别代表机器人、障碍物、目标点的空间位置,ρ(X,X0)和ρ(X,Xg)分别代表机器人到障碍物和到目标点的距离,ρ0是障碍物对机器人的影响半径。

对势场函数求解负梯度,即可得到势场力的表达式:

Fatt(X)=-

(3)

Frep(X)=-Urep(X)=

(4)

在上述势场力的作用下,机器人路径规划存在着局部极小问题。一种改进方法是将机器人和目标距离的n次方引入到斥力势场函数中

(5)

相应的,斥力函数修改为:

Frep(X)=-Urep(X)=

(6)

式中,n的取值范围是(0,∞)。修改后的斥力分力Frep1由障碍物指向机器人,分力Frep2由机器人指向目标点,且Frep1随着机器人和目标点距离的减小而减小,如图1所示。

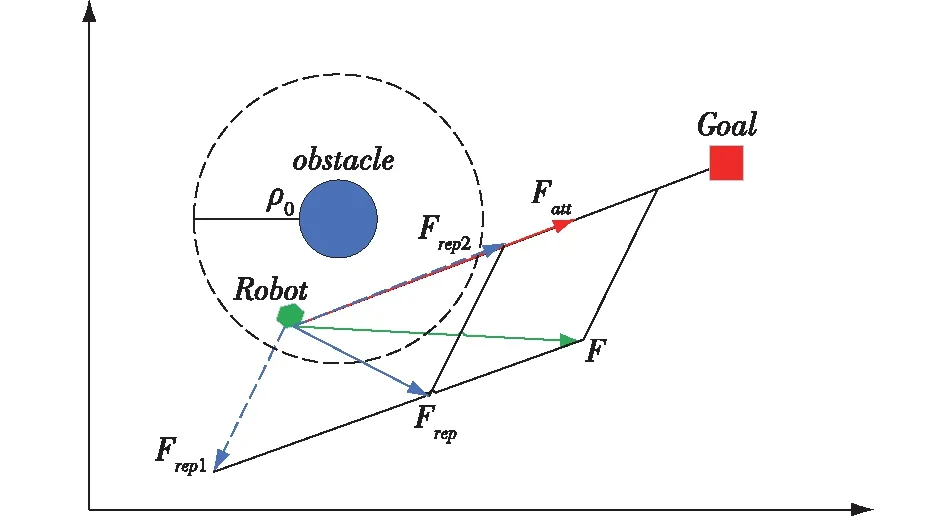
图1 引入距离项后机器人受力示意图

图1所示模型中,斥力随着机器人到目标点距离缩小而减小,同时增加了一个由机器人指向目标点的分力,因此理论上可以解决一类局部极小问题——目标点周围有障碍物而导致目标点不可达的问题。文献[7]对n不同取值对避障效果的影响进行了分析,结果显示确定参数n的过程较为复杂而且不能保证绝对安全的避碰。参数调节不佳时,会出现提前停车或者直接撞向障碍物的情况[12]。第二节针对上述模型的缺陷进行改进,第四节仿真实验中n值取1。

2 基于斥力偏转的改进人工势场模型

基于对极小点问题的几种典型场景的分析,本文总结陷入势场极小点的规律,提出了基于斥力偏转的改进人工势场模型。局部极小点问题可以表现为以下四种典型场景,如图2所示。

a. 机器人、障碍物、目标点共线,障碍物在中间。

b. 机器人、障碍物、目标点共线,目标点在中间。

c. 机器人和目标陷入障碍物包围圈中。

d. 目标在障碍物包围圈中。

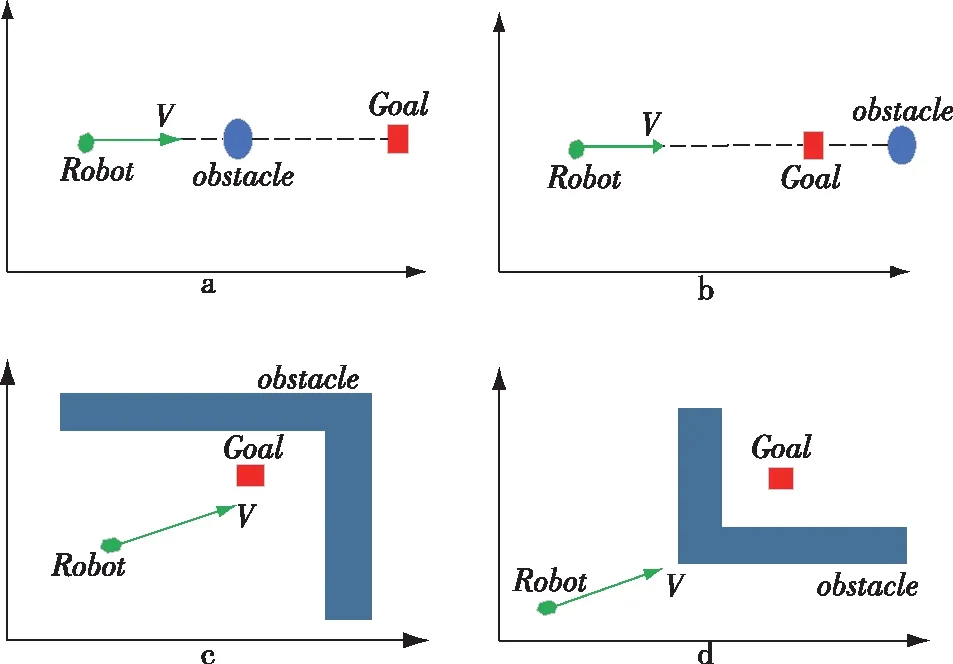
图2 典型局部极小点场景示意图

图2所示场景中,机器人在障碍物前停住,或者沿着障碍物边缘某位置徘徊,实际上是势场对机器人施加的引力和斥力相等,方向相反。此时机器人所处的位置是一个局部势能低点,但不是在目标位置形成的势能低点,这叫做“势场陷阱”。那么只要通过调整,破坏掉引力和斥力这种在数值和方向上的平衡,机器人就能走出“势场陷阱”。基于斥力偏转的改进人工势场模型,针对第一节中的势场模型作了两步改进：修改斥力的指向以及自适应调节斥力系数,破坏局部极小点处势场引力和斥力的平衡。

2.1 改进1——改变斥力分力的方向

势场斥力偏转如图3所示。

图3 势场斥力偏转示意图

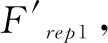
斥力分力Frep1和引力Fatt之间有一个夹角,当夹角为钝角时,机器人存在陷入局部极小点的可能性。进一步分析,当合力F和引力Fatt之间的夹角为钝角时,机器人存在较大可能性陷入局部极小点。通过将Frep1的方向旋转一个角度θ,使得合力F与引力Fatt的夹角小于等于90°,机器人即可避开局部极小点。

旋转角θ的大小和两个要素有关,即角β和距离l。由于角度β不够直观,引入中间变量d来刻画角度θ,表达式为:

d=l·sin(β)

(7)

θ=θ0-μ·d·l

(8)

2.2 改进2——修改斥力增益系数

在保证安全的前提下,当在机器人航向上,障碍物被目标点遮挡,机器人没有必要调整航向;当机器人驶过障碍物时,机器人同样没有必要调整航向。

同时,分析目标点不可达问题,发现机器人之所以难以到达目标点,主要是难以翻越障碍物造成的高势场。如图4,显示的是目的地周围存在四个障碍物的情形下的势场分布。虽然目标点处的势场低,但是障碍物连线附近的势场很高,形成类似势场“高墙”导致机器人难以翻越。如果斥力增益系数能够随着与障碍物的距离增加而递减的话,那么障碍物周围的势场下降的很快,障碍物之间形成的势场“高墙”将不再能拦住障碍物。

图4 目标点周围障碍物及其势场分布示意图

综合以上分析,斥力增益系数λ2的值应当根据一个函数确定,表达式如下:

(9)

式中,λ0是系数基数,m是非负实数,s是机器人与障碍物之间的距离。

3 规划路径评价模型

机器人路径规划问题,首要目标是规划出一条无碰路径。因此机器人根据规划路径巡航的结果有两个,发生碰撞和未发生碰撞,这是一个0-1问题。但是,仅仅根据是否发生碰撞来衡量路径规划的优劣,很难比较各种规划方法的优劣。建立规划路径量化评价模型,模型主要包括四个参数。

参数1:规划路径是否发生碰撞

由于无碰路径是路径规划的首要要求,机器人与障碍物一旦发生碰撞,那么当次路径规划是失败的。

(10)

参数2:规划总时间

实际巡航时,路径总长度的长短,意味着消耗资源的多少。因此,路径总长度越短,那么当次路径规划结果越好。由于人工势场模型未涉及对速度的要求,因此路径长度和巡航时间是成正比的。由于路径是分段规划的,每段规划的路径航向不变,因此巡航总时间可以根据每一段的时间求和得到。

假设路径规划一共分为N段进行,第i个时段的时间长度为Ti,那么规划总时间为

(11)

参数3:最大转弯角速度

假设机器人某次任务规划的起点和终点之间,没有任何障碍物,那么起点和终点之间的直线连线可以作为规划路径,且直线航向时机器人的航向是不变的。实际过程中,由于障碍物的存在,机器人的路径往往不是直线,因此航向也是实时变化的。航向角对时间的变化率,即机器人转弯的角速度。转弯角速度反映了,规划的路径对机器人机动性能提出的要求。由于路径规划分段进行,因此使用相邻规划时段的航向差分,作为航向角速度。

设第i个时段的航向为Ci,第(i+1)个时段的航向为Ci+1,那么航向差分为

式中,stepi是第i个规划时段的时长。

在整个规划时间内,取航向差分的绝对值的最大值作为最大转弯角速度,即

ωmax=max{ΔC1,ΔC2,…,ΔCi,…, ΔCn-1},
(i=1,2,…,N-1)

(12)

参数4:保持直线航行时间

从参数1和参数2的确定过程来看,在路径总长度相同的情况下,直线航行时间越长,意味着规划路径对机器人机动性要求越低。由于航向实时变化,航向保持不变的概率较低,因此设定航向变化阈值R。

若存在ΔCi≤R,那么第i个时段视为“保持直线航行”;若ΔCi>R,那么第i个时段视为 “未保持直线航行”。设定属性变量flagkeep,取值如下

统计“保持直线航行”的时段数目,得到机器人保持直线航行的时间

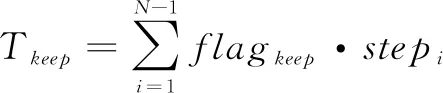
(13)

根据公式(10)-(13),给出规划路径的评价值

(14)

式中,r1、r2、r3为三个正系数,且满足r1+r2+r3=1。评价值value越大,表明规划路径的质量越高。

4 仿真校验及分析

使用Matlab软件编写避碰仿真系统,对基于斥力偏转的模型进行仿真验证,并利用路径评价模型对规划的路径进行评价,和传统人工势场模型、加入距离项后的势场模型的避碰效果进行对比。

根据前文给出的四种障碍物环境进行仿真,结果如图5所示。

图5 典型局部极小点环境下避障规划仿真图

分析图5得到,应用基于斥力偏转的改进人工势场模型后,机器人能够避开路径上的障碍物,并且在目的地被障碍物包围的时候,仍然可以寻找路径到达目的地。

本文以“机器人与障碍物会遇”这一情形为例,分别针对传统人工势场模型、加入距离项后的势场模型、基于斥力偏转的改进人工势场模型,使用仿真系统进行仿真,结果如图6所示。应用规划路径评价模型对各条规划出的路径进行评价,结果见表1。

表1 相同环境下三种模型的规划效果评价数据表

图6 相同环境下三种模型的规划效果对比图

根据图6分析,三种人工势场模型规划的路径均是无碰的,说明人工势场法应用于机器人巡航任务是比较安全的。图6中三幅子图对比可以得到,传统人工势场法的总路径较长,而且机器人巡航在做转弯动作时基本是急转弯;修改斥力势场函数的模型规划出的路径,转弯动作稍缓;而基于斥力偏转的模型规划出的路径是相对比较平滑的。

在表1中,参数flagcollision显示,规划出的三条路径均是无碰的,和图中实际情况符合。对比参数Ttotal,发现传统人工势场模型的规划时间最长,基于斥力偏转的改进模型规划时间最短,说明模型的改进缩短了机器人的巡航路径的长度。对比参数ωmax发现,对应传统模型和修改斥力势场函数的改进模型的数值较大,模型对机器人的转向能力提出了很高的要求。而基于斥力偏转的改进模型,ωmax值大幅减小,说明模型规划的路径非常平缓,对机器人的转向能力要求较低。对比参数Tkeep,发现对应基于斥力偏转的改进模型的值最大,说明规划路径中更大部分是直线巡航,进一步降低了对机器人自身机动性能的要求。最终路径评价值value显示,基于斥力偏转的改进模型规划路径的评价值,明显高于其他两种模型的规划路径的评价值,说明基于斥力偏转的改进模型提高了巡航路径的质量。

5 结束语

本文提出的基于斥力偏转的改进人工势场模型,主要完善了传统人工势场法的几个缺陷:第一,机器人巡航过程中,出现与障碍物、目的地共线的情况时,易陷入局部势场最低点而提前停车。基于斥力偏转的改进模型,通过提前转弯解决了这个问题,同时解决了传统模型中出现的规划航向变化过大导致机器人不能及时反应的问题。第二,机器人巡航过程中,目的地周围有障碍物群形成的高势场,导致机器人无法靠近目的地。即使是修改斥力势场函数的改进模型,在斥力增益系数不变的情况下,也易陷入局部势场最低点,或者直接撞上障碍物。基于斥力偏转的改进模型,自适应调整斥力增益系数,降低了障碍物连线之间的势场“门槛”,使得机器人可以顺利到达目的地。