探索组合图形教学下的数学思维

陈玉娴

摘 要 小学生的数学思维发展一般是从具体操作形成的具体思维开始再逐步转化为抽象思维。数学是一门很有逻辑性且有很强的数学思维贯穿其中。本篇论文以组合图形的面积教学为主要探讨方向，力求让学生在观察、操作、合作、比较中学会计算组合图形面积的多种方法并进行优化选择。学生通过一系列解决数学问题的过程中，收获学习方法，并在反思与悟错中提升数学解决问题的能力。

关键词 组合图形 小学数学 数学思维 面积计算

中图分类号：G623.5文献标识码：A

《组合图形的面积》这节课是在学生已经掌握了长方形、正方形、平行四边形、三角形和梯形面积的计算。在此基础上，再加上学生可以对单一图形进行简单分析具备一定的思维能力。因此这节课教师可以温故知新，通过建立空间观念、发展数学思维，运用综合能力解决数学问题。

1分析教材，明确教学目标

数学思维渗透在每节数学课中，而组合图形这节课中的数学思维比较突出和具代表性，因此在授课前，笔者进行细致全面的教材分析，例如从P99中学生要：（1）学会从新图形中发现旧知（以前学过的图形）新知与旧知的迁移，（2）通过旧知分别计算图形面积，再加起来获得新图形面积（启发学生用多种方法求组合图形面积）;P100 1利用小方格估算图形面积（考察学生空间想象能力）;P101习题1复习旧知求图形面积2～6考察学生把生活实际中的图形抽象成已经学过的图形，并考察不同的面积算法7考察面积估算。8、9利用小方格考察面积估算。10 复习巩固以上学过的求组合图形面积并创新让学生设计一种方案求组合图形面积（开放题）。

2组合图形中渗透的数学思维

本节课属于图形与几何的知识，力图让学生认识并欣赏自然界和现实生活中的軸对称图形、中心对称图形以及平移在自然界和现实生活中的应用。因此教学过程中笔者将结合图形与几何知识的要点本课分为三个部分：复习导入，引入新知;创设情境，自主探索;拓展练习，应用提高。

课堂之初笔者首先引导学生回顾学习过的简单图形及其面积计算方法（长方形、正方形、三角形、平行四边形和梯形）;通过借助课件的动态特点引导学生理解什么是组合图形、引出组合图形的具体概念。

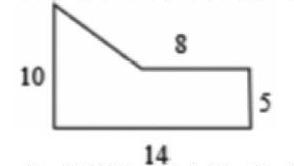
接着通过创设求草坪面积的情境（如图），提出问题（复杂的组合图形的面积没有学过，怎么办？），让学生自己思考，结合教师适当引导，引出“转化”思想，即将组合图形转化为学过基本图形来求面积。

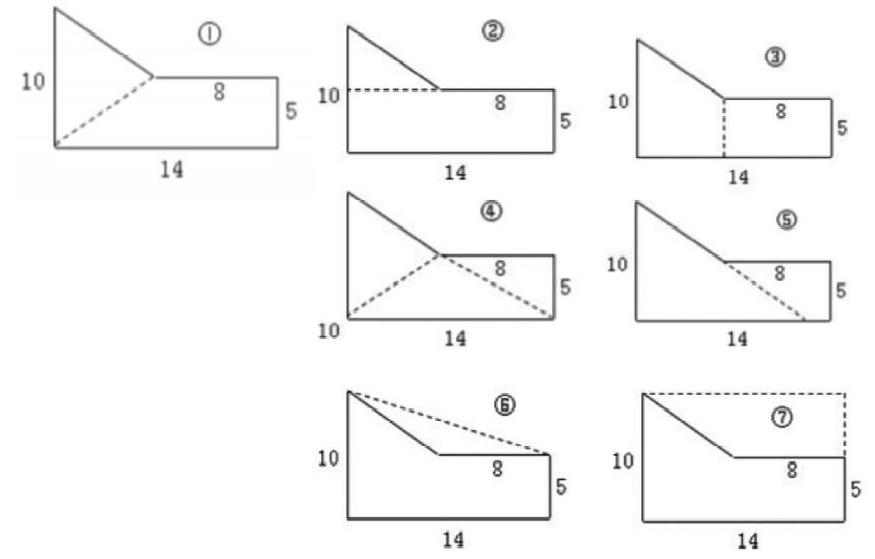
学生通过小组合作学习，在纸上采用多种方法对组合图形进行割补，教师巡视指导。学生分割结束后，全班进行交流分享不同的割补方法。教师并将其展示在黑板上（可能有以下七种）。

此刻笔者引导学生观察所有的割补情况，提出问题（这些割补的方法，其不同点和相同点分别是什么？），并进行全班交流。学生在求面积的时候会发现第5种割补方法无法求出图形的面积，发现问题（为什么有些割补方法无法计算出组合图形的面积？）并进行全班交流，引导学生认识到：将组合图形转化为基本图形不仅割补方法要简单，还要有足够的数据支持，能算出面积。即割补不仅要分得简单，还要可行。进而总结计算组合图形的面积的方法步骤，学生在这一步骤中当学生看到这个图形时，他们会发现运用原来的基本图形面积的计算公式，无法直接求得它的面积。那该怎么办呢？可以让学生集中注意力，促使他们主动思考。这个过程，其实也就是学生区别组合图形和基本图形、认识组合图形的学习过程。

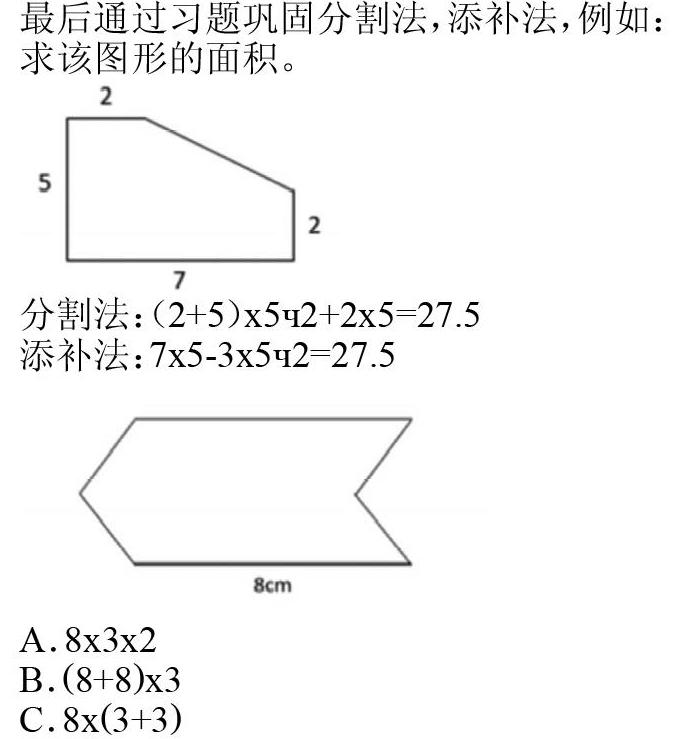
最后通过习题巩固分割法，添补法，例如：

求该图形的面积。

分割法：（2+5）x5？+2x5=27.5

添补法：7x5-3x5？=27.5

A.8x3x2

B.（8+8）x3

C.8x（3+3）

本节课笔者主要通过旧知引新知，运用学过的图形将其组合在一起，通过动画的形式直观形象的展示，让学生了解组合图形的特点，进而运用各个图形的计算特点求组合图形的面积，整节课不仅可提升学生综合运用的能力，同时学生可以在解决数学问题时学会数学转化的思想，通过运用多种方法解决问题只培养优化意识，从而训练学生的思维敏捷性和解决问题的能力。

3结束语

在图形与几何课堂课程中，教师应了解本班学生抽象思维发展情况，结合本班学情借助多媒体以直观形象的几何图形特点展现出来，有助于转化抽象的数学问题，便于学生理解和促进其抽象思维发展，从而发展几何直观和空间观念，锻炼其逻辑思维能力和解决问题能力。在自主探索面积的环节中渗透转化思想和优化思想，进而扩展空间观念，培养学生的创造性思维。

参考文献

[1] 于海娜.小学数学课堂教学中创造性思维的培养——《组合图形面积》教学案例[J].新课程（上）， 2017（07）：162.

[2] 陈贤深，谢清霖.动手“做”数学 思维求创新——人教版五年级上册《组合图形面积的计算》设计片段及评析[J].福建教育，2006（7A）：44-45.