An Algorithm for Mining Gradual Moving Object Clusters Pattern From Trajectory Streams
2019-06-12YujieZhangGenlinJiBinZhaoandBoSheng
Yujie Zhang,Genlin Ji, ,Bin Zhao and Bo Sheng
Abstract:The discovery of gradual moving object clusters pattern from trajectory streams allows characterizing movement behavior in real time environment,which leverages new applications and services.Since the trajectory streams is rapidly evolving,continuously created and cannot be stored indefinitely in memory,the existing approaches designed on static trajectory datasets are not suitable for discovering gradual moving object clusters pattern from trajectory streams.This paper proposes a novel algorithm of gradual moving object clusters pattern discovery from trajectory streams using sliding window models.By processing the trajectory data in current window,the mining algorithm can capture the trend and evolution of moving object clusters pattern.Firstly,the density peaks clustering algorithm is exploited to identify clusters of different snapshots.The stable relationship between relatively few moving objects is used to improve the clustering efficiency.Then,by intersecting clusters from different snapshots,the gradual moving object clusters pattern is updated.The relationship of clusters between adjacent snapshots and the gradual property are utilized to accelerate updating process.Finally,experiment results on two real datasets demonstrate that our algorithm is effective and efficient.
Keywords:Trajectory streams,pattern mining,moving object clusters pattern,discovery of moving clusters pattern.
1 Introduction
The increasing pervasiveness of object tracking leads to huge volumes of spatio-temporal data collected in the form of trajectory streams.Discovering gradual moving object clusters pattern [Hai,Ienco,Poncelet et al.(2012)] (i.e.,GC-Pattern)from these streams is an important mining problem.GC-Pattern is a list of clusters and adjacent clusters need to satisfy time threshold,object containment relationship and clusters size threshold requirements.GC-Pattern was proposed to capture the gradual object moving trend.
The discovery of GC-Pattern from trajectory streams is critical for real time applications.For example:traffic jam discovery in transportation management,event detection in public security and invasion monitor in military surveillance [Zhou,Liang,Li et al.(2018)].Despite of the wide applications,the discovery of GC-Pattern from trajectory streams is not efficiently supported in existing systems,partly due to the following challenges:
Instantaneity:Trajectory streams arrives rapidly in a short period of time and its size keeps growing as time goes.Therefore,the algorithm for discovering GC-Pattern from trajectory streams needs to be designed with low computation cost and memory limitation.
Parameter insensitivity:The distribution of trajectory streams is unknown and constantly change.Hence it is difficult to set an appropriate threshold value of parameters when clustering moving objects.So the mining algorithm should be insensitive to the parameter setting.
Pattern updating:The GC-Patterns at previous time window include a lot of valuable information.This information usually can be utilized to reduce the repeated computation,save the cost of the computation,and boost the efficiency of the mining algorithm.Hence,when trajectory streams arrive,there is no need to process past data.By taking full use of the GC-Patterns discovered earlier,the mining algorithm of GC-Pattern should be effective to update patterns.
However,since the existing mining algorithms of GC-Pattern are designed for static trajectory datasets,it cannot effectively deal with the problems mentioned above.In this paper,we propose a GC-Pattern mining algorithm,which contains three phases:(1)Clustering moving objects,(2)obtaining all related-clusters in current time window,(3)updating GC-Pattern.
The main contributions of the paper are as follows:
(1)GC-Pattern mining algorithm DStream-GC is proposed to discover GC-Pattern from large scale trajectory streams.
(2)Density Peaks (DP)Clustering [Rodriguez and Laio(2014)] is introduced to clustering moving objects since the algorithm is not sensitive to the parameter.Moreover,a data structure named moving micro-group is used to speed up the clustering tasks.
(3)GC-Pattern updating algorithm Update-GC is proposed.The related-clusters and two pruning rules are developed to accelerate the updating process.
The remaining of the paper is organized as follows.Section 2 introduces the related works.The definition of GC-Pattern is given in Section 3.The algorithm for discovering GC-Pattern is presented in Section 4.Experiments testing effectiveness and efficiency are shown in Section 5.Finally,our research is concluded in Section 6.
2 Related works
GC-Pattern [Hai,Ienco,Poncelet et al.(2012)] is a special type of moving clusters pattern that models the behavior of the moving objects travelling together.There are a bunch of works on mining moving clusters pattern from moving object trajectories.These works can be categorized into two aspects of research:
Moving clusters pattern discovery from static trajectory data.One of the earliest works is Flock [Benkert,Gudmundsson,Hübner et al.(2010)] discovery.Flock is defined as a group of moving objects moving in a disc of a fixed size for k consecutive timestamps.Another similar definition,Moving Cluster [Kalnis,Mamoulis and Bakiras (2005)],tries to find a group of moving objects which have considerably portion of overlap at any two consecutive timestamps.A recent research by Jeung et al.[Jeung,Shen and Zhou (2008);Jeung,Yiu,Zhou et al.(2010)] proposes Convoy,an extension of flock,where spatial clustering is based on density.Comparing with all these definitions,Swarm [Li,Ding,Han et al.(2010)] is a more general one that does not require k consecutive timestamps.More recently,Gathering [Zheng,Zheng,Yuan et al.(2013)] was proposed to capturing groups where a part of objects were allowed to change.However,all the above methods cannot capture the moving trends of objects which can be very useful for better understanding the natural moving behavior in various real world applications.
Moving clusters pattern discovery from trajectory streams.Vieira et al.[Vieira,Bakalov and Tsotras (2009)] propose an algorithm to discover the existing pattern Flock from trajectory streams.Flock requires moving objects to continuously move in a circular area of a given radius.In order to reduce computation load,the index technique is introduced.Tang et al.[Tang,Zheng,Yuan et al.(2012);Tang,Zheng,Yuan et al.(2014)] propose the discovering algorithm of Traveling Companion.Traveling Companion requires moving objects to be connected in density on consecutive timestamps.In order to improve the efficiency of clustering algorithm,a special data structure named traveling buddy is proposed to store and maintain the relationship between moving objects.Li et al.[Li,Ceikute,Jensen et al.(2013)] propose Group pattern,that is,the moving objects are connected in density for a period of time.Since the Group pattern limits time strictly,information such as the direction and speed of the moving objects is used to judge whether it is necessary to update the pattern when the trajectory streams arrives.In addition,Zheng et al.[Zheng,Zheng,Yuan et al.(2014)] use the existing traveling buddy structure to implement the algorithm of Gathering [Zheng,Zheng,Yuan et al.(2013)] discovery.Lan et al.[Lan,Yu,Cao et al.(2017)] further propose an online Evolving Groups discovery algorithm.Both Gathering and Evolving Groups pattern require the moving objects stay stable,and thus they adopt an approximate approach to reduce invalid operations.However,since GC-Pattern requires adjacent clusters to satisfy time threshold and object containment relationship,the above methods are not applicable to discover GC-Pattern from trajectory streams.
3 Problem statement
Let O={o1,…,on} be a set of moving objects where each object oireports its positions in fixed interval of time.We assume that the position of each object is reported at the same timestamp and term the positions of all objects at a single timestamp as a snapshot.Thus,we consider trajectory streams S as a sequence of snapshots {s1,…,si,…}.A database of clusters C={C1,…,Ci,…} is a collection of the moving object clusters at snapshots{s1,…,si,…}.The cluster Ciis defined as the clustering results of densitybased clustering at snapshot si.Given a cluster c ∈Ci,|c| and t(c)are respectively used to denote the number of objects belonging to cluster c and the timestamp that c involved in.
Let st-w+1,st-w+2,…,stbe the set of snapshots in current window [t-w+1,t] where w is the length of the time window.The window slides by one snapshot that removes the snapshot of time instance t-w+1 and includes the snapshot of time instance t+1 in current window.Tab.1 lists the notations used throughout this paper.

Table 1:List of Notations
Definition 1 (GC-Pattern).Given a list of clusters C∗={c1,…,cn},a minimum threshold mint,a time window size w.C∗is a GC-Pattern if:
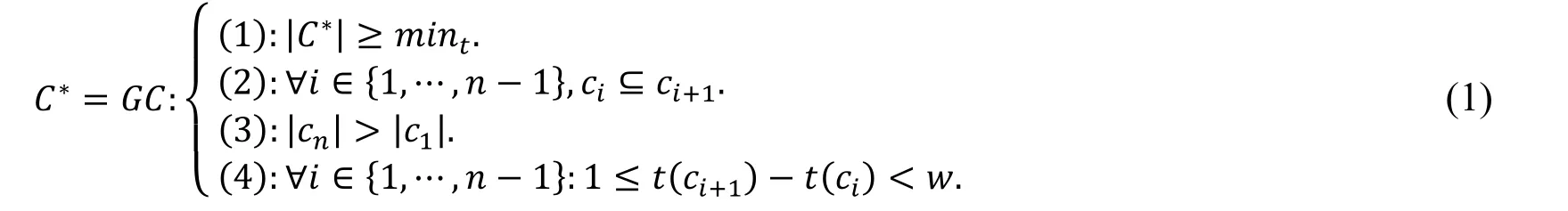
Let s1,s2,…,stbe the series of snapshots that have arrived so far.If C∗={c1,…,cn} is a GC-Pattern and the last element of C∗belongs to the newly arrived snapshot,i.e.,t(cn)=t,then C∗is a GC-Pattern in current time window.
Fig.1 illustrates an example of GC-Pattern.There are 6 objects,S={s1,…,s6},C={{c1},{c2},{c4},{c6}}.Let mint=3,w=3,C1={c1,c2,c4} and C2={c1,c2,c4,c6} are GC-Patterns.C2={c1,c2,c4,c6} is also a GC-Pattern in current time window.

Figure 1:An example of GC-Pattern
Problem Definition:Let s1,s2,…,stbe the series of snapshots that have arrived so far.The problem is to discover all the GC-Patterns in current time window[t-w+1,t].
4 Discovery of GC-Pattern
4.1 The algorithm for mining GC-Pattern from trajectory streams using sliding window models
This paper proposes algorithm DStream-GC to discover GC-Pattern from trajectory streams.First,the definition of the GC-Pattern candidate is given.
Definition 2 (GC-Pattern Candidate).Given a list of clusters C∗={c1,…,cn},a minimum threshold mint,a time window size w.C∗is a GC-Pattern candidate if:
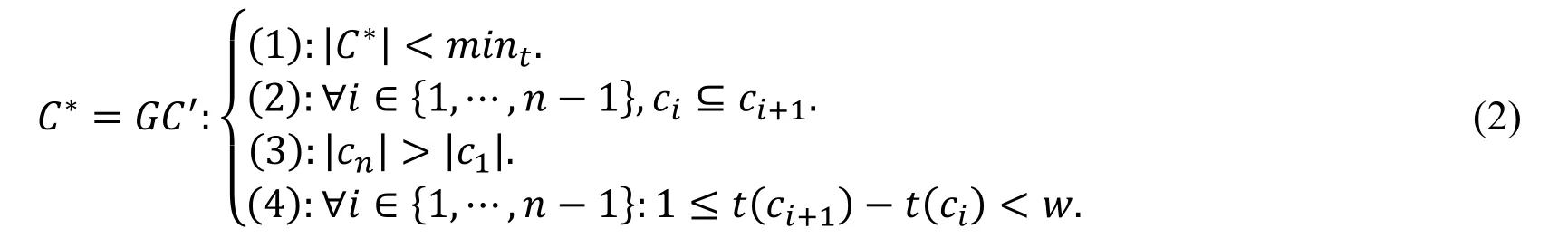
If C∗={c1,…,cn} is a GC-Pattern candidate and the last element of C∗belongs to the snapshots in current time window[t-w+1,t],i.e.,t(cn)>t-w+1,then C∗is a GC-Pattern candidate in current time window.Intuitively,the GC-Pattern candidate does not require duration greater than time threshold.In the trajectory streams,data continues to arrive.For the GC-Pattern with shorter duration,its lasting time is likely to increase continuously,and meets the time requirement as time goes by.Therefore,when trajectory streams arrive,the previous GC-Pattern candidates are updated.Once the duration meets the requirement,it will be reported as a GC-Pattern in current time window.
Algorithm DStream-GC includes the following three stages.
(1)clustering moving objects
The clustering method based on the density peaks is used to cluster the moving objects at current snapshot si.The clustering results are a set of clusters Ci.
(2)obtaining related-clusters in current time window
The related-clusters in current time window of every cluster in Ciare obtained by using the relationship between clusters at adjacent snapshots.
(3)updating GC-Pattern
The updating operation of GC-Pattern is implemented by intersecting every cluster in Ciwith GC-Patterns and GC-Pattern candidates in previous time window.The relatedclusters are used to speed up the updating process.Finally,all the updated GC-Patterns satisfying the conditions are returned.
The process of GC-Pattern discovery from trajectory streams is shown as algorithm DStream-GC.When the snapshot siarrives,the moving objects are gathered into clusters (line 3).Then the related-clusters in current time window of every clusters of siis obtained (line 4).By intersecting each cluster of siwith GC-Patterns and GC-Pattern candidates in previous time window,the pattern updating operation is conducted (line 5).After that,GC-Pattern candidates in current time window is updated (line 6).Finally,GC-Patterns that meet the time requirement are returned (lines 7-10).
Algorithm DStream-GC
Input:S,GCc′,GC′,mint,γ,dc,w
Output:GC

For the three stages of algorithm DStream-GC,this paper proposes corresponding algorithms to improve the discovering efficiency.The algorithm designed for each stage is described below.
4.1.1 Clustering moving objects
The algorithm for discovering GC-Pattern from static trajectory data needs to carry out density-based clustering (DBSCAN)at every snapshot.The time complexity of this operation is O(n2),where n is the number of moving objects.Subsequently,if the number is large,the method cannot meet the timeliness requirement of trajectory streams processing.
Tang et al.[Tang,Zheng,Yuan et al.(2012)] proposed a traveling buddy data structure to store and maintain the relationship between moving objects.By utilizing traveling buddy structure,the algorithm saves the cost of the computation effectively and improves the clustering efficiency.However,when updating the center point of the traveling buddy,the accumulation of the offset increases the sensitivity of outliers of the algorithm.Gong et al.[Gong,Zhang and Yu (2017)] used a cluster-cell data structure in data stream clustering to represent a set of close points.However their methods cannot apply to discover the movement pattern directly due to the time series property of spatio-temporal data.In this paper,the moving micro-group concept is proposed to represent the small group of moving objects with stable structure.When the trajectory streams arrive,the algorithm accelerates the clustering process by maintaining the information of moving micro-group and avoiding re-clustering moving objects.
Definition 3 (Moving Micro-Group):A moving micro-group g represents a group of moving objects staying closer,which can be described by a three-tuple {rg,ρg,δg}:
(1)rgis the representative object of a moving micro-group g.The moving micro-group g represented by rgsummarizes a set of objects Pgsatisfying:(a)where pi∈Pgand R is the set of the representative object;(b)for ∀pi∈Pg,|pi,rg|≤γ,where γ is the radius threshold.
(2)ρgis the density of a moving micro-group g,which is defined as the number of moving objects contained in the moving micro-group g,i.e.,ρg=|Pg|.
(3)δgis the dependent distance from rgto its nearest moving micro-group representative object with higher density,i.e.,
During the initialization phase of moving micro-groups,each moving object is assigned to a moving micro-group that meets two conditions in (1).The initialization step only needs to be carried out once and the moving micro-groups are dynamically maintained along the stream.
There are two kinds of operations to maintain moving micro-groups on the trajectory streams:updating representative objects and updating the other moving objects.The updating process of the moving micro-groups is shown as algorithm Update-MMG.When the trajectory streams arrive,the representative objects at the last snapshot are updated (lines 1-5),and then the remaining moving objects are assigned to the corresponding moving micro-group using definition 3 (lines 6-8).After that,the algorithm assigns the new arriving objects at current snapshot to the corresponding moving micro-group (line 9).Finally the updated moving micro-groups are returned (line 10).
Algorithm Update-MMG
Input:si,G′,γ
Output:G

An example of updating moving micro-groups is shown in Fig.2.There are three moving micro-groups at snapshot s1.The representative objects of g1,g2,g3are 1,5,and 8 respectively.When the snapshot s2arrives,the moving micro-groups at snapshot s1are updated.Moving micro-groups g1,g2have changed,with object 4 in g1moving to g2.The updated moving micro-groups are g1′,g2′,g3′.
When the snapshot arrives,the algorithm updates the moving micro-groups at previous snapshot,and then conducts the clustering operation with the updated moving microgroup as a basic unit.Algorithm DBSCAN is employed in existing methods based on static trajectory datasets to obtain the clusters on current snapshot.However,DBSCAN is not well used to clustering moving objects on trajectory streams due to the property of sensitivity to parameters.

Figure 2:An example of updating Moving Micro-Groups
In 2014,Rodriguez et al.proposed a density-based clustering algorithm (DP)[Rodriguez and Laio (2014)].Since the algorithm only needs one parameter and is insensitive to this parameter,it has been widely used in the industry and academia [Sun,Geng and Ji (2015);Chen,Lai,Qi et al.(2016)].In this paper,algorithm DP is exploited to complete the clustering operation of moving objects.
Letmbe the average number of moving micro-groups and n be the number of moving objects.The time complexity of the moving micro-groups updating algorithm is O(m2+mn),and the time complexity of the DP algorithm based on moving micro-groups is O(m2).Even in the worst case,if the objects are sparse and each of them is a moving micro-group,where m=n.The time cost of the clustering process is still O(n2).In fact,the value of m is much smaller than n,so the clustering algorithm proposed in this paper is effective.
4.1.2 Obtaining related-clusters in current time window
After completing the clustering operation,the discovering algorithm needs to update the pattern.The basic method is to intersect each cluster at current snapshot with each GCPattern and GC-Pattern candidate in previous time window respectively.Let the average number of objects in cluster be n,the size of the time window be w,and the average number of GC-Pattern candidates at each snapshot in the time window is m.The time complexity of intersection operation is O(wmn).
In this paper,we develop new techniques to improve the efficiency of intersection operation.By utilizing the connections between clusters at adjacent snapshots,the concept of related-cluster is proposed.The related-clusters are helpful for reducing the number of the intersection.The concept of related-cluster is given below.
Definition 4 (Related-Cluster):Let current time window be [t-w+1,t].Given a cluster c at snapshot st,if the cluster c′at snapshot sj(t-w+1 ≤j<t)contains at least one object of cluster c,then cluster c′is related with cluster c,that is,cluster c′is a related-cluster in current time window of cluster c.
As shown in Fig.3,there are four snapshots s1,s2,s3,s4.The ellipses in the figure represent the clusters generated by clustering operation.Assuming w=3,the related-clusters in current time window at snapshots s1,s2,s3,s4is listed at the bottom respectively.Where ci.rcsjrepresents the set of related-clusters of cluster ciat snapshot sj.

Figure 3:An example of obtaining Related-Clusters
Before updating patterns,the related-clusters in current time window of the clusters at current snapshot are obtained by a small amount of calculations.The process of obtaining related-clusters is shown as algorithm Obtain-RC.First,the algorithm obtains the related- clusters ci.rcsj-1of cluster ciat snapshot sj,with moving micro-groups as basic units.If the elements of the moving micro-group are unchanged,the algorithm only need to add the cluster which the moving micro-group belonged to snapshot sj-1to ci.rcsj-1(lines 1-3).Otherwise,the clusters which the changed elements belong to snapshot sj-1are also added to ci.rcsj-1(lines 4-9).After obtaining ci.rcsj-1,the algorithm obtains the relatedclusters in current time window ci.rcsWwith excepts of related-clusters at snapshot sj-1(lines 10-14).Finally,the related-cluster set RC in current time window of all clusters at snapshot sjis returned (lines 16).
Algorithm Obtain-RC
Input:G,C,w
Output:RC

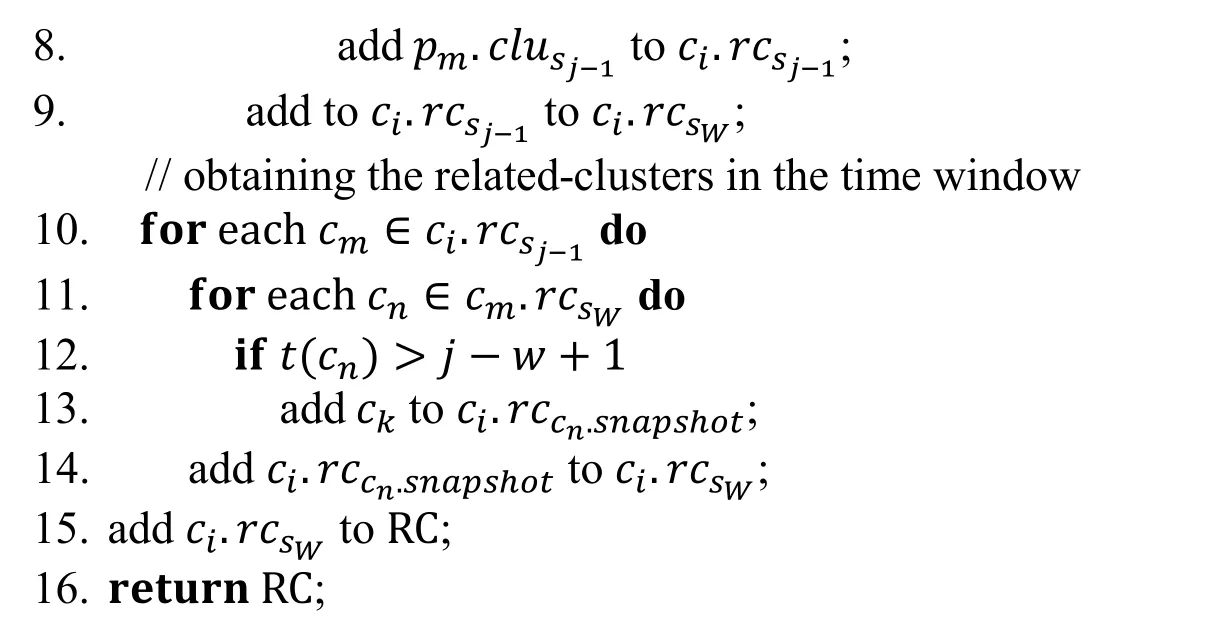
4.1.3 Updating GC-Pattern
Since the discovering algorithm updates the patterns by conducting intersection operation,improving the intersection efficiency becomes the most important factors of updating process.In Fig.3,considering the basic intersection method,c9need to intersect with every element of the clusters set {c5,c6,c7,c8} at snapshot s2and {c1,c2,c3,c4} at snapshot s1respectively.However,it is obvious that only the intersection operations of c5,c6with c9can produce valid results since c5and c6has the same elements with c9.It is the same as the snapshot s1,only the intersection operations of c1,c2with c9are effective.In other words,for the intersection operation of the cluster,it is only necessary to intersect the cluster with its related-clusters.For those unrelated-clusters,even if the intersection is performed,no effective results can be produced.Based on the above analysis,this paper uses the related-clusters to reduce intersection computation and accelerate the pattern updating process.
In addition,in order to further improve the intersection efficiency,this paper proposes two pruning rules,length pruning rules and backward pruning rules to optimize the pattern updating process.Given a cluster ciand its related-cluster cj,if|ci|<|cj|,then cjis pruned by length pruning rules.Given a GC-Pattern Candidate C={c1,c2,…,cj},if there is a cluster c′(t(c′)>t(cj)) at the current snapshot and C∗=C ∪c′satisfies the gradual property,then the intersection operation of ck(ck∈C &k<j)and c′can not generate qualified candidate(without cj),so ckis pruned by backward pruning rules.
The process of pattern updating based on the related-clusters and two pruning rules is shown as algorithm Update-GC.First,all the related-clusters in current time window of each cluster ciat current snapshot are obtained (lines 1-2).For each related-cluster ck,it is judged whether it can pass the length-based pruning rule (lines 3-4).If ckis not pruned,the algorithm continues to judge whether it can pass the backward pruning rule.If it is also not pruned,the algorithm will intersect ciwith ck(lines 5-6).If the length of the intersection result is greater than or equal to the length of the related-cluster ck,the algorithm obtains the set of GC-Patterns and GC-Pattern candidates P whose last cluster is ck(lines 7-8).For each GC-Pattern and GC-Pattern candidates of P,it will be updated by intersecting with ci.Then the updated GC-Pattern and GC-Pattern candidates are added to the set of GC-Pattern GC∗in current time window (lines 9-10).Finally GC∗is returned (line 11).
AlgorithmUpdate-GC
Input:C,RC,GCc′,GC′,w
Output:GC∗


Figure 4: An example of GC-Pattern discovery
Fig.4 describes the process of discovering GC-Patterns.When the trajectory streams arrive,the clustering operation is performed and the moving objects are gathered into clusters.After that,the related-clusters in current time window of clusters at current snapshot are obtained.By using the length pruning rule and the backward pruning rule,those unqualified related-clusters are pruned.In the figure,the clusters in the solid line frame and the dotted line frame are related-clusters pruned by the length pruning rule and the backward pruning rule respectively.By intersecting related-clusters passing two pruning rules with GC-Patterns and GC-Patterns candidates in previous time window,the discovering algorithm completes the pattern updating tasks.Finally,those qualified GCPatterns which bold in the figure is reported.
5 Experiments
5.1 Experimental setting
In this section,the proposed algorithm is evaluated using two real trajectory data sets.The swainsoni dataset [Hai,Ienco,Poncelet et al.(2012)] contains 43 trajectories of swainsoni and 764 timestamps.The start timestamp of the dataset is August 18,1995,and the end timestamp of the dataset is June 24,1998.The taxi dataset contains 13000 trajectories of taxi and 1400 timestamps.It is the GPS data of taxi in Shanghai at April 1,2015.
Since the discovering algorithm of GC-Pattern from trajectory streams has not been reported,the proposed algorithm DStream-GC is compared with ClusterGrowth,which is used to discover GC-Pattern from static trajectory data.DBSCAN algorithm is adopted to realize clustering procedures of ClusterGrowth.Linear interpolation is used to fill in the missing data.The experimental parameter settings are shown in Tab.2,where r is the radius threshold of the moving micro-group,cutoff distance dcis the parameter of DP algorithm,mint is the time threshold of the GC-Pattern.The parameters of DBSCAN are pts and eps.The experiments are conducted on a PC with Intel 4590 CPU(3.30HZ)and 4GB memory.All the algorithms are implemented in Java.
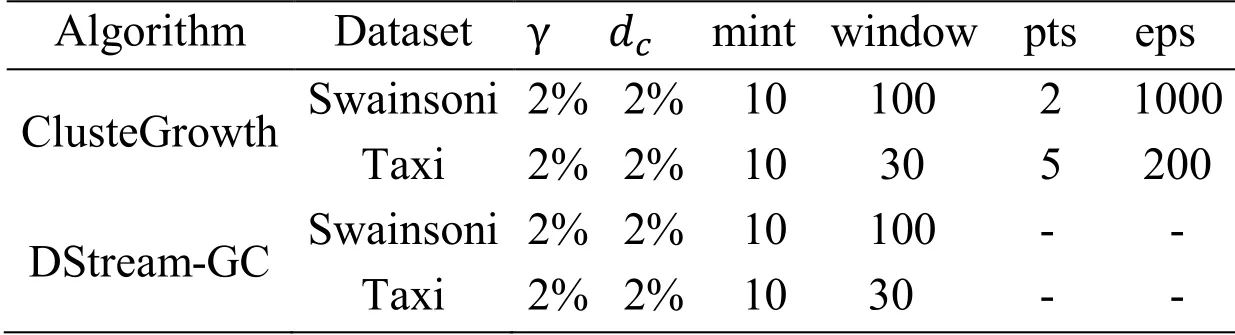
Table 2:Experiment parameters of ClusterGrowth and DStream-GC
5.2 Effectiveness analysis of algorithm DStream-GC
To demonstrate the effectiveness of algorithm DStream-GC,swainsoni dataset is used during experiments.In the comparison,the algorithm ClusterGrowth is employed.
Tab.3 demonstrates a GC-Pattern discovered by DStream-GC on swainsoni dataset.The first row in the table shows the date of moving objects stay together.The second row and third row illustrate the number of objects traveling together and their location respectively.It is observed that two objects set out from Colorado,with the scale increasing continuously to 4,5,8,10,until the number reaching 11 when they arrive in Colombia through the ocean.It is the same with the result of algorithm ClusterGrowth.

Table 3:An example of GC-Pattern on swainsoni dataset
5.3 Efficiency analysis of algorithm DStream-GC
In this subsection,we conduct experiments on taxi dataset to evaluate the efficiency of the algorithms for discovering GC-Pattern.
5.3.1 Efficiency analysis of algorithm DPCluster-MMG
In the first part of experiments,we analyze the efficiency of DP clustering based on moving micro-groups.In the beginning,we test DPCluster-MMG with different radius threshold γ from 0.5% to 3%,and record the number of moving micro-groups and the running time of DPCluster-MMG.One can clearly learn from Fig.5(a)that the number of moving micro-groups whose members are changed is at most 25% of the total number of moving micro-groups,and most of the moving micro-groups remain unchanged.Furthermore,as the radius threshold γ increases,the number of moving micro-groups continues to decrease and the number of moving micro-groups stay unchanged shows an exponentially decline distribution.This is consistent with the theory that the larger scale of the moving microgroup,the greater probability of change.In addition,in Fig.5(b),DP clustering based on moving micro-groups (DPCluster-MMG)is compared with DP clustering based on moving objects (DPCluster-MO).It is found that the running time of the DPCluster-MMG algorithm proposed in this paper is much smaller than DPCluster-MO.Further observations show that DPCluster-MMG has the lowest time overhead when γ is 2%.On the one hand,when the value of γ is small,the size of the moving microgroup is small,which can't give full play to advantages of small group.When γ is large,since there are many members in the moving micro-group,the possibility of change is larger,which involves high updating overhead.Based on the above analysis,the value of γ is uniformly selected as 2% in the experiments of efficiency and effectiveness.
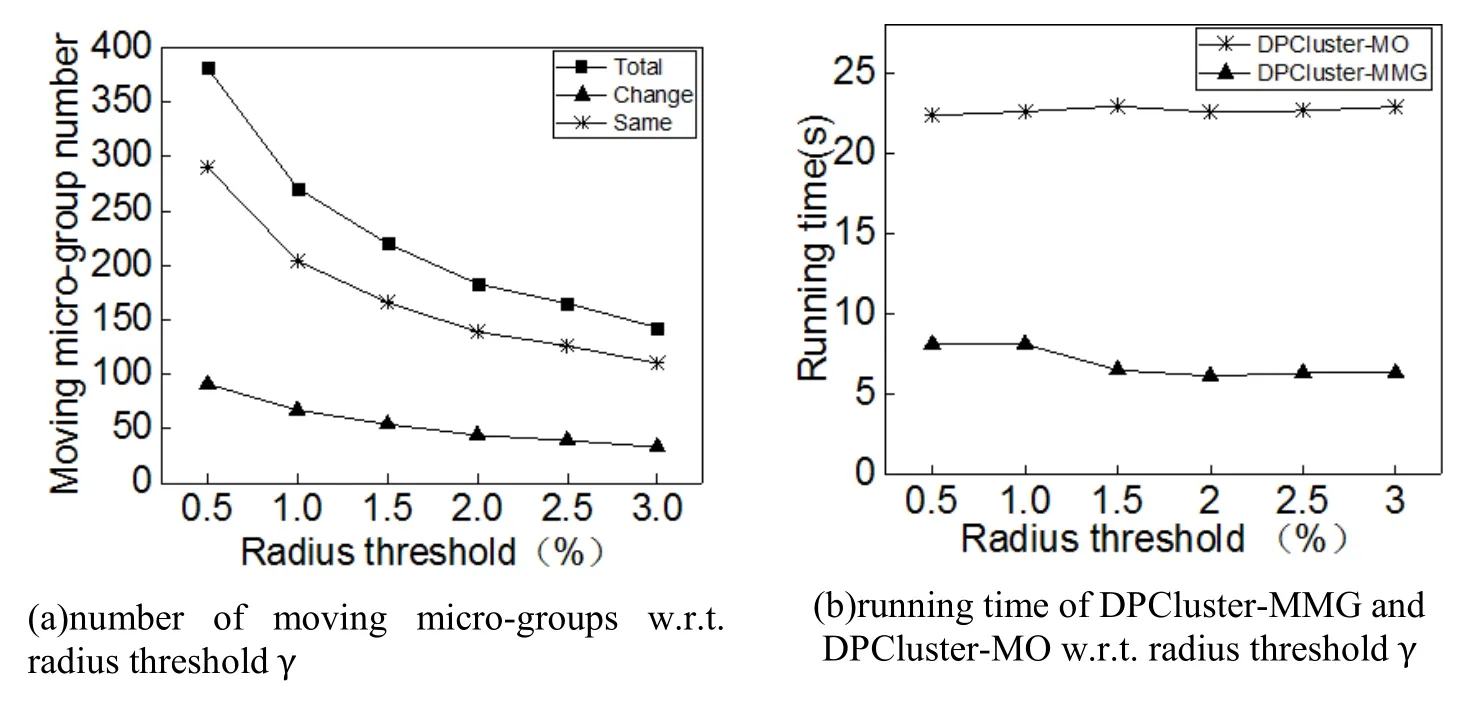
Figure 5:Efficiency analysis of algorithm DPCluster-MMG
5.3.2 Efficiency analysis of algorithm Update-GC
In this section,we analyze the efficiency of Update-GC,a pattern updating algorithm based on intersection operation of clusters.In order to evaluate the effectiveness of the intersection methods proposed in this paper,the execution time of the four methods is calculated.They are traditional intersection method (Naive),intersection method based on related-clusters (RCPR),intersection method based on related-clusters and length pruning rule (RCPR+LPR)and intersection method based on related-cluster,length pruning rule and backward pruning rule (RCPR+LPR+BPR)respectively.As shown in Fig.6(a),as the number of trajectories increases,the running time of four intersection methods is obviously increase.Among them,the traditional intersection method grows exponentially with the increase of trajectory data.The reason is that the increase of trajectory data will lead to the increase of the number of clusters,which results in high intersection overhead.In addition,compared with the traditional method,the intersection method based on the related-cluster increase efficiency by 35%-50%,which proves the effectiveness of our method.For the two pruning rules,intersecting method based on related-cluster and length pruning rule increases efficiency by about 13% than using the intersection method based on the related-clusters alone.However,after adding backward pruning rule,the improvement of efficiency is not obvious.The main reason is that the backward pruning rule requires additional computation to analysis whether the cluster appears in the candidate at previous snapshot.
On the other hand,the size of time window ω in the discovering algorithm also affects the execution time of the intersection operation.As shown in Fig.6(b),with the increasing of the time window size,the execution time of the four intersecting methods is grow accordingly.
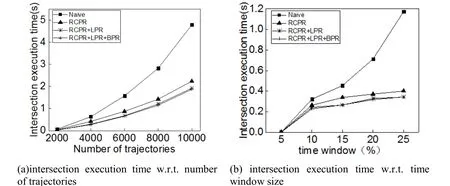
Figure 6:Efficiency analysis of algorithm Update-GC
5.3.3 Efficiency analysis of algorithm DStream-GC
Finally we analyze the efficiency of the GC-Pattern discovery algorithm DStream-GC.Algorithm ClusterGrowth is used to do the comparison.As shown in Fig.7(a),When the number of trajectories is 2000,4000,6000,8000,10000,the running time of the latter is 13,34,39,51,52 times as much as the former,which proves the advantages of the DStream-GC algorithm in trajectory streams processing.
In addition,DStream-GC can be divided into three steps,clustering step,obtaining related-cluster step (O-Step)and updating pattern step based on intersection operation (IStep).Moreover,the clustering step can be further divided into the moving micro-groups updating step (U-Step)and the DP clustering based on moving micro-groups step (CStep).We conduct experiments to calculate the time overhead of each phase and the proportion of time they occupy.As shown in Fig.7(b),as the number of trajectories increases,the execution time of the four phases has significant increases.Among them,the time cost of obtaining related-cluster phase is the smallest,about take 0.3%-0.5% of the total running time,and the execution time of the pattern updating costs 5%-8% of the total time.In contrast,in the traditional intersection operation,the pattern updating operation spends 16%-22% of the total time.In addition,for the clustering operation,the updating time of the moving micro-groups accounts for 60%-80% of the total clustering time,and as the number of trajectories increases,the ratio of the updating time to the total clustering time becomes smaller and smaller,which means the moving micro-group updating algorithm is more suitable for large scale trajectory streams.
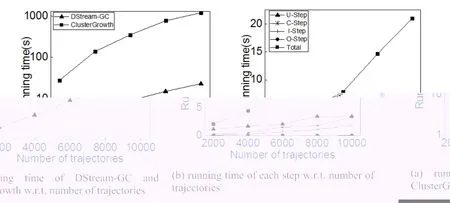
Figure 7:Efficiency analysis of algorithm DStream-GC
6 Conclusion
In this paper,algorithm DStream-GC is proposed to efficiently discover GC-Patterns from trajectory streams.The moving micro-group is proposed to improve the efficiency of clustering and related-cluster is designed to speed up the pattern updating process.We evaluate the proposed algorithms in extensive experiments on two real trajectory datasets.The experiment results demonstrate the effectiveness and efficiency of our algorithms.In the future,we will extend the current discovery algorithm to support other types of moving clusters pattern.
Acknowledgement:This work is supported by the National Natural Science Foundation of China under Grants No.41471371.
杂志排行
Computers Materials&Continua的其它文章
- Stability Analysis of Transfer Alignment Filter Based on the µ Theory
- A Quantum Authorization Management Protocol Based on EPRPairs
- The Algorithm of Chemical Species Analysis for Ab IntioMolecular Dynamics Simulations and Its Application
- Location Privacy in Device-Dependent Location-Based Services:Challenges and Solution
- SWRR:The Link Scheduling Algorithm Based on Weighted Round-Robin
- Analyzing the Structure and Connectivity of Continent-Level Internet Topology
