The Algorithm of Chemical Species Analysis for Ab IntioMolecular Dynamics Simulations and Its Application

Zhiyi Han,Yugai Huang ,Xiaoqiang Xie,Ying Mei and Bin Gu,

Abstract:In ab initio molecular dynamics (AIMD)simulations of chemical reactions,it is important but difficult to identify the chemical species in the trajectory automatically and quickly.In this paper,based on the chemical graph theory,an algorithm for molecular species identification,according to the molecular coordinates and empirical bond length database,is presented.As an example,the chemical species in condensed glycine at room temperature are investigated with our algorithm in detail.The chemical species,including canonical and zwitterionic glycine,their protonated and de-protonated states,and the free protons,are all identified,counted and recorded correctly.Potential applications and further development of the algorithm are also discussed.

Keywords:Chemical species,graph theory,algorithm,AIMD simulations.

1 Introduction

In the last decade,with the lasting improvement of computational simulation capabilities,quantumab initiomolecular dynamics simulations (AIMD)have become more and more important for the multidisciplinary studies of physical,chemical,biological and material science [Chin,Rood,Lin et al.(2000);Kühne (2014);Kohanoff (2006)].One of the great advantages of AIMD simulations is the accurate representation of dynamical changes of chemical bonds,which is crucial for the understanding of micro-dynamics of any chemical reaction [Kühne (2014);Kohanoff (2006)].

In AIMD simulations,the chemical species,e.g.,clusters of atoms with chemical bonding,keep varying.The identification and statistics of specific chemical species emerging in AIMD simulations are routine procedures for most of the reaction studies.For example,in the study initial clustering and aggregation of air pollution particles such as PM2.5 and the cloud condensation nuclei (CCN)from the sources of SO2,ammonia,water vapor,and even criegee intermediates,both the cluster size and isomer structure should be tracked step by step,for the understanding of the growth of the particles in the atmosphere with varying meteorological conditions [Wang,Huang,Gu et al.(2016);Herb,Nadykto and Yu (2011);Zhu,Kumar,Zhong et al.(2016);Myerson and Trout (2013)].In a physiological environment,some bonding (or non-bonding)between specific atoms in protein and DNA are crucial for the survival of a cell [Kohanoff,McAllister,Tribello et al.(2017);Gu,Smyth and Kohanoff (2014)].

However,as far as we know,there is still no report on the algorithm of automatic identification,classification and statistics of the chemical species for AIMD simulations.In literatures,most of the related tasks are accomplished by artificial offline recognition snap by snap after the simulation [Wang,Huang,Gu et al.(2016);Gu,Smyth and Kohanoff (2014)].AIMD is expected to be applied for large scale simulations with over million and more snaps recorded in the trajectory.There needs further guarantee on the unified criteria,accuracy and efficiency in these works.A standard and smart tool is needed for chemical clustering analysis of AIMD simulations [Kühne (2014);Kohanoff (2006)].

In this paper,based on the chemical graph theory [Pietrucci and Andreoni (2011);Dias and Milne (1992)],an identification algorithm for chemical species in AIMD simulation trajectory is presented.In Section 2,the algorithm,e.g.,the manipulation of the connecting matrix (Rc)according to an empirical bonding criteria database,is given in detail.In Section 3,taking the condensed glycine at room temperature as an essential example,the molecular structure variations from complete canonical states to the mixture of zwitterionic and canonical states is studied.Further potential applications and discussions are given at the end of the paper.

2 The chemical species identification algorithm

2.1 The essential problem

In AIMD simulations,the elements of a system are atoms contained in the simulation cell.With the adiabatic approximation,the movements of the valence electrons are described with the time dependent many-body Schröedinger equations (SEs).In practice,the approximations such as Hatree-Fock (HF)and Density Functional Theory (DFT)of SE,are adopted to solve the SEs.The nucleus with core electrons are always regarded as classical mass points and described with the second Newton Law [Kühne (2014)].

In graph theory,a chemical species can be defined as a collection of bonded atoms.For a specific species,any atom is reachable from another one through chemical bond network.The chemical bonds mean stable and strong enough interactions between atoms,ions or molecules.Bonding interactions vary with atom species,local chemical arrangements and macro-circumstances such as temperature and pressure.To figure out the bond connections in the snaps of AIMD trajectory,the bonding criteria,e.g.the standard interatomic distances,should be observed or calculated theoretically.As a starting point,an empirical database of bonding criteria can be established from the experimental measurements with techniques such as X-ray diffraction and NMR methods [Tjandra and Bax (1997)] for typical chemical species.

For AIMD simulations,the coordinates of the atoms are available.The inter-atomic distances can be easily calculated from the atom coordinates.Therefor the connectivity matrix Rc(N×N)of the system,with N atoms,can be defined based on the bonding criteria [Dias and Milne (1992);Pietrucci and Andreoni (2011)].To this end,the essential problem of chemical species identification is how to search and classify the local chemical bonding networks according to their topology information in the MD trajectories accurately and as quick as possible.

2.2 Algorithm and its realization

The flow diagram of our algorithm of chemical species recolonization is shown in Fig.1.Before the configuration of the MD snap is loaded,the initial value of the connectivity matrix Rc(N×N)is set to be zero.Define the distance between the mass centers of a pair of atoms (the i-th and j-th atoms)as r(i,j).If r(i,j)≤r0(i,j),the relevant elements of Rcare set to be Rc(i,j)=Rc(j,i)=1.Here,r0(i,j)is the bonding criteria of the i-th and j-th atoms in the database.For convenience,the diagonal elements Rc(i,i)are all set to be 1.The none-zero elements of this original matrix Rc(org)contains the topology information of current state of the system.

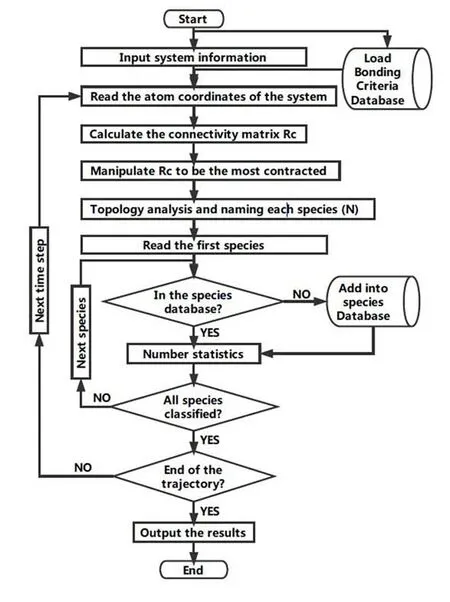
Figure 1:The flow diagram of the chemical species classification and statistics algorithm

To extract the inter-molecule networks and classify the molecule clusters in each MD snap from Rc(org),a serial of manipulations of Rc(N×N)are designed.From the column view of Rc(org),setting the number of the non-zero elements in each (for example,the i-th)column of Rcas m,the i-th atom will directly bond with other (m-1)atoms.If any two columns (for example the i-th and the j-th)have any non-zero matrix element in the same row (for example the k-th row),then these two atoms (the i-th and jth)are indirectly connected through the atom of the non-zero row (the k-th atom).All of the atoms,directly or indirectly,connected with the i-th and the j-th atoms belongs to a local network.The collection of these atoms can be defined as a chemical species.With a serial of operations as:if Rc-ic⋂Rc-jc{0},then Rc-ic=Rc-ic⋃Rc-jcand Rc-ic=0.The networking information can be incorporated into the first column of these atoms,while other following columns will be set as zero.

Through the above column integrations,no crossing link is left between any two non-zero columns.As a result,all of the elements of the upper right corner of the matrix Rcchanges into zero.Each column with non-zero elements represents an isolated chemical species.The number of the non-zero elements in the column equals to the atoms of the specific molecular cluster.The distinct topology of the chemical species can be identified with the value of each element.

Figure 2:Isomers of glycine monomer:a)canonical,b)zwitterion (color online)

In practice,the chemical formula of each species can be represented by the serial of atomic species,each followed by the ordered atom numbers directly connected to that kind of atoms.For more clarity,we take glycine,the simplest amino acid,as example.As shown in Fig.2,the glycine monomer has two states at room temperature with the chemical formula of NH2CH2COOH (canonical)and NH3CH2COO (zwitterion).In our algorithm and program,the topologies of these two isomers are represented by the sequence of atomic species (C-O-N-H).After the name of each atomic species,the numbers of directly connected atoms to these atoms are listed with increasing order.Hence,the canonical and zwitterion are represented as:C34O12N3H11111 and C34O11N4H11111,individually.They topology differences are highlighted by underlined sections.The number of the nearest neighbors of oxygens are {1,2} and {1,1}.For the nitrogen,they are {3} and {4} individually.The time-dependent evolution of all chemical species of glycine in condensed state will be studied in the next section.

In practice,the program of the algorithm has been written in Fortran 90.The trajectory of AIMD simulations in xyz format can be analyzed online and offline,snap by snap.The chemical species are classified automatically.In addition,some optional functions such as coordinates classification and statistics,as shown in Fig.1 are also realized.At present,the code is available via email to the corresponding author.

3 Application:chemical species in amorphous glycine at room temperature

3.1 Basic properties of glycine

Glycine is an excellent example for species analysis because it has great chance to be both locally protonated and de-protonated with proton transferring.In the gas phase,glycine is found in its canonical (neutral)form as shown in Fig.2(left).In aqueous solution,glycine transforms to its zwitterionic form,where a proton transfers from the acid to the amino group as shown in Fig.2(right).Theoretically,the zwitterionic form is more stable than the canonical state by about 7 kcal/mol,with an interconversion barrier around 12 kcal/mol [Leung and Rempe (2005)].

In micro-solvation state,neutral glycine will transform into a zwitterion only after seven water molecules were placed around it [Bachrach (2008)].At room temperature,pure glycine forms a hydrogen-bonded solid,of which three polymorphic crystal structures,α-,β- and γ-,are known [Iitaka (1960)].The polymorphism of glycine makes the molecular structure and degree of crystallinity in condensed state dependent on environmental conditions,presence of additives,etc.

As an application of our algorithm,we performed a long enough AIMDsimulation of glycine in a periodic box,which allows us to gain an understanding of its detailed chemical structures at room temperature.In this work the condensed state glycine is deemed as an amorphous to represent one possible situation under physiological conditions [Shu,Rani,Suryanarayanan et al.(2004);Gu,Smyth and Kohanoff (2014)].

3.2 Simulation details

The initial amorphous sample of the condensed glycine,which contains 32 canonical isomers in a cubic box of 15:05 Å with periodic boundary conditions,was prepared with the molecule editor ATEN [Youngs (2010)].The structure was equilibrated for 1 ns via classical MD simulation using the CHARMM force field [MacKerell,Banavali and Foloppe (2000)] with DL-POLY simulation tool [Smith,Yong and Rodger (2002)].

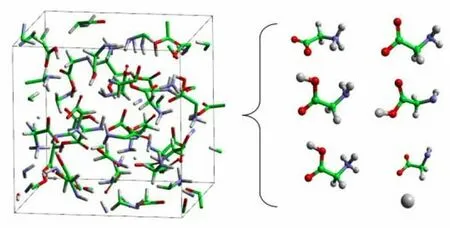
Figure 3:The simulation box which contains 32 glycine molecules (left).The chemical species identified in the AIMD trajectory (right)(color online)

After the classical equilibration,the AIMD simulations were carried out with the quantum module Quickstep (QS)of the open source code CP2K [VandeVondele,Krack,Mohamed et al.(2005)].The AIMD simulations were performed at the PBE [Perdew,Burke and Ernzerhof (1996)] pure DFT functional level theory.Periodic boundary conditions was applied to the Poisson solver.The Goedecker-Teter-Hutter pseudopotentials [Goedecker and Teter (1996)],the TZVP-GTH basis sets,and the PBE [Perdew,Burke and Ernzerhof (1996)] exchange-correlation functional were utilized.The time step of MD simulations is 1 fs.After anab initiooptimization of 500 steps,a product simulation with NVT dynamics at 300 K was carried out for over 15 ps.

3.3 Results and discussions

In the chemical species analysis of the condensed glycine,the bonding criteria are listed as r0(CO)=1.43Å;r0(CN)=1.47Å;r0(CH)=1.09;r0(NH)=1.01Å;r0(OH)=0.96Å.If the distance between two atoms is less than 1.25 times the equilibrium bond length r0,the atoms are bonded.As shown in Fig.3,all of the five possible chemical species in the condensed glycine at room temperature are successfully identified by our program.The four glycine-based species in the sample are:canonical (GlyC),zwitterionic (GlyZ),deprotonated (Gly-H),and protonated (Gly+H).In addition,there exist some free protons (P),which are transferring among the glycine-based molecules.

The numbers of the five species in the simulation box during the AIMD simulation are shown in Fig.4.It can be seen that,during the initial stage of about 4 ps,the system is out of equilibration.The number of canonical glycine keeps decreasing,while the ratios of all other species keep increasing.After the transition period,a dynamical equilibrium is reached in the following simulation.All the fluctuations of the number of each species are no more than 2.In the simulation box,the average number of each glycine-based state is around 8,individually.It means that,the original canonical molecules have changed equally to be the four glycine-based species.Meanwhile,the average number of free protons is around 1.6 in the simulation sample.These dynamically transferring protons promote the transformation among canonical and zwitterionic states of glycine.

Figure 4:Time evolution of the number of molecules species in the sample of amorphous glycine.The bonding criteria is set as R＜1.25R0 (color online)

It is clear that our algorithm of chemical identification and classification for AIMD simulations is quite effective.It should be noticed that the number distribution of molecules of the species depends on the bonding criteria database.As a reference,we recommend the bond length database (https://cccbdb.nist.gov/expbondlengths1.asp)provided by National Institute of Standards and Technology (NIST)for general chemical species identification for AIMD simulations.

4 Conclusions

In this work,we present an algorithm of automatic and quick identification of all chemical species in the trajectory ofab initiomolecular dynamics simulations based on graph theory [Pietrucci and Andreoni (2011);Dias and Milne (1992)].The input data are mainly the atomic coordinates and the general bonding criteria database.The chemical species can be recognized and classified in the dynamics simulations.Our program can be used for both online and offline analysis.It can be widely used for any long-timeab initiomolecular dynamics simulations of molecular clustering and chemical reactions [Myerson and Trout (2013);Wang,Huang,Gu et al.(2016)].

At present,the bonding order parameters have not been taken into consideration in the program.To develop the methods for more complex chemical environments with fast electron transferring and for those atoms with multiple bonding orders,the dynamic bonding criteria should be designed,according to the online calculations of electron density distribution along AIMD simulations [Lu and Chen (2013)].It is the next aim of our project.In addition,some object-orientated functions and interfaces,for more versatile analysis along with chemical species analysis,can also be introduced into the program.

Acknowledgement:The authors thank Dr.Gareth Tribello of Queen’s University Belfast for helpful discussions on the algorithm.This work was partially supported by the program of the Key Laboratory for Aerosol-Cloud-Precipitation of CMA-NUIST (No.KDW1304),the National Natural Science Foundation of China (Grant No.11105075).