基于阻抗的电动汽车并网逆变器的稳定性分析

宋绍剑 刘延扬 刘斌 宋春宁

摘 要：针对电动汽车向电网馈送能量（V2G）時，车载并网逆变器与电网之间的交互作用引起的并网逆变器不稳定和电能质量问题，首先采用基于阻抗的稳定分析方法研究电动汽车并网逆变器与配电网之间的交互作用;其次根据阻抗比奈奎斯特判据分析配电网阻抗对并网逆变器稳定性的影响，采用谐波线性化方法建立考虑锁相环的单相LCL型并网逆变器小信号阻抗模型，并提出一种基于电压前馈的并网逆变器自适应相位补偿控制策略，以便确保其具有足够的稳定裕度。最后通过仿真验证了所提控制策略的有效性。

关键词：电动汽车;并网逆变器;阻抗;稳定分析;电压前馈控制

中图分类号：TM 464

文献标志码：A

文章编号：1007-449X（2019）04-0111-09

0 引 言

随着近年来电动汽车的快速普及，电动汽车市场占有率的日益扩大，电动汽车作为一种可移动的储能设备可接入微网（或低压配电网），形成“车—网”互动的概念。通过对电动汽车进行合理调度，可以充分发挥其对电网的削峰填谷、旋转备用和支撑系统等功能[1]。不过，随着大规模的电动汽车通过并网逆变器将电能反馈回电网，此时的微网（或低压配电网）中将存在大量的并网逆变器。为了提高逆变器抑制谐波的效果，通常车载并网逆变器一般采用LCL型滤波的拓扑结构。由于采用LCL滤波器的并网逆变器自身存在两个高频谐振频率点;同时，大量车载并网逆变器通过公共连接点（points of common connection，PCC）以并联方式连接到电网中，各个并网逆变器通过LCL滤波回路之间交互作用产生关联与耦合，使PCC处的电网阻抗发生变化。而PCC处的阻抗变化又将可能导致并网逆变器的谐振，产生大量谐波，使并网电流质量大幅下降，届时电动汽车不仅不能实现其应有的功能，反之会降低系统电能质量[2-3]。

为了研究解决并网逆变器在PCC处与电网交互而引发的谐波振荡问题，一般需要建立其谐波小信号模型。目前国内外并网逆变器的建模及稳定性分析方法大致可分为两类。其中一类是将并网逆变器和PCC处的网络阻抗作为一个整体，对整个系统进行稳定性分析，但这类方法由于控制参数与电网阻抗间的耦合作用，而模型变得十分复杂;另外一类则是对并网逆变器输出阻抗进行单独建模，结合PCC处阻抗信息，再利用基于阻抗的稳定分析方法分析并网逆变器的稳定性。稳定分析的理论工具包括奈奎斯特稳定判据、根轨迹法、Bode图分析等，此类方法被证明是分析并网逆变器谐波振荡产生机理的有效方法之一[4-8]。

在对并网逆变器进行阻抗建模时，由于传统的平均建模方法针对的是工作点固定的直流变换电路，而交流变换电路不存在像直流变换电路那样固定的直流工作点，传统小信号方法不能直接用于交流变换电路。为此，文献[15]提出了一种基于谐波线性化的阻抗建模方法。与传统建模方法相比，采用该方法得到的并网逆变器的输出阻抗模型可直接通过硬件扫描验证，也可直接用于研究解决并网逆变器在PCC处的谐波振荡问题中。参考文献[9-10]分别推导建立了单相和三相并网逆变器的基于谐波线性化的阻抗模型，并通过控制锁相环带宽来提高系统在电网变化时的稳定性。但目前针对电动汽车并网逆变器稳定分析的研究相对较少，大部分还集中在研究其电路拓扑结构和控制器优化。

本文采用基于阻抗的分析方法对电动汽车并网逆变器的稳定性问题展开研究。首先搭建了两级式电动汽车并网逆变器仿真模型，然后推导了电动汽车并网逆变器在考虑锁相环情况下基于谐波线性化的输出阻抗模型，并在此基础上利用基于阻抗的稳定性判据分析了电网阻抗、电动汽车电池电压对电动汽车并网逆变器稳定性的影响;最后提出了一种相对简单有效的自适应动态补偿并网逆变器输出阻抗相位的电压前馈控制策略，提高了电动汽车并网逆变器在电网阻抗增加时的自适应能力。

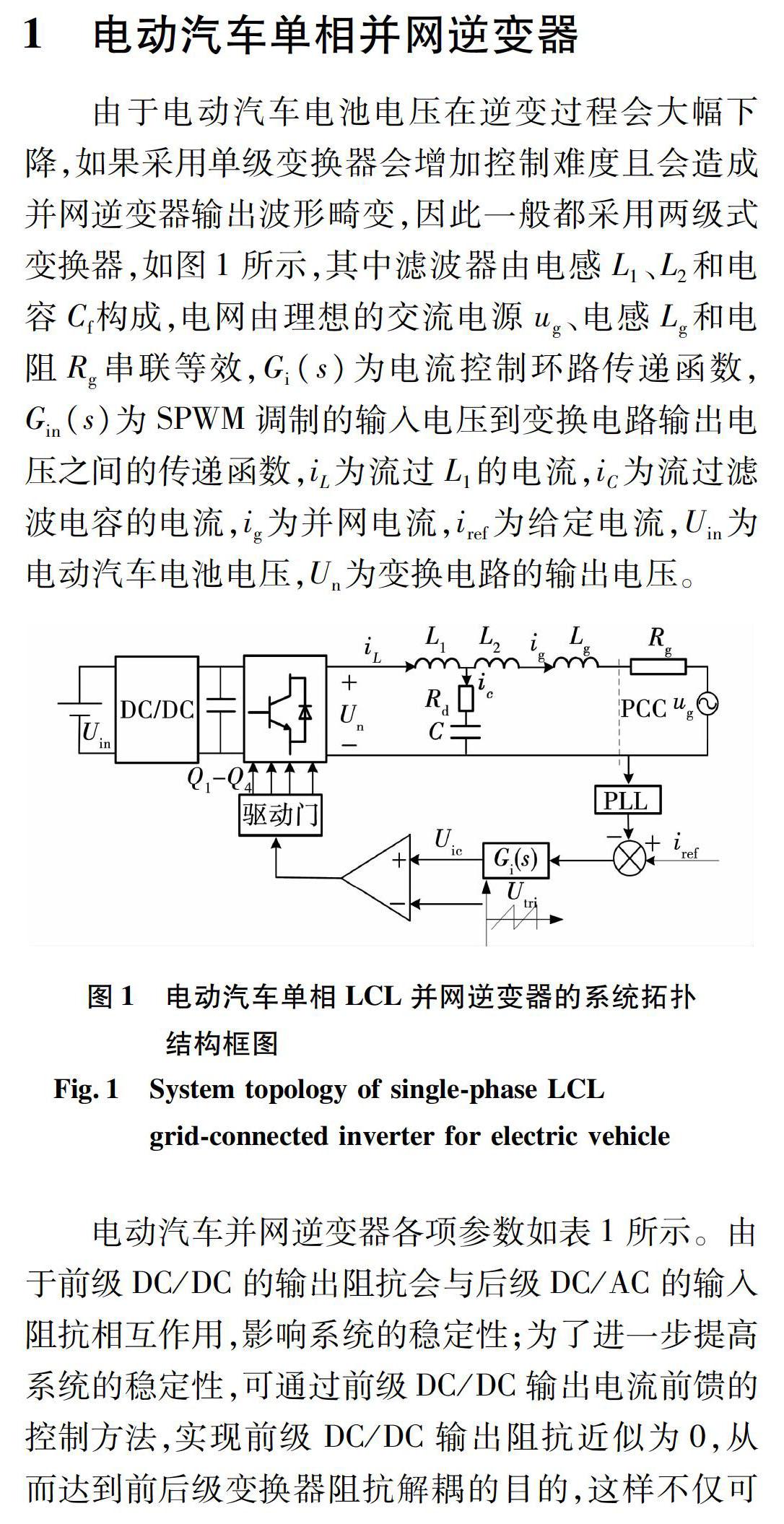
1 电动汽车单相并网逆变器

由于电动汽车电池电压在逆变过程会大幅下降，如果采用单级变换器会增加控制难度且会造成并网逆变器输出波形畸变，因此一般都采用两级式变换器，如图1所示，其中滤波器由电感L1、L2和电容Cf构成，电网由理想的交流电源ug、电感Lg和电阻Rg串联等效，Gi（s）为电流控制环路传递函数，Gin（s）为SPWM调制的输入电压到变换电路输出电压之间的传递函数，iL为流过L1的电流，iC为流过滤波电容的电流，ig为并网电流，iref为给定电流，Uin为电动汽车电池电压，Un为变换电路的输出电压。

电动汽车并网逆变器各项参数如表1所示。由于前级DC/DC的输出阻抗会与后级DC/AC的输入阻抗相互作用，影响系统的稳定性;为了进一步提高系统的稳定性，可通过前级DC/DC输出电流前馈的控制方法，实现前级DC/DC输出阻抗近似为0，从而达到前后级变换器阻抗解耦的目的，这样不仅可以提高整个系统的稳定性，且整个系统的输出阻抗可近似为后级DC/AC的输出阻抗[11]，因此本文所提到的电动汽车并网逆变器输出阻抗均指后级DC/AC的输出阻抗。

2 电动汽车单相并网逆变器稳定性分析

2.1 基于阻抗的并网逆变器稳定性判据

电动汽车通过并网逆变器把电能反馈回电网，其并网逆变器一般被控制为电流源，因此并网系统可以等效为一个诺顿等效电路，即如图2所示：并网逆变器可等效为一个理想电流源与逆变器输出阻抗并联;电网可等效为一个理想电压源与电网阻抗串联。其中ZO为电动汽车并网逆变器输出阻抗，Zg为电网阻抗。

由图2的小信号等效电路，根据电路叠加定理可求出输出电流为

为了进一步分析输出电流Ig的稳定性，假设电网电压Ug在不接并网逆变器时是稳定的;输出电流Ig在电网阻抗Zg为0时稳定。基于该假设，则Is（s）-Ug（s）Zo（s）是稳定的，因此输出电流Ig的稳定性取决于11+Zg/Zo，该式相当于一个非单位负反馈系统，可知当电网阻抗和逆变器输出阻抗比值满足奈奎斯特稳定性判据时11+Zg/Zo稳定，则逆变器输出电流稳定。

2.2 电动汽车电池电压对并网逆变器的影响

当电动汽车并网逆变器采用单级机构时，在逆变上网过程中，当电网阻抗不变，而电池电压下降会对并网逆变器的稳定性造成一定的影响，其表现为：降低式（5）中的调制波到变换电路的传递函数KPWM，从而降低电动汽车并网逆变器的输出阻抗，从基于阻抗的并网逆变器稳定性判据可知，当电网阻抗不变，并网逆变器输出阻抗降低，会导致两者在幅频域交截点降低，低频附近的谐波将得以放大，系统将出现不稳定，影响并网电流质量。如图3为电池电压为350 V和400 V时的逆变器输出阻抗和电网阻抗比较，从图中可知当电池电压下降，逆变器输出阻抗在低频段会降低，与电网阻抗相等时的频率也在降低，这会导致系统的稳定性下降，如图4所示的不同电池电压条件下电动汽车并网逆变器输出波形，当电池电压为400 V时，电动汽车并网逆变器输出波形正常;但当电池电压下降到300 V时，电动汽车并网逆变器输出波形畸变严重，产生大量谐波。但若逆变器采用两级结构，则可忽略其电池电压降低对逆变器的影响。

2.3 电网阻抗对电动汽车并网逆变器稳定性的影响

图5为不同电网阻抗条件下，仿真模型输出的电流电压波形，由圖可知当电网为理想电网时（电网阻抗约为0）输出电流电压是稳定的，随着电网逐渐变弱（电网阻抗变大），电动汽车并网逆变器输出的电流电压波形变得不稳定。

为了进一步定性分析电网阻抗与逆变器输出阻抗比值与稳定性的关系，画出不同电网阻抗条件下Zg/Zo的奈奎斯特曲线如图6所示。对比分可知当Zg为0.5 mH时，系统相位裕度为85°，表明系统是稳定的，但Zg为5 mH时，系统相位裕度降低到5°，表明这时系统是不稳定，这和仿真波形分析也相吻合。

为了进一步定量分析电网阻抗与逆变器稳定性的关系，画出不同电网阻抗与逆变器输出阻抗曲线，如图7所示。

分析可知，当Zg为0.5 mH时，在2.2 kHz处电网阻抗超过逆变器输出阻抗，此时所对应的相位裕度为85°左右，则此交点对系统稳定性并不产生影响;但随着串接电网阻抗逐渐增加，电网阻抗与并网逆变器输出阻抗比值的截止频率（即Zg/Zo=1）逐渐往低频移动。例如，当Zg为5 mH时，电网阻抗在500 Hz左右超过逆变器输出阻抗，相对应的系统相位裕度为5°左右，这表明逆变器与电网阻抗间相互作用产生较高谐振导致系统在截止频率附近（500 Hz）的谐波得以放大，使得逆变器的输出电流不稳定;当电网阻抗进一步增大，再如当Zg增大到10 mH时，电网阻抗在400 Hz左右超过逆变器输出阻抗，此时系统所对应的相位裕度更低，系统将更不稳定。

3 单相并网逆变器系统的输出阻抗模型

3.1 并网逆变器输出阻抗模型

由于整个单相并网逆变系统的输出阻抗可等效于后级DC/AC的输出阻抗，因此只需推导后级DC/AC的输出阻抗，单相并网逆变器系统的控制结构框图如图8所示，其中KPWM=Uin/Utri为调制波到开关电路的传递函数，Utri代表三角载波的幅值，GPLL（s）为锁相环的传递函数，Hv为网侧电压反馈系数，取值为1/311。

根据系统框图可写出节点电流和回路电压方程为

当考虑锁相环时，电动汽车并网逆变器输出阻抗为

3.2 基于谐波线性化的锁相环环路模型

由于锁相环是并网逆变器必需环节且其特性对逆变器影响很大，因此建立基于谐波线性化的锁相环路模型，以分析其对并网逆变器稳定性的影响是必需的。本文仿真模型中锁相环采用的是单相同步旋转坐标系法（SRF-PLL），其控制框图如图9所示，其中ω0、为基波角频率和功率因数。

3.3 含锁相环的逆变器输出阻抗模型

将3.2节中推导出的基于谐波线性化的锁相环模型加入3.1节中逆变器输出阻抗模型中，推导出逆变器基于谐波线性化的阻抗模型，同时可画出并网逆变器的输出阻抗波特图如图10所示。

对比可知，锁相环对逆变器输出阻抗的幅值影响很小，但对逆变器输出阻抗在基频附近的相位影响较大。此外，通过在仿真模型中在电网侧加入不同频率的扰动以获得逆变器在不同频率下的实际输出阻抗幅值、相位（图10中用叉表示）。从图中可知仿真模型的输出阻抗特性与数学阻抗模型特性基本吻合，从而也验证了基于谐波线性化的数学阻抗模型的准确性。同时针对于实际模型会存在参数误差而影响控制策略性能的情况，可采用如上提到的在电网侧加入不同频率的扰动以获得逆变器在不同频率下的实际输出阻抗幅值、相位以代替逆变器的数学阻抗模型，从而克服实际模型存在参数误差而影响控制策略性能的情况。

4 电压前馈控制策略

由以上分析可知，电网阻抗影响逆变器稳定性的根本原因是：随着电网阻抗的增加，使Zg/Zo的截止频率fc（Zg/Zo=1）降低，导致Zg/Zo=1处的相位裕度降低，从而导致系统不稳定。为了提高系统的稳定性，可采用在一种电压前馈策略在截止频率处补偿系统相位的，使其在截止频率附近相位裕度达到30°～60°以上，从而提高系统稳定性。

根据超前补偿原则，首先假定相位补偿函数为

5 控制策略验证

5.1 仿真验证

基于电压前馈的自适应相位补偿控制策略的具体实施框图如图11、图12所示：首先利用在电流给定处叠加PRBS（pseudo-random binary sequence）序列，实时测量电网阻抗;然后计算出Zg/Zo的截止频率、相位裕度，并由此得出需在截止频率处对电动汽车并网逆变器输出阻抗补偿的相位大小，最后依据式（14）～式（17）和式（19）计算出电压前馈函数，与电流环控制信号叠加在一起生成SPWM模块的控制信号，最终实现对并网逆变器的相位补偿，提高其在电网阻抗增大时的自适应能力。

以Zg为5 mH时为例，根据最小相位补偿原则，设定补偿的相位角为30°，具体参数计算过程如下：

1）根据图7读出，当Zg为5 mH时，截止频率为500 Hz，则ωm=2πfc=3 140 rad/s;2）依据m=30°，然后根据式（13）、式（14）则可计算出m=5 437，n=1 812;3）根据式（15）则可算出k=2;4）把计算出的参数代入式（17），则可计算出电压前馈参数。

根据计算结果可画出加入电压前馈后逆变器输出阻抗曲线如图13所示，其中Z′o、Zo表示加入和未加入电压前馈时的逆变器输出阻抗，对比分析可知，加入电压前馈后基本不改变截止频率（500 Hz）处逆变器输出阻抗的幅值，但其相位却提高了30°左右，由图14的奈奎斯特曲线同样也可看出其相位裕度提高了30°，从而提高了系统在Zg为5 mH时的稳定性。

5.2 实验验证

为了验证控制策略有效性，在具体参数如表1所示的仿真模型上进行了实验验证，输出波形如图15、图16所示，输出电流波形的谐波分析如图17、图18所示，由图16可知在加入电压前馈前，当Zg为5 mH时系统输出电流不稳定，由图17可知，造成系统不稳定的其主要原因为第10次（500 Hz）谐波的影响;施加电压前馈控制策略后，系统输出电流趋于稳定，由图18也可以看出，在施加电压前馈控制策略后，第10次谐波明显被抑制，表明施加的控制策略能有效抑制截止频率附近由于并网逆变器与电网阻抗相互作用产生的谐波，提高电动汽车并网逆变器对电网的自适应能力。

6 结 论

本文以搭建的电动汽车并网逆变器的仿真模型和推导的基于谐波线性的逆变器阻抗模型为基础较深入的研究了电网阻抗对单相LCL电动汽车并网逆变器稳定性的影响;同时根据并网逆变器稳定性判据，得出随着串接的电网阻抗逐渐增加，电网阻抗与逆变器输出阻抗比值的截止频率逐渐降低，系统相位裕度也逐渐降低，从而导致系统逐渐趋于不稳定;针对电网阻抗与逆变器之间相互作用问题提出了一种自适应动态补偿相位的电压前馈控制策略，实现了在截止频率处对并网逆变器的相位补偿，提高了系统稳定性，并且其设计过程相对简单，对电动汽车并网逆变器的稳定性控制具有一定意义。同时针对于实际模型会存在参数误差而影响控制策略性能的情况，可采用第3.3节提到的在电网侧加入不同频率的扰动以获得逆变器在不同频率下的实际输出阻抗幅值、相位以代替逆变器的数学阻抗模型，从而克服实际模型存在参数误差而影响控制策略性能的情况。

参 考 文 献：

[1]高赐威，张亮，电动汽车充电对电网影响的综述[J].电网技术， 2011， 35（2）：127.

GAO Ciwei， ZHANG Liang.A survey of influence of electrics vehicle charging on power grid[J].Power System Technology，2011， 35（2）：127.

[2] YANG S，LEI Q，PENG F Z，et al.A robust control scheme for grid-connected voltage-source inverters[J]. IEEE Transactions on Industrial Electromcs， 2010，58（1）：202.

[3] WANG X ， BLAABJERG F ， LOH P C . An impedance based stability analysis method for paralleled voltage source converters[C]// 2014 International Power Electronics Conference， May 18-21，2014，Hiroshima，Japan.2014：1529-1535.

[4] 訐德志，汪飞，毛华龙，等，多并网逆变器与电网的谐波交互建模与分[J].中国电机工程学报， 2013， 33（12）：64.

XU Dezhi， WANG Fei， MAO Hualong，et al.Modeling and analysis of harmonic interaction between multiple grid-connected inverters and the utility grid[J].Proceedings of the CSEE， 2013， 33（12）：64.

[5] Céspedes， Mauricio， SUN J . Modeling and mitigation of harmonic resonance between wind turbines and the grid[C]// Energy Conversion Congress & Exposition，Sep. 17-22，2011，Phoenix，America.2011： 2109-2116.

[6] LIU H， SUN J. Impedance-based stability analysis of VSC-based HVDC systems[C]// Control & Modeling for Power Electronics，June 23-26，2013，Salt Lake City， UT， USA.2013：1-8.

[7] 李小强， 伍小杰，耿乙文，等. 感性电网阻抗下三相光伏逆变器稳定性分析[J].中国电机工程学报， 2014， 34（18）：2906.

LI Xiaoqiang， WU Xiaojie， GENG Yiwen， et al. Stability analysis of three-phase PV inverter under inductive grid impedance condition[J]. Proceedings of the CSEE， 2014， 34（18）：2906.

[8] CHEN X， SUN J. A study of renewable energy system harmonic resonance based on a DG test-bed[C]// Applied Power Electronics Conference and Exposition （APEC）， Mar. 6-11，2011，Fort Worth，America.2011： 995-1002.

[9] 吴恒，阮新波，杨东升.弱电网条件下锁相环对LCL型并网逆变器稳定性的影响研究及锁相环参数设计[J].中国电机工程学报， 2014， 34（30）：5259.

WU Heng， RUAN Xinbo， YANG Dongsheng. Research on the stability caused by phase-locked loop for LCL-type grid-connected inverter in weak grid condition[J].Proceedings of the CSEE， 2014， 34（30）：5259.

[10] 王赟程，陈新，陈杰. 基于谐波线性化的三相LCL型并网逆变器正负序阻抗建模分析[J]. 中国电机工程学报， 2016， 36（7）： 1915.

WANG Yuncheng， CHEN Xin， CHEN Jie，et al.Analysis of positive-sequence and negative-sequence impedance modeling of three-phase LCL-type grid-connected inverters based on harmonic linearization[J].Proceedings of the CSEE，2016， 36（7）： 1915.

[11] REDL R， SOKAL N O. Near-optimum dynamic regulation of DC-DC converters using feed-forward of output current and input voltage with current-mode control [J]. IEEE Transactions on Power Electronics， 1986，1（3）： 181.

[12] CESPEDES M，SUN Jian.Impedance modeling and analysis of grid-connected voltage source converters[J].IEEE Trans. on Power Electronics，2014，29（3）：1254.

[13] 王萍， 蔡蒙蒙， 王尉. 基于自适应陷波滤波器的有源阻尼控制方法[J]. 电机与控制学报， 2015， 19（9）：108.

WANG Ping， CAI Mengmeng， WANG Wei. Active damping control method based on adaptive notch filter [J]. Proceedings of the Chinese Society of Electrical Engineering and Control， 2015， 19（9）： 108.

[14] 徐玉琴， 马焕均. 基于改进下垂控制的逆变器并联运行技术[J]. 电力系统保护与控制， 2015（7）：103.

XU Yuqin， MA Huanjun. Parallel operation technology of inverters based on improved droop control[J]. Power System Protection and Control， 2015（7）：103.

[15] SUN Jian，BING Zhonghui，KARIMI K J.Input impedance modeling of multipulse rectifiers by harmonic linearization[J].IEEE Trans. on Power Electronics，2009，24（12）：2812.

[16] 金亮亮， 周荔丹， 姚钢， 等. 适用于并网逆变器的新型LCL 滤波器[J]. 电力系统保护与控制， 2016， 44（11）：12.

JIN Liangliang， ZHOU Lidan， YAO Gang，et al. A novel LCL filter adopted in grid-connected inverter[J]. Power System Protection and Control， 2016， 44（11）：12.

[17] SUN Jian.Impedance-based stability criterion for gridconnected inverters[J].IEEE Trans. on Power Electronics，2011（11）：3075.

[18] 易映萍， 罗海， 胡四全. 小功率光伏并网逆变器控制策略的研究[J]. 電力系统保护与控制， 2016（4）：64.

YI Yingping， LUO Hai， HU Siquan. Study on control scheme based on low-power photovoltaic grid-connected inverter[J]. Power System Protection and Control， 2016（4）：64.

[19] SUN Jian. Small-signal methods for AC distributed power systems-a review[J].IEEE Trans. on Power Electronics，2009， 24（11）：2545.

[20] 田鹏，宣文华，牛益国. 基于陷波控制的 LCL 型光伏并网逆变器谐波谐振抑制研究[J]. 电力系统保护与控制， 2016， 44（14）：82.

TIAN Peng， XUAN Wenhua， NIU Yiguo. Suppression of harmonic resonance for photovoltaic grid-connected inverter with LCL filter based on notch filter control[J]. Power System Protection and Control， 2016， 44（14）：82.

[21] 中国电力科学研究院.Q/GDW 480-2010分布式电源接入电网技术规定[S].北京：国家电网公司，2010.

（编辑：刘琳琳）