带位置误差校正的开关磁阻电机电流梯度法

曾辉 杨向宇

摘 要：电流梯度法是一种通用性强，操作简单的无位置传感器技术。该方法对相电流进行低通滤波时导致相位后移，且转速越大，位置检测偏差越大，限制了适用的转速范围。对此采用零相移滤波方法，计算上一周波相电流因滤波产生的相移角，并對当前时刻输出的位置角进行补偿，提高位置检测精确度。分析了PWM控制方式下的相电流波形频谱，以确定合适的滤波截止频率。实验结果表明所提方法将转速对位置检测精确度的影响降低了86%，扩大了电流梯度法适用的转速范围。

关键词：无位置传感器控制;零相移滤波器;电流梯度法;开关磁阻电机; 位置检测

中图分类号：TM 352

文献标志码：A

文章编号：1007-449X（2019）04-0083-07

0 引 言

开关磁阻电机具有结构简单、坚固、高效、造价低等优点，是一种广受关注，具有良好发展前景的电机。开关磁阻电机在正常运行时，需要实时的转子位置信息进行换相，产生连续转矩。目前一般采用光电式、电磁式、霍尔传感器或轴编码器检测转子位置。对位置传感器的依赖增加了系统成本、降低了系统可靠性、加大了系统体积、限制了应用范围，极大地削弱了开关磁阻电机本体相对其他电机更适合工作在恶劣环境的优势。为克服这些缺点，有必要发展开关磁阻电机的无位置传感器控制技术。

现有的无位置传感器技术有电流斩波法[1]、脉冲注入法[2-3]、调制解调法[4]、互感法[5]、磁链法[6]、电感法[7]、观测器法[8]。这些方法都需要预知电机的数学模型，通用性不强，难以实用化。有学者基于开关磁阻电机的电感曲线特征，提出了电流梯度法[9-10]，通过检测相电流峰值点获取定转子凸极开始重合位置，即理想电感模型中的最小电感末端位置。文献[11]提出使用电流梯度法检测最小电感始端位置。此类方法不依赖电机模型，无需进行磁链的存储、查表、复杂的模型计算等操作，适用于任何常规结构的开关磁阻电机，且实现简单，具有较强实用性与通用性。然而，现有的电流梯度法须对相电流依次进行滤波、求导、再次滤波、过零比较等操作，而实时的滤波操作必然导致相位后移，使得检测到的位置信息出现延迟，形成误差，且转速越高误差越大。位置检测误差明显影响对电机的控制性能，同时严重限制了该方法适用的转速范围。因此，有必要解决滤波产生的位置检测误差的问题。

对此提出了带角度补偿机制的开关磁阻电机特殊位置检测方法，通过对上一周期的相电流进行零相移滤波，计算实时滤波操作产生的相移角度，以此对位置角进行补偿，修正因实时滤波产生的检测误差。该方法可提高位置检测精确度，提高无位置传感器控制性能，扩大适用的转速范围。

1 电流梯度法的位置检测误差

电流梯度法通过求取相电流的导数过零点确定峰值出现时刻，以此检测转子位置。以四相8/6结构的SRM为例，如图1电流波形所示，受PWM载波及电磁噪声影响，在求取电流导数前，须对相电流进行滤波，以得到平滑的电流波形，截止频率通常为PWM载波频率的1/2。如图1 di/dt波形所示，为避免误判，通常在对电流导数进行过零比较前，须对电流导数进行滤波，截止频率通常为PWM载波频率的1/2。图1所示方波上升沿为输出的位置信号，显然，由于两次滤波操作导致相位后移，输出的位置信号滞后于实际相电流出现峰值的时刻，该延迟可用转子角度Δθ 描述，在此例中Δθ=3°，Δθ即为电流梯度法误差的主要来源。

Δθ 的大小随转速与负载而变化，图2为仿真得到的Δθ与转速和负载的关系，由图可知，转速越高，位置检测误差越大。

由式（2）和式（6）可知，滤波前后信号相位差为零，增益为低通滤波器增益的平方，该特点适用于所有频率的正弦信号。需要注意的是，ZPSF只适合对已知的信号进行离线分析，不适用于信号的实时处理。理论上任何实时的滤波操作都将产生相移。

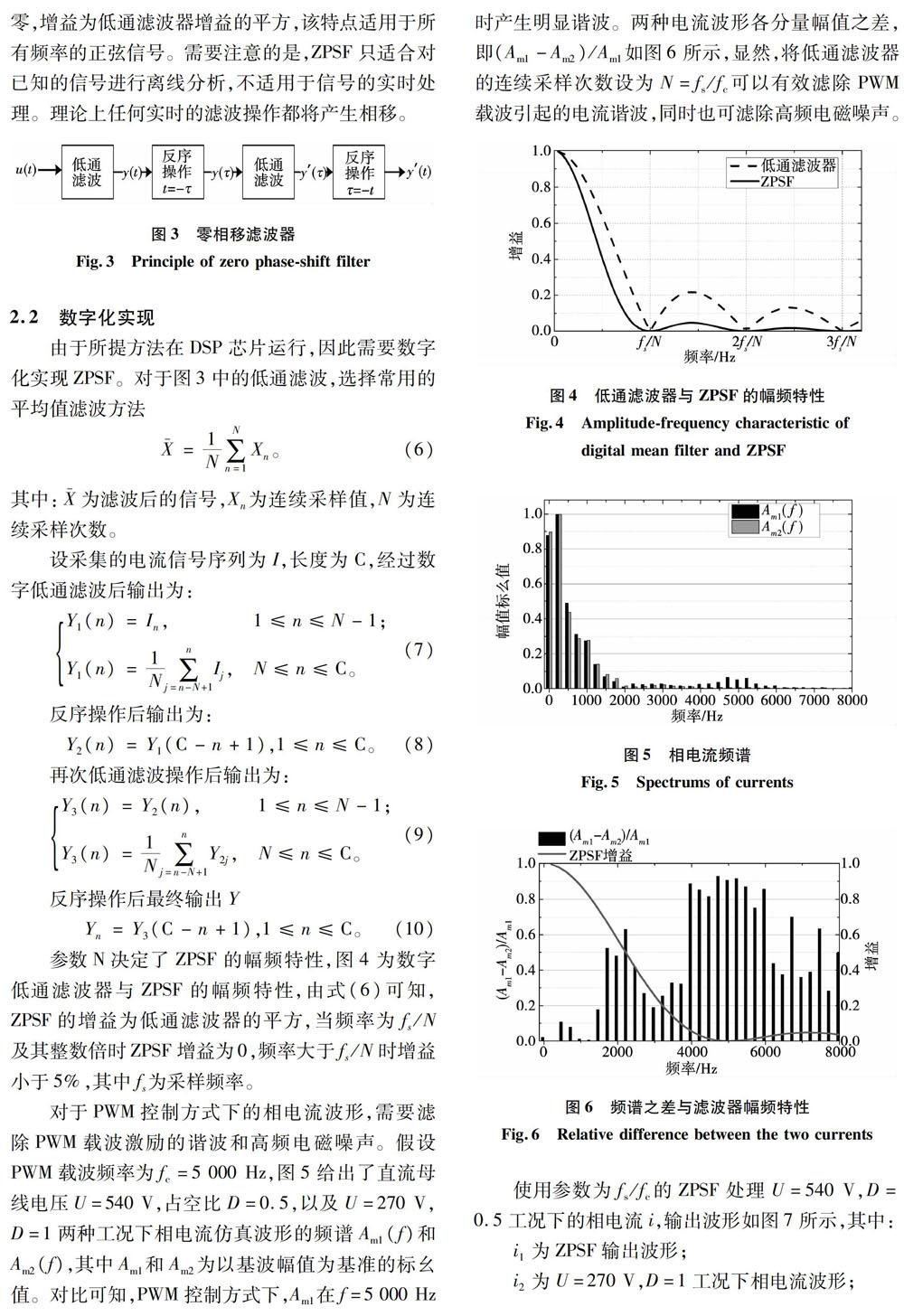
2.2 数字化实现

由于所提方法在DSP芯片运行，因此需要数字化实现ZPSF。对于图3中的低通滤波，选择常用的平均值滤波方法

参数N决定了ZPSF的幅频特性，图4为数字低通滤波器与ZPSF的幅频特性，由式（6）可知，ZPSF的增益为低通滤波器的平方，当频率为fs/N及其整数倍时ZPSF增益为0，频率大于fs/N时增益小于5%，其中fs为采样频率。

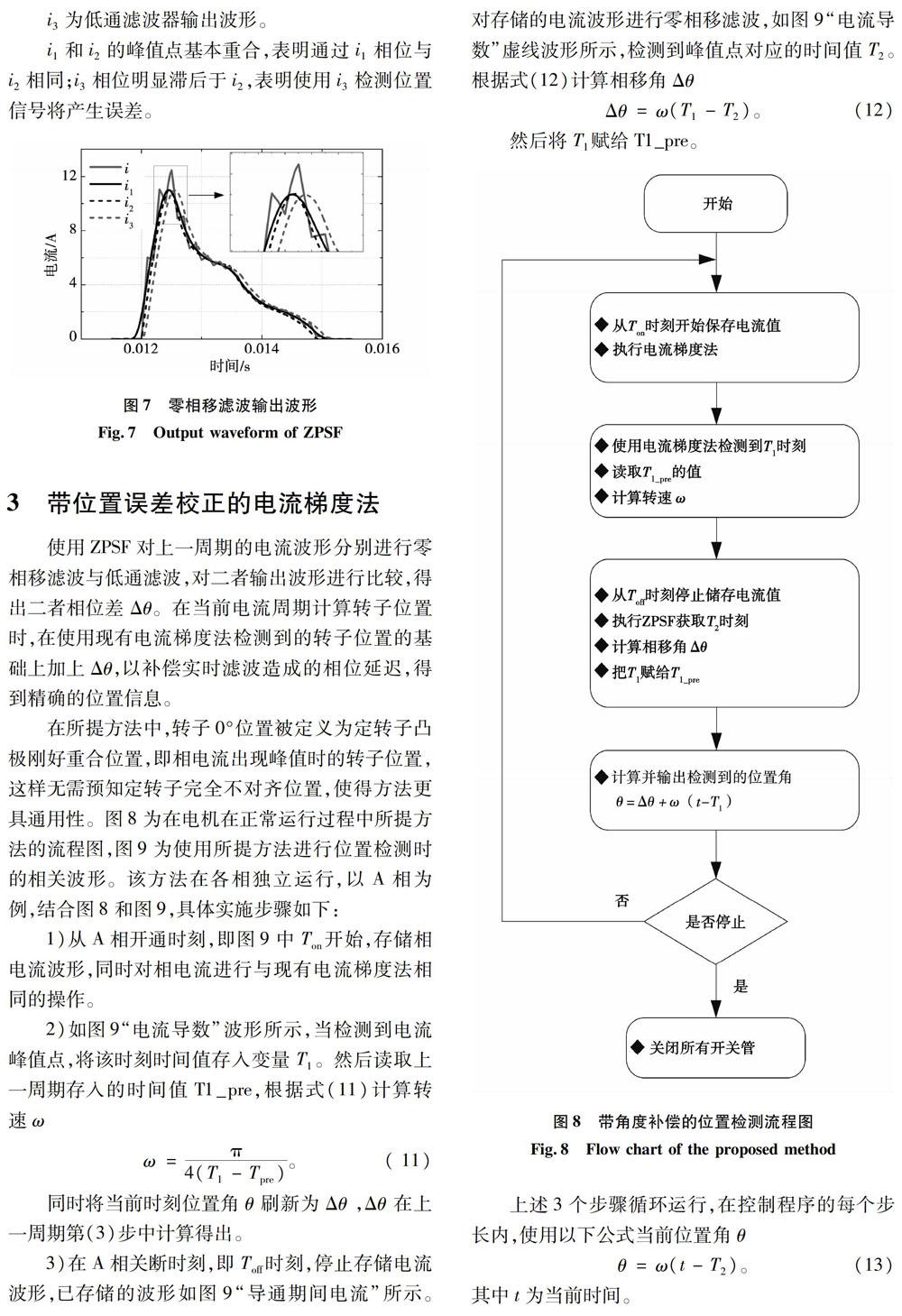
对于PWM控制方式下的相电流波形，需要滤除PWM载波激励的谐波和高频电磁噪声。假设PWM载波频率为fc=5 000 Hz，图5给出了直流母线电压U=540 V，占空比D=0.5，以及U=270 V，D=1两种工况下相电流仿真波形的频谱Am1（f）和Am2（f），其中Am1和Am2为以基波幅值为基准的标幺值。对比可知，PWM控制方式下，Am1在f=5 000 Hz时产生明显谐波。两种电流波形各分量幅值之差，即（Am1-Am2）/Am1如图6所示，显然，将低通滤波器的连续采样次数设为N=fs/fc可以有效滤除PWM载波引起的电流谐波，同时也可滤除高频电磁噪声。

使用参数为fs/fc的ZPSF处理U=540 V，D=0.5工况下的相电流i，输出波形如图7所示，其中：

i1为ZPSF输出波形;

i2为U=270 V，D=1工况下相电流波形;

i3为低通滤波器输出波形。

i1和i2的峰值点基本重合，表明通过i1相位与i2相同;i3相位明显滞后于i2，表明使用i3检测位置信号将产生误差。

3 带位置误差校正的电流梯度法

使用ZPSF对上一周期的电流波形分别进行零相移滤波与低通滤波，对二者输出波形进行比较，得出二者相位差Δθ。在当前电流周期计算转子位置时，在使用现有电流梯度法检测到的转子位置的基础上加上Δθ，以补偿实时滤波造成的相位延迟，得到精确的位置信息。

在所提方法中，轉子0°位置被定义为定转子凸极刚好重合位置，即相电流出现峰值时的转子位置，这样无需预知定转子完全不对齐位置，使得方法更具通用性。图8为在电机在正常运行过程中所提方法的流程图，图9为使用所提方法进行位置检测时的相关波形。该方法在各相独立运行，以A相为例，结合图8和图9，具体实施步骤如下：

1）从A相开通时刻，即图9中Ton开始，存储相电流波形，同时对相电流进行与现有电流梯度法相同的操作。

2）如图9“电流导数”波形所示，当检测到电流峰值点，将该时刻时间值存入变量T1。然后读取上一周期存入的时间值T1_pre，根据式（11）计算转速ω

同时将当前时刻位置角θ 刷新为Δθ ，Δθ 在上一周期第（3）步中计算得出。

3）在A相关断时刻，即Toff时刻，停止存储电流波形，已存储的波形如图9“导通期间电流”所示。 对存储的电流波形进行零相移滤波，如图9“电流导数”虚线波形所示，检测到峰值点对应的时间值T2。根据式（12）计算相移角Δθ

4 实验验证

实验平台示意图如图10所示，所用样机为一台四相8/6结构SRM，功率7.5 kW;轴编码器为10位增量式编码器，用于评估位置检测精确度;霍尔型电流传感器采集相电流，输出给控制器，用于实现无位置传感器控制;控制器为高速数据处理芯片DSP28335;功率变换器为不对称半桥结构。

控制器运行无位置传感器控制程序，输出开关信号给功率变换器，实现换相。示波器采集三路信号用于观察位置检测精确度。CH1通道为电流传感器输出的相电流;CH2通道为所提方法检测到的位置信号，当检测到电流峰值时电平翻转;CH3通道为检测到电流峰值时编码器输出的位置角，该数字信号通过模数转换接入示波器。

图11（a）～图11（d）为负载为10 N·m，转速分别为1 000 r/min、2 000 r/min、3 000 r/min、4 000 r/min时的实测波形。

通过观察相电流峰值点与位置信号可知，检测到的位置信号与峰值点时刻基本重合。随着转速增加，检测到的位置信号对应的转子位置有变大趋势，但幅度很小。由图11（c）可知，当转速为3 000 r/min时检测到的位置信号对应的转子位置出现一定范围的波动，这是因为在PWM控制方式下，对于不同相电流周期，在绕组开通时刻PWM载波相位不同，导致相电流波形出现差异，影响峰值检测的结果。当转速较高时该影响尤其明显;然而，当占空比接近1时，该影响较小，因此如图11（d）所示，转速为4 000 r/min时，PWM占空比为0.96，每个周期的相电流波形基本相同，则检测到的峰值点对应的转子位置基本一致。

对于理想的位置检测方法，检测到的位置角应不受工况影响，即输出角度与转速与负载无关。然而，受诸如控制器运行速度限制，电机局部磁饱和，采样误差等多因素的影响，实际检测到的转子位置并不保持恒定，其波动范围可用于评估位置检测方法的精确度。为评估传统电流梯度法与所提方法的位置检测精度，实验给出了两种方法获取的电流峰值点对应的转子位置角，结果如图12所示。由图可知，随着转速的增加，传统电流梯度法检测到的θs明显变大，而所提方法变化较小;随着负载增加，两种方法检测到的θs都有所变大，且变化幅度接近。

5 结 论

由于滤波操作不可避免产生相位后移，现有电流梯度法输出的位置信号滞后于定转子凸极开始重合时刻，造成检测误差，且转速越高误差越大。使用零相移滤波方法可计算实时滤波操作产生的相移角度，对现有方法检测到的位置角进行补偿。实验结果表明，该方法可有效解决上述问题，显著降低转速对检测结果的影响，有利于拓展其适用的转速范围。然而，受凸极边角局部磁饱和影响，在不同负载工况下，检测到的定转子凸极开始重合位置并不完全相同，使得本方法仍然存在一定误差，有必要进行进一步的研究。

参 考 文 献：

[1]PANDA S K，AMARATUNGA G A J. Waveform detection technique for indirect rotor-position sensing of switched-reluctance motor drives. I. Analysis[J]. IEE Proceedings of Electric Power Applications，1993， 140（1）：80.

[2] JUN C，ZHIQUAN D. Sensorless control of switched reluctance motor based on phase inductance vectors[J]. IEEE Transactions on Power Electronics.2012， 27（7）：3410.

[3] PASQUESOONE G，MIKAIL R，HUSIN I. Position estimation at starting and lower speed in three-phase switched reluctance machines using pulse injection and two thresholds[J]. IEEE Transactions on Industry Applications.2011， 47（4）：1724.

[4] SUESH G，FAHIMI B，EHSANI M.Improvement of the accuracy and speed range in sensorless control of switched reluctance motors[C]//Applied Power Electronics Conference and Exposition， 1998：771.

[5] YE J，BILGIN B，EMADI A.Elimination of mutual flux effect on rotor position estimation of switched reluctance motor drives considering magnetic saturation[J]. IEEE Transactions on Power Electronics.2015， 30（2）：532.

[6] 张磊， 刘闯， 管旻珺，等. 基于特征位置磁链开关磁阻电机无位置传感器技术[J]. 南京航空航天大學学报，2013，（05）：671.

ZHANG Lei， LIU Chuang， GUAN Minjun，et al. Sensorless research on switched reluctance motor based on special position simplified flux method[J]. Journal of Nanjing University of Aeronautics & Astronautics，2013，（05）：671.

[7] 周竟成， 王晓琳， 邓智泉，等.开关磁阻电机的电感分区式无位置传感器技术[J]. 电工技术学报，2012，（07）：34.

ZHOU Jingcheng， WANG Xiaolin， DENG Zhiquan，et al. The position sensorless technology of switched reluctance motor based on the regional comparison of three-phase inductance[J]. Transactions of China Electrotechnical Society，2012， （07）：34.

[8] KHALIL A，UNDERWOOD S，HUSAIN I，et al. Four-quadrant pulse injection and sliding-mode-observer-based sensorless operation of a switched reluctance machine over entire speed range including zero speed[J]. IEEE Transactions on Industry Applications，2007， 43（3）：714.

[9] BATEMAN C J，MECROW B C，CLOTHIER A C，et al.Sensorless operation of an ultra-high-speed switched reluctance machine[J]. IEEE Transactions on Industry Applications.2010， 46（6）：2329.

[10] GALLEGOS-LOPEZ G，KJAER P C，MILLER T J E. A new sensorless method for switched reluctance motor drives[J]. IEEE Transactions on Industry Applications，1998，34（4）：832.

[11] 曾辉， 陈昊， 徐阳. 基于分步续流法的开关磁阻电机无位置传感器控制[J]. 电工技术学报，2013，（07）：124.

ZENG Hui， CHEN Hao， XU Yang.Sensorless control of switched reluctace motor based on fractional step freewheeling methods[J]. Transactions of China Electrotechnical Society，2013，（07）：124.

（编辑：贾志超）