立足生本 自然生长 提升素养

马敏

【学习目标】

通过游戏活动，感悟生活中描述物体位置的重要性和必要性;通过丰富的现实情境和数学情境，感受确定位置的方法，感受数量变化和位置变化的联系，发展数形结合意识、形象思维能力和数学应用能力。

【学习重、难点】

重点：掌握并运用坐标法、方向角加距离法确定物体位置;了解运用经纬法、区域定位法确定物体位置。

难点：把实际问题转化为数学问题——数学建模意识的培养;体悟数量变化与位置变化的联系——数形结合意识的培养。

【设计思路】

运用自主、合作探究、实验的教学模式，学生通过对生活中和数学中确定位置不同方法的探究，经历数学的抽象过程，感悟数学的应用价值，体验成功的喜悦和合作的快乐。课前让学生自己去查找經纬线、区域定位等资料，参与到课堂的全过程。整节课设计以“开放、合作、探究”为主线，给学生充分的思考的空间和表现的机会，让学生在一个较为宽松的氛围中去体验数学学习带来的乐趣。

【教学流程】

活动一：对号入座

师：欢迎同学们走进今天的课堂，不过你得先拿着课前老师发给你的座位号卡，找到你的座位。

（注：此处25张座位号卡，其中设计3个特殊的座位号，一个是只写有数字3，另外两张分别写有4，5和5，4，其余学生的座位号写明“第×行，第×列”或“第×列，第×行”。）

问题1. 问手持数字“3”卡的学生：你怎么一直在教室里徘徊？直到最后你才犹豫地坐在了这个位置上？

生：我的卡片与其他同学的不一样，只有1个数字3，我不知道是第3行还是第3列，更不知道是哪个位置，最后看到就剩这个位置，它正好在第3行（列）上，所以我才坐下的。

师：原来只有1个数字的座位号让你无法确定自己的位置。你能告诉同学们你现在所坐的座位号应该是什么吗？

问题2. 问手持“4，5”和“5，4”卡的学生：你们怎么站在了同一个位置上？

生1：我们的卡上都写着数字4和5，但我认为我的是第4列第5行，而他的应该是第5列第4行，所以这个位置应该是我的。

生2：我认为他说的不对，其他同学的都明确是第×行第×列，而我们的上面只有2个数字，那么它们一定是1个是行数，1个是列数，所以我认为我的也可以是第4列第5行。

师：你们卡上的数字顺序不同，让你们产生了不同的理解，一个同学认为第1个数是列数，第2个数是行数，而另一个同学则相反。

问题3. 假如我们约定“列数在前，行数在后”，那这个位置应该属于谁呢？如果老师再提供一个位置，应该放在哪儿呢？

（设计意图：从学生的生活经验出发，创设情境，提出问题，激发学生学习数学的兴趣。让学生通过亲身经历从具体情境中发现数学问题，进而解决问题的全过程，感受现实世界中蕴含的大量的数学信息。）

问题4. 怎样才能准确确定教室里座位的位置？行数和列数的先后顺序对位置有影响吗？如果老师用（3，2）表示第3行第2列的同学座位号，那么你的座位号应该如何表示呢？

问题5. 生活中还有类似这样确定物体位置的实例吗？

（设计意图：围绕确定教室中学生的座位这个问题进行讨论，让学生体会确定位置时需要两个数据，并且感受到这两个数据的顺序的重要性，同时为学生后续学习平面直角坐标系奠定基础。最后1个问题具有开放性，根据学生的回答可能涉及3个数据确定位置的方法，教师适时加以说明。）

活动二： 经纬法表示位置

问题1. 老师绘制了一张平面化的经纬图，请你说说连云港市的地理位置。利用这张图，你还能说说济南的位置吗？

问题2. 如果告诉你一组经度和纬度，你能说出是哪个城市吗？

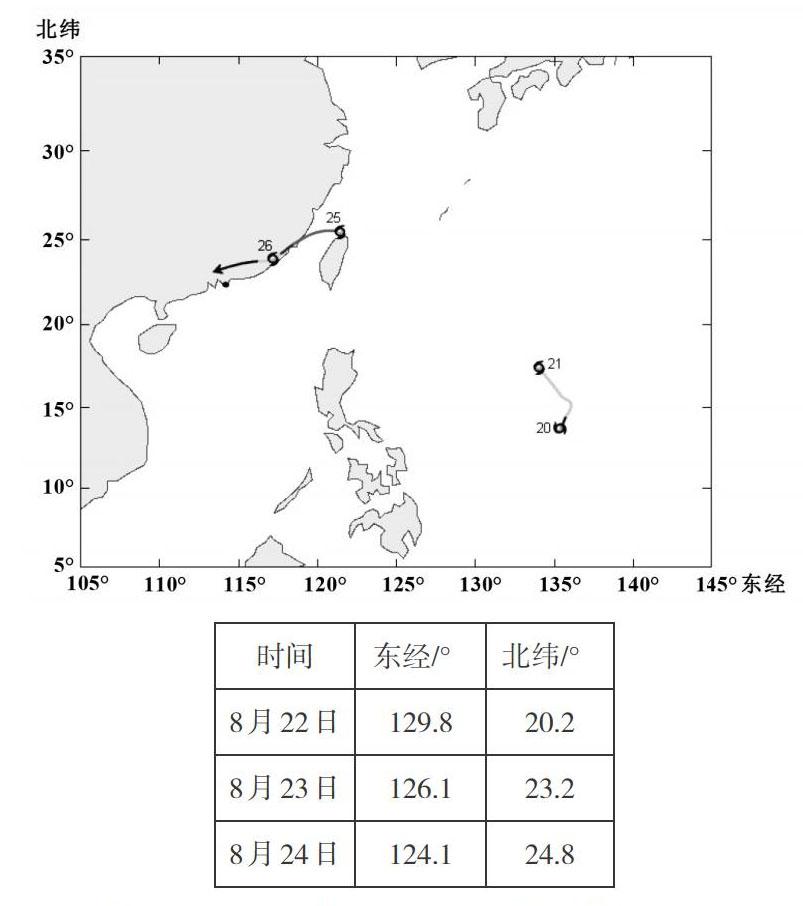
问题3. 每年的夏秋季是台风的多发时期，沿海城市的人们都会比较关注每一次台风的运动过程是否会对自己的城市造成影响，请根据表中数据，绘制一张经纬网图，并用平滑的曲线表示台风中心移动路径。

（设计意图：学生经历运用所学知识寻找实际背景的过程，在自主探究中熟悉了确定位置的第二种方法：经纬法。同时让学生体悟由点找坐标以及由坐标确定点的方法。）

活动三：区域定位法

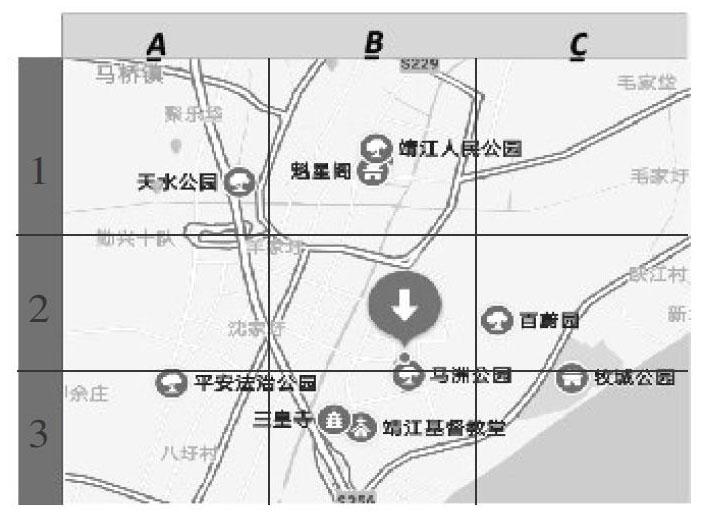
问题1. 如果你的一位外地朋友来我们美丽的靖江，为了你的朋友查找景点方便，你可以仿照经纬网将我市的主要旅游景点划分成区域。你如何介绍马洲公园所在的区域？在这一区域还有哪些景点呢？

问题2. 生活中有类似确定物体位置的例子吗？

（设计意图：问题1暗含区域定位法;学生看到问题2，根据经验都会想到大型演出或者活动等，也是先分区域再定位置，实质就是利用区域定位和有序数对确定物体位置。）

活动四：利用方向角和距离定位

问题1. 你的朋友在参观完梅兰芳纪念馆之后，准备到另一著名景点——城隍庙去看看。如果现在只知道城隍庙在梅兰芳纪念馆的北偏西55°方向，你能确定它的位置吗？

问题2. 如果老师再告诉你梅兰芳纪念馆与城隍庙之间的图上距离为5cm。请你利用上图，找到城隍庙的位置。

问题3. 请用同样的方法，描述一下凤城河风景区相对于梅兰芳纪念馆的位置（画图并测量），并请同学们思考梅兰芳纪念馆相对于凤城河风景区的位置。

（设计意图：此种确定位置的方法是本节课的难点，学生需要在教师的指导下自主操作完成。首先要找到观测点、建立方向标，然后测量目标与观测点之间的距离，从而找到用“方向角+距离”确定物体位置的方法。）

活动五： 实践应用

问题1. 根据下列提示，绘制一张老师的家乡连云港的市区主要风景区示意图。

（1）学校位于（1，2）;

（2）花果山乡的位置为（4，5）;

（3）花果山风景区在花果山乡的正东面4km;

（4）云龙涧风景区位于（9，6）;

（5）东磊风景区在花果山风景区的南偏东45°方向，同时在云龙涧风景区南偏西45°方向;

（6）从云龙涧风景区向右走4格，再向上走5格到达新亚欧大陆桥东端起点。

问题2. 在你所绘的图上，苏马湾和孔望山的位置如何表示？

（设计意图：设置此应用问题，让学生综合运用“坐标法”和“两条射线交点法”这两种确定物体位置的重要方法，旨在突出重点，突破難点，提高学生综合运用知识的能力。）

活动六：数学中位置的确定

问题1. l是线段BC的垂直平分线，在点A沿直线l自上而下运动的过程中，图中的一些线段的长短、角的大小也随之变化。

（1）∠BAC的大小是如何变化的？

（2）点A在什么位置时，△ABC是等边三角形？是直角三角形？

（设计意图：先操作观察。再结合教师的几何画板演示，引导学生关注数量变化与位置变化关系在数学中的体现。同时在此基础上，引导学生自己提出问题，以增强学生“发现问题和提出问题”“分析问题和解决问题”的能力。）

活动七：反思感悟

问题1. 确定平面内物体的位置有哪些常见的方法？每种方法需要几个数据？生活中如此，数学中呢？说说你的看法。

问题2. 这节课我们共同探讨了在平面内确定物体位置的几种方法，它们一般需要两个数据，可以是一对有序数对，可以是方向角和距离，还可以用两条线的交点，或通过区域来确定物体的位置。在我们生活的空间中的物体的位置是否也可以用数字确定？希望同学们课后可以利用今天所学的知识找到答案。

问题3. 如果在刚才的连云港的景区示意图中，向左走3格，再向下走6格，到达东海温泉，请问东海温泉的位置如何表示呢？

（设计意图：三个问题层层深入，问题1是回顾，回忆确定平面内物体位置的方法，感悟数量变化与位置变化的关系。问题2是从二维位置确定到三维位置确定，让思维升华。问题3是让学生在思维冲突中促进思考，为下一节课平面直角坐标系做好铺垫。这样的有层次的问题会让学生的学习从课内向课外延伸，让学习不再是片段化的知识点，而是整体建构下的生长的学、有需要的学。）

教学反思：

作为本章的第一节，本节课承载着平面直角坐标系的铺垫功能。5个“动手做数学”的活动：对号入座→查找地图→景点分区→测量定位→绘制旅游图。以确定连云港市的主要旅游景点的位置为“主线”，以找座位、测量、绘制旅游图等“动手做数学”活动为“路径”，引导学生对生活中确定物体位置的不同方法进行探究，让学生经历数学的抽象过程（即数学化的过程），帮助学生感悟数学的应用价值，构建充满生机的活力课堂。

本节课抓住学生已有的经验，“对号入座”是基于学生看电影的经验，表示城市的地理位置基于学生阅读地图的经验，确定两个景区相对位置基于学生测量的经验，绘制景区示意图基于学生获取信息的经验等。这些细微的经验是学生每天都触及和不断累积的，因此，这节课中的“做数学”对学生而言是力所能及的。而当这些点滴经验经历“数学化”的过程之后，就变为方法经验（确定物体位置的方法）。

在本节内容中，所承载的主要核心素养为直观想象、数学抽象。如从学生的现实世界出发，通过寻找座位、确定城市地理位置、描出台风中心位置的移动路径、两个景区的相对位置、绘制主要景区示意图等活动，帮助学生数学地理解确定物体位置的不同方法。在这些活动的背后，其实都在做同一件事，也就是反复帮助学生进行“抽象”，让学生经历数学化的过程。比如说，“对号入座”可以帮助学生抽象出“行与列两条线的交点”，从而确定一个同学的座位;“城市地理位置”查找帮助学生抽象“经线和纬线的交点”，从而确定一个城市（这里的城市也抽象成一个点）的位置;“两个景区相对位置”的确定可以帮助学生抽象出“方向角的射线和距离确定的点”，从而可以确定相对位置;绘制市区主要风景区示意图，则更是数学化的过程，其实就是平面直角坐标系的“雏形”。应该说，经上述的抽象过程，后续的平面直角坐标系的学习则是水到渠成之事了。

（作者单位：江苏省连云港市教育局教研室）