具有不等式路径约束的微分代数方程系统的动态优化
2019-06-11孙燕张弛路兴龙王靖戈付俊
孙燕 张弛 路兴龙 王靖戈 付俊
动态优化是约束中含有微分或差分方程的一类数学规划问题[1−3],其广泛存在于电力系统[4−5]、石油化工[6−7]、生物工程[8−9]、清洁能源[10−11]等. 目前在化工过程中基于常微分方程模型的动态优化问题不仅涉及微分方程,还包括代数方程约束,这样的系统统称为微分代数系统.此外,实际的流程工业过程中,需要某些状态变量或控制变量的函数在其全部运行过程中或部分运行时间内不能超过约束的设定值,来保证工业过程的质量和安全,这就需要考虑具有不等式路径约束的动态优化问题.
动态优化问题(Dynamic optimization problem,DOP)的数值求解算法通常分为直接法[12−13]和间接法[14−15].间接法通过求解原问题的最优性条件(即必要条件),间接地获得原问题的最优解.但是对于相对复杂的问题,比如包含不等式约束的最优控制问题,由于状态变量或者控制变量在约束中存在,求解极为困难[16].此外,复杂的非线性系统最优性条件很难被定义,且两点边值问题的求解过程中收敛域可能很小[17].直接法是通过对控制变量离散化,即控制向量参数化[18](Control vector parameterization,CVP),或控制与状态变量同时离散化,即正交配置(Orthogonal collocation,OC),将无限维的最优控制问题转化为有限维的非线性最优化问题.由于OC方法的计算复杂度较高,本文采用CVP方法.
针对具有不等式路径约束的微分代数方程(Differential-algebraic equations,DAE)系统的动态优化问题,采用直接或间接法对其进行转化后,仍需要对等式路径约束和不等式路径约束进行处理.胡云卿等将等式路径约束进行微分[19],将原问题转化为具有不等式的常微分方程(Ordinary differential equations,ODE)动态优化问题,再使用基于ODE的动态优化方法进行处理,但是DAE到ODE的转化过程中需要考虑初值条件的相容性,并且无法在理论上证明有关解的存在性和唯一性[20],此外,当约束中变量的幂较高或者变量间耦合程度较高的情况下是不可行的.Pontryagin等将等式路径约束转化为两点边值问题[21]进行求解,该方法需要增加约束条件,增加了求解难度.Fabien将等式约束转化为终点约束[22],这样会导致问题的维数变得很大,需要对转化后的问题进行降维处理.所以间接地处理DAE中的等式路径约束会引起一系列的问题,因此本文采用后向差分法(Backward differentiation formula,BDF)[23]直接求解DAE.
对于不等式路径约束,文献[24]采用多重打靶(Multiple shooting,MS)法,将不等式路径约束转化为分段的点约束,每次打靶均需要给出对应打靶分段内该点约束涉及的控制变量和各状态变量合理的范围,各变量段间的连续还需要一个合适的系数保证,不然很难得到理想的结果.文献[25]对不等式路径约束的积极与否进行判断,若不等式路径约束为积极约束,则结合微分方程在DAE求解器中进行求解,否则不考虑该不积极约束;不等式路径约束为积极约束时,DAE阶次可能很高,所以该方法对DAE求解器要求较高.Jacobson等提出的松弛变量法[26],通过增加松弛变量将不等式路径约束转化为相应的等式路径约束,但是这种方法难以处理不等式路径约束数比控制变量数多的问题;Vassiliadis等[27]通过离散化将约束项在问题时间约束段内选择有限个内点进行离散化,通过惩罚函数法将约束违反的积分设为0来保证约束的无违反,但是此方法可能会在NLP问题中引进较多的约束条件;Floudas提出的凸函数近似法[28]主要应用于静态系统,Chachuat等[29]将其改进应用在动态系统的最优控制上,此方法求得的数值解虽然可以严格满足不等式路径约束,但算法复杂度较高;Rehbock等提出的精确罚函数法[30]能够成功求解具有不等式路径约束的复杂最优控制问题[31],该方法虽然在算法复杂度上有所改善但是不能严格满足不等式约束,且约束违反程度不能确定;Liu等[32−33]提出了一种新颖的光滑化精确惩罚函数法,将不等式路径约束转化为一个光滑化惩罚项加到目标函数中,将问题转变成一个无约束优化问题;由于目标函数表达式会因不等式约束的违反程度随时间而改变,所以如何获取问题转化后目标函数的梯度信息是一个难点.2005年Chen在之前的CVP-OC混合方法基础上进一步提出了有限收敛法[34],问题初始求解时不考虑不等式路径约束的最优控制问题,将初始所得解做为初始解以此优化原问题,这样可以使得优化过程得以优化.然而该方法受限于带有不等式路径约束的ODE动态优化问题,对于带有不等式路径约束的非0阶DAE动态系统的适用性有待探究.
因此,本文针对具有不等式路径约束的DAE系统的动态优化问题,采用只对控制变量进行参数化的CVP方法,将无限维的DOP转化为有限维的DOP,仍然保留系统的动态特性.通过分点离散化方法将不等式路径约束转化为有限的内点约束进行处理,设计了在指定的路径约束违反容忍度下通过有限步迭代获得KKT(Karush Kuhn Tucker)最优点的算法.然后利用BDF方法求解DAE方程组,再采用序列二次规划法(Sequential quadratic programming,SQP)获得满足不等式路径约束的最优解.最后将该算法应用在工业化工问题中,仿真结果表明了该算法可以获得最优控制轨迹并有着良好的路径约束效果及收敛性.
本文的主要贡献如下:
1)采用后向差分法直接求解DAE,避免将DAE化为ODE的过程中会产生的解的相容性、维数增加等前文所述问题.2)所采用的处理路径约束的方法不会改变目标函数的结构形式.并且可以在指定路径约束违反的容忍度的条件下,经过有限步迭代得到最优解.
本文结构如下:第1节对具有不等式路径约束的DAE系统的最优控制问题进行描述.第2节阐述本文所采用的求解动态优化问题和处理不等式路径约束的算法.第3节将算法应用于工业化工问题.最后对本文所做工作进行了总结并提出了对未来可以改进的方面进行了展望.
1 问题描述
本文考虑的具有不等式路径约束的DAE系统的最优控制问题,根据Biegler[35]给出的动态优化问题描述形式添加不等式路径约束条件,记为P1,给出数学描述如下:
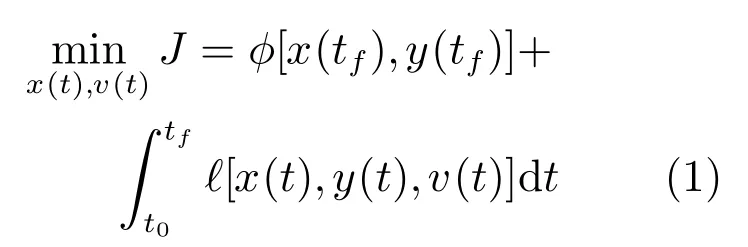
s.t.
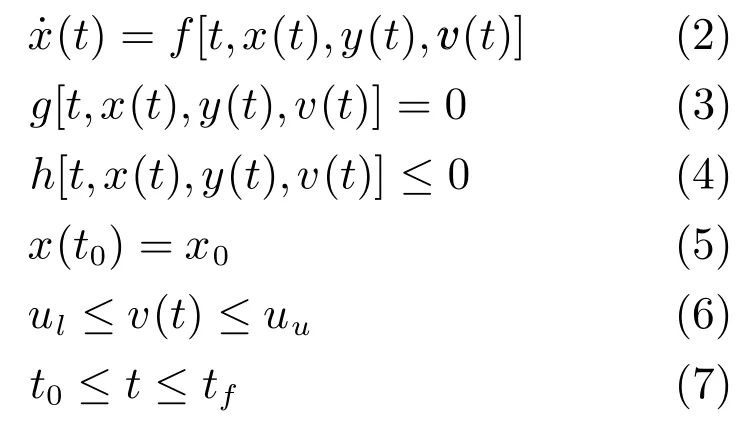
其中,x(t)∈Rnx是状态变量,y(t)∈Rny是代数变量,v(t)∈Rnu是控制变量且上下边界约束分别为ul和uu,这些变量都是时间标量t∈[t0,tf]的函数;动态过程开始时刻t0和结束时刻tf都是固定的;动态系统特性由常微分方程(2)组成;其初始可行状态为xx0;动态优化问题的最优解需要满足等式路径约束(3)、不等式路径约束(4);目标函数式(1)由终值项φ[x(tf),y(tf)]和被积函数为‘[t,x(t),y(t),v(t)]的积分项组成.其中,等式路径约束(3)和常微分方程(2)组成DAE.为不失一般性,假设这里的DAE对各变量均有连续二阶偏导数,且index为1.
这些DAE系统具有更大的灵活性:可以是线性的也可以是非线性的;不等式路径约束(4)可以有多个,若有多个不等式路径约束,其处理方法同(4).
该最优控制问题可以简单描述为:在可行初始状态(5)条件下,寻找最优的控制轨迹v∗(t),使得式(2)和式(3)描述的系统满足约束(4),且使得目标函数(1)的值最小.
2 主要结果
本文针对具有不等式路径约束的DAE系统的最优控制问题,首先利用CVP技术将无限维的DOP转化为有限维的DOP,将原问题转化为仍保留系统动态特性的具有不等式路径约束的DOP.对于系统的动态方程,采用BDF直接求解,避免了将DAE转化为ODE或两点边值问题.利用逐点离散法处理不等式路径约束,将不等式约束在违反处转化为有限的点约束,在有限步的迭代下,得到满足用户指定的路径约束违反容忍度的KKT最优点.算法的主要结构如图1所示.
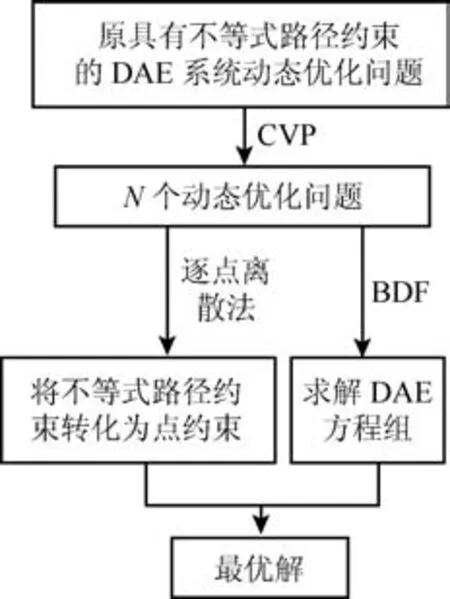
图1 算法主要结构图Fig.1 Structure diagram of the algorithm
本节首先简要介绍了控制向量参数化方法及其处理后得到的有限维的DOP.然后在逐点离散法中,路径约束被转化为点约束的形式,同时给出了不等式路径约束的DAE系统最优控制问题的具体求解算法.并给出了分点离散法收敛性的证明.
2.1 控制向量参数化
CVP是求解动态优化问题的一种重要策略.CVP方法的核心思想[36]是:利用基函数将控制变量进行参数化,将原无限维最优控制问题转化为一个含有动态过程的有限维优化问题后,再用传统的DOP求解方法进行求解.即将控制向量v(t)被离散为n段而状态变量保持连续,每个时间分段内用带参数的多项式(如常数、线性或二次多项式).关于控制变量参数化方法的收敛性,文献[37−38]都进行了相应的证明.
首先不考虑不等式路径约束,将动态优化问题的时间域[t0,tf]划分为N个控制阶段,
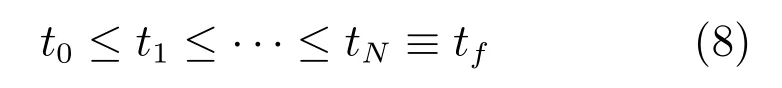
在某一时间分段[tk−1,tk],k=1,2,···,N内,根据函数逼近理论,控制变量可以表示为低阶多项式参数依赖的表达形式,
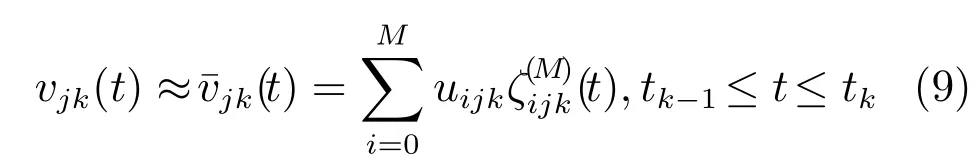
其中,j表示原问题有 1,2,···,j,···,nu个控制变量,为多项式基函数,M为基函数阶数.实际计算和应用中控制向量的参数化可以有多种参数依赖形式,如图2所示常用的有分段常量逼近策略(如图2实线)、分段线性逼近策略(如图2虚线)、分段二次多项式逼近策略(如图2点虚线)等.由于计算机采用数字信号,非常符合分段常量策略形式,同时这种策略简便易行、生成参数数目较少.因此本文采用分段常量逼近策略进行控制变量参数化,即采用为基函数.
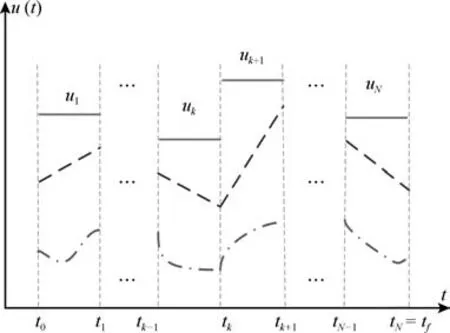
图2 控制变量分段示例Fig.2 Illustration of control variable pro files
从而整个时间段内的控制变量可以表示为:

其中,X[tk−1,tk)(t) 为开关函数,k=1,2,···,N,具体形式如下:

进而每一分段内,控制变量可以表示为:

利用上述中CVP思想对原问题(1)∼(7)进行处理,得到如下有限维动态优化问题,记为P2:
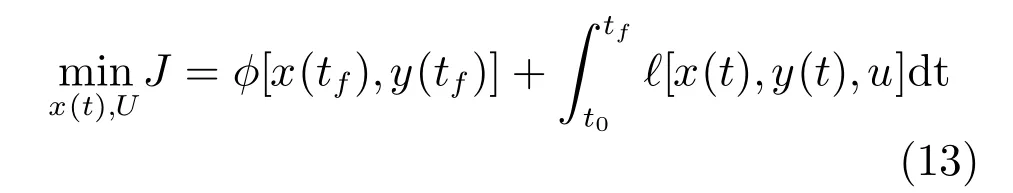
s.t.
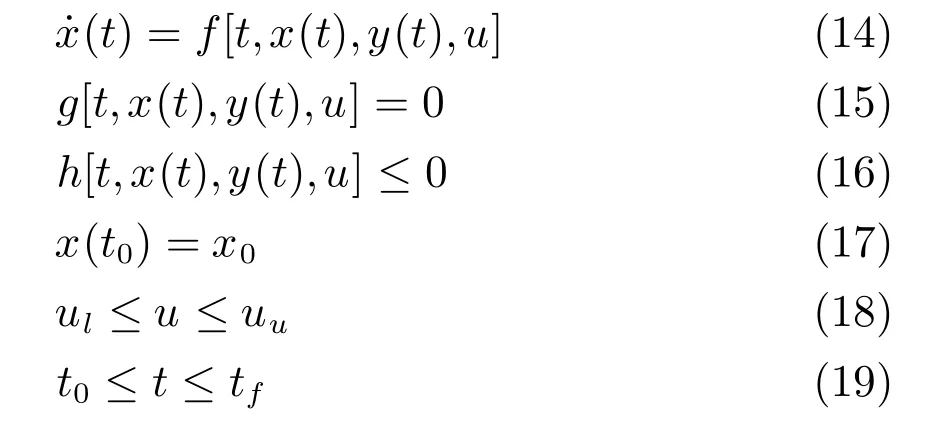
其中,u∈U是v(t)离散化后的有限维控制向量,并且U∈RN是个非空N维向量.其他变量的定义同问题P1.
对于参数化后的DOP问题可使用成熟的基于梯度的优化算法进行求解.本文首先采用BDF直接对微分代数方程组进行求解,进而得到带有有限维控制向量的目标函数,再用BFGS迭代法计算拉格朗日函数的Hessian矩阵的正定拟牛顿近似值,利用SQP算法便可得到最优的控制参数组合.
2.2 不等式路径约束处理
2.2.1 算法步骤
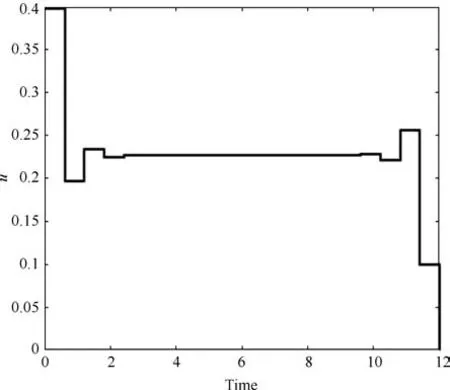
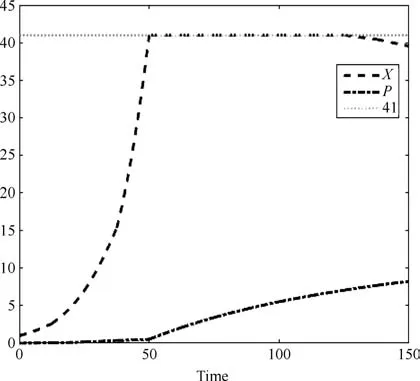
本文利用文献[34]中的分点离散法来处理不等式路径约束,记分段点集合PN={t0,t1,···,tN−1,tN≡tf},ti−1 其中,tj,j=1,2,···,M是时间域内M个违反时间段上的离散形式.给出求解具有不等式路径约束的DAE系统最优控制问题求解具体算法如下: 初始化.设置初始控制参数u(0)、初始化不等式路径约束违反点集合T(0)∗⊂T;有限且任意小的容忍度参数η>0;分段参数N∈N∗;迭代次数p=0;迭代精度δ>0; 步骤1.先解决不带有不等式路径约束的DOP问题P2,i.e.解式(13)∼(15)、式(17)∼(19)构成的动态优化问题; 步骤2.利用BDF法求解式(14),(15)和式(17)构成的DAE初值问题,得到xx(t)的值; 步骤3.在容忍度 下检查h(t)≤η,t∈[t0,tf]的违反情况.将每个CVP分段中违反量最大的点对应的点约束加到DOP的约束中,并且检查已有违反点的违反情况,若不存在违反则去除该点,更新; 步骤4.使用BFGS迭代法计算拉格朗日函数的Hessian矩阵的正定拟牛顿近似值获取关于参数向量的梯度信息; 步骤5.通过SQP方法,求解QP子问题,生成新的迭代步; 步骤6.若在容忍度η下h(ti)≤η,其中,且,则算法结束;否则重新求解带现有点约束的NLP问题,p=p+1,继续步骤2. 若问题P2中的不等式路径约束存在违反,则会循环迭代求解带不同点约束的DOP问题,通过SQP方法调整控制变量u,使得点约束的违反程度有效降低,直至收敛至容忍度η内.不等式路径约束到点约束的转换是收敛的(详细内容参考第2.2.2节),因此通过有限步迭代,能找到满足指定容忍度的KKT最优点. 2.2.2 收敛性证明 在原DOP问题经过CVP处理后的N个控制段上,对于分点离散法的收敛性分析,本文给出以下证明: 对于DAE问题P1的不等式路径约束h(t)=均有以下假设: 假设1.h(t)至少是一阶可导的. 假设2.h(t)对于t是Lipschitz连续的,即存在一个常数K,使得对所有(t)和(),在域D={t0≤t≤tf,|x|≤∞,|u|≤∞}上都有下式成立: 假设3.若h(t)对于t不是Lipschitz连续的,记不连续点集合为Pnon且Pnon∈PM,则h(t)满足假设2,其中tPnon. 定理1.若问题P1的任意一个不等式路径约束h(t)≤0都满足上述假设,则对于该h(t)存在有限的点集使得h(t)≤η:η>0,t∈[t0,tf]. 证明. 原DOP问题经CVP处理后,时间域T∈[t0,tf],i=0,1,···,N−1会被划分为N段相等或者不等的子时间段Ti=[ti,ti+1],i=0,1,···,N−1.在每个子时间段Ti上求解DAE初值问题时,该子时间段将被离散为M个小时间分段,k=0,1,···,M−1,其中=ti,.对于任意一个小时间分段,取由h(t)在上连续,在内可导,那么在内至少存在一点,使等式成立,当时,对等式进一步处理有: 去绝对值进行移项,即 综上,在整个时间域[t0,tf]上的每个子时间段,i=0,1,···,N(η)−1上都有上式成立,因此有 其中,N(η)是η的函数,η是式(22)满足的条件.对于有限的η,N(η)也是有限的. 对于问题P2的每一个不等式路径约束均可此类证明. 本节采用两个DAE系统的最优控制问题对提出的算法进行仿真研究.仿真环境为:Intel i7-4790,3.6GHz CPU和DDMM1/1600 MHZ 8GB内存.在仿真中求解DAE方程组求解精度设为10−6;使用SQP方法解NLP问题,求解精度设为10−4;内点约束的收敛容忍度为η=10−6. 由Guun等提出的催化剂混合问题[39],一直以来被研究者研究用于动态优化问题的研究[40−41].问题可描述为:在长度为lf的管式反应器中,两种物质A、B在管内发生反应.反应式为A↔B→C.其中B是副产物,C是目标产物,反应速率随催化剂沿着管长的混合率而变化.为了得到更多的目标产物C,该动态优化控制问题的求解目标是获得催化剂最佳配比方案.其数学模型如下式所示: s.t. 其中,状态变量x1(l)、x2(l)、x3(l)分别表示为A、B、C的摩尔分率,初始状态为x1(0)=1,x2(0)=0,x3(0)=0;控制变量u(l)表示催化剂沿管长的混合率,满足的约束为0≤u(l)≤1;l在这里表示管长.这里取l0=0,lf=12,仿真中取u0=0.17. 根据本文给出的具有不等式路径约束的DAE系统最优控制问题的求解算法,若不等式在[l0,lf]上存在违反,则将其转化为内点约束x2(li)−0.075≤η.图3和图4是控制变量取为N=24时得到的控制轨迹和状态轨迹.图5为x2(l)的状态轨迹.可以看出在整个长度域l∈[l0,lf]内都满足不等式路径约束,说明本文提出的方法在路径约束处理方面有着很好的效果. 仿真中分别取N=24、29、34,得到问题最优目标函数和求解时间如表1.由表1中可以看出,本文方法求解的时间与文献[18]相比,省时至少20%,精确度方面会因为参数有所浮动,但是目标函数最差在N=29时,本文所得目标函数也已经达到文献[18]的99.97%. 图3 控制曲线Fig.3 Control pro file 图4 路径约束下的状态曲线Fig.4 The status curve with path constraint 图5 路径约束下x2的状态曲线Fig.5 The status curve of x2with path constraint 表1 催化剂混合问题测试结果Table 1 Results of catalyst mixing problem 在文献[42]中描述的一个青霉素分批补料发酵问题(Fed-batch penicillin fermentation),该问题具有很强的非线性和奇异性.该动态优化问题描述如下: 其中,目标函数J是总收益.X是生物量浓度(g/L),P是现有青霉素产物数量(每升活性),具体增长率µ,具体产品形成速率θ和反应堆的体积V(L)都是系统的状态变量.底物浓度S(g/L)是控制变量.进料流量F为1666.67L/h.该模型初始状态为 [X(0),P(0),V(0),µ(0)]=[1,0,250000,0]. 起始时刻[t0,tf]=[0,150].控制变量S∈[0.001,0.5]. 采用文献[18]中处理不等式路径约束的方法与本文方法对比,仿真中取N=12、14、16分别得到最优目标函数和求解时间如表2所示.由表2中可以看出,本文方法求解的时间约为文献[18]的十分之一,精确度方面会因为参数有所浮动,但是目标函数最差在N=12时,本文所得目标函数也已经达到文献[18]的99.3%. 仿真时设置u0=0.5.取控制变量N=12时,图6为得到的控制轨迹,图7是状态轨迹,其中状态变量X(t)≤41.从图中可以看出本文所提方法的有效性. 表2 青霉素分批补料发酵问题测试结果Table 2 Results of fed-batch penicillin fermentation 图6 控制曲线Fig.6 Control pro file 图7 路径约束下的状态曲线Fig.7 The status curve with path constraint 综上两个仿真实验,本文方法允许路径约束违反在用户指定范围之内,在问题允许存在误差或者实际上确实存在误差的情况下,以一定的准确度换取求解速度,满足应用需求. 本文针对带有不等式路径约束的DAE系统的动态优化问题,提出了一种直接求解该类型问题的框架,首先,通过CVP将无限维的动态优化问题转化为有限维的动态优化问题;然后,利用分点离散方法,设计了一个可以在一定容忍度下满足路径约束的算法,并在理论上论证了该算法可以在有限步数的迭代下收敛;最后,利用催化剂混合问题和压力限定批量反应堆问题仿真研究验证了本文所提方法的有效性. 本文对控制变量进行的是等分离散化,但对局部变化较大的控制信号,等分离散化不能准确地反应真实的控制信号.因此本文下一步的工作将研究根据控制信号曲线自适应地进行CVP离散化.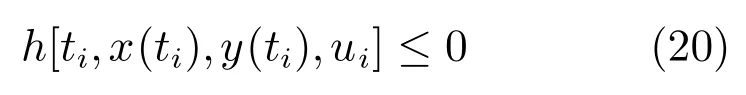
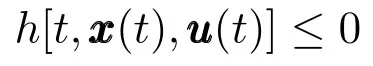


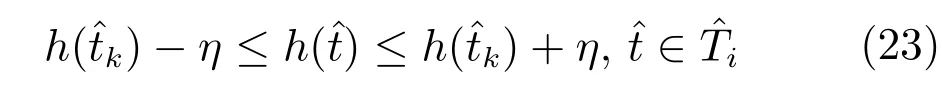
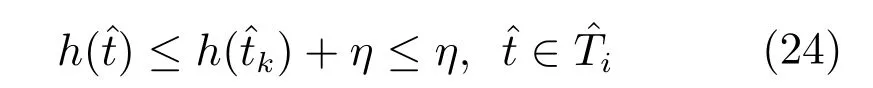
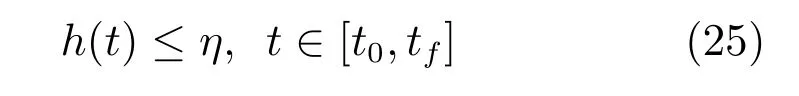
3 仿真研究
3.1 催化剂混合问题
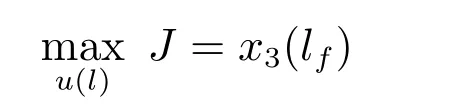
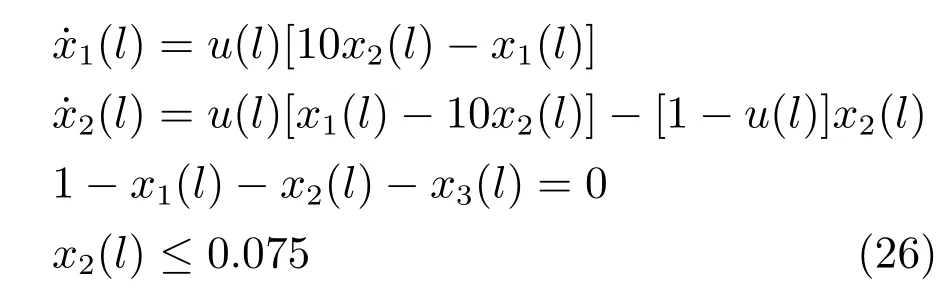

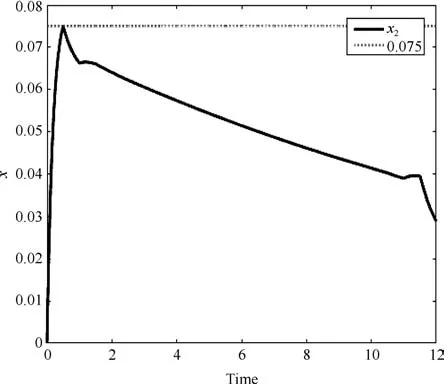
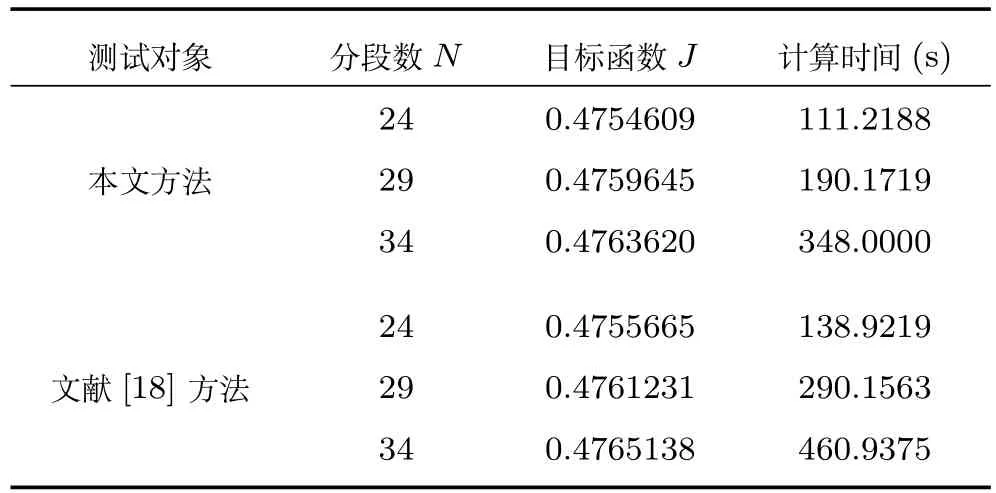
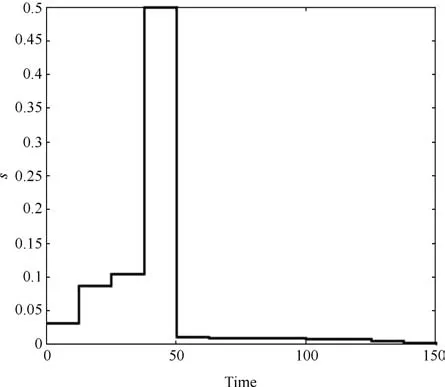
3.2 青霉素分批补料发酵
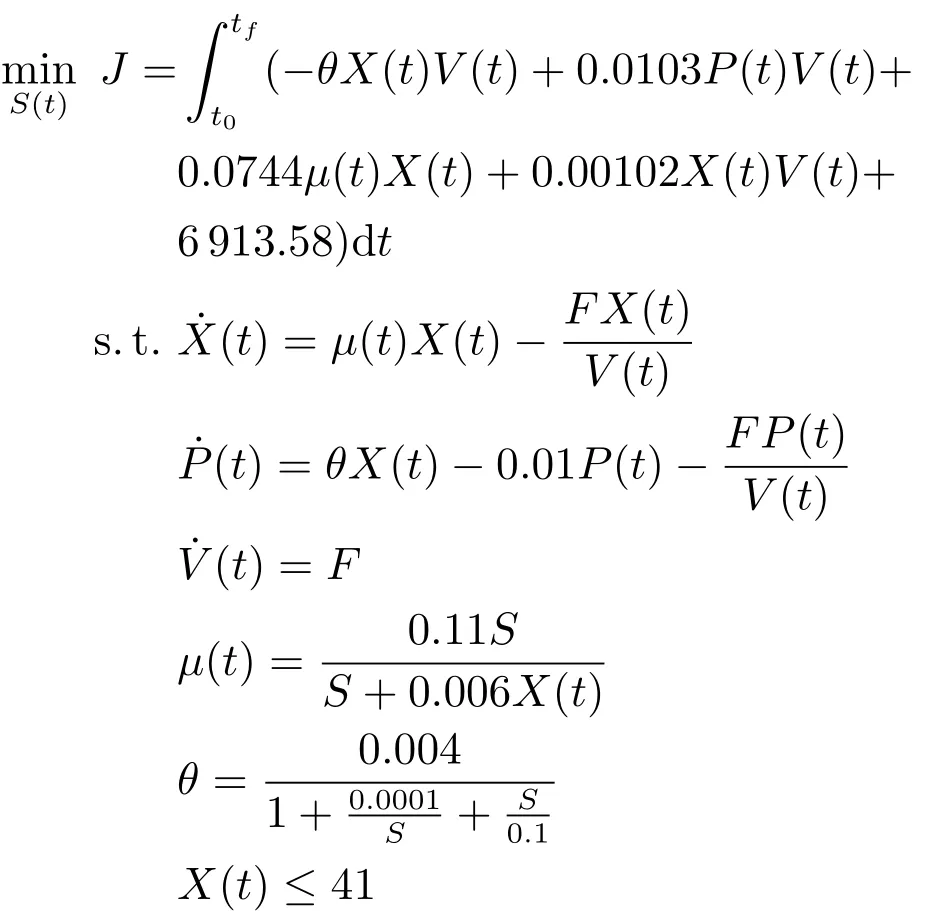

4 结论
