融合纹理信息的SLIC算法在医学图像中的研究
2019-06-11侯向丹李柏岑刘洪普杜佳卓郑梦敬于铁忠
侯向丹 李柏岑 刘洪普 杜佳卓 郑梦敬 于铁忠
超像素算法产生的结果可以大幅提高后续图像处理的运算速度[1],因而被广泛地应用于交互式图像分割[2]、图像去雾[3]、显著性检测[4]、目标跟踪[5−6]、目标分类[7]、3维重建[8]、室内场景理解[9]以及卷积神经网络[10]等领域.
目前超像素算法主要分为两大类:第一类是基于图论(Graph-based)的;第二类是基于聚类(Clustering-based)的.基于图论的超像素分割算法,通过求图的最小割来实现超像素分割.比较有代表性的算法包括归一化割(Normalized cut,NC)[11]、 Superpixel lattices(SL)[12]、 GCa 和GCb[13]、基于熵率的超像素分割(Entropy rate superpixel segmentation,ERS)[14]、SEEDS[15]、Lazy random walk(LRW)[16]、Fuzzy entropy maximization[17−18]、Superpixel hierarchy[19]等.基于聚类的超像素分割方法,是指把多个像素点进行聚类或迭代聚类直到满足特定条件.近些年比较有代表性的包括:TurboPixel[20]、VCells[21]、Simple linear iterative clustering(SLIC)[22]、Simple non-iterative clustering(SNIC)[23]、DBSCAN superpixel segmentation[24]、Linear spectral clustering superpixel(LSC)[25]、Watershed superpixel(SCoW)[26]等,其中SLIC相较于其他算法,由于其简单易懂、速度快、分割结果良好、参数简单等原因,而广受关注.
近年来,有关学者针对SLIC在不同方面的改进包括:无参数化设计[22,27],增加图像预处理[28],改进分割过程[29−31]以及改进融合条件[28]等.
使用无参数化设计,可以减少参数的输入,但是难以保证分割的准确度,尤其是对边缘的贴合程度;增加图像预处理,会使清晰的边缘更清晰,但也会使模糊的边缘更模糊;通过改进融合条件,可以使孤立的超像素块更准确地融合于相邻的超像素块中,但不会对主要分割结果产生影响.
分割过程是SLIC算法的核心部分,对分割结果有着重要影响.Liu等[29−30]的方法,对于色彩变化较大和面积较小的区域分割效果较好,但是对于弱边缘区域的分割效果依然欠佳;南柄飞等[31]的方法融合了纹理特征,但是处理一幅图像平均需要1.4min,并且在欠分割错误率上有着较为明显的不足.
为了更好地提取纹理特征,需要一种更为快速和准确的算法.而LBP算法计算速度快、效果好,同时具有灰度不变性以及旋转不变性等特点[32],所以广泛应用于图像纹理提取上.
在LBP算法的改进中,虽然文献[33−34]提出的方法会增强LBP算法对原图中噪声的鲁棒性,但是其得到的纹理特征均会产生“纹理偏移”以及纹理噪声.针对这些问题,本文提出一种新的LBP算法来提取纹理特征,解决了“纹理偏移”问题并减弱了纹理噪声的影响,然后在SLIC的距离公式中加入纹理距离,使其对于纹理有更好的相应.
在实验中,本文分别选取ERS、SEEDS、LRW、TurboPixel、SLIC、SNIC、LSC 和SCoW 这8种具有代表性的算法进行实验对比.为验证分割效果,本文选取纹理较多的医学图像进行实验,图像数据采用选择了由Alexander Andreopoulos和John K.Tsotsos建立的心脏MRI数据集[35].经实验证明,本算法可以更好地突出不同区域之间的变化,适用于医学图像以及纹理较复杂的图像的分割.
1 基于纹理的SLICT算法
1.1 传统的SLIC算法
SLIC由Achanta等[22]于2010年提出,利用图像颜色相似度和空间距离关系进行迭代聚类.假设在图像中有个N像素点,预计产生K个超像素,则每个超像素的预计边长为,然后在中心点2S×2S的区域内进行k-means迭代聚类,直至达到最大迭代次数.
聚类中计算某点与中心点的距离D的公式如下:
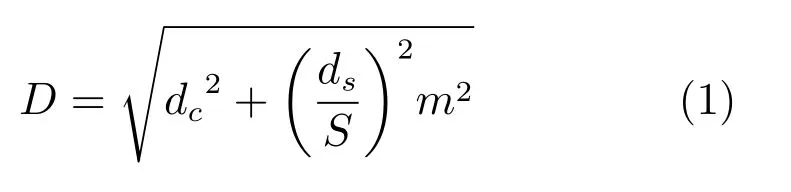
其中
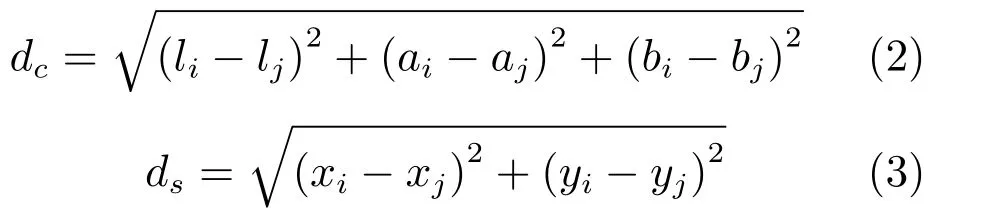
其中,li、ai、bi为点i在Lab色彩空间下的值,xi、yi为点i在图像中的空间位置.m是衡量空间信息和色彩信息的比重,m越小时,则对色彩变化越敏感同时超像素块会越不整齐.一般来说,m取5∼40时会比较有效.此外,对于灰度图像而言,可以使用如下公式代替式(2):
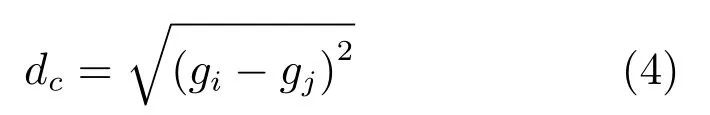
其中,gi与gj分别为点i与点j的灰度值.
1.2 LBP旋转不变统一模式
LBP是一种灰度范围内的纹理度量,由Ojala等[36]提出.设点c是图G不在其上下左右4条边上的某一个点,gc是c的灰度值,p点是在c点P邻域(本文采用的是八邻域)内的一个点,R是P邻域的半径,则该点c的LBP值计算公式如下:
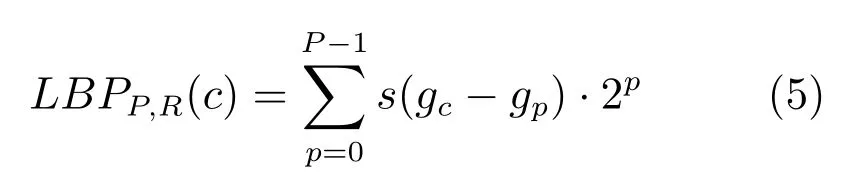
其中
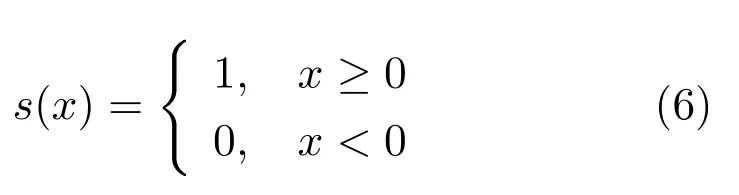
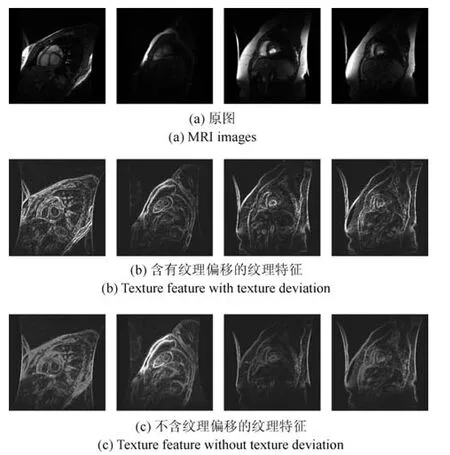
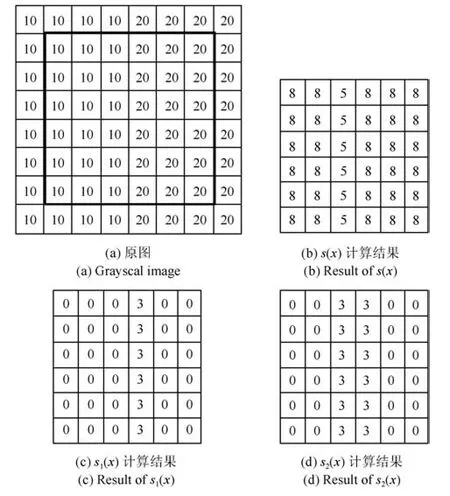
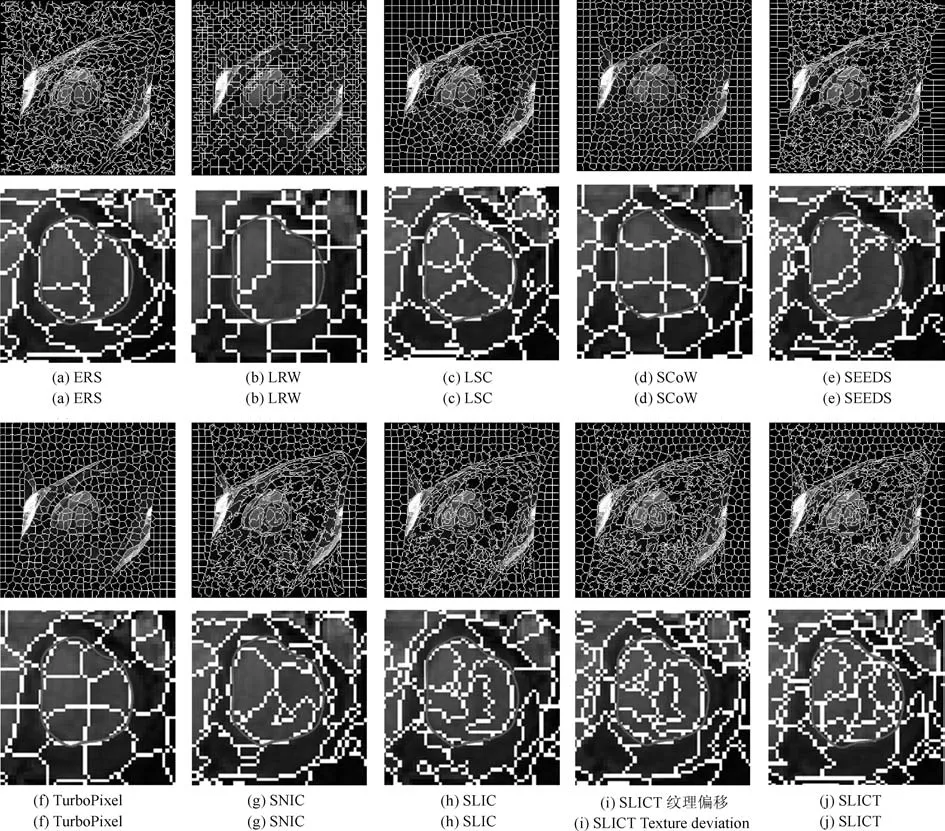
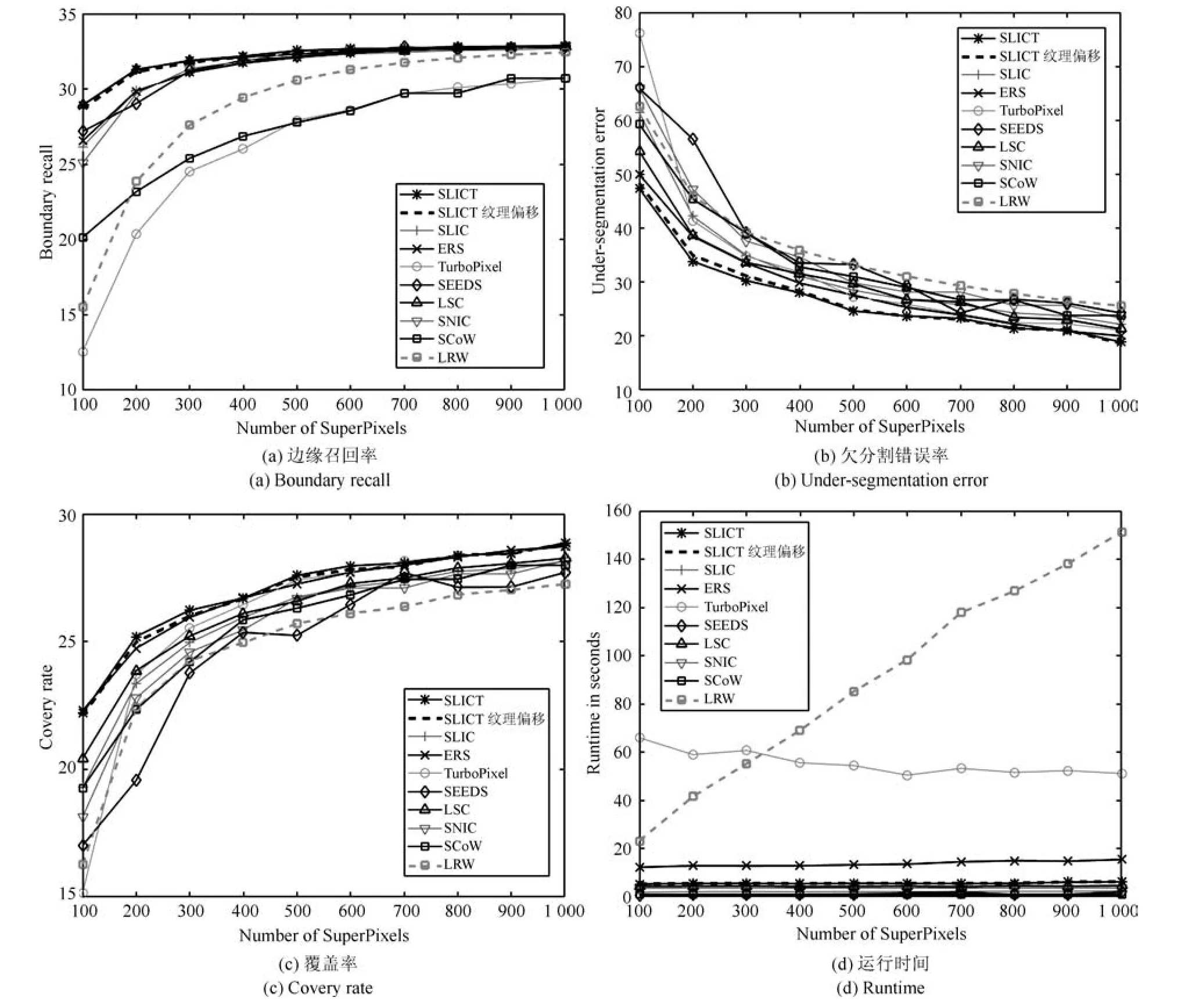
LBP的旋转不变模式[32]是指:不断改变访问中心点P邻域的顺序,得到一组值,取其最小值作为该中心点的LBP值.每个点的旋转不变模式的公式如下:其中,ROR(x,i)为旋转函数,表示将x转化为二进制数后,循环右移i(i 统一模式是指,某点LBP二进制值的跳变(Spatial transaction)小于等于2的模式.该点对应的跳变计算公式如下: 跳变大于2的模式,称为非统一模式(Nonuniform pattern)或混合模式.跳变小于等于2的旋转不变模式称为旋转不变统一模式[37](Rotation invariant uniform pattern,RIU). 为了解决传统的SLIC算法对于纹理不敏感以及传统LBP算法会造成纹理偏移的问题,本文通过改进LBP算法并与SLIC算法结合提出了一种结合无纹理偏移的纹理特征的超像素分割算法—SLICT,该算法的流程如下所示. SLICT算法流程. 输入.1)图像G;2)预分割超像素块数K;3)空间距离权重m以及纹理距离权重L. 输出.与原图同样大小的标号图,同一个标号组成的连通域对应相应位置的超像素块. 步骤1.提取原图对应的纹理特征: 1)求灰度变化方差图,并利用该方差图求每个点对应的thresh(方法见第1.3.1节); 2)利用1)中的thresh计算无纹理偏移的LBP模式(方法见第1.3.2节); 3)利用无纹理偏移的LBP模式计算图G的纹理特征Map(方法见第1.3.3节). 步骤2.初始化聚类中心:将图像分为K个边长为S的规则网格,并将每个格子中心点的横纵坐标、对应位置的Lab颜色以及纹理特征的值作为初始聚类中心,即Ck=[lk,ak,bk,xk,yk,Mapk]T,k=1,2,···,K. 步骤3.调整聚类中心:移动每一个聚类中心至该中心的八邻域内颜色梯度值(见式(9))最小的点. 步骤4.初始化距离和标签:初始化每个点的标签labels(i)=−1,初始化每个点与聚类中心的距离为d(i)=∞. 步骤5.k-means迭代聚类:对于每个聚类中心Ck和其周围的2S×2S邻域内所有的像素点i,计算Ck与i之间的距离D0;如果D0 步骤6.重复步骤5,直到达到最大迭代上限 步骤7.超像素融合:将面积过小的超像素块融入其附近的超像素块之中. 在步骤3中对于不处于图G上下左右4个边上的任意一点c的梯度公式如下,其余值以0补齐: 其中,xc和yc分别是点c的横纵坐标.步骤3中调整聚类中心的目的是为了避免初始聚类中心落在边缘点上,从而影响聚类结果. 在步骤5中的任意两点i、j之间的距离公式如下: 其中 若xi、yi分别是点i的横纵坐标,则Map(xi,yi)=Map(i).dlbp是通过纹理特征计算出的纹理距离,L用于调节纹理距离所占比重,L越大,对于纹理越敏感.实验表明,L的取值为10∼50时效果会比较好. 1.3.1 计算thresh 在文献[33−34]中提到了两种对LBP的改进方法,但是这两种方法并不能很好地处理一些由于光照或是成像等原因引起的纹理噪声.为了减少这些噪声所带来的影响,并突出不同区域之间的差异,可以在计算式(6)中的时加入一个阈值thresh来达到此目的,即: thresh是衡量中心点P邻域内灰度变化强烈程度的数值,所以需要先求得原图对应的灰度变化标准差图,对于不处于图G上下左右4个边上的任意一点c的P邻域内灰度变化标准差为: 其中 则点c对应的thresh计算公式如下: 当thresh=0时,基本等同于传统LBP旋转不变统一模式.此外,这种s(x)计算方法,虽然可以减少纹理噪声但是依然会引起纹理偏移,下文中称使用此s(x)计算的SLICT为SLICT纹理偏移. 1.3.2 计算无纹理偏移的LBP模式 通过式(12)计算出的LBP模式会存在纹理偏移.LBP纹理偏移指的是使用传统LBP计算公式时会使处于边缘两侧的像素点属于不同的LBP模式.这种情况,会使结果所表达的纹理与原图不能完全重合.为了避免这种情况并减少纹理噪声所带来的影响,需要对式(12)中的s1(x)进行如下改进: 则对于不处于图G上下左右4个边上的任意一点c其无纹理偏移的LBP旋转不变统一模式为: 其结果范围为[0,P+1],共计产生P+2类模式,其中第一类到第P+1类分别是在邻域内有多少个点与中心点相比,其灰度值的变化大于thresh,最后一类代表非统一模式. 为进一步说明纹理偏移的影响,使用不同的s(x)公式计算LBP模式图,结果如图1所示. 图1中(a)是一张图像的灰度图,图1(b)∼(d)分别是利用式(6)、(12)、(16)计算出的旋转不变统一模式图,即可以看出图1中(b)与(c)没能很好地覆盖边缘两侧,具体实例分析见第3.2节. 1.3.3 提取纹理特征 使用某模式对应点的P邻域内的灰度变化方差之和来代替某模式包含点的数量,这样可以更好地描述纹理特征[34].但是为了减少明显边缘和弱边缘之间的差别进而突出弱边缘的纹理特征,本文使用某模式对应点的P邻域内的灰度变化标准差之和来代替某模式包含点的数量.其中某点c的P邻域内的灰度变化标准差varP,R(c)的计算方法见式(13). 而varP,R(c)对于图像噪声、颜色变化过大的边缘区域或纹理复杂区域的浮动过大,从而造成在计算LBP各模式的比例时(式(19))容易出现比例失衡的情况,所以为进一步突出弱边缘的纹理特征,对varP,R(c)进行极值抑制.方法是:使用最大类间方差法[38]找到合适的阈值Press把varP,R(c)分成两类,将大于Press的部分置为Press,其公式为: 图1 LBP算法中有无纹理偏移的效果对比Fig.1 The results of LBP algorithm with and without texture deviation 然后利用所有像素点的varP,R0值,计算各模式所占的比例LBPWeight(k),即: 其中 其中,sum(·)表示计算集合内所有元素的个数,k代表模式的种类. 之后对LBPWeight(k)进行归一化,即: 则对于不处于图G上下左右4个边上的任意一点c,其对应的纹理特征Map(c)为: 其余的点对应的纹理特征值以0补齐. 1.3.4 进行图像分割 按照SLICT算法流程中步骤5和步骤6的步骤进行迭代聚类,然后使用文献[22]中的方法,消除面积过小的超像素块,得到最终的分割结果.此外,以上流程是针对灰度图像而言.如果需要分割图像是彩色图像,需要将其转化为灰度图像,并利用此图像计算dlbp. 为了验证SLICT的有效性,本文采用了边缘召回率、欠分割错误率、覆盖率以及运行时间这4种评价指标进行验证,其中前三项的定义和计算方法分别是: 1)边缘召回率(Boundary recall) 边缘召回率描述超像素边缘与人工标记边缘的贴合程度,值越大说明贴合度越好.定义是:人工标记边缘中位于超像素边缘至多两个像素距离内的部分占总标记边缘的比例. 2)欠分割错误率(Under-segmentation) 欠分割错误率是一个从超像素块外部来衡量分割效果的指标,表示人工标记区域所在的所有超像素块有多少“溢出”了人工标记的范围.设共分割出K个超像素块,某个超像素块为sj,人工分割区域为M,|·|表示该区域的面积,α为欠分割错误率参数,其取值一般为sj面积的5%,则其公式计算如下: 3)覆盖率(Coverage rate) 覆盖率是在只有一个人工标记区域的情况下,最大可达分割率(Achievable segmentation accuracy)[30]的简化计算方法,值越大,则说明对人工标记区域的分割越完整.计算公式如下: 为了更好地验证本算法的有效性和时效性,将SLICT、SLICT纹理偏移以及上文提到的8种超像素算法应用于纹理较为复杂的医学图像之中,分析各自的运行效果,并在这部分详细分析纹理偏移现象对分割结果和所求纹理特征的影响. 由于医学图像中存在着多种不同类型的纹理且各种纹理比较复杂,所以为了更好地验证本算法的准确性和鲁棒性,将上述的10种算法应用于医学图像中的心脏MRI图像上,其部分结果如图2所示. 图2中第1行和第3行是本文提出的SLICT算法以及其他超像素算法应用于7980张MRI数据库中的部分实验结果截图,第2行和第4行分别是第1行和第3行心脏区域的放大结果.这部分使用的实验参数为m=5,L=30,预计分割超像素块数为600.可以看到,SLICT对于边缘以及弱边缘(如心脏上的较暗区域的边缘和图像两侧灰度值为0的区域的边缘)的响应是最好的,其次是SLIC、SLICT纹理偏移、SEEDS、SNIC以及LSC. 在规整度上,TurboPixel以及LSC的图像是最规整的;ERS最零乱,即使对于灰度值为零的图像左右两侧区域,生成的超像素块依然很零乱;此外为保证LRW 的时效性,在进行超像素分割时将图像缩小至原图像的1/4,故而其分割结果在原图上呈现时显得较为整齐,但是其超像素块在纹理较少的区域分布并不均匀.从实验结果上看,基于图论的算法ERS、LRW 与SEEDS产生的超像素块结果均不整齐,而其余基于聚类的超像素算法产生的超像素块则普遍整齐很多. 为进一步验证算法的优劣,在图3中给出了各算法在心脏MRI数据库中有人工标记的5011幅图像上的运行结果,并计算和记录了上述提到的4种评价指标. 从图3中可以看出,本文提出的方法的分割效果在总体上优于其余算法.在边缘召回率上,SLICT与LSC相差不多,略优于SLICT纹理偏移;而这三种算法均明显优于其余算法;TurboPixel因为其分割结果更倾向于贴合种子节点附近的网格而非贴合目标区域边缘,所以有着较为明显的不足;除却SCoW、TurboPixel以及LRW以外的7种算法对应的边缘召回率,在预计分割数量达到1000时,几乎都达到了99%以上.此外,因为图像本身分辨率较低,而且人工标记区域面积较小,所以此值会比常用的自然光数据库(如BSDS500)上要大一些;由于同样的原因,在欠分割错误率上,结果也会大一些. 图2 心脏MRI分割结果Fig.2 The results of superpixel algorithms on MRI images 在欠分割错误率上,SLICT效果最好,优于SLICT纹理偏移,其次是ERS与LSC;而LRW与SEEDS在此表现相对较弱.因为ERS所分割出的超像素块不规则以及对于纹理较少的区域灵敏度较差,造成在人工标记区域周围的超像素块面积较小,所以其在此方面表现稍好.同时在实验中发现,由于人体器官形状以及MRI成像原理的复杂性,人工标记区域往往会比较贴合器官的实际形状而非图像上表现出的形状,所以在欠分割错误率上,以上所有算法在不同图像上均表现出较大的波动. 在覆盖率上,SLICT优于SLICT纹理偏移,而ERS在边缘区域会分割出更多小块的超像素,但是对于纹理的相应程度仍不及本文提出的算法,位列第三;值得注意的是,SEEDS算法在这一点上表现出了较大的波动.其他8种算法只考虑了色彩以及空间信息,而且MRI图像会有弱边缘以及模糊区域,从而造成对弱边缘区域不敏感,在最终的分割结果表现上,则是将更多边缘不明显的心脏区域与部分心包膜分在一个超像素块中. 在运行时间上,SLIC、SLICT、SNIC、SEEDS、LSC、SCoW 与TurboPixel的时间复杂度均为O(N)[15,20,22−23,25−26],而ERS的平均时间复杂度为O(NlogN),最大时间复杂度为O(N2logN)[14],LRW的时间复杂度为O(itr·N2),其中itr代表最大迭代次数[16].从结果上看,速度最快的是SCoW与SEEDS,平均处理一幅图像不到0.05s;SLICT平均处理一幅图像需要0.15∼0.2s左右,能够满足实际需求;TurboPixel的运行时间明显慢于同数量级的其他方法,这一点与文献[22]中的描述匹配;LRW的运行时间会随着超像素块数的增多而出现线性的增长,这一点很难满足实际的需求. 图3 心脏MRI数据库运行结果Fig.3 Expriment data on MRI dataset 为进一步说明纹理偏移在提取纹理特征上的影响,在图4(b)和(c)中分别展示了使用s1(x)与s2(x)的结果图,其中某点c的颜色越亮,表示该点的纹理特征的值(即Map(c))越大. 可以看出,后者纹理噪声较少,边缘更加完整连续平滑,不同区域间的对比更大,相同区域间的连续性更强、变化性更小,对于弱边缘和纹理的表达更加清晰.这一点也可以从具体的数据上看出来,由于式(12)对纹理的描述存在偏移,整体上弱于SLICT;但是偏移量只有一个像素,所以在整体上也优于其余算法. 本文通过改进传统LBP旋转不变模式的计算方法,来提取图像对应的纹理特征,并将其与SLIC算法融合,提出了一种对于纹理更加敏感的超像素分割算法—SLICT.将SLICT应用于心脏MRI数据库中的图像,其结果表明SLICT具有更好的准确性以及鲁棒性,对弱边缘以及细小的纹理有着更为优秀地响应.从数据上看,SLICT在欠分割错误率以及覆盖率上优于其余算法,在边缘召回率上与LSC并列第一,在运行时间上平均只需要0.15s∼0.2s,可以满足图像分割和处理的需求.同时验证了使用传统的LBP计算纹理特征时会导致“纹理偏移”,使得其求得的纹理特征不能很好地描述边缘并且存在一定的纹理噪声,从而影响分割结果. 此外,在实验中发现,医学图像中器官存在的弱边缘和模糊区域,会导致呈现出的形状与实际形状有着一定差异.本文提出的SLICT可以很好地检测出这些差异部分,并能够产生更为准确的分割结果,对后续医学图像处理的相关研究有着重要的参考价值和影响. 图4 纹理特征图Fig.4 Texutre feature
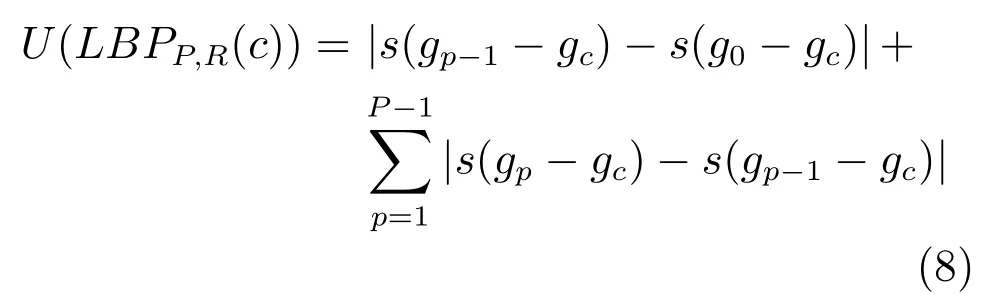
1.3 SLICT算法流程
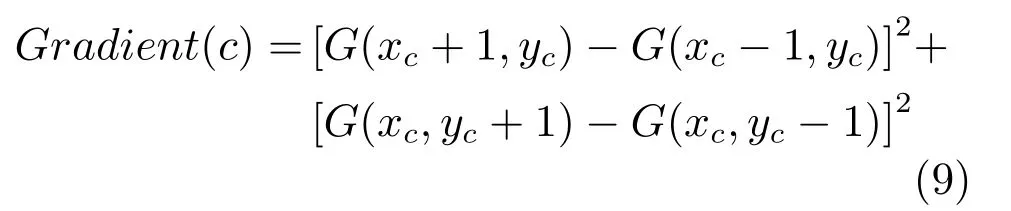
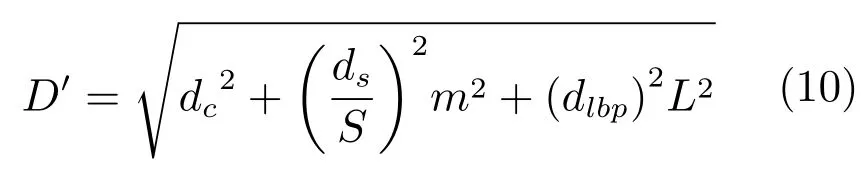

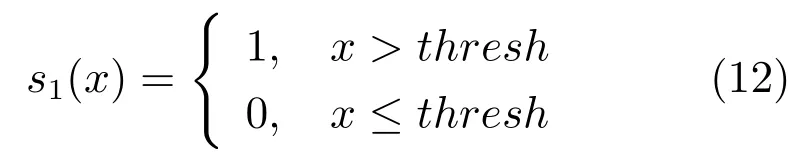
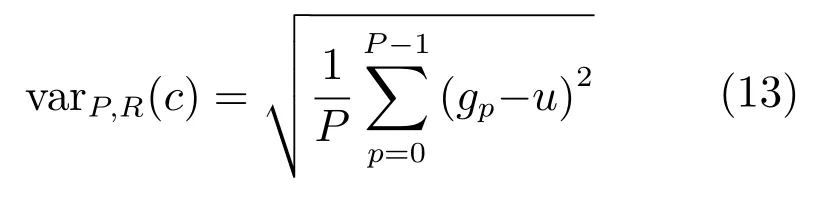
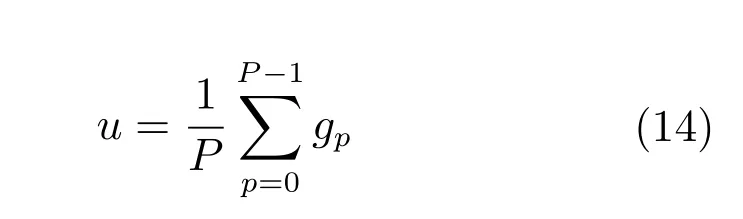
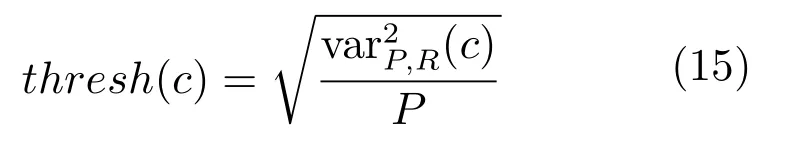
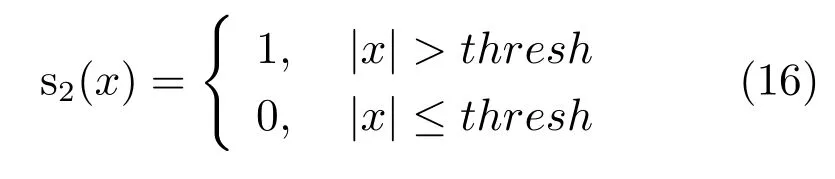


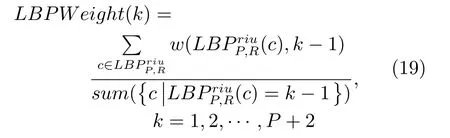

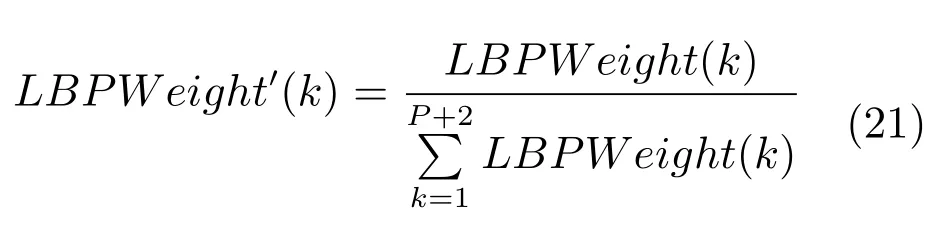
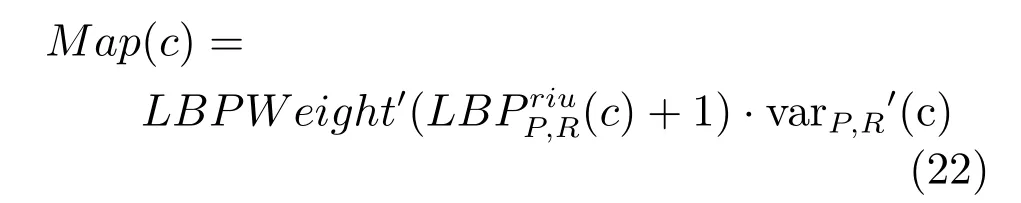
2 评价指标
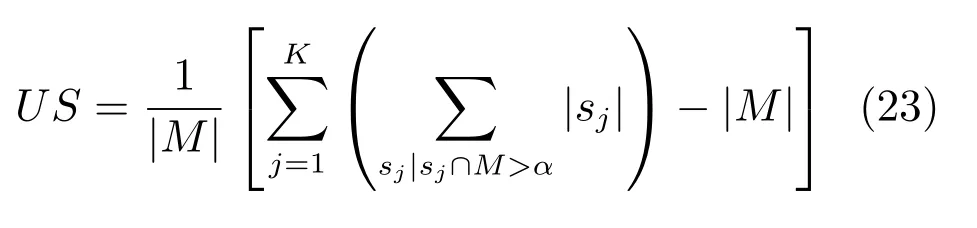
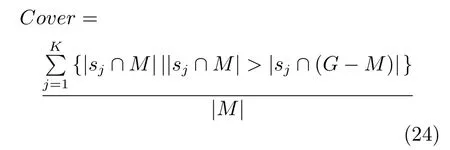
3 实验结果分析
3.1 SLICT在医学图像中实验及结果分析
3.2 纹理偏移影响分析
4 总结