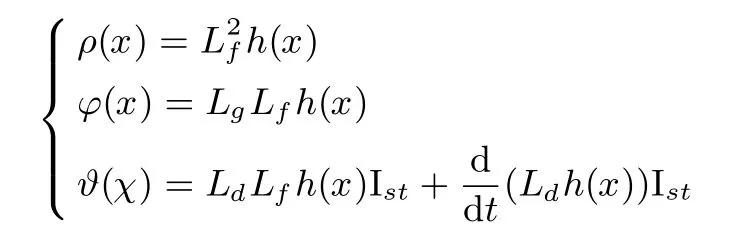PEMFC空气供给系统的二型自适应模糊建模与过氧比控制
2019-06-11王永富马冰心柴天佑张晓宇
王永富 马冰心 柴天佑 张晓宇
为了解决能源危机和全球变暖问题,当前世界各国都在加大新能源开发力度.质子交换膜燃料电池(Proton exchange membrane fuel cell,PEMFC)是一种通过电化学反应将储存在燃料中的化学能直接转换为电能的电化学装置,具有高功率、高能量转换效率、低温启动、无环境污染等优点,应用前景广阔、已逐渐在新能源汽车和电力系统等领域得到实际应用[1−4].
合理控制PEMFC空气供给系统阴极注入空气流量与电化学反应消耗空气流量之比,即过氧比(Oxygen excess ratio,OER)是提高PEMFC系统输出净功率的有效方法.为此,国内外学者对PEMFC空气供给系统的建模与控制问题作了大量研究.文献[5−7]基于以下理想假设建立了PEMFC空气供给系统的基础数学模型:1)视空气为理想气体,遵循理想气体定律,且干燥空气中21%为氧气成分,79%为氮气成分;2)空压机机械效率较高,摩擦力矩忽略不计;3)冷却器体积忽略不计,并可迅速降低空气温度到80◦C;4)排出阴极的空气特性与阴极内空气特性相同;5)阴极内水蒸气平衡得到很好地控制,且无液态水存在.基于以上基础模型及改进模型,国内外学者提出采用线性反馈控制、模型预测控制和滑模控制等方法对PEMFC空气供给系统进行了控制研究[8−12].但以上文献控制器的设计均是基于理想模型,且在模型结构、参数或者模型函数界严格已知条件下进行的,目前如何有效辨识PEMFC模型结构、参数和函数界仍是一困难问题.实践表明,模糊逻辑系统和自适应控制技术相结合是解决复杂而无法建立精确数学模型系统的控制问题的有效途径之一.但模糊逻辑系统和自适应控制技术在处理PEMFC空气供给控制系统中不确定性和不精确性问题的研究很少,特别是采用二型模糊逻辑系统、自适应技术并结合Lyapunov稳定性分析开展研究的鲜有报道.
自从Zadeh教授提出I型模糊集合(T1-fuzzy set,T1-FS)理论以来,基于T1-FS的I型模糊逻辑系统(T1-fuzzy logic system,T1-FLS)成为处理不确定性、模糊性和不精确性建模问题的有效方法,并在众多领域得到了广泛应用.随着理论和实际应用的发展,人们逐步意识到一型模糊集合在描述多重模糊不确定性方面的局限性,使得一些从事一型模糊集合研究的学者们开始转而研究二型模糊集合.特别是近年来二型模糊集合和二型模糊系统的理论与应用得到了快速发展.这是因为一型模糊系统采用了由精确隶属度函数表示模糊集合,其直接处理模糊规则不确定性的能力非常有限,而二型模糊集合和二型模糊系统能较好地解决这些不确定性问题[13−17].虽然该领域在Mendel教授的推动下得到了快速发展,但在许多原创性问题上还在被探索研究,如最近两年我国学者王立新教授探索了二型模糊集合和二型模糊逻辑系统的新框架[18]、王飞跃和莫红教授探索了二型模糊集合的一系列新定义[19].这些新框架新定义与Mendel定义的流行框架哪个更好,或者说针对不同应用对象哪个定义更匹配、目前没有准确对比报道还需进一步研究.
模糊系统和自适应控制的结合是对非线性不确定系统进行建模与控制的一种有效方法,自适应模糊建模与控制的基本出发点是仿人的智能以实现对复杂不确定性系统进行有效的建模与控制,它具有从环境自学习、适应环境的能力.该方法不需要对象模型结构和参数完全已知的条件,仅根据被控系统结构关系即可实现有效控制,已在许多领域的建模和控制中得到广泛关注[20−25].目前,解决PEMFC空气供给系统的控制问题,一般都是首先建立空气供给系统的机理模型、然后进行控制器设计.而进行智能建模和控制方面的研究工作较少.
本文对PEMFC空气供给系统的模糊建模与过氧比自适应控制问题做了一些探索研究、主要工作如下:1)本文首先对国际文献中的一些推导错误及多漏写失误进行了改正,从而保证仿真状态空间模型的正确性;2)为了设计非模型的自适应模糊控制器,采用精确线性化技术求解了系统相对阶数;3)基于等价模型,对PEMFC空气供给系统模型中的多个未建模动态采用二型模糊系统建模,这种方法对PEMFC空气供给系统进行建模在国内外很少有报道;4)结合具体的PEMFC空气供给系统的建模与控制问题,从Lyapunov稳定性导出自适应律并设计了相应自适应控制器.这种结合二型模糊系统建模、自适应控制和稳定性分析,在国际主要文献上未见.大部分PEMFC系统文献局限在简单的模糊控制、或者有自适应功能但缺少稳定性分析等;5)仿真及其对比实验验证了该控制器的有效性与实用性.
1 PEMFC空气供给系统的数学模型
PEMFC系统主要由氢气供给系统、空气供给系统和反应电堆三部分构成(见图1),其中PEMFC空气供给系统包括空压机、供应管道、冷却器、加湿器、电堆阴极以及回流管道等组成.PEMFC空气供给系统具体结构如图1虚框所示.
1.1 PEMFC空气供给系统的建模
为了实现PEMFC空气供给系统的高级控制方法的研究.文献[5]在理想假设基础上,基于文献[7]的流体力学、热力学和电化学等基础物理方程建立了含6个状态变量的PEMFC空气供给系统的非线性状态空间模型,即:
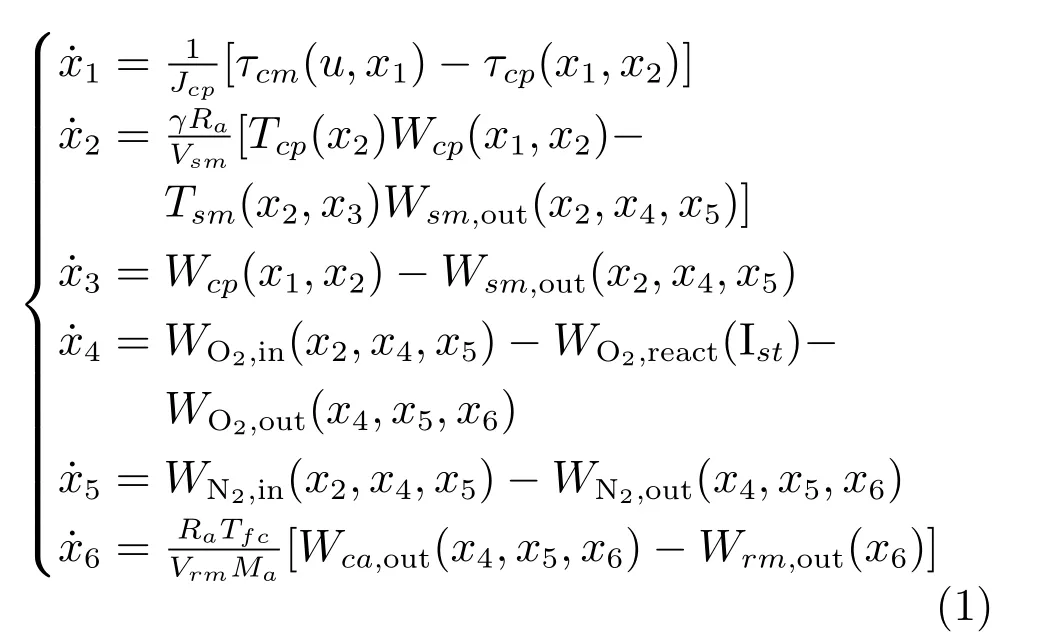
其中,Jcp为空压机转动惯量,u为空压机工作电压,τcm为空压机驱动力矩,τcp为空压机负载力矩,γ为空气比热容比,Ra为空气气体常数,Vsm为供给管道体积,Tcp为空压机流出空气温度,Wcp为空压机流出空气流量,Tsm为供给管道流出空气温度,Wsm,out为供给管道流出空气流量,WO2,in为阴极注入氧气流量,WO2,react(Ist)为电堆反应消耗氧气流量,Ist为负载电流,WO2,out为阴极流出氧气流量,WN2,in为阴极注入氮气流量,WN2,out为阴极流出氮气流量,Tfc为电堆温度,Vrm为回流管道体积,Wca,out为阴极流出空气流量,Wrm,out为回流管道流出空气流量,Ma为空气摩尔质量.
注1.该模型中存在多处推导失误公式、参数及误打的错误需要修正,详细修正内容见本文附录A.
基于方程组(1)和附录A的修正后,PEMFC空气供给系统可表示为如下状态空间方程:

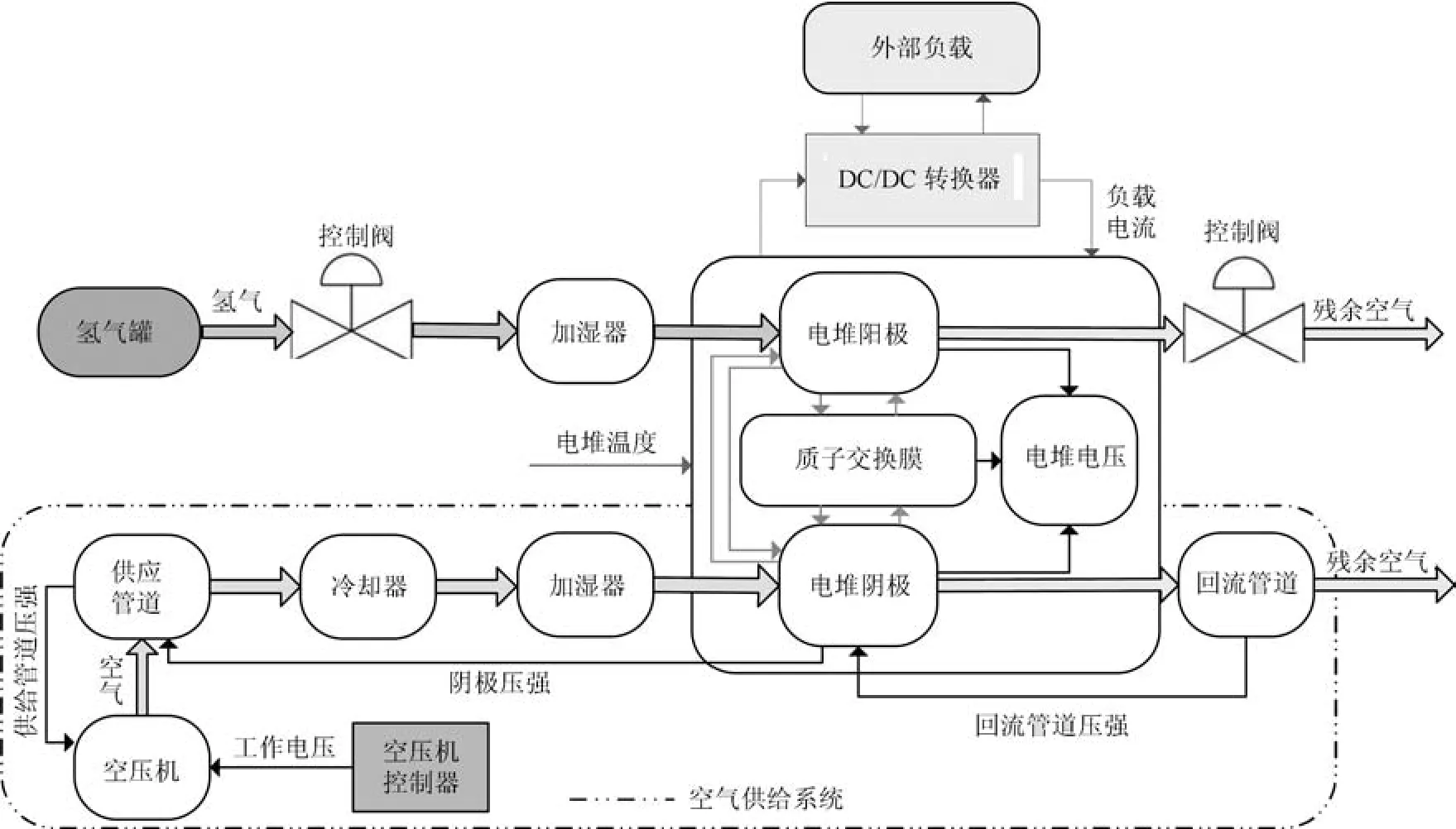
图1 PEMFC模型结构示意图Fig.1 Structure diagram of PEMFC model
其中,x表示该系统的状态向量、其含义如表1所示,PEMFC系统负载电流Ist视为外界干扰,f(x)、g和d分别为:

其中,ηcm为空压机电机的机械效率,Kt、Rcm为空压机电机参数,n为单体电池个数,MO2为氧气摩尔质量,F为法拉第常数.f1(x1,x2)−f6(x4,x5,x6)函数的具体表达式见附录B.
根据近年来国内外研究可知,PEMFC系统负载电流一定时,当系统过氧比λO2达到理想过氧比λO2,ref时,系统输出净功率为最大值(见图2).因此,选择系统输出方程为:PEMFC系统理想过氧比λO2,ref可表示为[8]:
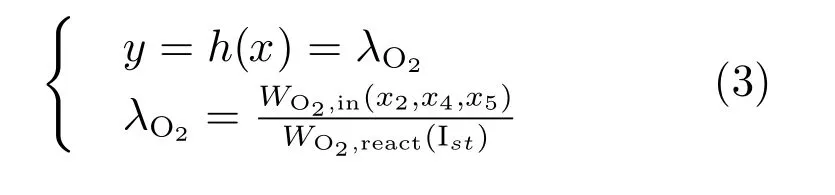

表1 PEMFC空气供给系统状态变量Table 1 State variables of PEMFC air supply system

图2 PEMFC系统负载电流、过氧比和输出净功率的关系Fig.2 Power relationship of PEMFC system load current,OER,and output net

结合式(2)和式(3),PEMFC空气供给系统状态空间表达式可表示为:
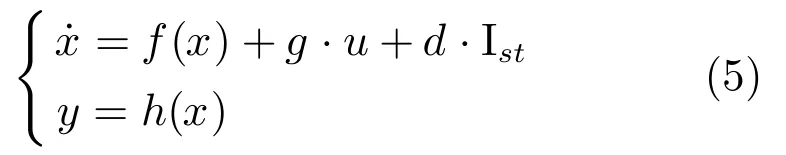
1.2 PEMFC空气供给系统的精确线性化
本文通过非线性状态和反馈变换,对式(5)的非线性状态实现精确线性化,输出方程李导数Lfh(x)、Lgh(x)和Ldh(x)可表示为:

由于Lgh(x)= 0,对系统继续求解李导数.、LgLfh(x)和LdLfh(x)分别表示为:
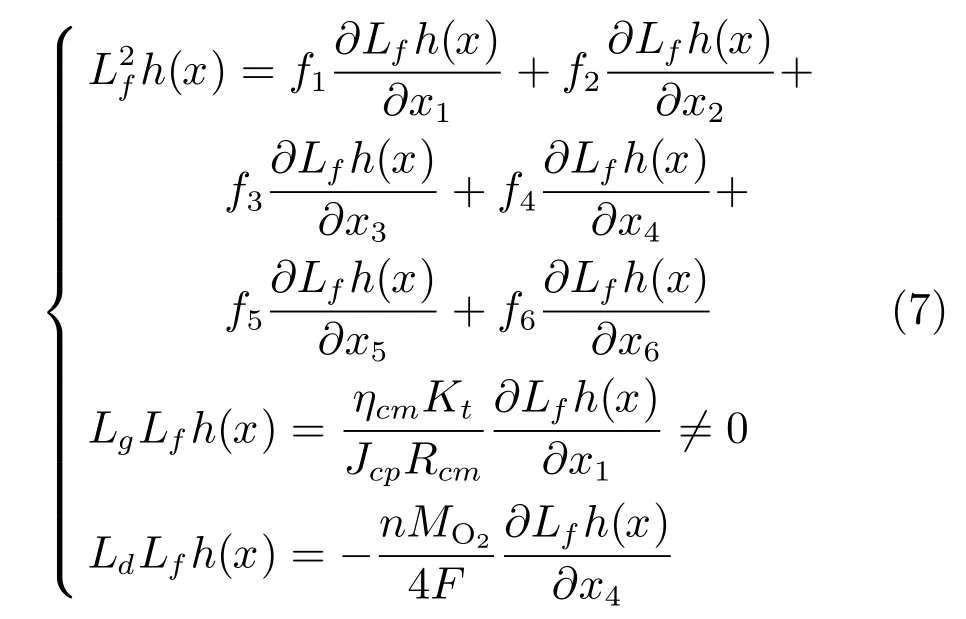
由上可知PEMFC空气供给系统相对阶数为2,小于表达式(5)所描述的系统阶数,方程(5)可转化成以下等价系统:

对于系统(8),如果ρ(x)、ϕ(x)和ϑ(χ)结构和参数完全已知,则理想控制律为:
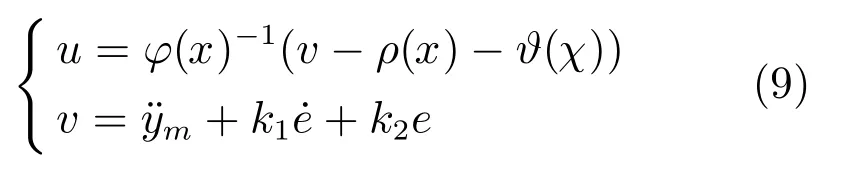
其中,e=ym−y.然而在ρ(x)、ϕ(x)和ϑ(χ)未知情况下,获得理想控制器(9)是不可能的.在这种情况下,本文设计下面II型模糊逻辑系统分别逼近未建模动态ρ(x)、ϕ(x)和ϑ(χ).
2 II型模糊逻辑系统
只要在模糊规则前件或后件隶属度函数中包含二型模糊集(T2-FS),相应的模糊系统即称为二型模糊逻辑系统(T2-FLS).本文模糊规则前件采用二型模糊集(T2-FS),而后件由于采用自适应调节、选用一型模糊集(T1-FS),该二型模糊系统的降型采用Karnik和Mendel提出的方法(国际上简称KM算法[26]).由于本文所采用的二型模糊系统后件是一型自适应模糊集(T1-FS),故在二型模糊系统的降型处理时仅调用一次KM算法、从而提高了算法在线实时计算效率.
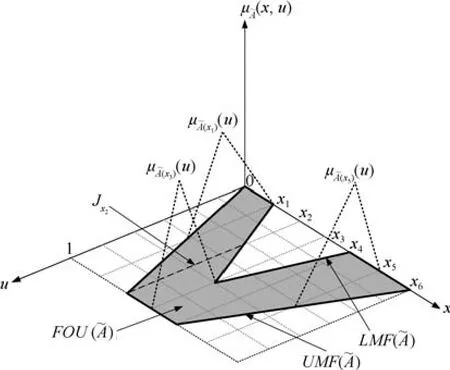
图3 二型模糊集合的各元素Fig.3 Various elements of type-2 fuzzy set
定义1[27−29].一个二型模糊集合(见图3)可以表示为一个二型隶属函数(x,u),其中,x∈X,u∈Jx⊆[0,1],即:
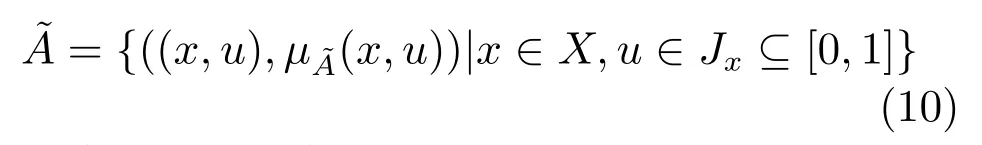
也可表示下面形式:
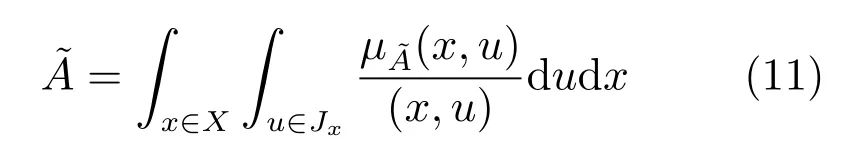
其中,x为主变量,u为次变量,Jx⊆[0,1]为主隶属度,为次隶属度,表示所有可允许x与u之并.由于本文采用的是区间二型模糊集,取.针对上面二型模糊集合的定义,其不确定覆盖域(Footprint of uncertainty,FOU)定义如下:
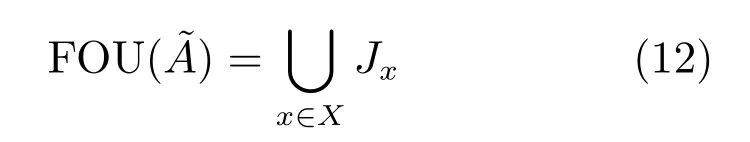
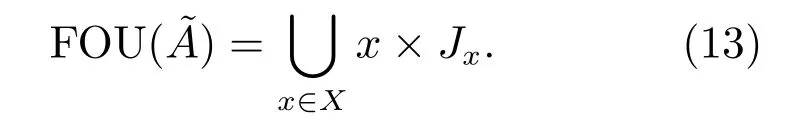
注2.上面Mendel对二型模糊集合和不确定覆盖域的定义,被国外绝大部分文献采用.但我国学者莫红和王飞跃教授认为此定义有欠缺,对二型模糊集合和不确定覆盖域(FOU)进行了新定义.文献[30]认为一个二型模糊集合的不确定覆盖域(FOU)为论域上每一点与在该点的主隶属度的笛卡尔积之并,也就是:如果从数学角度看,式(13)比式(12)更严谨.假设按照式(12)计算FOU,结果可能是一个区间,而非Mendel所想表达的图3阴影面积.造成这种的原因可能是Mendel先预设定了不确定覆盖域(FOU),然后用符号表示累加移动的意思,而非传统意义上的并运算.本文不确定覆盖域(FOU)的计算按照式(13),或者用式(12)计算、但符号表示累加移动的意思.
在上面二型模糊集合定义后,考虑n输入单输出的Mamdani区间二型模糊逻辑系统,其中输入xi∈Xi,输出y∈Y,i=1,···,n.假设 IT2-FLS中包含如下M条模糊规则:

步骤1.对于某条规则,计算输入向量x的激活区间:
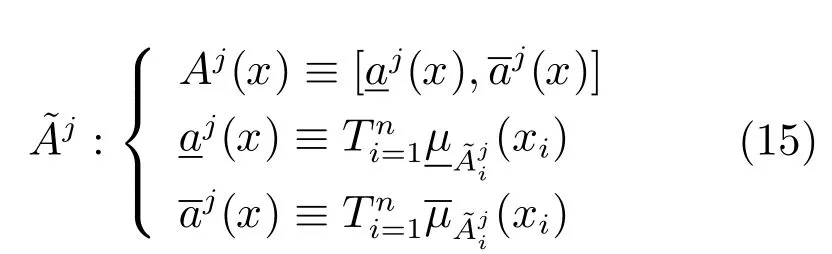
步骤2.对于某条规则,输出变量y的最大隶属度所对应的值为:

步骤3.在前件的激活区间和后件的输出Θj计算后,基于KM算法的降型可表示如下:
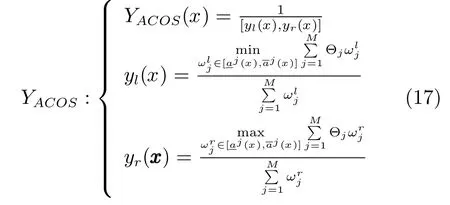
其中,[yl,yr]为用KM算法得到的输出区间.
步骤4.加权平均反模糊化后,可将上面的IT2-FLS简化成下面基函数的形式:
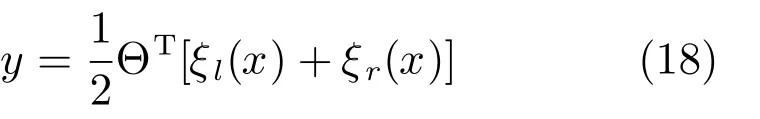
其中, Θ = [Θ1,···,ΘM]T为二型模糊系统的自适应参数向量,二型模糊系统的左基函数为二型模糊系统的右基函数为
3 自适应控制器设计
对于系统(8),在ρ(x)、ϕ(x)和ϑ(χ)未知情况下,用前文式(18)分别对ρ(x)、ϕ(x)和ϑ(χ)进行在线逼近,新的控制器为:

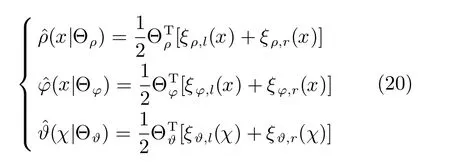
定义本文二型模糊逻辑系统最优参数向量Θ∗和对应的逼近误差ω分别为:

应用式(19)到式(8)并结合上面的定义,经过几步直接的运算后,可得如下的跟踪误差方程:
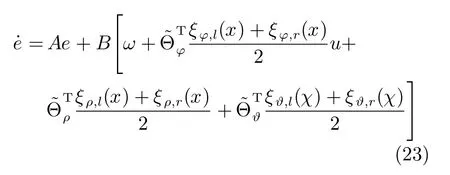
定理1.对于系统(8)在状态变量和负载电流可测的条件下,相应的控制器为式(19),Θρ、Θϕ和Θϑ的自适应律为式(24)∼(26):
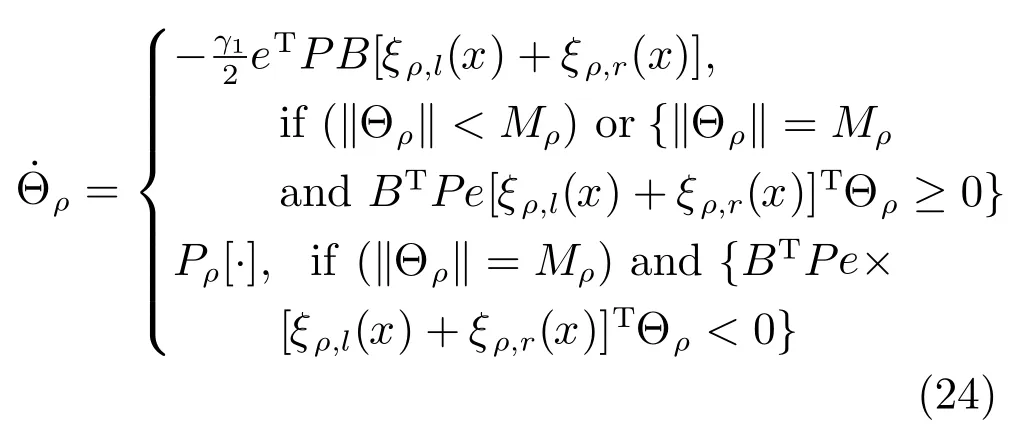
其中,投影算子Pρ[·]可表示为:

其中,投影算子Pϕ[·]可表示为:
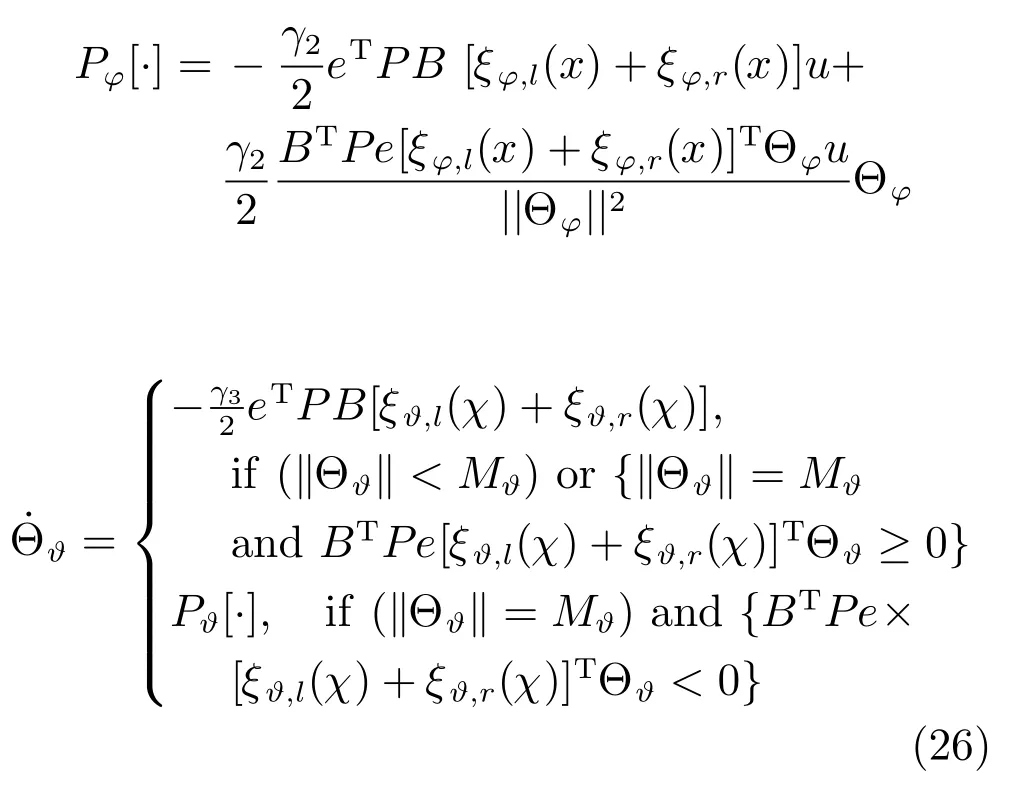
其中,投影算子Pϑ[·]可表示为:
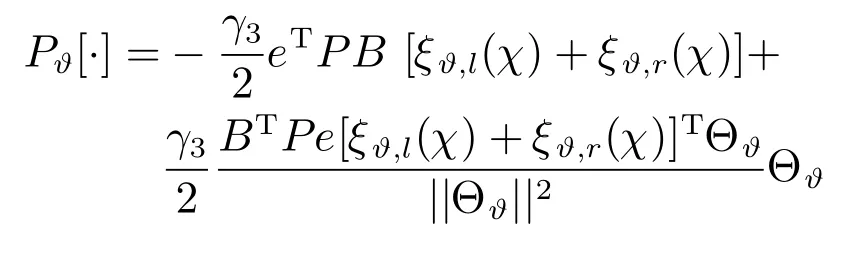
其中,γ1、γ2和γ3为正常数,Mρ、Mϕ和Mϑ为系统约束集,P=PT为满足下面的Lyapunov方程:
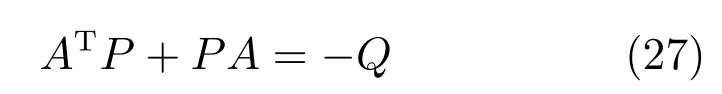
那么跟踪误差e是一致最终有界的.
证明.取Lyapunov函数为:
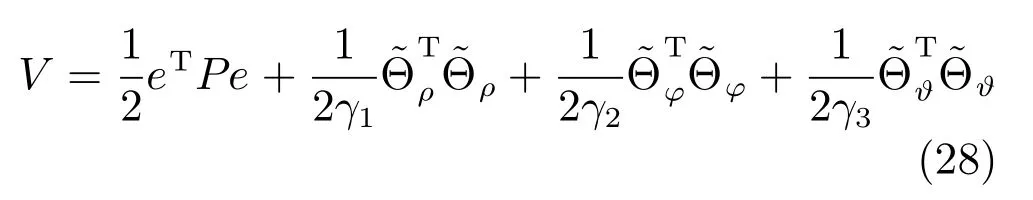
其中,P=PT.微分(28)可推出:
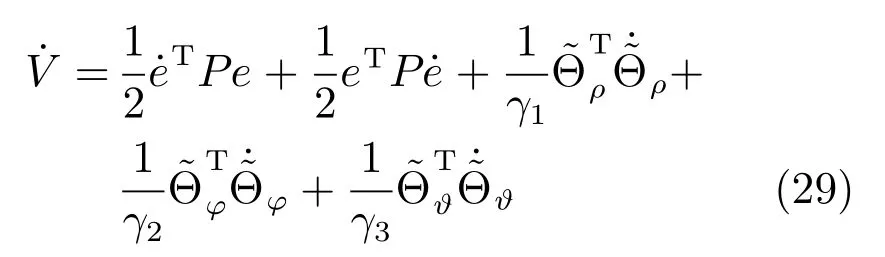
基于式(23)和式(27),可以得到:
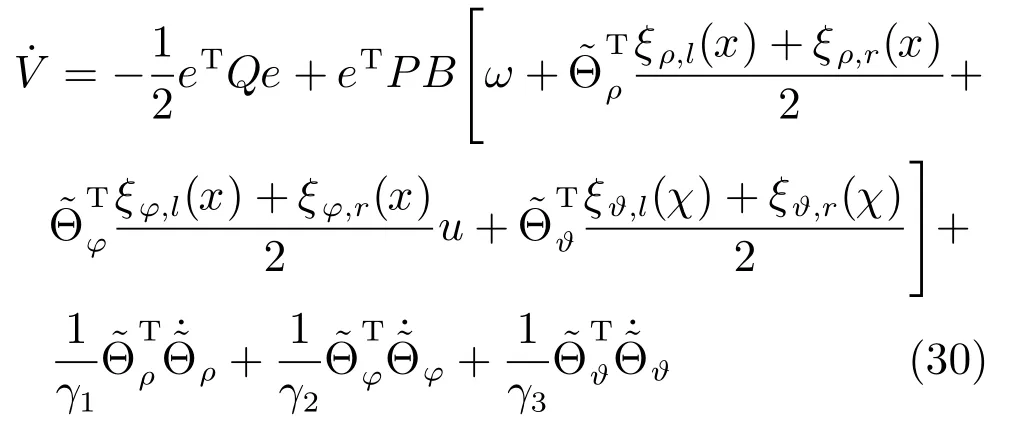
上式经简单整理可得:
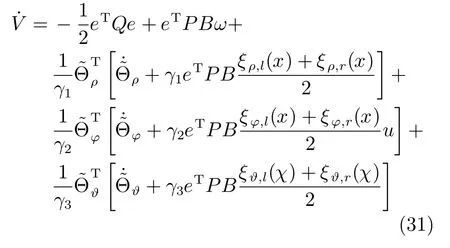
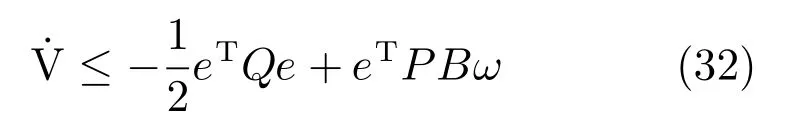
由于矩阵P和矩阵Q为正定矩阵,特征值均大于零,那么以上方程满足:
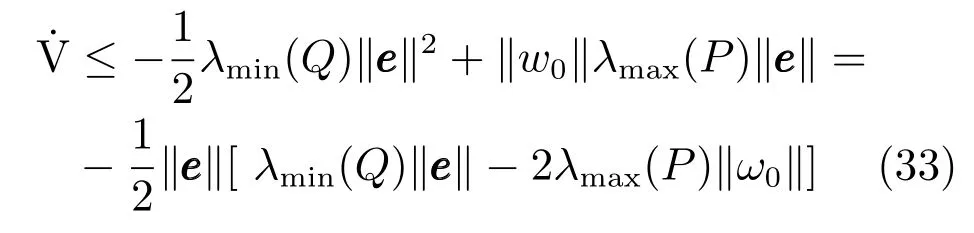
其中,ω0为逼近误差ω的界,λmin(Q)为矩阵Q的最小特征值,λmax(P)为矩阵P最大特征值.

由Lyapunov理论可知,只要误差项大于方程式(34)的右边项,那么跟踪误差就会减小.这也说明跟踪误差的有界性,即:

由式(35)的可知,该系统的跟踪误差大小取决于系统逼近误差的界ω0.由万能逼近特性可知,自适应模糊系统的建模误差是能保证一定的精度.
4 仿真结果与分析
把本文所提出的基于II型模糊逻辑系统的自适应控制器用于图1所示的PEMFC空气供给系统的过氧比控制仿真.本文设计的控制器不需要模型参数已知的条件,只是在控制仿真验证实验时、被控对象模型需用文献[5]中的模型参数.PEMFC空气供给系统的状态空间模型为:
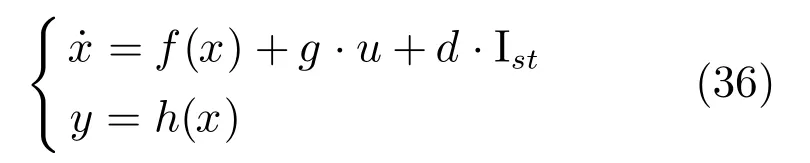
在控制器设计中,为了方便二型模糊集合统一描述和编程,用统一向量x表示.对于控制器(19)中的(x)和(x),设向量x=[x1,···,x6]T;对于(χ),设向量x=χ=[x1,···,x7]T.
步骤1.建立二型模糊逻辑系统
前提变量xi经归一化处理后、取5个如图 4所示的二型模糊集合,用来表示,其相应的高斯隶属度函数选择如下:依据前文第2节的步骤1∼步骤4可建立二型模糊逻辑系统、和.
步骤2.仿真参数选择
在仿真中,被控对象的模型参数按照文献[5]的附录D和E选取;而本文控制器的参数选择采用反复凑试法、直至出现满意的响应.状态变量的初始值基于文献[7]选取为x(0)=[5.4×103,1.5×105,3×10−2,1×10−3,8×10−3,1.25×105];凑试自适应调整参数γ1=102、γ2=10和γ3=102,约束集取Mρ=104、Mϕ=102和Mϑ=103.取k1=60,k2=800,选取正定对称矩阵,解Lyapunov方程(27)可得为一正定对称矩阵.
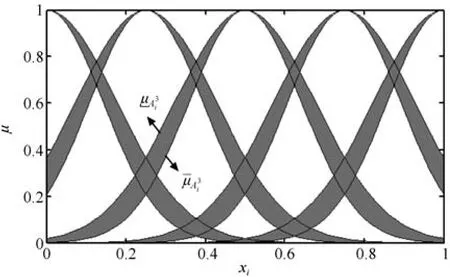
图4 二型模糊系统隶属度函数Fig.4 Membership function of IT2 fuzzy system
步骤3.第一种负载电流情况的仿真
为了验证基于II型模糊系统的自适应控制有效性,首先选取国际文献中常用图5(a)所示的负载电流进行仿真实验.
由式(4)可知,该电流对应的参考过氧比或者理想过氧比λO2,ref如图5(b)实线所示.PEMFC系统过氧比λO2跟踪曲线与跟踪误差e曲线分别如图5(b)虚线和图5(c)所示,图5(d)为输入工作电压.由图5(b)可知,在图5(a)负载电流工况下,基于II型模糊系统的自适应控制器能保证系统过氧比λO2很好地跟踪理想过氧比λO2,ref.由图5(c)可知,该控制器可保证跟踪误差一致最终有界,从而保证了系统具有良好的跟踪性能与稳定性能.
步骤4.第二种负载电流情况的仿真
为了进一步验证基于II模糊系统的自适应控制器的鲁棒性,将第一种电流切换到图6(a)所示频繁变化的负载电流再次仿真实验.PEMFC系统过氧比λO2跟踪曲线与跟踪误差e曲线分别如图6(b)和图6(c)所示,图6(d)为输入工作电压.由图6(b)可知,在6(a)所示的变化频繁的负载电流工况下,基于II型模糊系统的自适应控制器同样可实现对PEMFC空气供给系统的合理控制,使得系统过氧比λO2也能很好地跟踪理想过氧比λO2,ref.由图6(c)可知,在该控制器作用下,跟踪误差也取得了一致最终有界性,从而保证了该系统的稳定性与鲁棒性.
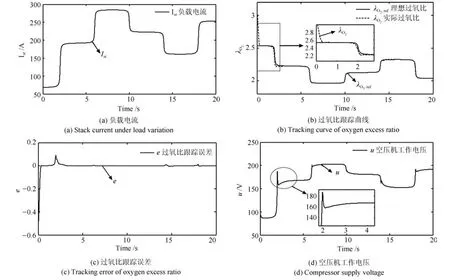
图5 第一种电流情况下的控制器仿真结果Fig.5 The simulation results of controller in current case 1
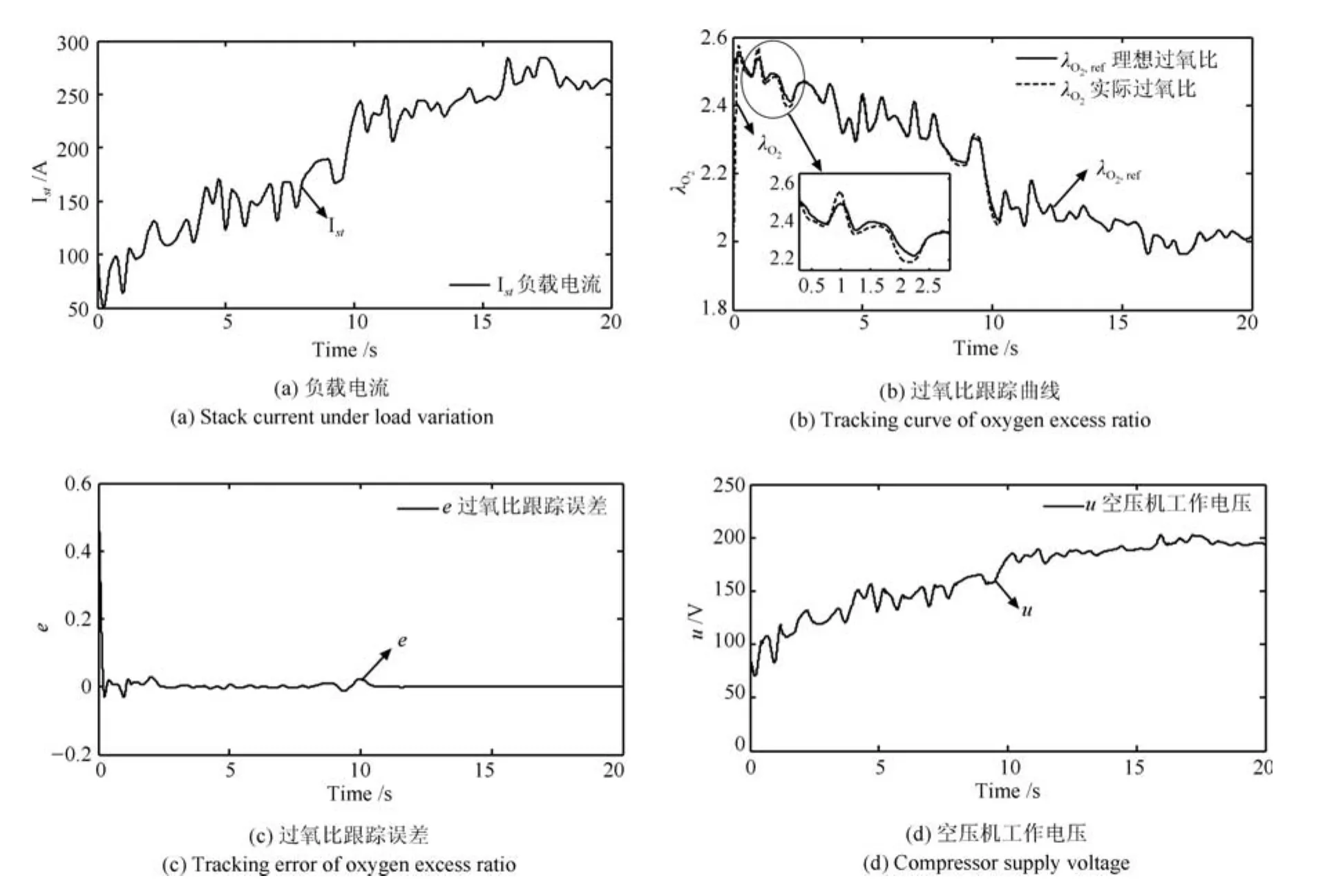
图6 第二种电流情况下的控制器仿真结果Fig.6 The simulation results of controller in current case 2
步骤5.不确定参数的对比仿真
为了进一步验证基于II模糊系统的自适应控制器的自适应特性,将仿真模型中的原始电堆温度Tst=80◦C 切换到Tst=75◦C.在原始温度Tst=80◦C时,采用精确线性化控制器(见附录C)所获得的过氧比λO2跟踪曲线和跟踪误差e曲线分别如图7(a)和图7(b)所示,从图7可知系统获得较好的跟踪效果.在控制器参数不变的情况下,将模型中的原始温度Tst=80◦C切换到Tst=75◦C时,图8(a)和图8(b)是精确线性化控制器作用下所获得的跟踪效果、而图8(c)和图8(d)是本文控制器作用下所获得的跟踪效果.图8(a)和(b)相比于图7(a)和(b)说明精确线性化控制器在模型参数存在不确定的情况下、控制效果变差,而图8(c)和(d)说明本文所设计的控制器即使存在参数不确定,也能获得良好的自适应性能.
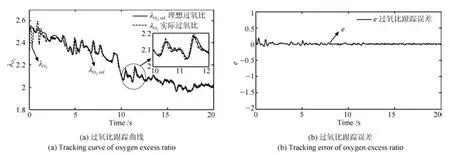
图7 在Tst=80◦C时精确线性化控制器的仿真结果Fig.7 The simulation results of exact linearization controller when Tst=80◦C
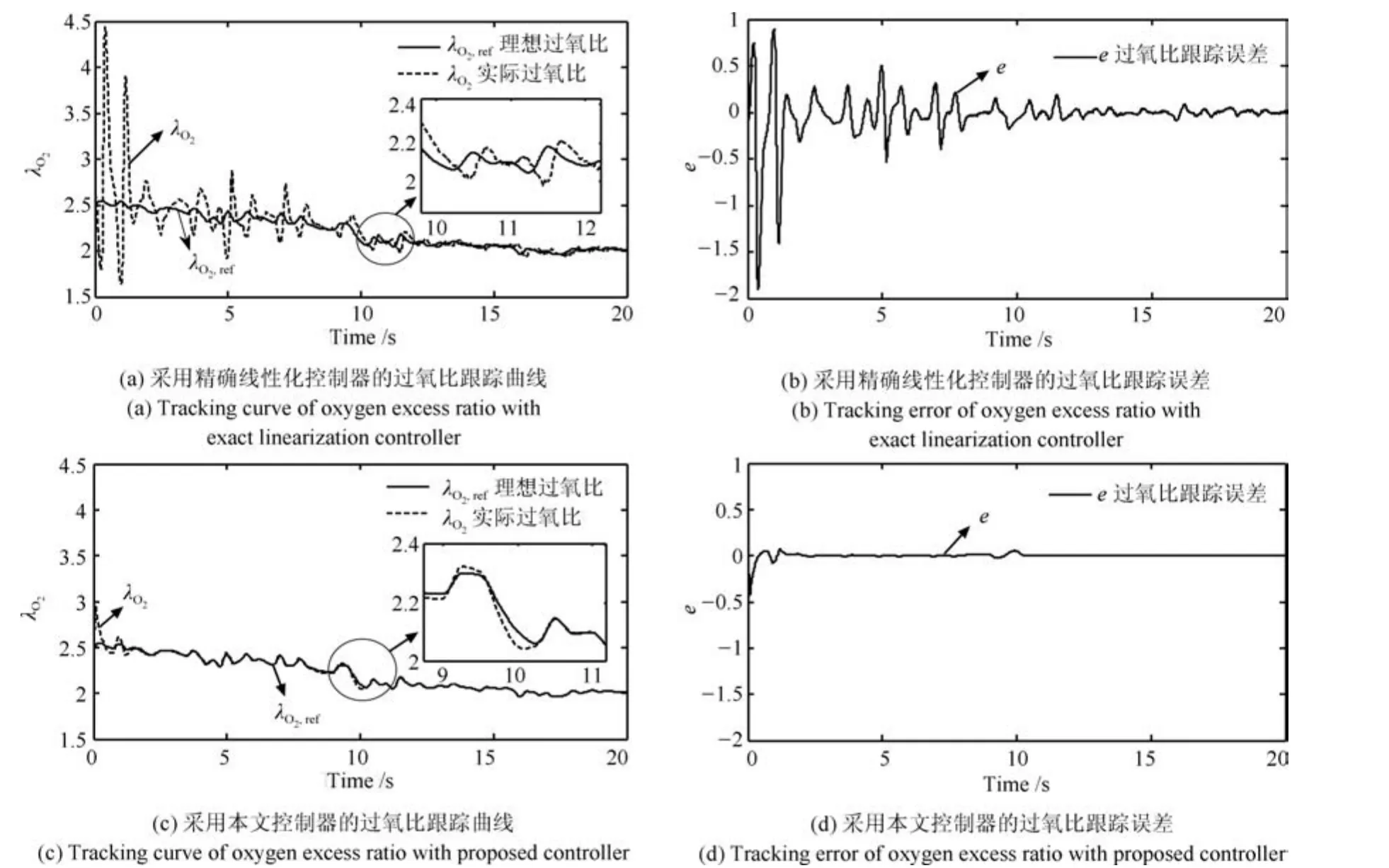
图8 在Tst=75◦C时精确线性化控制器和本文所建议控制器的对比仿真结果Fig.8 The simulation results of exact linearization controller and proposed controller when Tst=75◦C
5 结论
本文针对PEMFC空气供给系统难以实现精准建模,从而造成控制器的设计和系统稳定性分析比较复杂这一难题.提出基于Lyapunov稳定性的自适应控制器设计,其中采用二型自适应模糊系统在线逼近PEMFC系统中的未建模动态,并从Lyapunov函数中导出自适应参数,从而保证了跟踪误差的有界性.从仿真中得出采用该控制器不但可以获得良好的跟踪性能,而且具有良好的稳定性、鲁棒性与自适应特性.进一步的工作是在条件成熟的情况下,将本文的控制方法应用到实际中.
附录A 模型修正
注A1.文献[5]中存在一些明显打印错误的地方:1)在表A1中,从原公式的右边表达式显然可知注入阴极氧气流量WO2,in(x2,x3,x4)和注入阴极氮气流量WN2,in(x2,x3,x4)是变量x2,x4和x5的函数、而非x2,x3和x4的函数,故公式左边需修改成WO2,in(x2,x4,x5)和WN2,in(x2,x4,x5),而方程右边可能是推导失误.2)文献[5]中的状态方程(3)中的Jcm符号不存在,由该文的附录A可知应是Jcp.3)另外,文献[5]状态方程(3)中的应是.4)在文献[5]中的B−B没有定义且该文也没4345有用到,但上表中的流出阴极空气流量却用到B46−B49且在该文附录F中也没有此定义、应是B1−B42当中的某些量,显然是误写.
下面对以上面第一个表达式注入阴极氧气流量WO2,in(x2,x4,x5)为例说明其修正过程:
由文献[7]可知,WO2,in(x2,x4,x5)可表示为:
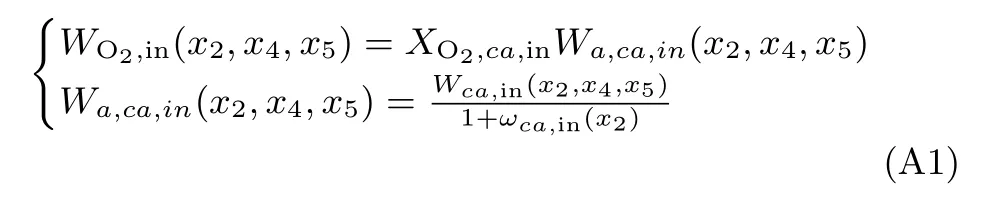
其中,XO2,ca,in为注入阴极空气中的氧气质量分数,Wa,ca,in(x2,x4,x5)为注入阴极干燥空气流量,ωca,in(x2)为注入阴极空气的湿度,Wca,in(x2,x4,x5)为注入阴极空气流量.首先,XO2,ca,in和ωca,in(x2)可分别表示为:

其中,MO2、MN2和Mv分别为氧气、氮气和水蒸气的摩尔质量,yO2,ca,in为注入阴极空气中氧气的摩尔质量分数,pv,ca,in和pa,ca,in(x2)分别为注入阴极的水蒸气压强和干燥空气的压强.接下来,pv,ca,in和pa,ca,in(x2)可分别表示为:
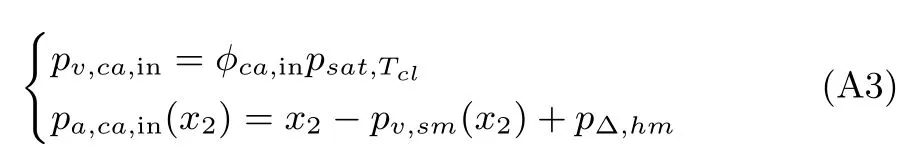
其中,φca,in为注入阴极空气的相对湿度,psat,Tcl为经冷却处理后水蒸气的饱和压强,pv,sm(x2)为供给管道内水蒸气压强,p∆,hm为加湿处理后的水蒸气压强与注入阴极的水蒸气压强之差.再有,pv,sm(x2)和p∆,hm可分别表示为:

其中,patm、φatm和psat,Tatm分别为标准状况下空气压强、空气的相对湿度和空气中水蒸气饱和压强,φdes为加湿处理后的空气相对湿度.
由文献[7](在文献[5]中的参考文献[35])可知,注入阴极空气流量Wca,in(x2,x4,x5)可表示为:
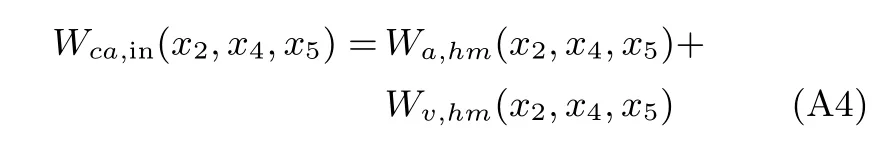
其中,Wa,hm(x2,x4,x5)和Wv,hm(x2,x4,x5)分别为加湿处理后干燥空气流量与水蒸气流量,可分别表示为:

表A1 原公式和修正后公式的对比Table A1 Comparison of original formulas and revised formulas
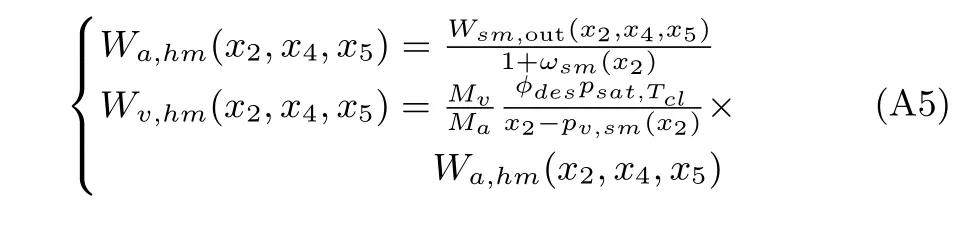
其中,ωsm(x2)为供给管道内空气湿度,Wsm,out(x2,x4,x5)为流出供给管道的空气流量,可分别表示为:
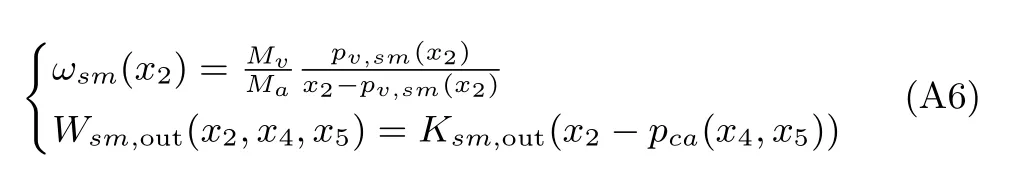
其中,Ksm,out为供给管道孔口常数,pca(x4,x5)为阴极压强.pca(x4,x5)可表示为:
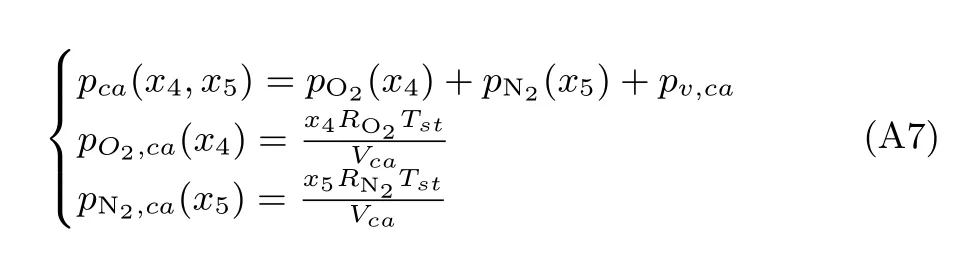
其中,pv,ca、pO2,ca(x4)和pN2,ca(x5)分别为阴极内水蒸气、氧气和氮气压强,RO2和RN2分别为氧气和氮气的气体常数,Vca为阴极体积.
运用式(A2)∼(A7)到式(A1),经简单整理后可得注入阴极氧气的流量WO2,in(x2,x4,x5)为:

结合文献[5]附录C中e(x2)、k(x2)函数的定义和附录F常量B32∼B39的定义,式(A8)可表示为:
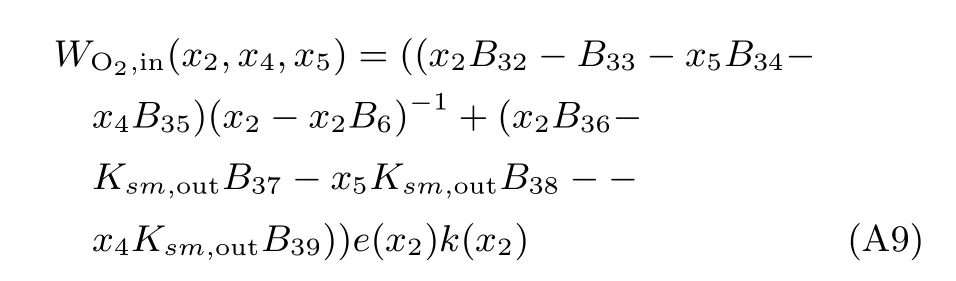
由于篇幅原因,其余公式更正过程不再赘述.
附录B 状态空间函数

其中,在参考文献[5]中的函数Tcp(x2),Wcp(x1,x2),Tsm(x2,x3),Wsm,out(x2,x4,x5),WN2,out(x2,x4,x5)和Wrm,out(x6)的推导与整理均正确无误.但函数WO2,in(x2,x4,x5),WO2,out(x4,x5,x6),
WN2,in(x2,x4,x5),τcm(u,x1),τcp(x1,x2)和Wca,out(x4,x5,x6)的推导与整理存在错误.本文结合文献[7]中的基本物理方程对以上错误函数进行复合修正与整理,修正结果见前面的附录A.
附录C 精确线性化控制器求解
仿真对比实验需要用到精确线性化控制器.由于系统模型的复杂性、很难手工求解,为此需要借助软件计算工具求解.精确线性化控制器中的ρ(x)、ϕ(x)和ϑ(χ)函数可用Matlab软件中的mupad工具箱求解,其计算过程指令如下:
步骤1.在Matlab命令窗口输入“mupad”指令、打开mupad工具箱,结合本文与文献[5]附录将正确的和h(x)函数编写到mupad工作空间.
步骤2.首先通过以下微分指令函数,求解式(6)中Lfh(x)和Ldh(x),即:
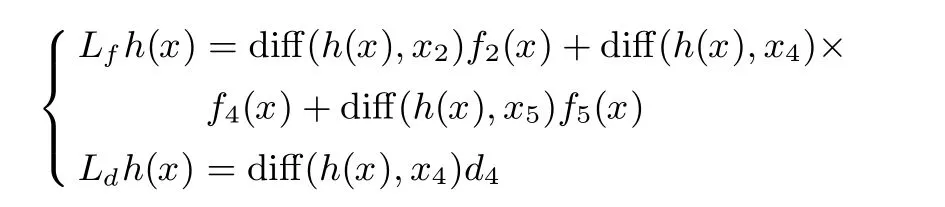
步骤3.接下来通过以下微分指令函数,求解式(7)中,即:
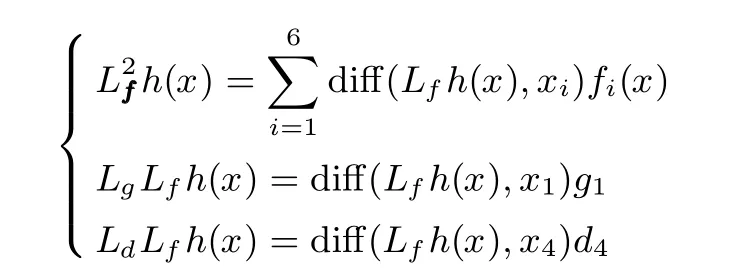
其中,g1和d4为向量g和d的分量.
步骤4.文献[11]认为实际中的Ist电流是缓慢变化的、可视作常数处理,用以下微分指令求解Ldh(x)关于时间t的导数,即:
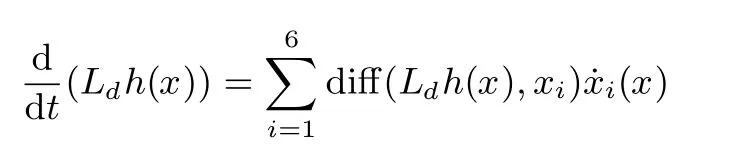
步骤5.最后综合步骤1到步骤4,精确线性化控制器中的ρ(x)、ϕ(x)和ϑ(χ)函数表达式可表示如下: