基于大地经纬度的二维TDOA无源定位

马方立，徐扬，徐鹏

（1. 西南交通大学信息科学与技术学院，四川 成都 611756；2. 四川省无线电监测站，四川 成都 610052；

3. 系统可信性自动验证国家地方联合工程实验室，四川 成都 610031；4. 西南交通大学数学学院，四川 成都 611756）

1 引言

到达时间差（TDOA, time difference of arrival）无源定位是利用布设在不同地点的多个接收点同时接收某一信号源发出的信号，并通过测量接收点两两之间的信号到达时间差来确定信号源位置的方法。TDOA无源定位研究始于20世纪60年代，采用三维直角坐标[1]；Stilp[2]于20世纪90年代将此技术用于公众移动通信网终端定位。

由于时差测量技术的进步，TDOA无源定位技术在移动通信网定位、跟踪[3]和无线电监测定位这2个领域的应用日益广泛。TDOA定位方法本质上通过测量无线电波到达时间差来表示到达距离差，从而实现定位，故距离计算的准确度与定位的准确度密切相关。现有文献[1-12]多以平面直角坐标表示，往往假设某一监测站点为坐标原点，例如，文献[10]“令Ri,1为待测目标到第i个定位基站和第一个定位基站（本文定义为中心基站）之间的距离差”；文献[13]提出“需要将大地经纬度坐标转换为平面直角坐标，计算出X、Y后，再把X、Y转换为经纬度坐标。由于地球不是一个标准的球体，平面直角坐标系和地图坐标系转换后会有误差，误差有时会达到几千米”，并指出“使用百度、谷歌、高德中某一家的地图，就使用某一家的转换算法”。

文献[14]研究了TDOA定位中经纬度与平面坐标转换方案，分析了地球在椭球模型下的几种投影算法，但未见直接利用大地经纬度进行TDOA定位的研究文献。

在卫星导航日益普及的今天，大地坐标是易于获取并广泛使用的坐标，地球上任意一点的位置可以用大地经度、大地纬度和大地高表示。为了提高定位精度、减少误差，本文提出了基于大地坐标的2种二维TDOA无源定位数学模型，即球面精确计算模型和球面近似计算模型，并与传统的平面直角坐标TDOA无源定位模型进行比较。

2 二维TDOA定位的现有模型

现有的二维 TDOA无源定位模型多基于平面直角坐标系，如图1所示。

Mi(xi,yi)和Mj(xj,yj)是配置于基线MiMj两端的2个监测站点，它们与信号源S(x,y)的距离分别为di和dj，单位均为km。这个距离可以表示为di=cti和dj=ctj，则有

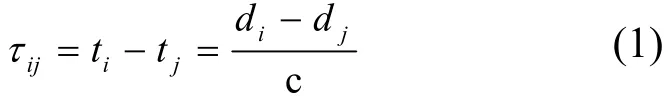
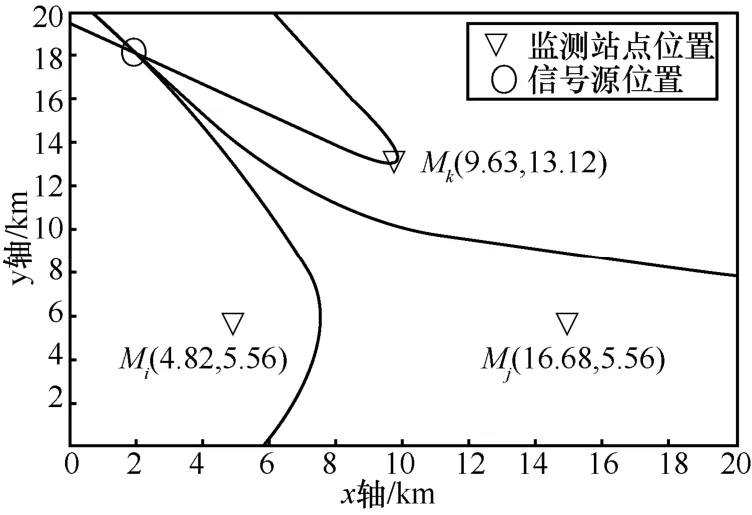
图1 平面直角坐标系的TDOA定位

其中，c=3×108m/s是电波在空中的传播速度；ti和tj分别是电波由辐射源传播到监测站Mi和Mj的时间，单位为s；τij为信号到达2个监测站的时间差，单位为 s。式(1)由电波传播速度计算式推导而来，是TDOA的基本公式，它表明无线电波的到达距离差等价于到达时间差。

对于上述距离单位表示的二维平面直角坐标，TDOA无源定位方程为

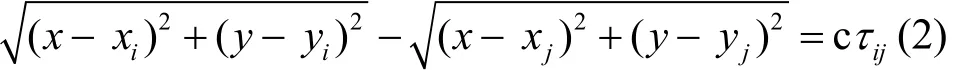
如果有N个监测站点能够接收到某一信号，且能够测得电波到达这些站点之间的时间差，那么最多可以得到由个方程组成的方程组，即

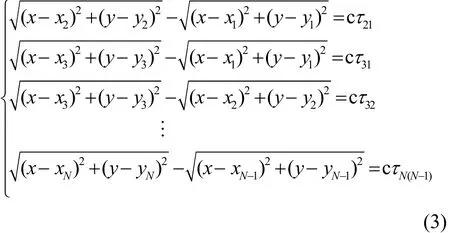
如果以第一个站点为参考点，仅仅测量其他站点与第一个站点的信号到达时间差，则最多可以得到(N-1)个方程组成的方程组，即

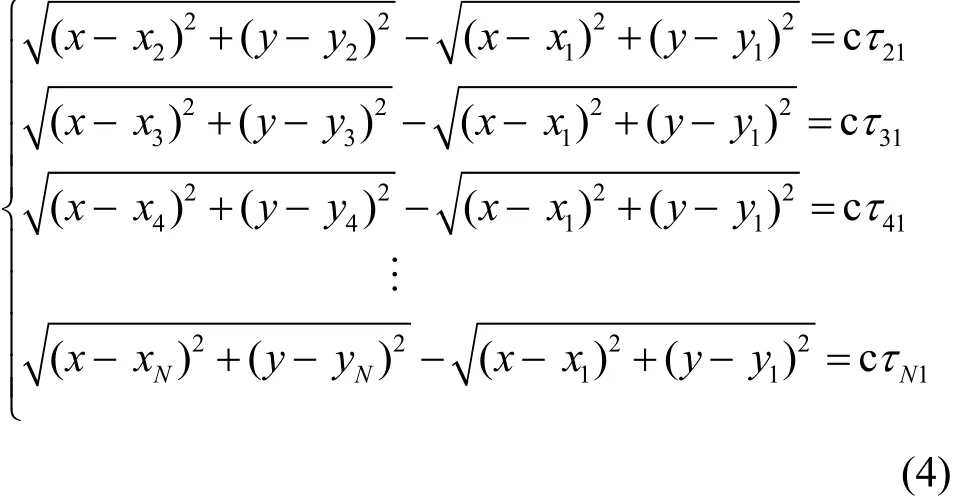
为简化起见，以下其他模型均只列出以第一个站点为参考点的情况。

从式(2)～式(4)可以看出，现有二维TDOA无源定位模型是以距离为单位表示的二维平面直角坐标，不直接使用大地经纬度坐标。直接采用大地经纬度坐标将带来方便性，因为大地经纬度容易获取且全球统一，而二维直角坐标一定是球面的某种投影，与投影方法相关。接下来，将探讨如何直接利用大地经纬度坐标进行TDOA无源定位。

3 大地经纬度表示的二维TDOA定位模型

大地经纬度是用大地经度、大地纬度表示地面点位置的球面坐标。一种简化的地球模型是地球球体模型，该模型表面是一个球面，平均球半径为6 371.1 km[15]，在经线和赤道上1°代表的地球大圆长度为111.2 km，将地面点P的位置用经度和纬度表示。大地经度是通过该点的大地子午面与通过格林尼治天文台的起始大地子午面之间的夹角，规定以起始子午面起算，向东从0°～180°称为东经（E），向西从 0°～180°称为西经（W）。大地纬度是通过该点的法线与赤道面的夹角，规定由赤道面起算，由赤道面向北从 0°～90°称为北纬（N），向南从 0°～90°称为南纬（S）[16]。

本文采用地球球体模型，通过大地坐标计算地球表面任意两点之间的距离，可用球面精确计算法、球面近似计算法[17]和地图投影法[16]求解，并建立对应的球面精确计算模型、球面近似计算模型和球面正轴圆柱投影模型。

经纬度定位的TDOA定位如图2所示。令Mi(λi,φi)和Mj(λj,φj)为以经纬度表示的 2 个监测站点坐标，S(λ,φ)为信号源坐标，λ为大地经度，φ为大地纬度。

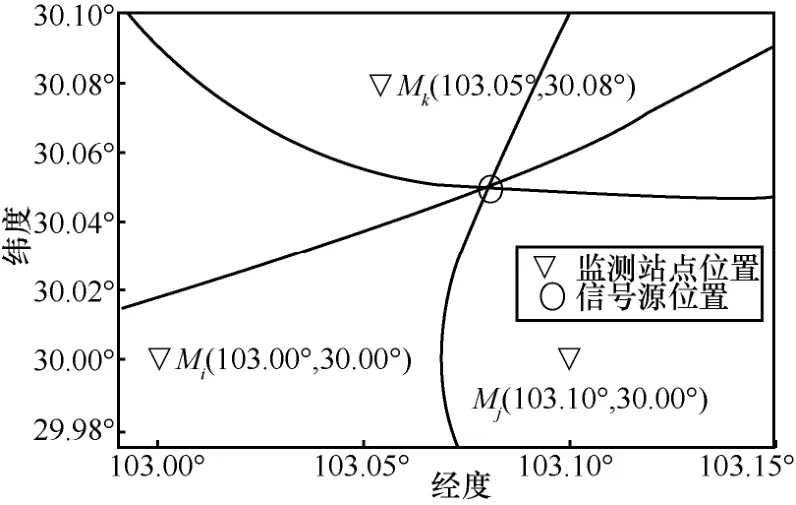
图2 经纬度坐标的TDOA定位

3.1 球面精确计算二维TDOA定位

球面上任意两点之间的最短距离是以球心为圆心的大圆上的短弧[16]。根据球面余弦公式，可得信号源S(λ,φ)与监测站点Mi(λi,φi)的距离di为

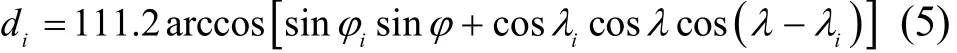
式(5)是地球上任意两点间最短距离的精确计算公式，含有超越函数。其中111.2是在经线上和赤道上1°代表的地球大圆长度，单位为km；λ和φ分别表示大地经度和大地纬度。

由式(1)和式(5)可知，无线电波从地球上任一地点X(λ,φ)，分别到达监测站点Mi(λi,φi)和Mj(λj,φj)的时间差τij为

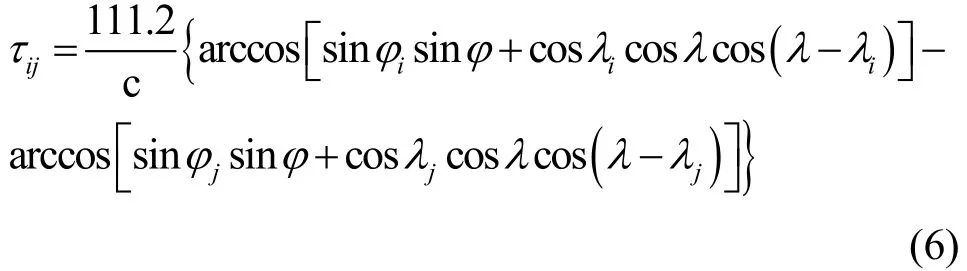
式(6)是无线电波从任一地点X(λ,φ)分别到达监测站点Mi(λi,φi)和Mj(λj,φj)的时间差的精确计算式。

如果以第一个站点为参考点，则最多可以得到由(N-1)个方程组成的方程组，即

式(7)含有三角函数和反三角函数，属于超越方程组，与经典的二维直角坐标TDOA定位方程组(4)差别很大，难以采用已有的TDOA定位求解方法解算。

3.2 球面近似计算二维TDOA定位

大地坐标距离近似计算二维 TDOA定位模型是基于球面距离近似计算方法的TDOA定位模型。球面距离近似计算方法如下。

通常在较小的尺度上，将大地（地球表面的局部区域）视为平面，以勾股定理计算任意两点之间的距离，再以这两点的经度差大圆弧长和纬度差大圆弧长为直角边，两点之间的距离为斜边，其经度和纬度单位角度所代表的距离是不同的。在任何纬度，这种方法的误差都不大[17]，计算方法为

式(8)是地球上任意两点间最短距离的近似计算公式。经线上1°代表111.2 km，而纬线上1°代表的距离却随纬度的不同而变化，为

令r表示经度差大圆弧长随纬度变化的尺缩因子，表示经度差大圆弧长随纬度变化的平均尺缩因子，则有

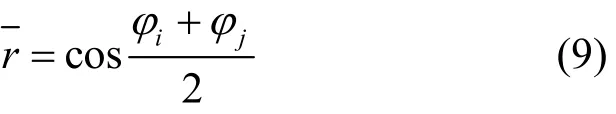
可近似地设φ0为所在区域的纬度值取整，则有

设纬线上1°代表的距离为Δd，表1列出了纬线上每隔5°的Δd值和r值。从表1可知，不同纬度下经度差1°时距离有明显差别。

表1 纬度上每隔5°的Δd值和r值

由式(1)、式(8)和式(10)可知，如果以第一个站点为参考点，则有方程组(11)，其中N≥3。

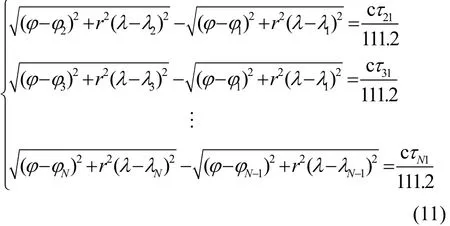
从形式上看，式(11)与式(4)很相似，主要差别在于信号源与监测站点之间的经度差需要乘以尺缩因子r，因此，完全可以采用已有的TDOA定位求解方法解算。

3.3 球面正轴圆柱投影二维TDOA定位

球面正轴圆柱投影有等距离投影、等角度投影、等面积投影这3种[16]，其中球面等角度正圆柱投影也叫Web Mercater投影[11]。按无线电定位领域的惯例，将投影平面的横轴作为x轴、纵轴作为y轴，则3种球面正轴圆柱投影的横坐标的投影计算式均为

其中，111.2表示经线上1°代表的距离，单位为km；λ为经度。

而纵坐标的投影计算式不同，其中，球面等距离正圆柱投影公式为

其中，ϕ为纬度。

球面等角度正圆柱投影计算式为

球面等面积正圆柱投影计算式为

将式(12)和式(13)代入式(2)，可得球面等距离正圆柱投影TDOA定位方程组为

式(16)与式(4)在形式上完全相同，可通过球面等距离正圆柱投影式(12)和式(13)相互推导。可见，球面等距离正圆柱投影 TDOA模型与经典的二维直角坐标 TDOA模型等价，完全可以采用已有的TDOA定位求解方法解算。

将式(12)和式(14)代入式(2)，可得球面等角度正圆柱投影TDOA定位方程组为

式(17)含有对数函数和正切函数，属于超越方程组，与经典的二维直角坐标TDOA定位方程组(4)差别很大，难以采用已有的TDOA定位求解方法解算。

将式(12)和式(15)代入式(2)，可得球面等面积正圆柱投影TDOA定位方程组为

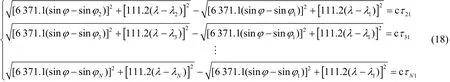
式(18)含有正弦函数，属于超越方程组，与经典的二维直角坐标TDOA定位方程组(4)差别很大，难以采用已有的TDOA定位求解方法解算。

3.4 最优化建模及求解方法

对于定位方程的求解，有绘图法、解析法和递归法，其中，绘图法需要人工读数；解析法如两步加权最小二乘法（Chan方法）等，仅适用于平面直角坐标，可用于按平面直角坐标计算的球面近似计算模型；递归法如Taylor级数迭代法（NLS）等[3]，存在收敛性问题，因此，常规的方法不适用于含有超越函数的球面精确计算模型、球面等角度正圆柱投影模型和球面等面积正圆柱投影模型。本文采用基于无约束非线性规划的最优化TDOA方法[6,11]。

TDOA最优化目标函数的通式为

其中，f(λ,φ)为以信号源经度λ和纬度φ为自变量的最优化目标函数，dp(λ,φ)和d1(λ,φ)分别为第p个和第一个监测站点到信号源的距离。

由式(6)和式(19)，可得基于球面精确距离计算的二维TDOA模型的最优化目标函数式为

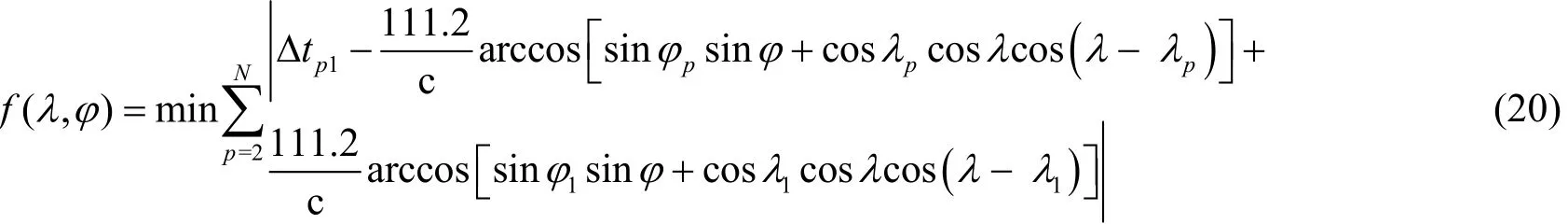
由式(8)和式(19)，可得基于球面近似距离计算的二维TDOA模型的最优化目标函数式为

由式(14)和式(19)，可得基于等距离正圆柱投影的二维TDOA模型的最优化目标函数式为

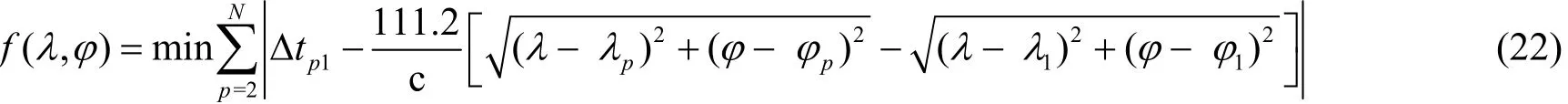
由式(18)和式(19)，可得基于等角度正圆柱投影的二维TDOA模型的最优化目标函数式为

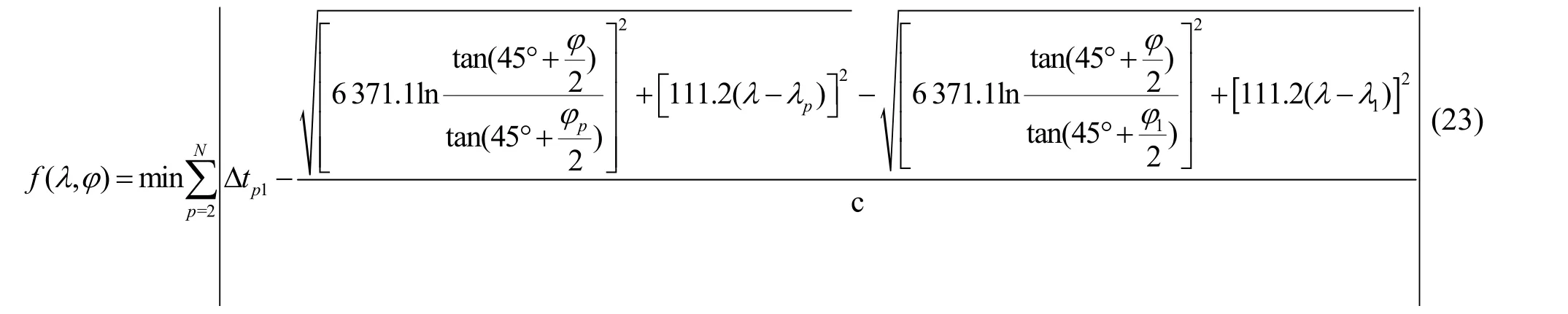
由式(14)和式(19)可得，基于等面积正圆柱投影的二维TDOA模型的最优化目标函数式为

适合无约束非线性规划的一些最优化方法，可能存在少量的不收敛点[11]，对于含有超越函数的球面精确计算模型、球面等角度正圆柱投影模型和球面等面积正圆柱投影模型也不适用。因此，为避免不同算法可能带来的收敛性、局部极值、精确度差别等问题，采用网格逐点搜索法[11]求解。

考虑到超短波电波传播的距离通常不超过50 km，以TDOA定位网络的几何中心或者接收到最强信号的站点M0(λ0,φ0)为中心，从东、西、南、北各约50 km的范围内进行逐点计算，找出使最优化目标函数f(λ,φ)取最小值的坐标点，即信号源的位置。具体地，搜索范围从经度到，从纬度到，步长分别为和。利用Q×Q网格计算顶点和交叉点，共(Q+1)×(Q+1)个点。定位误差均值一般不超过搜索步进的2倍，并且不会出现不收敛的情况。如果要提高定位精度，可减小搜索步长。

4 数值验证

本文通过仿真，比较基于3种距离计算方法的TDOA定位模型在不同尺度、不同纬度下的性能差别。仿真参数设置如表2所示。

对于大地坐标下的球面精确计算定位模型、球面近似计算定位模型、等距离正圆柱投影定位模型（等价于经典的平面直角定位模型）、等角度正圆柱投影定位模型和等面积正圆柱投影定位模型，在纬度上每隔5°进行1 km、10 km、100 km共3种尺度的基线（站距）的仿真，以逐点计算的网格搜索方法，当不考虑时差测量误差时，3种尺度下的定位误差结果相同，均如图3所示。

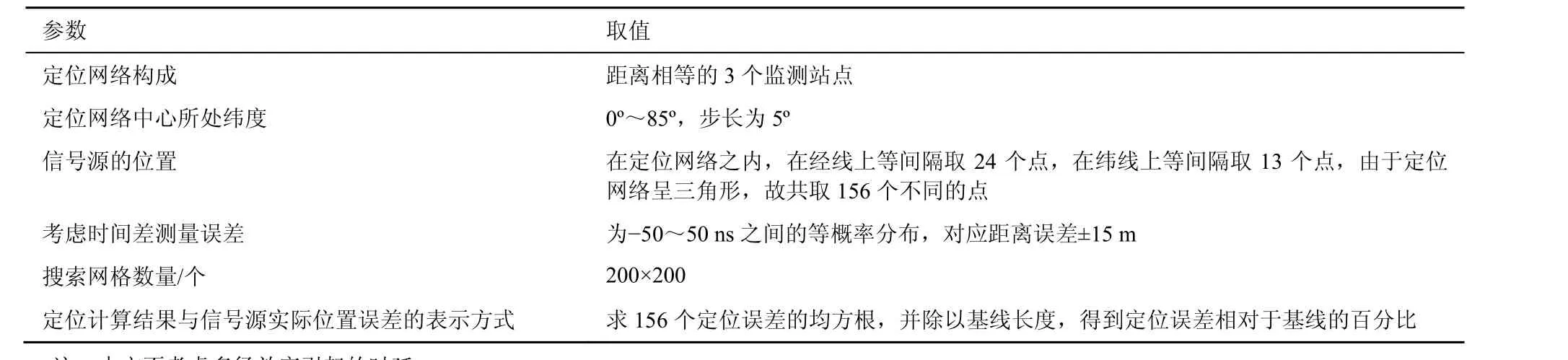
表2 仿真参数设置

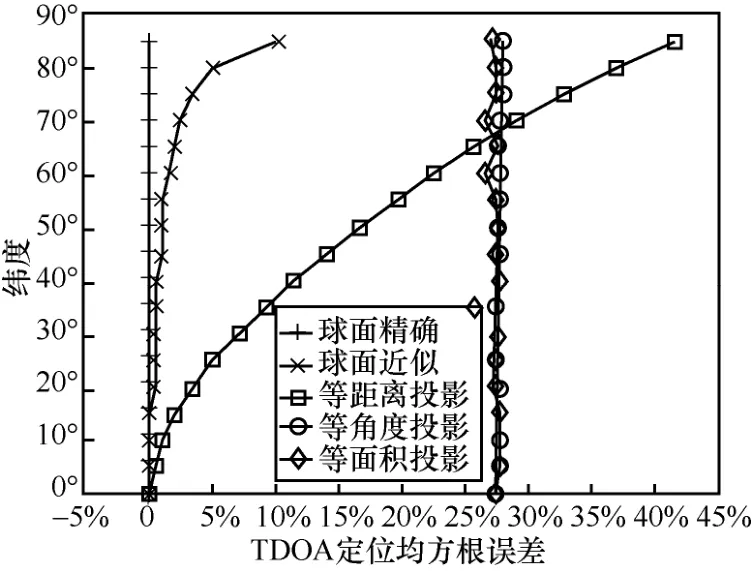
图3 当不考虑时差测量误差时，3种尺度下的定位误差比较

从图3可以看出，在不考虑时差测量误差的情况下，等角度正圆柱投影TDOA定位模型和等面积正圆柱投影TDOA定位模型的定位误差比较大，在任何纬度时均在26%左右，不可用；球面精确计算TDOA定位模型的定位误差极小，可用；球面近似计算TDOA定位模型的定位误差较小，在低纬度时定位误差在 0.54%以内，在中纬度时定位误差在0.54%～1.6%，在高纬度时定位误差高于10%，可用；等距离正圆柱投影TDOA定位模型（等价于经典的平面直角TDOA定位模型）在低纬度时定位误差在7.1%以内，在中、高纬度时定位误差随纬度增加，最大可超过41%，因此只在低纬度地区可用。

对于大地坐标下的球面精确计算 TDOA定位模型、球面近似计算TDOA定位模型、球面等距离正圆柱投影TDOA定位模型（等价于经典的平面直角TDOA定位模型），在纬度上每隔5°进行1 km、10 km、100 km共3种尺度的基线（站距）的仿真，以逐点计算的网格搜索方法，获取3种尺度下的误差结果。当考虑时差测量误差时，3种基线尺度下3种模型的定位误差比较如图4所示。

从图4可以看出，当考虑时差测量误差时，3种可用或者在低纬度地区可用的TDOA定位模型中，在1 km基线尺度时，即最大距离测量误差与基线长度之比为 1.5%时，带来 1.1%～1.3%的均方根误差；在10 km以上基线长度时，即最大距离测量误差与基线长度之比不到0.15%时，影响可以忽略。因此，球面精确计算TDOA定位模型与球面近似计算 TDOA定位模型的定位误差也受时差测量误差的影响，基线越短，影响越大。球面精确计算TDOA定位模型误差极小，球面等距离正圆柱投影TDOA定位模型误差最大，球面近似计算TDOA定位模型误差较小；球面近似计算TDOA定位模型的定位误差随纬度升高而增加，而球面精确计算模型的定位误差与纬度无关。原因是所用的球面上2点之间的距离计算方式不同，球面精确计算TDOA定位模型采用球面三角函数方式，而球面距离近似TDOA定位模型采用类似勾股定理的近似计算方式。

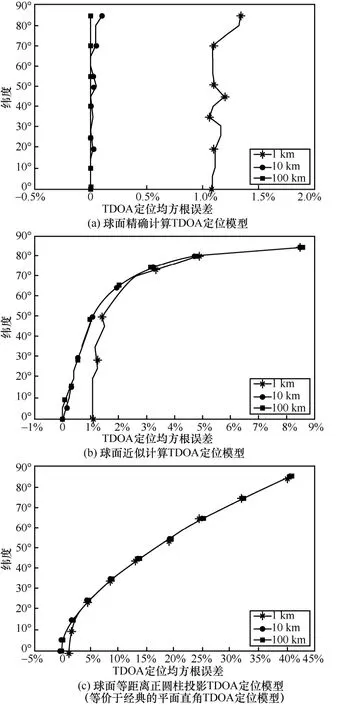
图4 当考虑时差测量误差时，3种基线尺度下3种模型的定位误差比较

5 结束语

基于平面直角坐标与球面坐标的差异，本文提出了基于大地经纬度的几种二维 TDOA无源定位数学模型。通过建模和仿真实验，得到以下结论：球面精确计算TDOA定位模型误差极小，定位误差与纬度无关；球面近似计算TDOA定位模型误差较小，定位误差随纬度升高而增加；等距离正圆柱投影 TDOA定位模型等价于传统的平面坐标 TDOA定位模型，在低纬度定位误差较小，但大于球面近似计算TDOA定位模型，可用，在高纬度地区定位误差大，不可用；等角度正圆柱投影TDOA定位模型和等面积正圆柱投影 TDOA定位模型在不考虑时差测量误差情况下的定位误差就比较大，在任何纬度时均在26%左右，不可用。通过对1 km、10 km、100 km这3种基线尺度进行比较可知，定位误差受到达时差测量误差影响，基线越短，影响越大。因此，当需要精确计算时，应采用球面精确计算TDOA定位模型，但其含有超越函数，计算复杂度高，难以采用已有的TDOA定位求解方法解算；当采用近似计算时，宜采用球面近似计算TDOA定位模型，在低纬度也可采用等价于传统的平面坐标 TDOA定位模型的等距离正圆柱投影TDOA定位模型，计算复杂度均低，可采用已有的TDOA定位求解方法解算。

更加精确的地球表面模型是椭球面模型，对应椭球面距离精确计算TDOA模型。由于地球的扁度仅为，通常在不超过100 km的超短波传播尺度范围内，精度的提高不明显，而计算的复杂程度会大大提高。