数形结合在小学中段数学教学中的实施策略分析

连桥娣

摘 要 在当前的小学数学教学，使用数形结合的教学方法对提高小学生理解数学概念和解决数学问题非常重要，能把复杂的问题简单化，抽象的问题形象化，有助于学生理解和运用数学知识，也可以刺激学生的学习兴趣，增强学生对数学知识的理解和记忆从而提高学生的数学素养。

关键词 数形结合 小学数学 实施策略

中图分类号：G623.5文献标识码：A

数学是由两个概念构成的，一个是数，一个是形，数抽象，形直观。数学就像一棵大树，它是由“数”和“形”这两类基本东西里生长出来的并能长出千奇百怪的分枝和花朵。数形结合是抽象与直观、思维与感知的结合。正如华罗庚先生所指出的：“数与形本是相倚依，怎能分作两边飞，数缺形时少直观，形少数时难入微。”美国数学家斯蒂恩说：“如果一个特定的问题可以转化为一个图形，那么思想就整体地把握了问题，并能创造性思索问题的解法。”从这两句话中充分体现出数形结合对数学教学起着非常重要的作用，把数形结合思想贯穿在学习数学过程的始终，是学好数学的关键所在。

长期以来，由于受传统化教学的倾向，小学数学教育存在着重知识、轻思想方法，过分重视数学的抽象性、逻辑性，却使数学自成体系，而忽视了数学与小学生关系的建立，结果造成数学教育的内容笼杂、单调且重复性强。致使小学生获得的知识是孤立的、片面的、僵化的。小学生从一开始接触数学，就学会死记硬背，感受不到学习的乐趣，甚至产生畏惧与厌烦。三四年级的学生已经具备初步的逻辑思维能力，但仍以形象思维为主。这就需要教师深挖教材，在设定数形结合的目标时要从低年级的感悟体验向有意识的引导学生主动形成数形结合的方法。这样更符合儿童的思维发展规律。数形结合对教师来说是一种教学方法、教学策略，对学生来说是一种学习方法，如果长期渗透，运用恰当，则使学生形成良好的数学意识和思想。下面结合课堂教学，谈谈数形结合在小学中段教学的具体实施策略。

1在数学概念教学方面的实施策略

对于小学生来说，概念教学是一个重点也是难点，学生只有充分理解了概念才能运用概念解决数学题。小学生普遍对于直观的、具体的图形和事物比较感兴趣，也比较容易接受，而对于很多抽象的数学概念兴趣不浓，想要让他们理解就变得很困难，而图形作为一种直观显示的重要方法，能使比较抽象的概念转化为清晰、具体的事物，学生容易掌握和理解。

例如：四年级“平均数”一课的教学。教科书借助一个记忆游戏，结合淘气5次游戏所记住的数字数目统计表，提出平均每次记住6个数字是怎么得出来的？“平均数”的计算不难，难在理解其意义。让学生经历一组数据中心点的产生过程，有助于学生理解平均数的概念。用图形呈现了“移多补少的方法“如图1所示，让学生体会这个过程，通过图形的直观展示，学生对平均数的产生过程有了切实的体会，从而对平均数反映一组数据的一般水平也就有了更深刻的认识。

又如：在分数的初步认识中，通过具体的形的操作与实践，让学生充分理解“平均分”，几分之一，几分之几等数学概念，掌握运用分数大小的比较，分数的意义，分数的加减等，使数形紧密地结合在一起，把抽象的数学概念直观地呈现在学生面前，帮助学生理解掌握分数的知识。

2在算法理解方面的实施策略

小学数学内容中，有相当部分的内容是计算问题，它往往能体现一名学生的思维能力，但在计算课的教学过程中我们可能经常会遇到各种各样的问题，比如算理讲了几遍但学生仍然不是很明白等等问题。面对这样的教学现状并不是没有办法，数形结合就是其中的方法之一，下面就将数形结合在算法理解方面的实施策略联系小学中段数学课本内容加以举例具体说明。

2.1笔算方面的应用

在北师大版三年级上册《植树》一课中，要学生掌握两位数除以一位数的口算方法，并能正确地进行计算。例题内容是有36颗树苗，分给3个班，平均每班分到多少棵树苗？你会列算式吗？谁能试一试？（36？）你能说说这个算式是什么意思吗？我没有急着让学生去计算，在黑板上先画出3捆加6棵树苗（1捆代表10棵树苗），每组分1捆，可以分10棵。再把6棵树苗也平均分，每组2棵，10加2就是12棵。 我们可以用这三个算式表示分树苗的过程： 30？=10、6？=2、10+2=12。

可以看到结合图来讲，这里的许多难点问题就可以迎刃而解，不必为枯燥的算理而反复地讲。

又如在12X13两位数乘两位数时，由于学生第一次接触笔算方法，对于其中的算理不是很明确。此时，引导学生借助点子图，用PPT演示笔算过程。整个笔算过程主要分三步完成，第一步用个位去乘第一个乘数，所得的积是36，通过追问：36表示哪些点子？引导学生把算式和点子图联系起来，顺利地找到相应的点子图部分。第二步用十位去乘第一个乘数，所得的积是120。由于之前的经验，学生很自然地想起点子图，并找到相应的点子图部分。第三步把两部分积合起来得到156，也是就是整个点子图。有了形象、直观的点子图帮助学生梳理其中的算理，学生们学得轻松、扎实。最后通过同桌之间互相说说，进一步巩固算理。

2.2在时间的计算方面的应用

《时、分、秒》是在课本中间出现的内容，有相当一部分是学生比较熟悉的，也很感兴趣。但在时间计算方面上却出现了不会算的情况。比如：一列火车3：40开出，于5：10到达某站，问：经过多长时间？不会算的原因就是在讲新课的时候说过：经过时间=到达时间―开始时间，學生反映10减40没法算，但课本上讲的是同一小时内的时间计算。这时我们就画了一个“钟表图”，看着钟表，再有20分就是4：00，再从4：00～5：10有70分钟，两部分相加就是经过的90分钟。通过这样直观的看，避免了抽象的去想，学生感到了学习知识的快乐。

2.3在分数的计算方面的应用

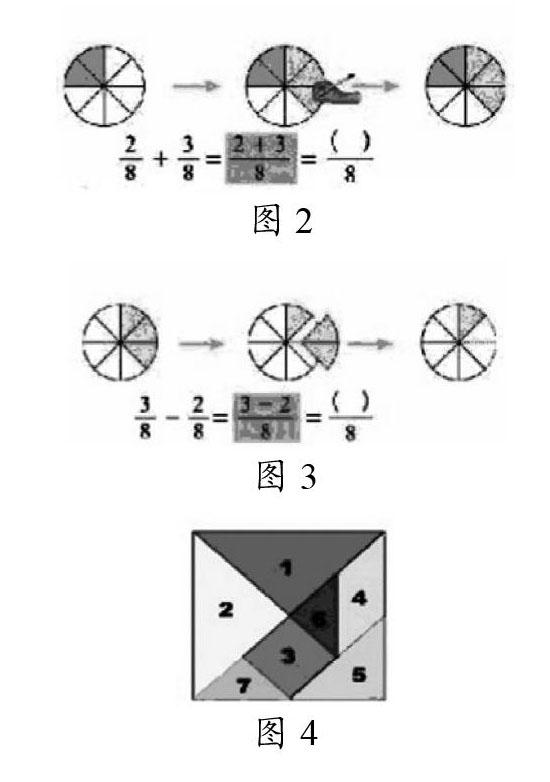
图2所示的分数计算，借助面积模型图可以直观地得到运算结果为5/8，也就是说2个1/8加上3个1/8等于5个1/8，就是5/8。此时可以创设其他分数算式：1/4+2/4=？让学生动手画示意图并说一说。肯定学生说的有道理的方法。又如图3所示3/8-2/8=？归纳同分母分数的计算方法：分母不变，分子相加减。

图4是由七巧板拼成的正方形，你能提出数学问题吗？如：①和②合起来是整个正方形的几分之几？⑤是整个正方形的几分之几？③④⑥⑦合起来是整个正方形的几分之几？此题渗透了数形结合的思想。把分数的意义和运算融合，解决同分母分数的相加，也体现了异分母分数相加的意义。利用数形结合的方法，学生能更好地理解，知其然，知其所以然。

这些示例充分显示出了数形结合在分数计算上的优势。

3在解决问题过程中的实施策略

例1：妈妈的年龄是小芳的4倍，妈妈比小芳大27岁，妈妈和小芳各多少岁？这种题对于三年级学生来说，往往较难解决，但如果老师能够充分重视引导学生在读懂题目的基础上，画出线段图，则大部分学生都能够很顺利地解决。

从线段图中，我们可以形象地看出，小芳的年龄用1份线段表示，妈妈的年龄就可以用这样的4份表示，妈妈比小芳大的27岁则是这样的3份，由此可以引导学生求出1份线段表示的年龄是：27？=9（岁），即小芳的年龄是9岁，妈妈的年龄则是：9？=36（岁）。

例2：一篮鸡蛋，第一次拿走1/2，第二次又拿走剩下的1/2，最后篮子里还有4个鸡蛋。你知道原来这个篮子里有几个鸡蛋吗？（三年级习题）

这道题中单位“1”的量发生变化，第一次是把“整篮鸡蛋”看作单位“1”的量，第二次把“剩下的鸡蛋”看作单位“1”的量，因此学生在解答时往往会感到困难。只要运用数形结合的思想帮助弄清题意，这道题就简便多了。画线段图如下：

从上述线段图中可以很清楚地看出，拿走剩下的1/2，还有4个鸡蛋，那么第一次拿走后“剩下的鸡蛋”的数量应该是4个的2倍，即8个。所以整篮鸡蛋的数量就是8个的2倍，即16个，列式为4？？=16（个）。如此抽象的思维有了“形”这个桥梁作为依托，思考起来既省时又省力。

4在识图方面应用数形结合的策略

三年级学生学习长方形和正方形的周长和面积计算方法后，基本上能正确计算长方形和正方形的周长及面积，但部分学生对于计算組合图形的周长和面积就存在一定困难，我们可以让学生画出图形，让图形来架起学生形象思维和抽象思维之间的桥梁。

如：把3个边长2分米的正方形拼成一个长方形，长方形的周长是多少分米，面积是多少平方分米？学生只要正确画出下面图形，标上数据，就能很快求出组合图形的周长和面积。

周长：（2+6）？=16（分米）

面积：6？=12（平方分米）

还有一个例子，前段时间在网上转的比较火的一道数学题目。

题目：在下面图形上添加一条线使其变成2个三角形。

答案是沿左上角向右下角画一条刚好盖住那个缺角的粗线，出现的就是2个三角形了。解决此题的据说是一个小学生，不是其难度大，而是数形结合思维的巧妙运用，所以数形结合思想的广泛运用也可以说明。数形结合思想的利用，有助于学生思维的开拓。

数学家阿蒂亚曾经说过：“代数是有序的逻辑，几何是看得见的逻辑，概率是无序的逻辑。”正因为几何是看得见的逻辑，因此利用几何模型可以使小学生更容易接受，在这一过程中，数形结合思想、空间观念的发展也能得到很好的体现。

在小学数学教学中，数形结合能为学生提供恰当的形象材料，可以把无形的解题思路形象化，将抽象的数量关系具体化，不仅有利于学生顺利、高效地学习数学知识，更有利于学生学习兴趣的培养、智力的开发、能力的增强，使教学收到事半功倍之效。最关键的一点，数形结合能使抽象枯燥的数学知识形象化、具体化，使得数学教学充满乐趣。相信巧妙地运用数形结合，一定会引导学生由怕数学变成爱数学。

参考文献

[1] 王舒瑶.数形结合思想在小学数学教学中的应用研究[D].重庆：西南大学，2015.

[2] 张晓明.浅谈数形结合思想在小学数学中的应用[J].学周刊，2014（33）.