基于模糊熵和模糊夏普比率的多阶段投资组合模型及实证

2019-06-09王中兴卢余刚

广西大学学报（自然科学版） 2019年6期

王中兴，卢余刚

(广西大学数学与信息科学学院, 广西南宁530004)

0 引言

平衡投资的收益和风险，确定各种资产的投资比例是投资组合研究的重要组成部分。MARKOWITZ[1]在1952年使用收益的方差来度量风险，建立了期望收益最大、风险最小的均值—方差投资组合模型。在此之后，许多学者开始关注投资组合的收益度量问题。例如SWALM[2]利用半方差衡量风险；KONNO[3]用绝对方差来度量风险等。以上学者从风险度量的角度提出了许多经典的投资组合模型，如均值—半方差投资组合选择模型，均值—绝对方差投资组合选择模型等。众所周知，高收益总是伴随着高风险，那么风险和收益如何抉择？1966年SHARPE[4]提出了Sharpe比率，Sharpe比率的定义为超出无风险收益的收益率与标准差的比值，衡量每个单位风险所获得的超额收益。随后，许多学者基于Sharpe比率提出了一系列的改进，例如SORTINO等[5]利用下侧风险替换Sharpe比率中的标准差。VINOD等[6]使用原始样本生成再生样本，进而提出“双重Sharpe比率”。ZAKAMOULINE等[7]提出了调整的Sharpe比率等。由于资产收益率存在模糊不确定性，2015年NGUYEN等[8]提出了模糊Sharpe比率，用模糊收益率代替传统Sharpe比率中清晰收益率。

在投资的过程中，由于市场影响因素比较复杂，资产的风险和收益率具有很强的不确定性。因此人们基于ZADEH[9]提出的模糊集概念以及LIU[10]提出的不确定理论来研究投资组合问题。例如ZHANG等[11]把投资组合收益看作模糊随机变量，建立了基于可能性均值方差的投资组合模型；王竟竟等[12]提出了具有交易量和交易成本约束的多期模糊投资组合模型。为了描述模糊变量的随机不确定性，LI等[13]定义了一种新的模糊熵，在此基础上BHATTACHARYYA等[14]等提出了一个新的投资组合模型，该模型使得均值和偏度最大化，方差和交叉熵最小化。DENG等[15]建立了带有交易成本的模糊投资组合模型，并分析了算法的灵敏度。另外由于投资者投资行为的长期性，研究多阶段投资组合问题也具有重要意义。MERTON[16]研究了连续时间下的多阶段投资组合问题，SADJADI[17]在假设借贷利率不相等的情况下，研究了模糊多阶段投资组合问题。

本文利用模糊熵度量投资收益的不确定性，模糊夏普比率衡量投资效率，以资产组合收益和投资效率最大、投资风险最小为决策目标，构建多阶段的多目标投资决策模型，并采用理想点法将模型转化为单目标优化模型并利用遗传算法进行求解。

1 可信性均值及模糊夏普比率

1.1 可信性均值和模糊熵相关概念

为了将模糊变量清晰化，文献[10]在模糊数的基础上提出了可能性测度和必要性测度，进而给出了模糊变量的可信性均值，可信性方差和模糊熵等概念。

(1)

(2)

(3)

即:

(4)

(5)

(6)

(7)

对于风险资产投资组合问题，文献[18]分别定义资产组合的可信性收益，可信性方差和模糊熵如下：

(8)

(9)

(10)

1.2 模糊夏普比率

(11)

(12)

其中Rb表示无风险资产收益率。

2 模糊多阶段投资组合模型

2.1 模型建立

(13)

第t期投资者的财富值Wt可以表示为：

(14)

其中t=1,2,…,T。通过对式(14)进行迭代，第h期(h=1,2,…,T)投资者拥有的总财富Wh可表示为：

(15)

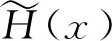
(16)

(17)

投资目标为最终财富价值最大化，并且使整个投资过程的累积夏普比率最大化，模糊熵最小，则建立基于模糊熵和模糊夏普比的多阶段投资组合模型如下:

(18)

模型(18)第一个约束要求各资产投资比例之和为1。第二约束代表投资比例上下界限制。可以看出，该模型的经济意义是指在上述两个约束条件下，投资者通过分配投资比例来最小化投资组合的风险，最大化投资效率，实现财富最大化。

2.2 模型求解

由于模型(18)为多目标投资组合模型，其最优解难以求出，通常做法是将多目标优化转换为单目标优化。本文利用理想点法进行转换，理想点法的基本思想是对于多目标规划问题：

(19)

先分别求出各个分目标函数φi(x)和φj(x)的最优值φi,max(x),(i=1,2,…,n)和φj,min(x),(j=1,2,…,m)，将这些由最优值构成的点称为理想点，然后根据实际点与理想点之间的距离构造评价函数和单目标优化问题：

(20)

即在多目标规划的可行域内，尽可能的“逼近”理想点。

利用上述理想点法将多目标规划化模型(18)转化为动态单目标规划模型：

(21)

3 实证研究

从上海证券交易所A股抽取了10支股票，这10支股票属于不同行业。数据选取的时间区间为2015年至2018年(数据收集自同花顺软件)，计算此区间的日收盘价，以一年为一个计算周期，使用文献[20]提出的频数统计法对数据进行处理，得到每支股票的三角模糊收益率，具体数据如表1。

表1 股票模糊收益率Tab.1 Stock fuzzy return rate

表2 股票最优投资比例及各期财富Tab.2 Optimal investment ratio of stocks and periodic wealth

由表2可以看出，基于模糊熵和模糊夏普比率的多阶段投资组合的模型最优解分布性较好，在第一期投资结束后投资和拥有12 096.45元，在第二期投资结束后，受市场大盘整体低迷的影响，其资产变为9 750.59元。在第三期投资结束后投资者扭亏为盈，总资产变为13 532.42元。从上述实证数据说明了该模型在中国证券市场下的实用性和有效性。

投资组合问题一直是许多学者研究的重点问题。本文在已有文献的基础上，利用模糊熵度量投资风险，模糊夏普比率衡量投资绩效，构建了多阶段投资组合模型。实证数据(表3～表5)表明基于该模型的投资决策可行、有效，投资者可以在实际投资中参考。