斜拉桥拉索损伤对主梁线形的影响分析

陶俊杰，王慧平，付兆茜

(1.湖州市城市规划设计研究院,浙江 湖州 313000；2.江西理工大学；3.建研凯勃建设工程咨询有限公司)

1 引言

斜拉桥在建成通车后，在长期荷载作用以及各种环境因素影响下，结构的性能逐渐发生变化。因此，把握桥梁在运营期间的结构特性非常重要。拉索是斜拉桥结构中最重要的构件，但是由于斜拉索长期承受疲劳荷载，又处于跨江河、跨海湾地域，长期暴露在风雨、潮湿和污染空气的环境中，易腐蚀，因此拉索也是斜拉桥结构最容易引起损伤的构件。研究斜拉桥拉索状态变化与全桥整体性能的联系，是建立斜拉桥监测系统和通过监测数据来评价桥梁整体性能的基础，对已建斜拉桥的拉索更换及日常维护可以提供指导性意见，同时，对于其他新建斜拉桥的拉索设计也具有一定的借鉴意义。

该文以某大桥实际监测数据为基础，采用优化设计原理建立能真实反映现有结构若干真实特性的基准有限元模型。在此基础上研究不同位置的拉索损伤和相同位置不同程度的拉索损伤对斜拉桥主梁线形的影响。找出对结构影响较明显的拉索以及拉索损伤对桥梁结构的影响规律，为评估大桥拉索的安全状态提供可靠的依据，也可为桥梁结构健康监测技术的开发与应用提供理论根据。

2 基于现场测试数据的基准有限元模型

由于材料的腐蚀老化、过载运营、疲劳、徐变等因素导致桥梁结构的静、动态特性都与刚竣工时的斜拉桥有较大的差别。要对斜拉桥的整体性能进行健康评估，就需要建立一个能真实反映现有斜拉桥特性的基准有限元模型。

斜拉桥有限元模型如图1所示。钢拉索的编号按南、北桥塔分别编定，北塔河侧索用“R”表示，北塔岸侧索用“B”表示，北塔上游侧的索用“U”表示，北塔下游侧的索用“D”表示，以最接近桥塔的最短索为1号索，最远离桥塔的索为11号索，南塔的编号规律与北塔相同，为了区别开，用相应的小写字母 “r”、“b”、“u”、“d”来表示。例如“RU6”表示北塔河侧上游6号索，“bd6”表示南塔岸侧下游6号索。图2为北塔各斜拉索的编号示意图。

图1 斜拉桥三维有限元模型

图2 北塔斜拉索编号示意图

采用优化理论建立斜拉桥基准有限元模型。模型建立的具体步骤如下：① 根据设计索力、设计弹性模量等设计资料，建立斜拉桥初始模型；② 通过计算获得有限元实际索力，并对索力进行循环迭代，使得有限元模型索力接近测试索力；③ 采用结构桥塔和索的弹性模量作为参数，采用有限元计算得到的主梁挠度与测试挠度差作为目标值，应用优化理论对初始有限元模型进行参数修正，使得目标值最小；④ 对索力进行循环迭代，反复此过程，最终形成基于现场挠度观测数据的基准有限元模型。表1为初始模型、基准模型和实测值部分测点挠度误差值对比。经验证，该模型能够正确反映现有结构的若干真实特性。该基准模型为索力变化影响下该桥的整体性能分析提供了分析平台，该建模方法也为可同类在役斜拉桥的研究提供参考依据。

表1 初始模型与基准模型部分测点挠度误差值对比

3 典型拉索损伤对主梁线形的影响

为了研究拉索损伤对主梁线形的影响，首先讨论不同斜拉索对称和非对称破断的情况，然后研究斜拉索在不同损伤程度下主梁线形的变化情况。对于该大桥，选取11号、9号、5号和2号索分别作为长索、中长索、中索和短索的典型代表进行研究。

3.1 典型拉索对称破断对主梁线形的影响

对称破断是指既对称于跨中又对称于桥轴线的拉索破断。表2为对称拉索破断工况以及对应的跨中挠度增量有限元计算结果。

图3、4分别为各工况下副跨和主跨主梁线形的变化情况。

从表2以及图3、4可以看出：长索与中长索破断对主梁线形的影响要大于较短索的影响；副跨背索、跨中拉索和中长索的对称破断对主梁线形的影响最大，主跨明显下沉。短索与中索的破断仅对自身锚固位置附近的主梁线形有少许的影响，而对整体线形影响较小。跨中挠度对主跨跨中拉索的敏感程度要强于对副跨拉索的敏感程度。

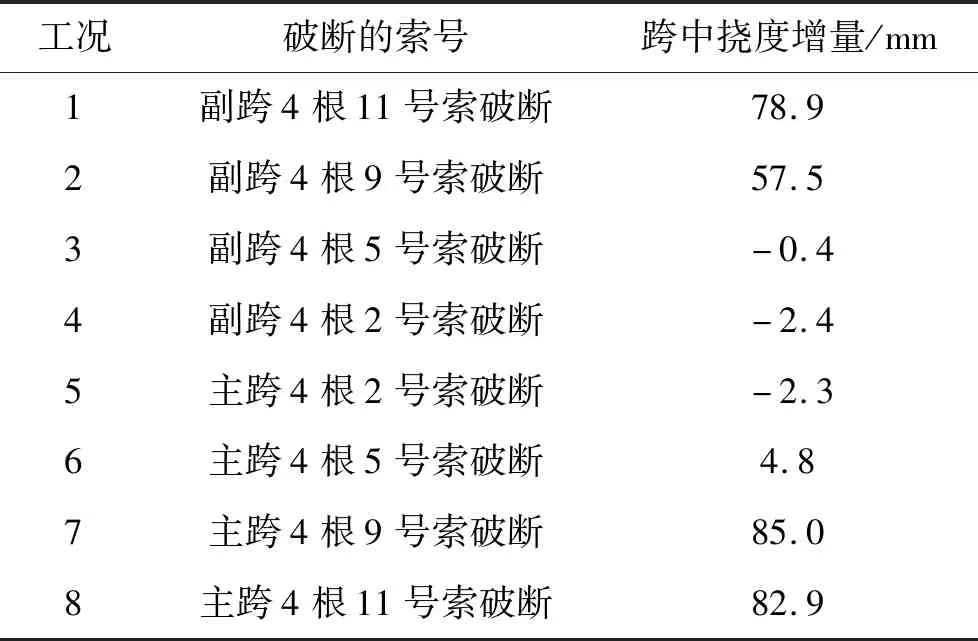
表2 破断工况与跨中挠度增量计算结果

3.2 典型拉索非对称破断对主梁线形的影响

由上述分析可知，长索与中长索对主梁线形的影响较大。此节通过分别对北塔的主跨和副跨11号索进行破断，研究两根拉索对称破断和单根拉索破断对主梁线形的影响。表3为各种工况和相应的跨中挠度的增量。图5、6为各种工况下的主梁线形。

图3 副跨拉索完全对称破断对主梁线形的影响

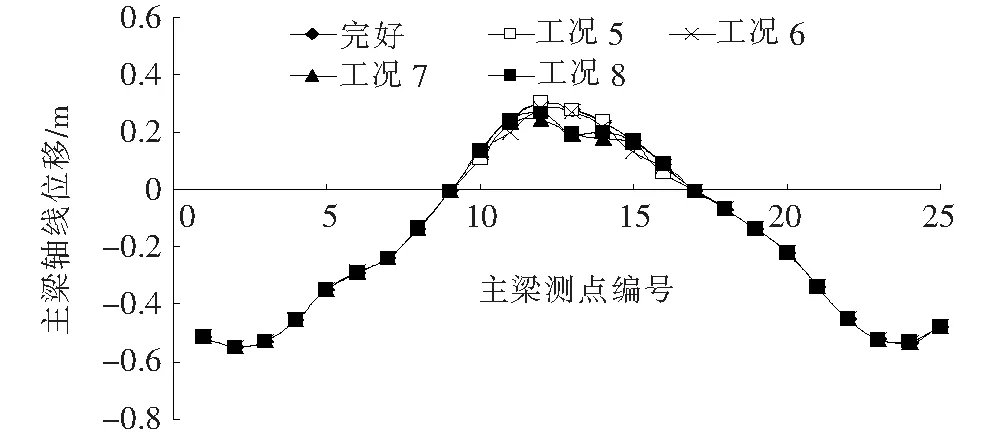
图4 主跨拉索完全对称破断对主梁线形的影响

表3 破断工况与跨中挠度增量

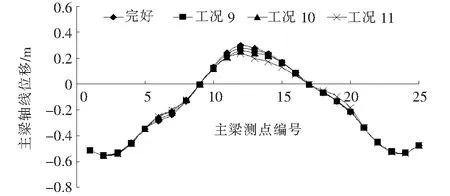
图5 北塔背索不对称破断对主梁线形的影响(副跨)

图6 北塔跨中拉索不对称破断对主梁线形的影响(主跨)

从表3及图5、6可以看出：4根拉索对称破断(工况11和14)对主梁线形的影响最大，对称于桥轴线的两根拉索破断(工况10和13)对主梁线形的影响次之，单根拉索破断(工况9和12)对主梁线形的影响最小。其次，非对称副跨背索的破断(工况9和10)使得跨中挠度增量的峰值偏向于破断索的一侧，非对称主跨跨中拉索的破断(工况12和13)使得跨中挠度增量的峰值偏向于破断索的对称侧。

3.3 典型拉索不同程度损伤对主梁线形的影响

(1)

(2)

(3)

损伤变量D可以表示为：

D=1-ψ

(4)

假设受损伤的材料在有效应力作用下产生的应变与无损伤时的应变等效，即应变等效原理。可得：

(5)

将式(3)、(4)代入式(5)中，可得：

(6)

(7)

这里选取损伤率为40%、60%、80%的情况进行研究，并且与完好工况(损伤率为零)及破断工况(损伤率为100%)相比较。表4为不同损伤程度的斜拉索的弹性模量。表5为各种损伤情况下相应的跨中挠度的增量。

图7为最外侧背索(B11)不同的损伤程度对主梁线形的影响，图8为跨中拉索(R11)的不同损伤程度对主梁轴线线形的影响。

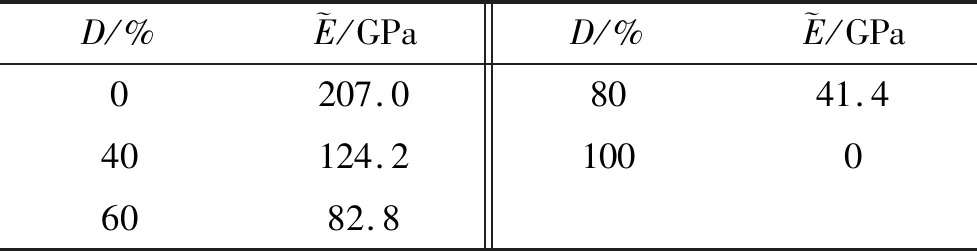
表4 不同损伤程度拉索的弹性模量

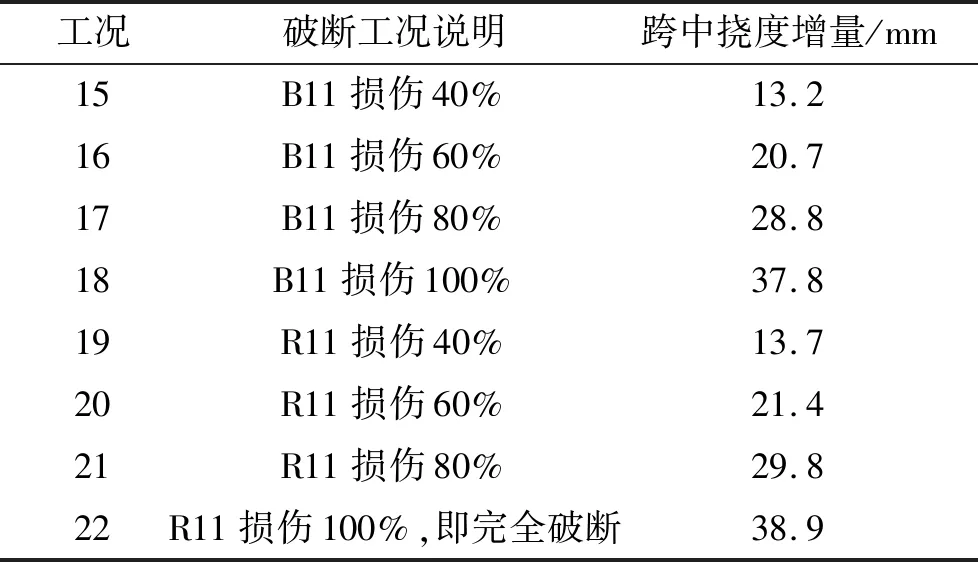
表5 不同损伤程度的跨中挠度增量

图7 B11的不同损伤程度对主梁线形的影响

图8 R11的不同损伤程度对主梁线形的影响

从表5和图7、8可以看出：在弹性工作范围内，相同拉索的损伤程度不同，对线形的影响趋势是相同的，仅表现为数值大小的区别；同时验证了前面的结论，副跨背索的损伤使得主跨跨中挠度增量峰值偏向于损伤索的一侧，主跨侧索的损伤使得主跨跨中挠度增量峰值偏向于损伤索的对称侧。

4 结论

通过能反映现有结构若干真实特性的基准有限元模型，研究了拉索损伤对斜拉桥结构主梁线形的影响，得出以下主要结论：

(1) 通过对不同位置的斜拉索损伤下桥梁的静力分析可知，背索和跨中拉索对全桥结构影响最大。

(2) 短索与中索的损伤仅对自身锚固位置附近的主梁线形有少许影响，而对整体线形影响较小。

(3) 副跨侧索的损伤使得主跨跨中挠度增量峰值偏向于损伤索的一侧，主跨侧索的损伤使得主跨跨中挠度增量峰值偏向于损伤索的对称侧。