基于时延估计法的泄漏噪声定位试验研究

刘志强　黄霄　廖伊丹　彭小兰　张建智　谢伟

摘   要：针对电站锅炉炉管泄漏问题，对基于时延估计法的定位方法进行了试验研究.通过外放高频声音信号模拟炉管泄漏信号，采用互相关算法估计两两通道间的时延值，根据距离公式建立定位方程，采用牛顿迭代法对其求解，获得泄漏点位置.试验结果表明：当声源为脉冲信号时，时延估计值很准确，当声源为连续周期声源信号时，时延估计值最大在-T/2～T/2（声源信号的周期）范围内变化;在一定范围内，采样率越高，时延值精度越高，定位效果越好;相较于声速，采样率对定位结果的影响更大.

关键词：锅炉炉管;声学检测;时延定位;采样率

中图分类号：TN91                      文献标志码：A

Investigation on Location of Leakage Noise Based

on Time Delay Estimation Method

LIU Zhiqiang1，HUANG Xiao1，LIAO Yidan1，PENG Xiaolan2，ZHANG Jianzhi1，XIE Wei1

（1. School of Energy Science and Engineering，Central South University，Changsha 410083，China;

2. Hunan Special Equipment Inspection & Testing Institute，Changsha 410111，China）

Abstract：Aiming at the leakage problem of boiler tubes in power plants，the location method based on time delay estimation was studied. The leakage signal of the furnace tube was simulated by the external high-frequency sound signal，and the multi group delay value was measured by the cross-correlation algorithm. The location equation was established according to the distance formula，and then solved by Newton iterative method，by which the leakage point coordinate was obtained. The experimental results show that the time-delay is effective only for impulsive sound source signals，and when it is the continuous periodic source，the estimation of time-delay is in the range of -T/2～T/2 （where T is the period of the source signal）. In a certain range，the higher sampling rate results in the higher delay value precision and the better effect of location;when compared with the sound speed，the sampling rate has greater impact on the location results.

Keywords：boiler tube;acoustic detection;localization of time delay;sampling rate

爐管泄漏是锅炉安全运行的重大隐患，因此，有必要对其进行及时有效的检测.常规的检测方法有：目测观察法、锤击检测法、声学检测法等[1-2].目测观察法和锤击检测法在我国中小型电厂应用得最早、最广泛，但是其主观因素强、准确率不高且不能提前预测，总体效果不佳.针对声学检测法的定位问题，各国学者进行了广泛而深入的研究，波束形成法[3-5]、高分辨率谱估计法[6-7]相继被提出，这些方法虽然具有较好的定位能力，但也受到算法复杂、传感器数量多、成本高、需要环境和噪声的先验知识、不适用实时系统等的限制.时延估计法[8-10]实时性好，算法简单，且能获得较高的定位精度.

本文将时延估计方法应用于炉管泄漏噪声的定位[11-13]中，首先分析时延估计方法的基本原理以及基本性质，并对互相关时延估计进行了理论推导.用信号发生器生成了频率3 000 Hz以上的高频信号模拟炉管泄漏信号，并在此基础上进行了大量声发射源定位试验，研究声源信号类型、采样率、声速等因素对定位结果的影响.

1   时延估计及定位原理

1.1   时延估计

声音传感器布置在锅炉表面的位置不同，泄漏声源到达各个声音传感器的时间也不一致，存在时延.利用此时延值，结合声音在锅炉内部的传播速度，即可推算出各个声音传感器的声程差，反推出声源位置，如图1所示.

互相关函数[14]表示的是两个时间序列之间的相关程度，即描述随机信号A（t）、B（t）在任意两个不同时刻t1、t2取值之间的相关程度.由于同源信号存在一定相关性，故通过计算不同声音传感器接收到的同源信号的相关函数，就能得到声源到达不同声音传感器之间的时间差.假设两个处于不同位置的声音传感器接收到的同源信号分别为A（t）和另一个延迟时间为τ的B（t+τ），它们的互相关函数可由式（1）给出：

式中：T为一个有限的时间间隔.

由式（1）可见，若τ是变化的，则互相关函数是τ的函数，RAB（τ）的特性可以通过将A（t）和B（t）分成n个小的相等时间段的积来观察.

令t = ti，A（t） = ai，B（t） = bi，i = 0，1，2，…，n若 B（t）相对于A（t）有一段时间延迟τ′，则：

式中：ai + j 和bi -  j 的下标随着RAB（τj）中τj的变化而变化.

互相关函数是在有限时间范围内积分.在实际应用中，数据采样仅利用了每个波的有限部分，而在被利用部分之外的波幅为0，即若i > n，则ai  = bi = 0;若j > 0且i + j > n，则ai+ j  = 0;若j < 0且i + j > n则bi- j  = 0因此，当j增加时，i + j增加，式（2）中的某些求和项将为0.随着j的增加，求和项数将越来越少，RAB（τj）的幅值逐渐下降.最终，当j > n所有的ai+ j 和bi- j项为0，RAB（τj） = 0.当τj = τ′时，由于A和B同相位，则RAB（τj′）达到最大值.因此，从RAB（τj）的最大峰值部位可以获得B（t）相对于A（t）的时差或时间延迟τ′.

1.2   声源定位模型

确定时延值只是进行声源定位的第一步，下一步将根据时延值与声音传感器阵列的几何关系定位声源.选取不同的声音传感器阵列几何结构，所对应的定位算法也各有差异.目前，基于时延（TDOA）的定位算法中广泛应用的有圆阵列、平面阵列、空间阵列[15-17].平面阵列实现较为简单，但存在定位识别死角.根据锅炉炉膛的形状以及空间限制，本文选择将4个声音传感器采用空间布置，组成一个有4个测点的空间阵列，并对定位算法进行了改进，取得了较好的性能.声音传感器阵列与泄漏声源的相对位置关系如图2所示.

建立空间直角坐标系，声音传感器的坐标分别为S0（x0，y0，z0）、S1（x1，y1，z1）、S2（x2，y2，z2）、S3（x3，y3，z3）.为简化计算，将声音传感器S0的坐标固定在坐标原点.S1、S2、S3声音传感器的坐标可以根据与S0的相对位置关系确定.假定声源A在空间直角坐标系中为点声源，坐标为（x，y，z），以球面的方式进行传播.根据两点之间的距离公式，声源A可以和声音传感器S0、S1、S2、S3联立，建立非线性方程组，简化得到式（3）：

式中：di为声源到传感器Si与到坐标原点的声程差（di = τi·ν），m;ri为传感器Si到坐标原点，也就是Si与S0的距离，m.

采用牛顿迭代法求解该非线性方程组.

2   试验装置

2.1   硬件系统

为验证物理模型以及数学算法的准确性和实用性，本文选择了相应的硬件、软件，搭建了试验装置，其系统示意图如图3所示.

声音传感器：采用自由场声音传感器，其型号为MPA426，频率响应为20～20 000 Hz，靈敏度为50 mV·Pa-1，动态范围为29～127 dBA.它测量到的是

消除了传声器对声场影响的声压，出厂前经过相

位[18-19]匹配.

数据采集卡：本文采用USB多通道数据采集卡，其型号为USB2881，输入量程为±5 V、±10 V，校准方式为软件自动校准.鉴于泄漏声源和背景噪声的声学特性，数据采集卡的采样率很高，可达250 kS·s-1，同时，考虑阵列声源定位中传感器阵列的需求，此数据采集卡可16路单端输入、12路差分

输入.

2.2   软件系统

本系统主要采用Matlab进行数据处理，可以实现锅炉炉膛声音信号的实时采集与存储、声学特性分析（包括滤波与频谱分析）、时延值估计和声源

定位.

2.3   试验装置误差分析

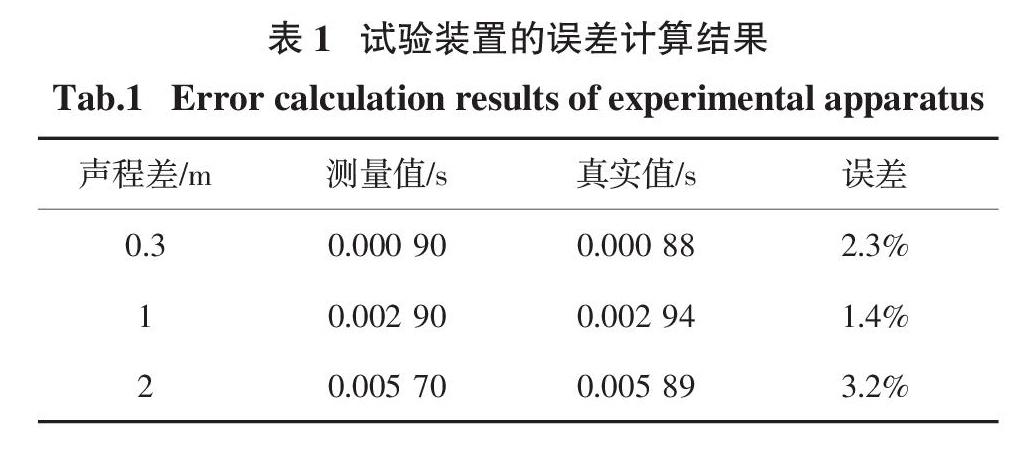
试验装置采用的仪器之间电气性能不一致，存在误差，如：传声器之间的相位差，数采卡各通道之间的相位差等.在一个长宽高分别为13 m×6 m×5 m的室内会议室开展试验装置性能测试，声源为模拟泄漏噪声信号，主频在2 000～3 000 Hz之间，由信号发生器生成、蓝牙音箱播放，各个声音传感器的摆放位置与声源保证在同一直线上，传感器的间距为0.3 m、1 m、2 m，系统采样率取f = 100 kHz，声速取v=340 m/s，通过将时延值的真实值（τ = d/v）与试验装置的测量值进行对比，计算出装置误差.通过测试结果可知，试验装置的误差在4%以内，满足试验要求.时延测量值与真实值比较如表1所示.

3   试验结果分析

3.1   声源信号试验

3.1.1   脉冲信号

图4（a）给出了由两个不同声音传感器接收到的同源脉冲信号的时域图.时域图给出了0～30 ms的采样时间段，两个声音传感器分别接收到的电压信号与时间的关系.图4（b）给出了由两个不同声音传感器接收到的同源脉冲信号的典型互相关函数.广义互相关（generalized cross correlation，GCC），是指以相关为基础和核心，研究各种形式的相关关系.从-30～30 ms的60 ms的时间间隔内作为τ的函数被绘出.当τ = 11 ms时，GCC的峰值最大.

将x1（t）、x2（t）两路函数的周期T设置为5 ms，使时延值τ以0.5 ms为步长从-1.5 ms变化到11.5 ms，共进行27组测试，对比互相关算法的估计值与理论值的偏差，结果如图5所示.当声源为脉冲信号时，由声源位置、传感器位置或其它因素引起的真实时延值变化，用互相关算法估计出的时延值都会随着理论值一起变化，结果准确.

3.1.2   连续周期信号

图6（a）给出了由两个不同声音传感器接收到的同源连续周期信号的时域图.时域图给出了0～3 ms的采样时间段，两个声音传感器分别接收到的电压信号与时间的关系.图6（b）给出了由两个不同声音传感器接收到的同源连续周期信号的典型互相关函数.GCC从-3～3 ms的6 ms的时间间隔作为τ的函数被绘出.当τ=0 ms时，GCC的峰值最大.

进一步，将x1（t）、x2（t）两路函数的周期T设置为5 ms，使时延值τ以0.5 ms为步长从-1.5 ms变化到11.5 ms，共进行27组测试，对比互相关算法的估计值与理论值的偏差，结果如图7所示.当两个传感器接收到的同源信号为连续周期信号时，时延估计值最大在-T/2～T/2范围内变化，针对此类情况，传感器两两之间的最大声程差不能超过λ/2.因此，在对连续周期信号进行定位时，需将阵列尺寸设置为λ/2以内.

3.2   采样率对时延值的影响

采样率的确定是一项重要的工作，只有正确选择采样率，才能保证获得最佳的性价比.若采样率过高，则被测量的精度高，但要求A/D转换器的转换速率快，数据量大，对处理器的数据处理速度和处理能力有更高的要求，相应地，系统成本也会增加;反之，若采样率过低，则会使采样结果无法恢复原始的模拟信号，造成测量结果的失真和出现

错误.

香农采样定理指出，只有采样频率大于原始信号频谱中最大频率的两倍，采样结果才能恢复原始信号的特征.因此，在选择采样率时，必须对被测信号进行分析，确定信号中最高次谐波频率，然后根据香农定理来确定采样频率;在确定最高次谐波频率（或截止频率）时，要求被测参量信号中去除了高于所确定的最高次谐波频率成分外，仍然应保留其主要特征，这样才不会造成测量精度的下降或测量信号的失真.实际使用中，采样率设置为输入信号最高频率的3～5倍.

试验所用声源的频率在2～3 kHz之间，为保证测量结果不失真，采样率的下限根据香农采样定理为10 kHz.目前大部分参考文献中，采样率参数的设置仅参考香农采样定理是不够的，因为声源定位对时延值的精度要求很高.通过试验测试发现，采样率设置为100 kHz，对应的时延值精度为1×10-5 s，定位结果的误差才会减小到系统误差以内（本文装置误差在4%以内）.因此，使采样率以10 kHz为步长从10 kHz变化到100 kHz，共进行10组测试，对比时延估计值与理论值的偏差，结果如表2、表3、表4所示.系统目前有4个传感器采集声源信息，因此，对应有3组时延值τ1、τ2、τ3.

综合分析表2、表3、表4的结果，在一定范围内，增大采样率，会降低时延值误差.尤其是采样率从10 kHz变化到50 kHz时，时延值的误差随着采样率的增大而显著减小，但是当采样率增大到50 kHz及以上时，时延值的误差虽然还在降低，但是降低的幅度没有之前明显.并且，提高采样率，会采集更多的环境声音信号，给滤波增加难度.綜合考虑，在进行声源定位试验时，将采样率设置为100 kHz.

3.3   采样率对定位结果的影响

基于互相关算法的声源定位通常分为2个步骤，首先利用互相关算法估计出时延值;接着利用估计出的时延值，计算声源的节点坐标.3.2节详细分析了采样率对时延值的影响，本节进一步分析采样率对声源定位结果的影响.

在室外空旷环境进行测试，声源特性与2.3节提及的保持一致.系统采样率仍以10 kHz为步长从10 kHz变化到100 kHz，共进行10组测试，采样时长为3 s，分析点数为2 048点.4个传感器坐标分别为S0（0，0，0）、 S1（0.5，0，0）、 S2（0，0.5，0）、 S3（0，0， 0.5），S0设为参考传感器.试验开始前，先根据式（4）计算当地声速.蓝牙音响在（2，0，0）处发声6次，测得相距0.5 m的0、1号传感器的平均时差为0.001 44 s，故当地声速为347.22 m/s（校准）.

式中：d为两传感器之间的距离，m;τ为两传感器之间的时延值，s.

采样率对声源定位结果的影响结果如表5所示.

表5的结果表明，在利用牛顿迭代法求解定位结果过程中，采样率越高，定位结果会越接近于声发射源的真实位置.为进一步获得采样率对定位结果的影响，可计算出不同采样率对应的定位结果的相对误差σ.定位结果的相对误差σ可根据式（5）进行计算.

式中：（x1，y1，z1）为定位结果;（x，y，z）为声发射源的坐标.

根据上式计算得出各种采样率试验对应的定位结果的相对误差σ，如图8所示.

从图8可以看出，采样率从10 kHz增大到100 kHz的过程中，定位结果的相对误差σ从整体变化趋势上来看，是变小的.表明随着采样率的增大，定位结果变得越来越准确.采样率从10 kHz增大到50 kHz时，定位结果的相对误差σ从23%左右减小到17%左右;采样率从50 kHz增大到100 kHz时，定位结果的误差σ从17%左右减小到5%左右.提高采样率，对提高定位结果的精度有显著作用.所以无论是采购硬件设备、搭建试验装置、还是改善算法，采样率都应被慎重考虑.

3.4   声速对定位结果的影响

基于时延估计法的定位问题需要确切可知的声源传播速度信息，传播速度的极小误差都会极大地恶化泄漏信号的定位精度.但在很多实际应用中，声源传播的速度信息并不可知，例如炉管泄漏信号在炉膛中传播.这种情况下，定位结果需将声源传播的速度考虑进来，以提升定位精度.声音在空气中传播时，速度会受温度的影响.根据声学理论可知，对于空气，声波的传播速度为：

ct = 331.6 + 0.6 t         （6）

式中：ct为声波的传播速度，m/s;t为声波所处环境的温度，℃.

当温度误差控制在±2.5 ℃范围内时，由此引入的声速误差为0.6×2.5=1.5.当天实验的环境温度为15 ℃，声速在（340±1.5）m/s变化，对定位结果的影响如图9所示.

图9结果表明：1）声速对定位结果的影响是线性的，正相关的.在其它影响因素保持不变的前提下，计算的声速偏大，会造成定位结果偏大;计算的声速偏小，会造成定位结果偏小.2）声速在（340±1.5） m/s（0～0.44%的误差范围）变化，x方向的定位误差在2.78%～5.73%之间，y方向的定位误差在0.003 9～0.037 6 m之间，z方向的定位误差在0.58%～8.00%之间，对定位结果的影响很大.3）一般环境中，声速只受温度影响，很好确定.但是在锅炉炉膛等复杂环境中，声速不仅受温度、湿度、压力等因素的影响，还牵涉到折射、反射，声速如何确定，应当进一步深入研究.

4   结   论

通过试验研究分析了影响声源定位系统精度的各种因素，并给出了相应的试验结果，提出了减小误差的方法和途径.这些试验结果和结论为提高声源定位精度，提供了依据.

对不同类型的声源进行时延估计，互相关算法表现出了不同的性能：针对脉冲信号，时延估计值与理论值吻合较好;针对连续周期信号，时延估计值最大在-T/2～T/2范围内变化.

分析定位结果随采样率的变化规律：采样率从10 kHz变化到100 kHz过程中，随着采样率的提高，时延值误差会显著降低，因而定位结果变得越来越准确，越来越接近声发射源的真实位置.

确定了采样率、声速对定位结果准确度的影响程度：采样率对定位结果准确度的影响最明显，而声速在（340±1.5）m/s范围内变化时，对定位结果准确度的影响也很大，但没有采样率的影响显著.

参考文献

[1]   姜根山. 锅炉管道泄漏声行为特性研究[J]. 华北电力大学学报，2006，22（3）：1—3.

JIANG G S. Study on acoustic behavior of boiler pipeline leakage [J]. Journal of North China Electric Power University，2006，22（3）：1—3. （In Chinese）

[2]   安连锁，冯强，沈国清，等. 电站锅炉管阵列内声传播特性及时延值测量[J]. 动力工程学报，2017，37（1）：13—17.

AN L S，FENG Q，SHEN G Q，et al. Acoustic propagation characteristics and time delay measurement in power plant boiler tube array [J]. Journal of Chinese Society of Power Engineering，2017，37（1）：13—17. （In Chinese）

[3]   杨洋，褚志刚，倪计民，等. 除自谱的互谱矩阵波束形成的噪声源识别技术[J]. 噪声与振动控制，2011，31（4）：145—148.

YANG Y，CHU Z G，NI J M，et al. Research on algorithm of sound source identification based on cross-spectral beamforming with exclusion of auto-spectrum [J]. Noise and Vibration Control，2011，31（4）：145—148. （In Chinese）

[4]   褚志剛，杨洋. 近场波束形成声源识别的改进算法[J]. 农业工程学报，2011，27（12）：178—183.

CHU Z G，YANG Y. Improved algorithm of near-field beamforming for sound source identification [J]. Transactions of the Chinese Society of Agricultural Engineering， 2011， 27（12）： 178—183. （In Chinese）

[5]  MICHEL U. History of acoustic beamforming [C]// 1th Berlin Beamforming Conference. Berlin：DLR，2006：21—22.

[6]   刘志刚，李录明，赵冬梅. 现代谱估计法及应用效果[J]. 石油地球物理勘探，2009，26（1）：5—9.

LIU Z G，LI L M，ZHAO D M，Modern spectrum estimation method and its application effect [J]. Oil Geophysical Prospecting，2009，26（1）：5—9. （In Chinese）

[7]   CAMPBELL W，SWINGLER D N. Frequency estimation performance of several weighted Burg algorithms [J]. IEEE Transactions on Signal Processing，2002，41（3）：1237—1247.

[8]   CHEN J，BENESTY J，HUANG Y. Performance of GCC- and AMDF-based time-delay estimation in practical reverberant environments [J]. Eurasip Journal on Advances in Signal Processing，2005，25（1）：960—964.

[9]   王宏禹，邱天爽. 自适应噪声抵消和时间延迟估计[J].大连理工学报，1999，35（3）：17—20.

WANG H Y，QIU T S. Adaptive noise cancellation and time delay estimation [J]. Journal of Dalian University of Technology，1999，35（3）：17—20. （In Chinese）

[10] YI H，WU C N. A new moving sound source localization method based on the time difference of Arrival [C]// 2010 International Conference on Image Analysis and Signal Processing. New York：IEEE，2010：118—122.

[11] 郭俊成. 基于传声器阵列的声源定位技术研究[D]. 南京：南京航空航天大学民航学院，2007：28—32.

GUO J C. Research on acoustic source localization technology based on microphone array [D].Nanjing：College of Civil Aviation，Nanjing University of Aeronautics and Astronautics，2007：28—32. （In Chinese）

[12] 王琳，姜根山，安连锁，等. 炉内管道泄漏声检测与定位系统的研究现状[J]. 华东电力，2009，29（6）：8—10.

WANG L，JIANG G S，AN L S，et al. Research status of acoustic detection and location system for pipeline leakage in furnace [J].East China Electric Power，2009，29（6）：8—10. （In Chinese）

[13] MUNGAMURU B，AARABI P. Enhanced sound localization [J]. IEEE Transactions on Systems Man & Cybernetics Part B Cybernetics A Publication of the IEEE Systems Man & Cybernetics Society，2004，34（3）：1526—1540.

[14] LUU G T，RAVIER P，BUTTELLI O. The generalized correlation methods for estimation of time delay with application to electromyography[C]// Proceedings of the 4th International Symposium on Applied Sciences in Biomedical and Communication Technologies Barcelona. Spain：International Sustainable Energy Planning and Management. 2011：30—36.

[15] BENESTY J，CHEN J，HUANG Y. Microphone array signal processing [J]. Journal of the Acoustical Society of America，2003，125（6）：4097—4098.

[16] SONG K T，CHEN J L. Sound direction recognition using a condenser microphone array[C]// Proceedings of IEEE International Symposium on Computational Intelligence in Robotics and Automation. New York：IEEE，2003：1445—1450.

[17] JIANG W，CAI Z，LUO M，et al. A simple microphone array for source direction and distance estimation[C]//Proceedings of 2011 6th IEEE Conference on Industrial Electronics and Applications. New York：IEEE，2011：1217—1225.

[18] 吳静，赵伟. 适用于非同步采样的相位差准确测量方法[J]. 电网技术，2006，30（7）：73—76.

WU J，ZHAO W. Accurate Phase difference measurement method for asynchronous sampling [J]. Power System Technology，2006，30（7）：73—76. （In Chinese）

[19] 李建民，赵鹏，侯文，等. 基于相关理论的相位差算法的误差研究[J]. 中北大学学报（自然科学版），2009，30（6）：616—619.

LI J M，ZHAO P，HOU W，et al. Error study of phase difference algorithms based on relevant theory[J]. Journal of North University of China（Natural Sciences Editon），2009，30（6）：616—619. （In Chinese）