一种GMMHMM隐状态与高斯混合成份初始化算法
2019-06-07张军超蒋强荣
张军超 蒋强荣


摘 要:为了解决传统隐马尔可夫模型应用通常将隐状态数和混合成份数看作一致的弊端,更客观地描述问题,使模型研究适合现实的数据分布,参数设定更为精准,从而使算法效果达到最优,提出一种基于高斯混合分布、聚类思想和OEHS准则的适应数据分布且自动确定参数的算法。因隐马尔可夫学习算法由EM算法实现,但EM是局部最优算法,严重依赖初始值,从跳出局部最优的角度出发,对两个参数进行初始设定。与传统的随机初始化方法进行比较,实验结果表明,该算法能得到更好的结果。
关键词:隐马尔可夫模型;GMM混合成份;隐状态;自适应
DOI:10. 11907/rjdk. 181494
中图分类号:TP312文献标识码:A文章编号:1672-7800(2019)001-0081-05
Abstract:In order to solve the problem that in traditional application of hidden Markov model, the number of hidden states and the number of mixed components are usually regarded as the same, and to describe the problem more objectively so that the model research can be very suitable for the actual data distribution, and the parameters are set more accurately to make the algorithm achieve the best results, an algorithm based on Gaussian mixture distribution, clustering idea and OEHS criterion is proposed. At the same time, the hidden Markov learning algorithm is implemented by EM algorithm, but EM is a local optimal algorithm, which depends heavily on the initial value. From the point of jumping out of local optimum, so that the initial setting of the two parameters is conducted, which can adapt to the data distribution and automatically determine the parameters. Compared with the traditional random initialization method, the experimental results show that the proposed algorithm can get better results.
0 引言
20世紀60年代,鲍姆提出了隐马尔科夫模型(Hidden Markov Model,HMM),在语音识别领域使用,被广大科研人员熟知。文艺复兴科技公司是国际著名投资机构,因从1989年开始保持超高年回报率被业界誉为最高效的对冲基金,通过独特的数学模型,捕捉市场机会进行量化投资,而隐马尔科夫模型是主要工具之一[1]。可以看到,HMM在各个领域都有应用,具有广泛影响。常用的HMM模型可以根据观测状态分为两个类别:连续型和离散型。例如,连续型的GaussianHMM、GMMHMM,离散观测状态的有MultinomialHMM。
离散型模型使用较为基础,有几个重要的参数需要设置,例如:“startprob_”表示隐状态的初始分布概率,“transmat_”表示不同状态间的转移概率,“emissionprob_”表示观测值的发射概率矩阵。许博等[2]为了实时、准确地识别多种P2P应用流,提出采用离散型HMM的P2P 流识别技术,能减少模型建立时间,提高识别未知流的实时性和准确性,并能较好地适应网络环境变化。陈世文[3]针对微观的具体攻击特征检测问题,提出一种基于多特征并行隐马尔科夫模型,用HMM隐状态序列与特征观测序列的对应关系,将攻击引起的多维特征异常变化转化为离散型随机变量,实验结果表明,基于MFP-HMM(Multi-Feature Parallel Hidden Markov Model)的方法优于标准HMM等机器学习方法。
对于连续型观测状态的HMM模型,GaussianHMM是其主要实现,该模型假设观测数据按照高斯函数分布,存在与离散HMM相同的几个重要参数:Startprob、transmat和emissionprob,含义也一致,但是emissionprob成份不是以概率矩阵分布形式存在,而各个隐状态对应的观测值分布以单个高斯函数拟合实现概率密度函数。吴漫君[4]以隐状态为股价未来走势、观察值为股价指标,对相同数据进行分析,连续隐马尔科夫模型的实证结果优于离散模型。柳姣姣等[5]提出了一种基于时空密度聚类的连续型马尔科夫模型对时空序列进行预测的方法,针对如何有效预测不同尺度分布的时空序列问题,采用该模型对药品冷藏库中的时空序列温度数据进行分析预测,结果显示与其它预测模型比较,该方法更准确有效。
另外还有一种重要的连续型HMM模型即GMMHMM,不同于GaussianHMM,对emissionprob的实现是由几个不同高斯函数混合而成的,用来拟合发射概率函数。较前两者,GMMHMM更符合现实情况,对真实问题的解释更强,同时也更复杂。王慎波等[6]针对传统混合高斯模型(GMM)对运动目标检测方法计算量大、时间复杂度高的缺点,提出一种利用块模型的混合高斯模型运动目标检测方法,该算法平均耗时减少了46.16%,存储空间减少不低于54.15%。王慧勇[7]基于GMM-HMM系统模型更好地解决了多口音问题中模型不匹配以及特定口音数据稀疏导致的建模难题,进而提高了识别率。在此基础上,结合目前广州、重庆地区数据,实验表明:本文改进系统所带来的相对CER下降分别为23.03%和21.21%,性能提升效果相当明显。
1 关键算法理论
1.1 HMM算法
隐马尔可夫模型(HMM)是统计模型,是在探究一个马尔可夫过程与背后隐藏状态关系过程中建立的模型,用来描述一个含有隐含未知参数的马尔可夫过程[8]。HMM常用来从可观测序列中确定该序列隐含的参数,然后利用参数进一步研究分析[9-10]。
HMM根据使用背景不同分为离散型和连续型,典型的离散型是隐状态和观测值概率一一对应,而连续型HMM的隐状态和观测值概率通过隐状态的概率分布得到。隐马尔科夫模型通过三元组表示[(π,A,B)],完整表示为[(N,M,π,A,B)]。其中:N为隐状态数,M为一个隐状态对应的观测值数,[π]指隐状态的初始概率分布。
1.2 K-means理论
K-means算法对于不同初始值,可能会导致不同结果。解决方法是多设置一些不同初值,对比最后的运算结果,一直到结果趋于稳定结束。但是,很多时候事先并不知道给定数据集应该分成多少个类别才最合适。
K-means算法理论是对给定一个包含N个元素的数据集,且将其分为K个数据簇。基本过程是通过给定几个不同的数据簇中心,通过不断将数据归属簇且重新计算簇中心,尽可能达到簇间距最大而簇内距离最小的状态。
具体K-means算法[11]:对于给定的具有N个元素的数据集[X={x1,x2,?,xN},xi={xi1,xi2,?,xim}]表示一个数据项,m代表一个数据项维度。
K-means基本步骤:
(1)初始化。首先需要指定K参数的值,随机给定K个不同点作为初始K个簇的中心点。
(2)计算数据归属。遍历数据集X,同时计算每个数据项到K个簇中心的距离,并将其归属到距离最小的簇中,得到K个簇。
(3)更新簇中心。对K个簇的中心重新计算,通过新簇的数据求得平均值作为新的中心。
(4)重复步骤(2)、步骤(3)。当每个簇的中心不再变化时结束算法。
近年来有一些学者使用K-means聚类方法设定隐状态数目[12],但是K-means聚类算法对初始值太敏感,不同初始值会得到不同结果,而且需要事先设定k值。本文仅将K-means算法作为算法初始化参数的设置方法,可以粗略分类作为GMM的混合成份,同时减少候选成份,避免每个数据单独作为成份,大大减少了程序运行时间。
1.3 GMM理论
高斯混合模型在单高斯密度分布函数基础上发展而来,因GMM具有单高斯分布无法比拟的先天优势,可以用GMM描述训练数据样本的概率分布,对一些连续型概率分布問题具有很好的适用性,因此可以与HMM联合使用,克服HMM在解决连续性问题上的弊端,用GMM拟合HMM的发射概率,形成GMM-HMM算法[13]。描述为连续性观测值的概率分布使用混合高斯函数近似拟合。
一般机器学习参数求解步骤是先求得优化目标函数,然后对函数求导,使函数取到最优值,再令模型参数为此时的对应参数,但是对混合高斯的目标函数应用此法求解困难,不好求偏导。而EM算法也是一种求解最优值的优秀算法,可以使用EM求解GMM问题 [14]:首先,初始化GMM各参数;其次,基于该参数求得估计参数,使估计函数求到最大值,不断迭代这个过程,直到收敛。具体如下:
2 性能评价标准
2.1 准确率
目前机器学习领域使用的聚类性能评价指标有很多种[15]。本文采用准确率、纯度作为聚类实验工具,分析评价算法聚类性能。准确率公式如下:
在式(12)中,N代表实验的数据集大小;TP代表本属同一类别的数据项通过算法聚类仍划分为同一种簇的数据数目;FN代表不同类别数据项通过算法聚类仍划分为不同种簇的数据数目;Prec是准确率,代表在本数据集实验结果中,正确划分数据数目占到总数据数目的比例,该值越大说明实验结果越好,算法性能越高。
2.2 纯度
purity是另外一种常用的聚类评价指标,主要思想是统计正确聚类的数据数目占数据集的比例[16]。表示为:
其中,[Ω={ω1,ω2,?,ωk}]表示簇集;[ωk]表示第k个簇集;[C={c1,c2,?,cj}]是所有类集,[cj]指第j个类集;N是数据集大小。
Purity指标计算方便,值的范围为0~1,越大表示聚类错误的数据项越少。但是这个指标不能很好地适用退化聚类情况,即如果所有数据项单个成簇,仍然可以得到Purity的值为1。
2.3 OEHS准则
参数生成算法的评价方法采用OEHS准则,利用交叉检验似然值作为最终隐状态确定准则[17-18]。对于隐马尔科夫模型来说,隐状态N确定后,通过HMM计算序列隐状态的似然值,再进行HMM 隐状态标记。通过解码数据序列,得到隐状态数与序列似然值的关系,不同隐状态会有不同效果,以交叉检验似然值的 OEHS标准评价。但是模型会随着隐状态数增加而越来越复杂,最稳定合适的HMM隐状态数OEHS最小时的值。
首先设定一个数值范围,假设最优值在该范围内,依次遍历每个取值,计算每个取值的OEHS值,最后找到最小的OEHS值即为最优值。
3 KGO算法参数设定
传统观念认为HMM的隐状态数目在一定意义上也是一种数据分类结果,而数据分布是由若干种单高斯分布混合而成的,每一个高斯分布对应一个类别,因此可以用隐状态数目作为混合高斯的成份数,两者之间是一对一、相互转化并保持一致性的。但是如此粗略划分对认识问题本质进而解决问题都不是好方法。
传统做法是使用K-means作为确定隐状态数的方法[19],该方法有严重弊端:其一,需要大量遍历计算才能找到最优值,浪费了大量时间,效率很低;其二,需要事前指定取K值,过于主观随机,没有尊重数据本身的特点[20]。本文提出的算法可以解决该问题:第一,具有自适应性的算法,实现了根据数据特点设定隐状态数;第二,同时计算得出样本数据混合高斯的成份数;第三,不用事先指定隐状态数目,一次遍历数据,减少运行计算时间,大大提高了效率。
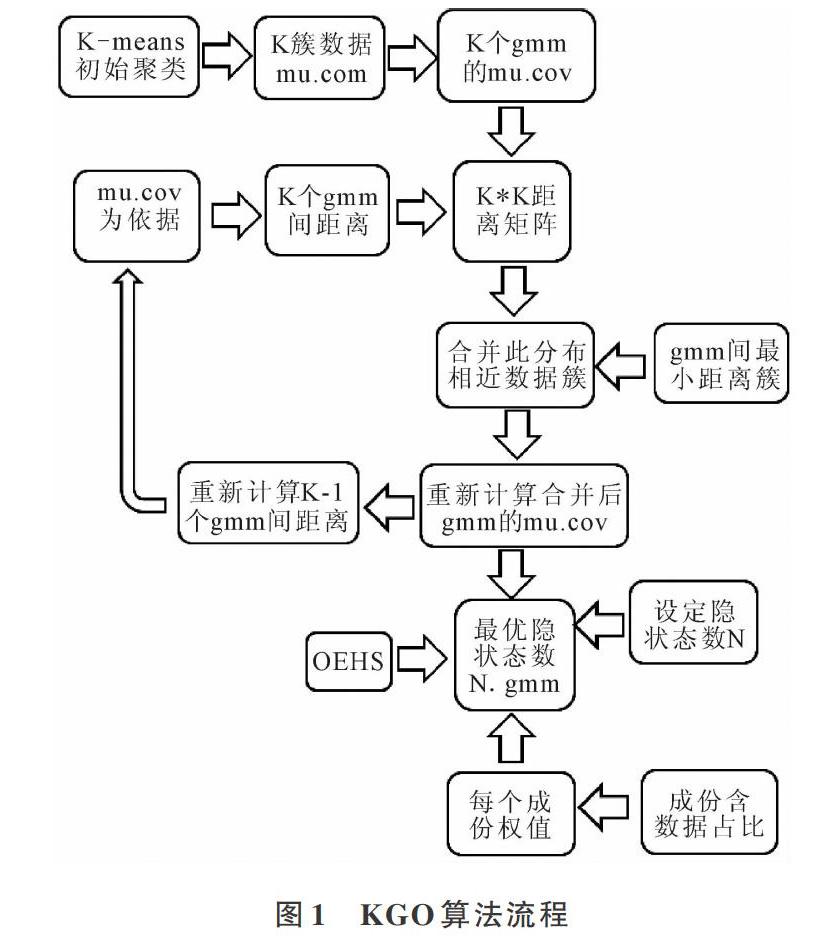
为了得到更好的预测结果,且更好地符合客观事实,分别对隐状态数目和单一隐状态对应数据混合高斯成份进行学习,结合多种算法,提出一种具有自主学习能力且对数据分布形状友好的算法:KGO算法。流程如图1所示。
KGO具体算法:
(1)以K-means聚类算法得到K个数据簇。
(2)计算K个数据簇的均值、协方差,分别作为初始K个GMM的参数:mu、cov。
(3)通过mu、cov计算GMM成份间的距离,得矩阵M。
(4)遍历M矩阵,得到间距最小的两个GMM成份,合并两个数据簇。
(5)重新计算本成份的mu、cov,同时更新M矩阵。
(6)以本次合并GMM成份和上次合并GMM成份所得到的M矩阵最小值间差值最大者作为最优候选GMM0。标榜合并已经到达最优,各个GMM成份间距离最大。
(7)以OEHS为准则,选取不同GMM-HMM的隐状态数,同时以GMM0为初始混合高斯成份。寻找最优隐状态数目N和每个隐状态对应的GMM。
4 实验结果
本文实验数据由两部分构成:一部分选取UCI数据挖掘数据库中的标准数据集4k2_far和Iris[21],另外一部分来自随机生成的不同维度数据集。各数据集详细情况如表1所示,实验仿真硬件环境:Intel 2.6GHz,内存8GB;操作系统:Microsoft Windows 10。
5 结语
本文同时利用K-means和聚类思想,对数据集4k2-far、Iris、5、3、2进行聚类测试,利用准确率和纯度作为评价标准,通过对不同情况数据集的仿真验证,可以得到清晰的性能对比,本文聚类算法可以不指定聚类个数,自适应数据分布情况,自动聚类出数据簇。基于此新算法的研究结果,进一步应用于混合高斯—隐马尔科夫模型,鉴于混合高斯-隐马尔科夫模型适用性能比较依赖参数初始化,对初始化要求较高,为了更好地适应数据分布,该模型可以根据数据情况,初始化混合高斯—隐马尔科夫模型的隐状态数目以及每个隐状态下混合高斯成份的参数。通过对股票数据的验证测试,本文提出的聚类算法可以很好地在不知数据分布情况时自动适应学习数据分布,设定混合高斯-隐马尔科夫模型的隐状态数目以及每个隐状态下混合高斯成份的参数,同时通过减少寻优时遍历数据的次数,大大提高运行效率,对模型效果有重要影响,同时对进一步优化模型性能有重要指导意义。
参考文献:
[1] 文芳. 股票量化策略:科学爱好者的游戏[J]. 新财富,2016(8):60-64.
[2] 许博, 陈鸣, 魏祥麟. 基于隐马尔科夫模型的P2P流识别技术[J]. 通信学报,2012,33(6):55-63.
[3] 陈世文. 基于谱分析与统计机器学习的DDoS攻击检测技术研究[D]. 郑州:解放军信息工程大学,2013.
[4] 吴漫君. 基于隐马尔科夫模型的股价走势预测[D]. 广州:华南理工大学,2011.
[5] 柳姣姣,禹素萍,吴波,等. 基于隐马尔科夫模型的时空序列预测方法[J]. 微型机与应用,2016,35(1):74-76.
[6] 王慎波,张为. 基于块模型的混合高斯模型运动目标检测方法[J]. 信息技术,2016(6):151-156.
[7] 王慧勇. 基于神经网络的多方言口音汉语语音识别系统研究[D]. 深圳:中国科学院深圳先进技术研究院,2014.
[8] 杜世平. 隐马尔可夫模型的原理及其应用[D]. 成都:四川大学, 2004.
[9] BAUM L E, PETRIE T, SOULES G, et al. A maximization technique occurring in the statistical analysis of probabilistic functions of Markov chains[J]. Annals of Mathematical Statistics,1970,41(1):164-171.
[10] BAUM L E,PETRIE T. Statistical inference for probabilistic functions of finite state Markov chains[J]. Annals of Mathematical Statistics, 1966, 37(6):1554-1563.
[11] 张素洁, 赵怀慈. 最优聚类个数和初始聚类中心点选取算法研究[J]. 计算机应用研究,2017,34(6):1617-1620.
[12] HU L, ZANIBBI R. HMM-based recognition of online handwritten mathematical symbols using segmental K-means initialization and a modified pen-up/down feature[C]. Asian Conference on Computer Vision,2011:457-462.
[13] ZIMMERMANN M,GHAZI M M,EKENEL H K,et al. Visual speech recognition using PCA networks and LSTMs in a tandem GMM-HMM system[C]. Asian Conference on Computer Vision, 2016:264-276.
[14] VERBEEK J J, VLASSIS N, KR?SE B. Efficient greedy learning of Gaussian mixture models[J]. Neural Computation, 2014,15(2):469-485.
[15] 冯柳伟,常冬霞,邓勇,等. 最近最远得分的聚类性能评价指标[J]. 智能系统学报,2017,12(1):67-74.
[16] 谭颖. 文本挖掘中的聚类算法研究[D]. 长春:吉林大学, 2009.
[17] CELEUX G,DURAND J B. Selecting hidden Markov model state number with cross-validated likelihood[J]. Computational Statistics,2008,23(4):541-564.
[18] 段江娇. 基于模型的时间序列数据挖掘[D]. 上海:复旦大学, 2008.
[19] 吴静,吴晓燕,滕江川,等. 基于连续隐马尔可夫模型的仿真模型验证[J]. 兵工学报,2012,32(3):367-372.
[20] 冯波,郝文宁,陈刚,等. K-means算法初始聚类中心选择的优化[J]. 计算机工程与应用,2013,49(14):182-185.
[21] 谢庆华,张宁蓉,宋以胜,等. 聚类数据挖掘可视化模型方法与技术[J]. 解放军理工大学学报:自然科学版, 2015(1):7-15.
[22] 贾瑞玉,宋建林. 基于聚类中心优化的k-means最佳聚类数确定方法[J]. 微电子学与计算機,2016,33(5):62-66.
(责任编辑:何 丽)
