基于多边形导航网格地图的改进A*算法
2019-06-07朱昌龙刘黎志
朱昌龙 刘黎志

摘 要:针对A*寻路算法在大型地图中搜索路径结点过多、搜索效率过低的问题,提出一种基于多边形导航网格的改进A*算法。首先利用建模工具对地图中障碍物进行剔除,生成可行走域的多边形导航网格;其次对多边形网格进行Delaunay三角剖分,形成三角导航网格,利用二叉堆对A*算法所使用的数据结构进行优化,采用目标范围界限方法对导航网格进行预处理,并将处理A*算法的启发函数进行改进以适用于多边形导航网格,对多边形导航网格生成路径利用漏斗算法进行路径平滑处理,生成实际最优路径;最后利用Unity3d游戏引擎搭建地图寻路实验平台,对比分析算法的性能差距。实验证明,基于多边形导航网格改进A*算法在大型地图中的搜索效率明显高于基于传统方格地图A*算法。
关键词:A*算法;Delaunay三角;多边形导航网格;平滑路径;漏斗算法
DOI:10. 11907/rjdk. 181825
中图分类号:TP301文献标识码:A文章编号:1672-7800(2019)001-0017-05
Abstract: Regarding the A-Star algorithm shortcomings of excessive searching nodes of path and inefficiency of searching in large tradition grid map,this paper propose an improved A-Star algorithm based on polygon navigation mesh map. Firstly, the obstacles are eliminated by using the modeling tool in the map to generate a polygonal navigation mesh for the walking domain. Secondly, a triangular navigation mesh is generating by using Delaunay triangulation on polygonal meshes, the data structure of A-Star algorithm is optimized by a binary heap,and the navigation mesh is precompted by goal bounding method and then the heuristic function of the A-Star algorithm is modified to apply to the polygonal navigation mesh, and then the path generated by the polygon navigation mesh is smoothed by funnel algorithm to generate the actual optimal path. Finally, building map-finding path comparative experimental platform is buitt by using the Unity3d game engine to compare analysis the performance gap of the algorithm. Experiments show that the search efficiency of improved A-Star algorithm based on polygon navigation mesh is significantly higher than that based on the traditional grid map A-Star algorithm in large maps.
Key Words: A-Star;Delaunay triangulation; polygon navigation mesh; smoothing path; funnel algorithm
0 引言
路径搜索一直是人工智能领域研究的热点,高效性和真实性一直是判断寻路算法性能的指标[1-3]。在人工智能路径搜索方面,运用最多的是A*算法[4]。相关领域研究者在A*算法基础上,进行了寻路算法的优化和改进,提高了寻路算法的性能。例如Daniel Harabor[5]提出JPS算法,利用跳点搜索的方法解决了传统等价方格地图中存在的对称性搜索结点问题,从而提高了搜索效率。但是目前大多数A*算法优化都是基于具有对称性的方格地图进行的,方格地图在大型地图中寻路网格结点较多,占用系统资源过多,从而导致搜索效率过慢。对此,本文提出基于多边形导航网格地图的改进A*算法,在A*算法搜索结点的数据结构上采用二叉堆技术,在地图预处理上运用一种目标范围界限的方法对地图进行信息划分,从而有效提高基于多边形导航网格A*算法的搜索效率[6-13]。
寻路地图也可以看作是一组存储地图信息的数据结构[14-16]。在运用寻路算法之前,需要先将地图进行预处理,地图划分方法有方格栅格法和导航网格法。
方格栅格法是将地图等距离划分为面积大小相同的网格,根据障碍物占网格面积的百分比确定是否为障碍物,使用遍历方法对地图中的信息进行预处理。利用方格栅格法预处理地图是一种简单的划分方法,划分地图占用内存较小、适用性较高,但运用到寻路算法时,所搜索的邻居结点和无用結点过多,导致搜索效率过低。
导航网格法是建立在多边形网格地图基础上的一种地图划分方法[17-18]。利用导航网格法对地图进行预处理,需要先利用建模工具对地图中的障碍物进行剔除,生成多边形网格模型地图。利用平面多边形域快速约束Delaunay三角化的方法,可以对生成的约束多边形网格模型进行快速三角划分,生成可运用于寻路算法的导航网格地图[19-21]。因为导航网格预先剔除了障碍物信息,在大面积空白区域的网格划分上,导航网格划分少,所以在路径搜索时,不会考虑障碍物信息,从而搜索的邻居结点也大幅减少,提高搜索效率。
1 多边形导航网格地图三角剖分
多边形导航网格是一组多边形集合,对地图进行可行走域和不可行走域划分。利用建模工具对地图进行处理,剔除障碍物,生成可行走域的多边形网格地图。多边形网格较方格网格地图更容易划分不规则的障碍物,可以有效减少搜索网格的数量,从而提高搜索效率。寻路算法运用于多边形导航网格之前,还需对多边形网格进行三角剖分。
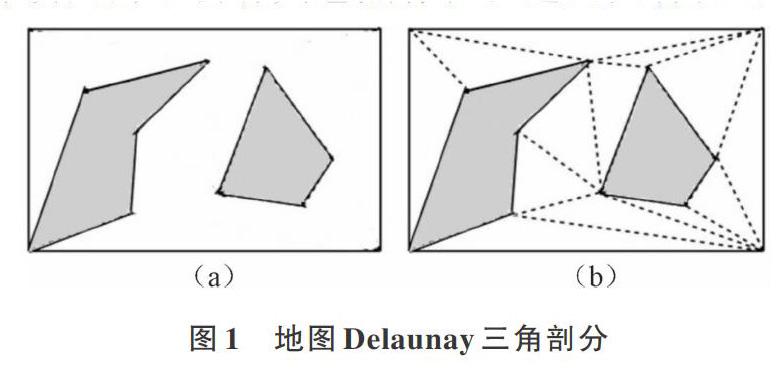
如图1,灰色多边形为障碍物,首先需要将障碍物以及边界的边定义为约束边,如图1(a)中实心线条,完成三角剖分后添加的边称为无约束边,如图1(b)中的虚线条,由此形成的三角网格即为寻路网格。在寻路过程中,可以穿越无约束的边界,但不能穿越受约束的边界。Delaunay三角网具有最大化最小角特性,即Delaunay三角剖分形成三角形的最小角是最大的,因此三角网格是具有规则化的三角网;另一个是空圆特性,即在Delaunay三角网中任一三角形的外接圆内不会有其它点存在。这两大特性可以有效避免出现“长条”细长型的三角网格,生成的三角网格趋近于等边三角形,因此搜索路径不会重复穿越三角网格,保证了三角划分的唯一性,方便网格管理。Delaunay三角划分有很多种方法,例如Bowyer-Watson算法、翻边算法等。在制作多边形导航网格时,已确定受约束边,因此本文在导航网格三角剖分算法上运用了一种快速约束Delaunay三角形剖分的算法。算法如下:
2 A*算法优化
基于多边形导航网格与基于传统方格网格地图的A*算法,相同點是都需要遍历大量结点。为了提高A*算法的搜索效率,减少搜索的网格结点数量,介绍了两种A*搜索结点优化方法:利用二叉堆对搜索结点的Open列表进行存储;利用目标范围界限的方法对目标点进行分区域查找。
2.1 A*算法简介
A*寻路算法是基本的启发式路径搜索算法,它通过启发式函数估计当前结点下一步能到达邻居结点至目标点的成本,以进行路径规划。A*算法是根据加权图制定:从图的特定结点开始,构造从该结点开始的路径树,一次一步地扩展路径,直到其一个路径在预定目标结点处结束为止。在主循环的每次迭代中,A*需要确定将其部分路径中的哪一个扩展为一个或多个更长路径。A*算法核心是启发式函数。
其中,n是当前结点,f(n)表示当前结点n的启发函数,g(n)是从起始结点到n的路径的实际代价,h(n)是估算当前结点到目标结点最优路径的估计成本。h(n)值估算需要引入合适的启发式函数。为了保证用A*找到最短路径,启发式h(x)必须满足结点x和y的以下属性:
D(x,y)为X至Y的实际距离,意味着启发式h(x)的值必须小于或等于实际距离。启发式函数距离估计有很多种方法,例如曼哈顿距离、切比雪夫距离、欧几里得距离等,本文A*算法采用的是二维欧几里得距离。假设点p1=(x1,y1)和点p2 =(x2,y2),其欧几里得距离d(p1,p2)为:
A*算法是使用优先级队列执行要扩展的最小估计成本结点的迭代过程。该优先级队列被称为开放列表,在算法的每一步,从队列中删除具有最低f(n)值的结点,相应地更新其邻居结点的f值和g值,并将该邻居结点添加到Open列表中。 该算法一直持续到目标结点的f值低于队列中的任何结点(或直到队列为空),目标f值就是最短路径的长度,因为h(n)在目标处可接受的启发式函数中为零。A*算法在每次寻路过程中,需要循环遍历大量结点信息,Open列表需要对结点进行存储和判断,进而选取F(n)值最小的结点。
针对基于多边形导航网格的A*寻路算法,提出了两种优化方法,分别是利用二叉堆优化Open列表与利用目标范围界限方法快速找到目标点所在区域。利用二叉堆对结点进行数据存储,可以快速对Open列表中的邻居结点进行插入、删除等操作,从而提高A*算法的搜索效率。利用目标范围界限的方法,可以在预处理地图信息时,对网格进行目标范围划分,生成并保存目标范围界限。当运用A*算法时,读取目标范围界限,即可快速定位目标点所在范围,从而减少搜索的结点数量。
2.2 Open列表数据结构优化
大型地图中具有数量巨大的网格结点,需要反复搜索数据量庞大的Open列表,从而导致搜索效率过低。为了解决这一问题,引入二叉堆对结点进行数据存储,对A*算法进行优化。
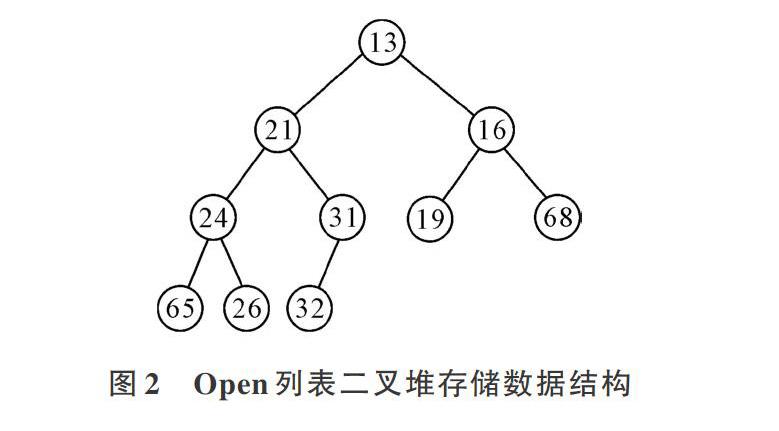
二叉堆是一种特殊的堆,特殊之处在于它是完全按照大小顺序存储的完全二叉树。其有最小二叉堆和最大二叉堆,最大二叉堆的堆结点即父结点是最大的,相反最小二叉堆是最小的。二叉堆的堆序性是,任意一个父结点中的键值总是小于或等于子结点中的键值,这样就可以快速执行数据操作。在Open列表中,需要考察F(n)的最小值,因此采用最小二叉堆存储Open列表中的结点。图2为Open列表二叉堆示例图,圆圈中数字代表F(n)值。
引入二叉堆后,A*算法每执行一次寻路过程,就需要对Open列表进行更新,增加邻居结点,删除Open列表中无用的结点。
插入数据,需要在二叉堆下一个可用位置创建一个空穴,如果不会破坏数据顺序结构,则插入成功。若不符合数据顺序则继续向上插入,直至成功。
删除数据,只能删除根结点,在根结点处建立一个空穴,将二叉堆最后一个值赋予根结点,自上而下依次调整,直至满足二叉堆的堆序性。
利用二叉堆存储Open列表可快速插入和删除列表中邻居结点,从而提高A*算法的搜索效率。
2.3 基于目标范围界限的优化
目标范围界限是一种在预处理地图信息时快速划分目标点的方法,核心思想是预先计算一个边界框,其中包含所有通过探索其边达到目标最优路径的结点。在进行地图预处理时,对应边界框的参数也相应被存储。当运行寻路算法时,可以实时读取存储边界框的参数,从而只需要对目标结点所处目标范围边界框内的结点进行考察,从而减少所搜索的结点数量,提高搜索效率。
计算目标范围界限的方法为:
(1)定义选取起始点邻接方向的邻居结点,如图3(a)所示,起始结点分别有A、B、C等3个邻接方向。
(2)利用Dijkstra算法遍历邻接方向所有结点,记录从起始点出发进行该方向探索的最优路径点,并作标记。如图3(a)中标记C的三角网格结点,探索下方网格,只有通过标记C的网格才是该方向最优路径的网格结点。
(3)当计算完所有网格结点时,划分生成目标结点的范围界限,并且存储在相应文件中。
(4)在運用寻路算法之前,读取文件中的目标界限参数,寻路算法只需对目标点所在目标范围界限中的结点进行考察。
3 优化A*算法实现
优化后的A*算法,同样适用于多边形导航网格。方格地图网格都是规则的正方形网格,因此在计算网格距离时,只需要计算网格中心点之间的距离。与方格网格地图不同,经Delaunay剖分所形成的三角网络导航网格具有不规则性,导致G(n)值和h(n)的计算不能统一。因此,为了统一三角网格自身耗费以及提高估价函数的准确性,需要对G(n)值和h(n)的计算方法加以改进。
改进策略:G(n)为当前三角网格至下一个网格代价总和,H(n)为三角形中心到目标三角中心的距离。如图4,三角网格自身代价为穿入边AB中点至穿出边AC中点的距离。
4 漏斗算法路径平滑处理
基于多边形导航网格的优化A*算法生成路径如图5,实线为实际最短路线,虚线为A*算法寻路生成的路径,是三角形内心所连接成的线段,并不能代表其最优真实路径,需要进一步利用漏斗算法进行路径平滑处理,从而生成实际最优路径。
漏斗算法包括3种结构:路径、漏斗和顶点。路径是构成算法中已知最短路径点的一系列线段,漏斗边分别由顺时针旋转边和逆时针旋转边组成,涵盖尚未处理的最短路径区域。多边形顶点以顺时针方向保存(见图6)。
在算法开始时,路径为空,顶点设置为起点S,分别连接内部最近的顶点V1和V2,构成漏斗进行判断。若接下来的顶点在漏斗边SV2和SV1内部,则更新漏斗,如图6(a)所示;若V3和V4都在漏斗里面,则更新漏斗边SV3,漏斗将变得更窄;若顶点在漏斗边的外边则无需更新漏斗,如图6(b)中V5在漏斗边SV3的右边;若漏斗上边的顶点在下边的下方,如图6(c)中V8已经在下边漏斗边的下方,则需要重置漏斗的顶点。由V3作为顶点,分别连接V4、V5重新构造漏斗,存储点V3作为拐点之一。重复执行以上步骤,处理所有最优路径的三角网格顶点,存储拐点,最终得到V3、V8为拐点,连接所有拐点找到最优路径。图6(d)中S-g线段即为最优路径。漏斗算法如下:
输入:s起始点,g终点
输出:Path Π(ΔS,ΔE)
(1)if (NumEdges(c)<1)
(2)p.Add(s);p.Add(g);
(3)return P;
(4)L1← Connect(s,pr) : L2← Connect(s,Pl);//构造漏斗边L1和L2,顺时针旋转,在下方的为L1称为漏斗的右边。
(5)While (p.rightside !=null) { //遍历路径右侧的点
(6)If(pr+1 in L1.Leftside And pr+1 in L2.Rightside) //判断下一个漏斗右边方向的多边形顶点是否在漏斗里面,若是,则更新漏斗边,漏斗边收窄。
(7)update L1← Connect(s,pr+1 ) ;
(8)else If (pr+1 in L2.Leftside)
(9)update L1← Connect(pr,pr+1) And push pr in CornerPoint[] ;//重置漏斗顶点以及边,并存储顶点作为//拐点。
(10)else If (pr+1 in L2.Leftside ) do nothing;}
(11)同理处理漏斗左边的顶点,存储拐点;
(12)Connect (s, CornerPoint[] ,g) ;//连接起始点、拐点和终点形成路径。
(13)return path P(s,CornerPoint[] ,g);
5 实验仿真及评估
本文实验平台搭建利用Unity3D游戏引擎,地图制作利用Blender建模工具,分别制作10×10、20×20、50×50尺寸的实验地图,对应尺寸均为Unity单位,制作好的地图需要对障碍物进行剔除,并删除内部网格线,生成多边形轮廓的导航网格。在方格地图的生成上,根据障碍物尺寸,选择合适尺寸的网格。为了更精确寻找最优路径,选择0.1Unity单位的网格地图,对地图进行遍历,确保寻路的准确性。地图预处理生成的目标范围界限以XML形式保存在项目文件夹中(见图7)。
经过实验对比分析,在保证最优路径的基础上,地图面积越大,基于多边形导航网格地图的改进A*算法在搜索结点以及搜索时间上越优于基于传统方格地图的A*算法(见图8)。
6 结语
本文是针对不规则凸多边形的A*寻路算法研究,对凸多边形地图利用快速约束Delaunay三角剖分的方法进行三角剖分,形成可用于寻路的三角网格。为适用于不规则的三角网格,改进统一A*算法中的网格代价,并给出针对多边形导航网格的优化A*算法。生成路径是三角网格中心点的连线,并不是实际的最优路径,因此需要利用漏斗算法对路径进行平滑处理。本次实验地图采用的是二维地图,多边导航网格在三维地图中也有良好的表现。未来将重点研究如何将优化A*算法运用于三维多边形导航网格。
参考文献:
[1] 何国辉, 陈家琪. 游戏开发中智能路径搜索算法的研究[J]. 计算机工程与设计,2006, 27(13):2334-2337.
[2] 詹海波. 人工智能寻路算法在电子游戏中的研究和应用[D]. 武汉:华中科技大学, 2006.
[3] 李井颂. 游戏中的智能路径搜索算法及其应用[D]. 昆明:昆明理工大学, 2017.
[4] 张前哨. 基于A算法的地图寻径的研究[D]. 武汉:武汉科技大学, 2005.
[5] HARABOR D,GRASTIEN A. Online graph pruning for pathfinding on grid maps[C]. San Francisco:AAAI Conference on Artificial Intelligence, 2011.
[6] DEMYEN D,BURO M. Efficient triangulation-based pathfinding[J]. Aaai,2007,1338(9):161-163.
[7] DEKIM H,YU K,KIM J. Reducing the search space for pathfinding in navigation meshes by using visibility tests[J]. Journal of Electrical Engineering & Technology,2011,6(6):867-873.
[8] KALLMANN M. Navigation queries from triangular meshes [C]. The Third International Conference on Motion in Games,2010:230-241.
[9] 王天顺,张莉. 一种基于导航网格的路径搜索技术[J]. 电脑知识与技术,2010,6(12):3014-3016.
[10] 陳娜,黄明和,刘清华. 基于DAF算法的地图寻径研究[J]. 科学技术与工程,2010,10(30):7536-7540.
[11] 张翰林,关爱薇,傅珂,等. Dijkstra最短路径算法的堆优化实验研究[J]. 软件,2017, 38(5):15-21.
[12] 孙玉昕,章瑾. 利用堆排序优化路径搜索效率的分析[J]. 武汉工程大学学报,2013, 35(6):50-54.
[13] WAGNER D,WILLHALM T,ZAROLIAGIS C. Geometric containers for efficient shortest-path computation[J]. Journal of Experimental Algorithmics,2005,10(10):1-3.
[14] 韩玮. 游戏地图寻路及其真实性研究[D]. 重庆:西南大学, 2013.
[15] 周振华. 游戏场景中分层寻路算法及地图复杂性度量研究[D]. 石家庄:河北大学,2014.
[16] 李立,唐宁九,林涛. 基于地图分割与以矢量信息描述地图的A*寻路算法[J]. 四川大学学报:自然科学版,2010,47(4):729-734.
[17] 王烨萍. 基于综合导航网格的智慧旅游动态寻径方法[D]. 成都:西南交通大学, 2017.
[18] 林巍凌. 引入导航网格的室内路径规划算法[J]. 测绘科学, 2016,41(2):39-43.
[19] 赵芳垒,敬石开,李向前,等. 基于三角形细分的三角网格模型表面体素化算法[J]. 计算机集成制造系统,2017,23(11):2399-2406.
[20] 严冬明,胡楷模,郭建伟,等. 各向同性三角形重新网格化方法综述[J]. 计算机科学, 2017, 44(8):9-17.
[21] 曾薇,孟祥旭,杨承磊,等. 平面多边形域的快速约束Delaunay三角化[J]. 计算机辅助设计与图形学学报,2005,17(9):1933-1940.
(责任编辑:何 丽)
