巧用“降维”思想 解决物理立体图难题

钱启明

(江苏省启东市第一中学 226200)

三维视图问题对学生空间思维能力和综合处理问题能力要求高，多数同学会觉得问题所描述的情况无法想象，无法熟练的运用知识来解决这类问题.学生在数学中已经了解了三视图的方法，所以需要做的就是引导学生运用这个方法解决物理问题.

一、运动方向一分为二，化繁为简

在很多力学问题当中，物体运动除了直线外，会遇到某些特殊的运动轨迹，这样的运动方式让受力分析成为难点，我们不妨换一个思路，将复杂运动分解为若干简单运动，化繁为简，让复杂运动不再复杂.

例1某人骑电动车车在圆筒形内沿着筒壁骑行.电动车加速行驶直到可以在筒壁上以匀速骑行，如图1所示.如果电动车(包括人)的总质量为M，筒壁半径为R，匀速率行驶的速率为v，每行驶一圈上升h，求电动车匀速行驶时的向心力.

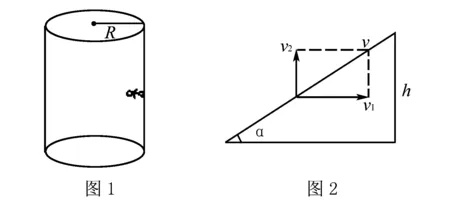
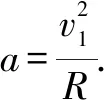
点拨从本题我们可以了解，运动不仅包括直线运动还包括各种复杂运动，而我们要做的就是删繁就简，将复杂问题简单化，在分析当中抽丝剥茧，这就需要同学们掌握数学知识和物理知识，以便从容应对此类问题.

二、立体电阻分解，一目了然

物理的电磁学当中少不了与电阻打交道，平面的电阻电路图是非常常见的，但是如果遇到立方形的电阻是不是还能从容应对呢，这就需要我们用一定的技巧进行简化，让立体变平面.

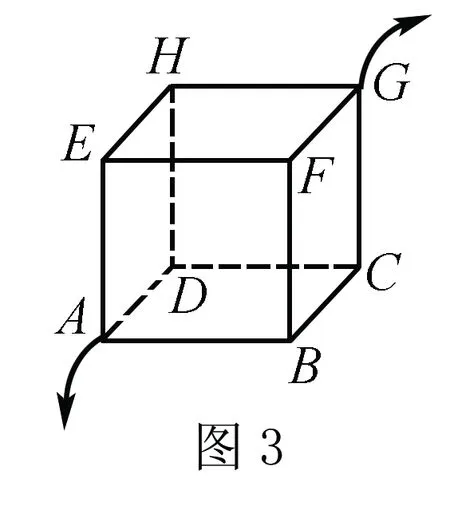
例2如图3所示，某立方形是用12根阻值均为r的电阻丝构成.求立方形当中A点和G点之间的等效电阻.

解析我们看到电路是由立方形组成，现将该立体电路“压平”成平面电路图，如图4所示.

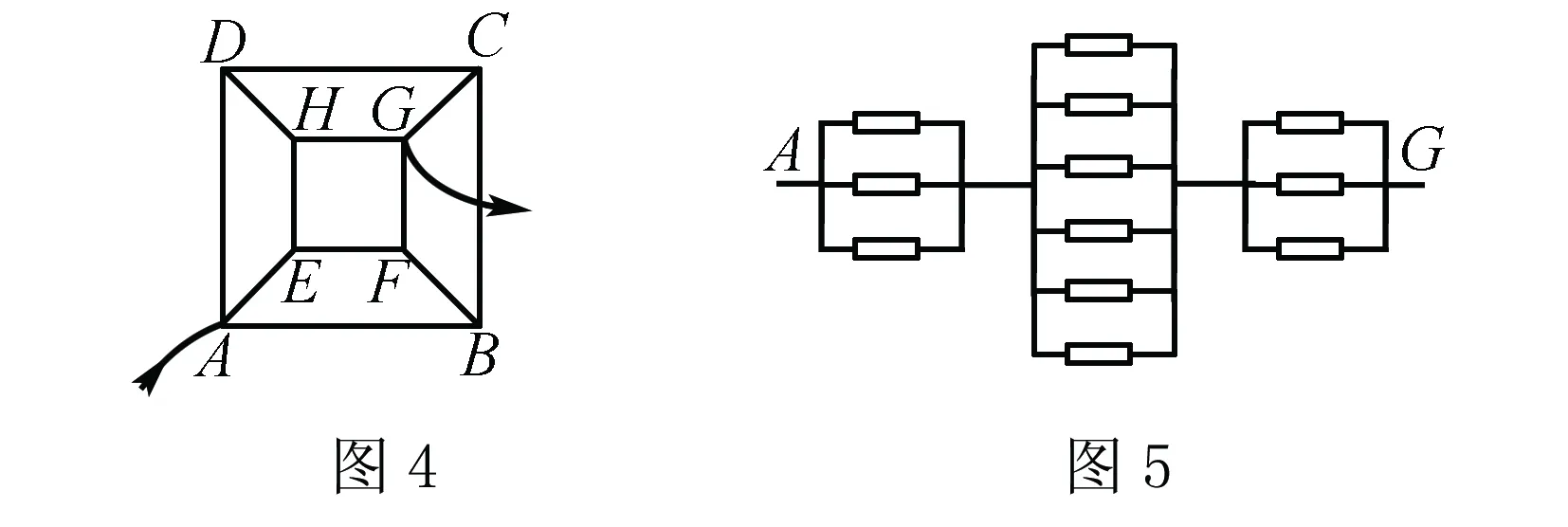
由于到D、E、B三点等势，C、F、H三点等势，则立体电路可等效为如图5所示的电路图，所以A点和G点之间总电阻为

点拨电磁学问题是物理学的重中之重，掌握电磁学的各种解题方法是非常必要的，但是同学又不能拘泥于物理学当中，这里就非常典型的运用了数学当中的几何知识，是立体变平面的典型问题.

三、斜面变平面，信手拈来

此问题的图形是三维的，不容易掌握物体的加速度，难度增加．如果我们能通过三视图将三维变成二维，问题就会容易得多.我们可以将立体图用三视图法，将分解成由两个运动轨迹的合体，这样解决起来可谓信手拈来.

例3如图6(1)所示光滑带有斜度的平面长为a，宽为b，斜度为α，现有一个圆球在斜面上方P点水平抛出，要想使圆球从Q点离开，则需要圆球的初速度v0是多少.

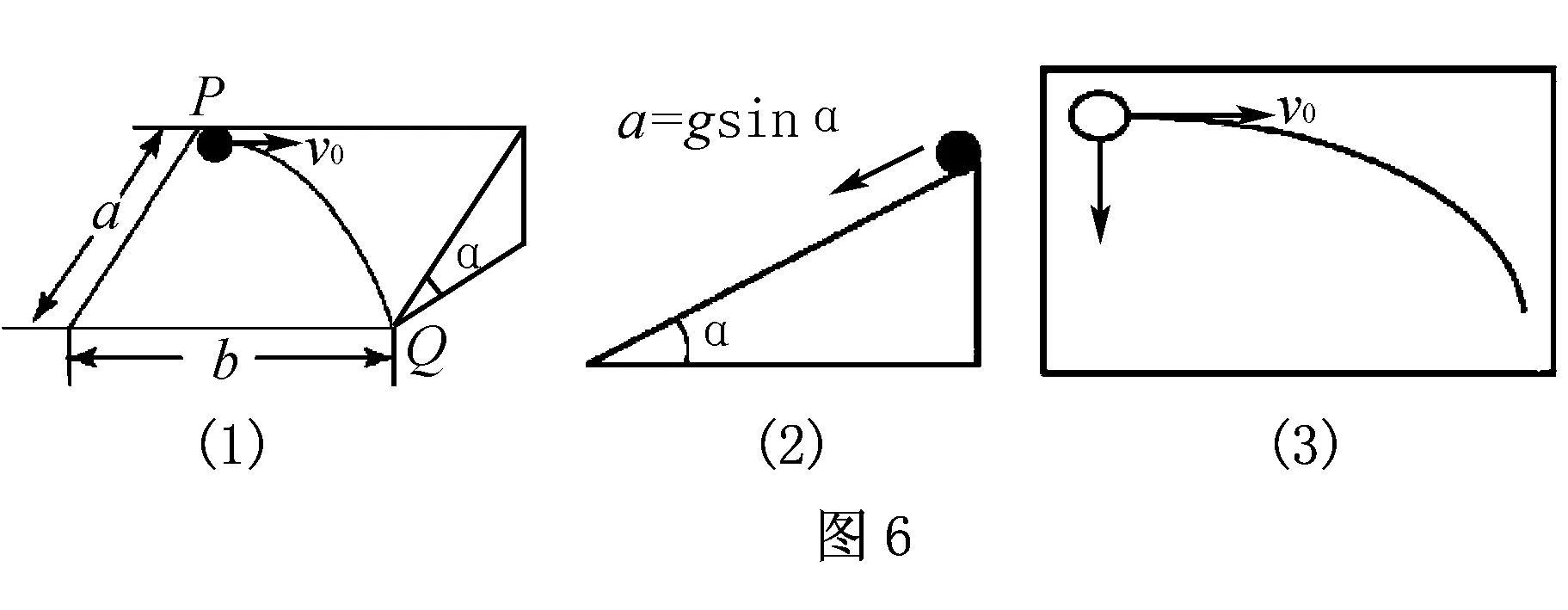
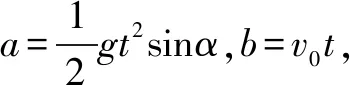
点拨三维运动分解为两个或者若干个平面运动，是解决此类问题的关键所在，也是让复杂问题简单化的“黄金钥匙”，深刻理解题意是前提，熟练掌握数学、物理知识是基础，灵活的思维是途径，正确分解图形是“钥匙”.

以上三个例题分别介绍了三种“降维”方法，在以后的学习当中还需要同学自己摸索，自己探究，把数学几何思维和物理结合起来，不再让立体图成为难点，化繁为简，数形结合，以发散的思维看问题，这是学习的正确路径之所在.