利用时间序列模型对甘肃省GDP进行预测与决策

魏艳华，王丙参，包丽莉

（天水师范学院 数学与统计学院，甘肃 天水 741001）

国民生产总值（GDP）反映了某地区总体经济状态，是政府制定宏观经济政策的主要依据.另外，GDP也常常作为预测模型的重要变量，非常重要.[1]正是因为以上原因，许多学者利用各种模型与算法对GDP进行预测，以便对国民经济发展提供决策依据.[2-4]对GDP数据构成的时间序列进行预测，主要方法有两类：[4]一是确定性分析，如曲线回归、移动平均法、灰色预测法等，其结果易于解释，但由于该类方法只利用了确定性信息，没有利用随机信息，故精度有限；二是随机性分析，比如ARIMA模型、条件异方差模型，这类方法不仅利用了确定性信息，也利用了随机信息，提高了精度，但缺点是不便于直观解释.本文根据甘肃省1978～2016年的GDP，分别建立了ARIMA模型与两个残差自回归模型并进行比较分析，建议优先采用利用延迟因变量建立的残差自回归模型进行预测，并对预测结果进行分析，对政府制定经济策略提供参考.

1 基于ARIMA的甘肃省GDP预测

对差分平稳时间序列（即经差分后会变为平稳时间序列的非平稳时间序列）可以用ARIMA模型进行拟合.[1-3]ARIMA(p,d,q)模型结构如下：

对于一个时间序列，首先要进行预处理，即平稳性检验与白噪声检验.平稳性检验方法主要有：

（1）时序图法.根据平稳序列的均值和方差均为常数可知，平稳序列的时序图应该始终在一个常数附近随机波动，且波动范围有界，反之则否.

（2）自相关图法.通常，平稳序列有短期相关性，故其延迟k期自相关系数 ρ̂(k)会快速衰减向0，反之，ρ̂(k)衰减向0的速度较慢.

（3）单位根检验.

Barlett证明[4]：对于n期纯随机观测序列

（1）假定原假设

其中m为延迟期数；

（2）构造检验统计量

Box和 Pierce[4]推导出当统计量或 p值小于显著性水平 α时，则以1-α的水平拒绝H0，即该序列不是纯随机序列.在大样本场合，Q统计量的检验效果很好，但是在小样本场合就效果较差，为此Box和Ljung又推导出统计量[4]，它适合各种场合，人们普遍使用的是LB统计量.注意，延迟期数m的选择会影响LB的统计表现，通过蒙特卡罗方法可知取m≈ln(n)会有较好的功效.

下面利用ARIMA模型对甘肃省GDP进行预测.

（1）获取甘肃省GDP观测值序列.

从《国家统计年鉴》(2017)获取甘肃省1978年至2016年的GDP数据，见图1与SAS程序（单位：亿元）.1978年之前，中国政策多变，且与改革开放后有很大差异，故1978年之前GDP数据不选用.

图1 甘肃省GDP时序图

根据甘肃GDP时序图（见图1）容易判定：1978年至2016年，甘肃省GDP整体呈上升趋势，刚改革开放时，基数小，增长幅度也不大，从2000年以后，GDP增长很快，但最近几年增速放缓，初步判定甘肃省GDP序列为非平稳时间序列.特别注意，甘肃省2015年的GDP略微下降，这主要由中国当前社会经济大环境严峻以及甘肃特殊的自然与社会环境导致.另外，从GDP的自相关图（略）也可发现，自相关函数缓慢衰减到2倍标准差内,这是明显的非平稳特征.因此，可断定GDP序列是非平稳时间序列.

（2）尝试对原序列进行ARIMA建模.

经初步尝试，直接对原GDP序列建立ARIMA模型，效果很差（残差序列是非白噪声序列）.这是因为：在实践中，很多金融时间序列（GDP以货币衡量，也可认为是金融时间序列）呈现一定异方差性质，且通常序列标准差与序列均值有某种正比关系.原序列2阶差分后的时序图（见图2）也显示波动随时间而变化，且有增大趋势，这也佐证了其异方差性.

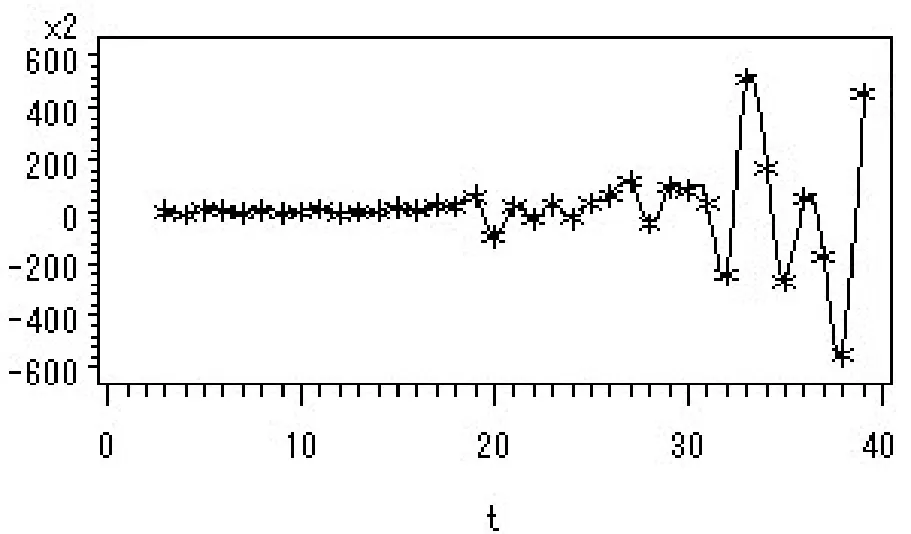
图2 原序列2阶差分后的时序图

将转换函数g(xt)在序列均值 μt处进行一阶泰勒展开：则

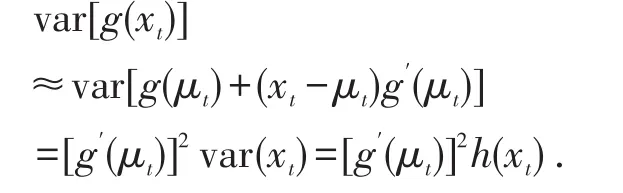
（3）利用对数序列进行ARIMA建模.

现对原序列进行对数变换，由对数序列时序图（见图3）可知，对数序列ln xt保持了原序列的变化趋势，且大致呈一条直线，故利用一阶差分运算提取线性趋势.由ln xt的一阶差分时序图（见图4）可知，一阶差分运算已经成功从原序列提取了线性趋势，差分后序列可初步认定为平稳序列.由自相关图可知，自相关系数快速落到2倍标准差内，故可认为对数序列ln xt的一阶差分后序列（记为dif(ln xt)）是平稳的.对dif(ln xt)进行白噪声检验可得：延迟6阶QLB统计量值为13.72，p值为0.0330，小于0.05，故dif(ln xt)是非白噪声序列，有进一步分析的价值.

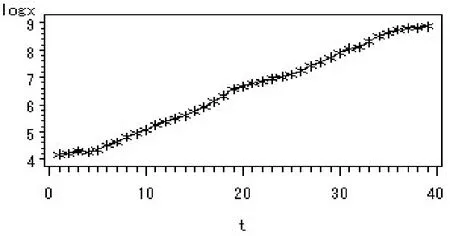
图3 甘肃GDP取对数后的时序图

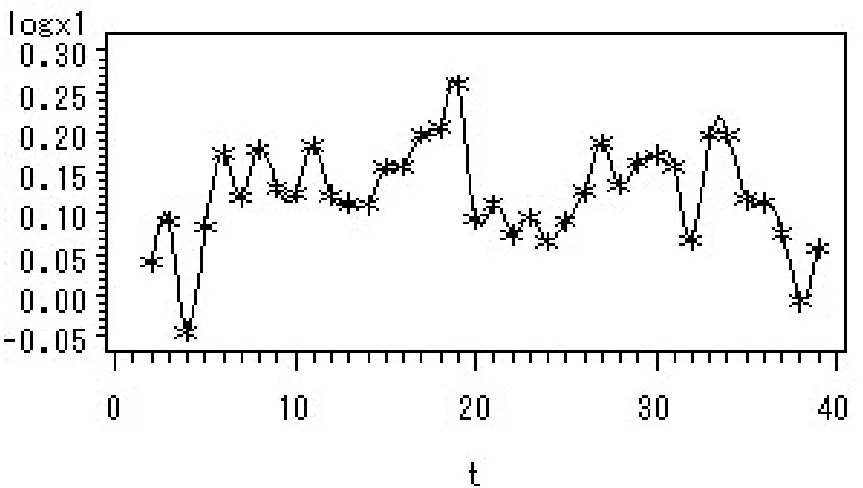
图4 对数序列的一阶差分时序图

图5 一阶差分序列的自相关图

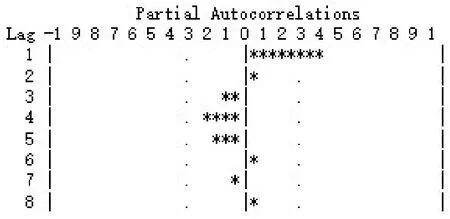
图6 一阶差分序列的偏自相关图

显然，自相关图（见图5）拖尾，偏自相关图（见图6）一阶截尾，所以对序列ln xt可建立ARIMA(1,1,0)模型.

SAS程序主体如下：

data gsgdp;

inputx@@;t=_n_;

logx=log(x);

logx1=dif(logx);

cards;

64.73 67.51 73.9 70.69 76.88

91.5 103.17 123.39 140.74 159.52

191.84 216.84 242.8 271.39 317.79

372.24 453.61 557.76 722.52 793.57

887.67 956.32 1052.88 1125.37 1232.03

1399.83 1688.49 1933.98 2277.35 2703.98

3166.82 3387.56 4120.75 5020.37 5650.2

6330.69 6836.82 6790.32 7200.37;

proc gplotdata=gsgdp;

plotx*t logx*t logx1*t;

symbol c=black i=spline v=star;

run;

proc arima data=gsgdp;

identify var=logx(1);estimate p=1;

forecast lead=3 id=tout=gsgdpjg;

run;

data gsgdpjg;

setgsgdpjg;

x=exp(logx);l95=exp(l95);u95=exp(u95);

forecast=exp(forecast);

run;

proc printdata=gsgdpjg;

var t forecast;where t＞39;

run;

部分输出结果如下：

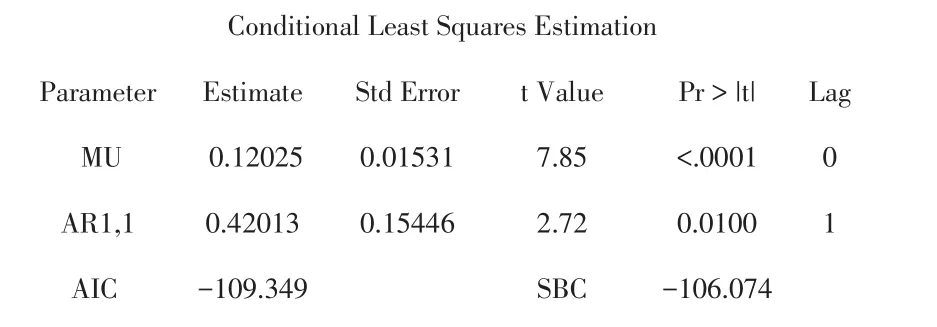
显然，序列ln xt的拟合模型为ARIMA(1,1,0)，模型为

且系数显著性检验的 p值分别为＜.0001，0.0100，通过了显著性检验.根据最小信息准则，本模型的AIC=-109.349，SBC=-106.074.

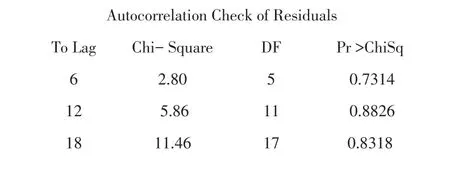
对于残差序列的白噪声检验，延迟6阶的 p值为0.7314，显著大于0.1，这表明：模型的残差项中不再显著蕴含与样本有关的信息，即构建ARIMA(1,1,0)模型有效.

显然，序列ln xt未来3期的预测值分别为8.9763,9.0856,9.2013.

将其进行对数转化后可得甘肃2017-2019年的GDP预测值为7912.90，8827.46，9910.02亿元.从整体看，甘肃省GDP预测值的相对误差控制在5%的范围内，预测结果较理想，拟合效果如图7所示.

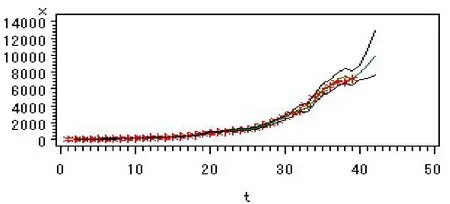
图7 拟合效果图

实际上，甘肃省2017年的GDP为7677.0亿元，仅比上年增长3.6%，而利用ARIMA模型的预测值为7912.90亿元，高估较多.这是因为，2017年复杂多变的国内外环境和多年少有的严峻形势导致了如此低的增长率，低于2016年4个百分点.这说明当前环境相对往年有较大变化，而ARIMA模型有效的前提是当前环境基本平稳.最后，希望政府能改变观点，吸引人才，创造良好的商业环境，盘活经济.

2 基于残差自回归模型的甘肃省GDP预测

残差自回归模型既利用了确定性信息，也利用了随机性信息，故精度高，又便于解释，[5-8]其模型结构为：

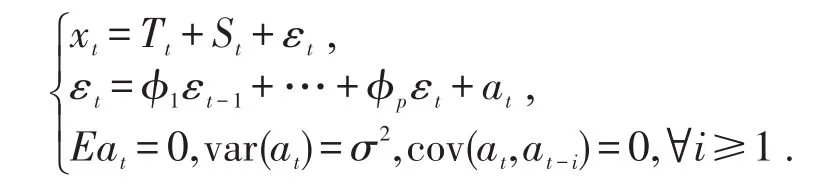
其中Tt是趋势效应拟合，St是季节效应拟合，εt为残差序列.

残差自回归模型1：由于甘肃省GDP时序图呈抛物线趋势增长且没有周期，故考虑采用时间t的幂函数作为自变量，即采用拟合趋势效应.

SAS程序主体如下：

datagsgdp;

inputx@@;

t=_n_;t2=t**2;

cards;

数据

;

proc autoreg data=gsgdp;

modelx=t t2/dwprob;

modelx=t t2/nlag=5 backstepmethod=m lnoint;

outputout=wang p=xp pm=xtrend;

run;

部分输出结果如下：

显然，DW统计量的值为0.1760，正相关检验的p值＜.0001，故残差序列显著正相关，应对残差建立自回归模型.

显然，最终拟合残差自回归模型为

在显著性水平α=0.05下，模型系数都通过了显著性检验.

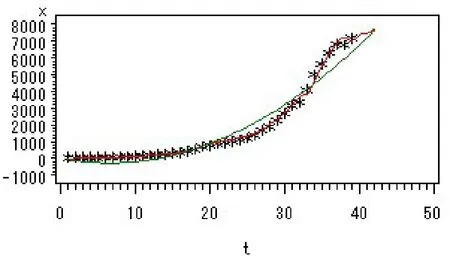
图8 拟合效果图

显然，本模型的 AIC为500.330585，SBC为506.984831.注意，此处的AIC、SBC与ARIMA模型中的AIC、SBC不能直接比较，因为它们对应的时间序列是不同的.进一步，趋势拟合部分的R2为0.9315，整体拟合模型的R2高达0.9980，另外，拟合值的相对误差控制在理想范围内，故拟合效果（见图8）好.相对于二次曲线回归模型，R2由0.9696提升到0.9980，最小信息量SBC由585.461638下降为506.984831，这表明残差自回归模型提高了预测精度.

在SAS程序数据步，将甘肃GDP数据最后三个定义为缺失数据即可进行3期预测，见表1.

表1 三期预测值

可见，甘肃省2017～2019年GDP整体预测值分别为7374.946909,7492.630553，7717.752566亿元.

残差自回归模型2：下面建立延迟因变量回归模型，建模思路同上，SAS程序主体为：

data gsgdp;

inputx@@;

lagx=lag(x);

cards;

数据

;

proc autoreg data=gsgdp;

modelx=lagx/dwprob;

model x=lagx/nlag=5 backstep method=ml noint;out⁃

putout=wang p=xp;

run;

部分输出结果为：

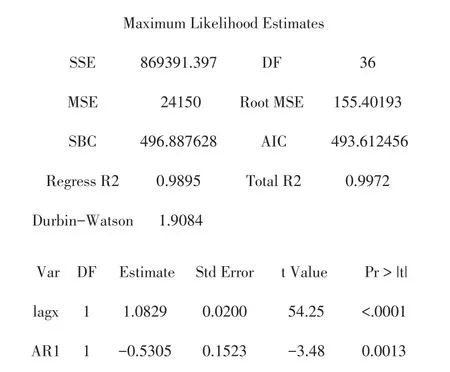
最终拟合模型为：

本模型的R2为0.9972，稍微低于残差自回归模型1，AIC为493.612456，SBC为496.887628，这两项指标都优于残差自回归模型1，MSE为24150，大于残差自回归模型1.此模型可解释为：在外界没有突变的情况下，甘肃省GDP每年递增8.29%，且以上期残差的0.5305倍进行修正，即本模型具有一定的自我修正功能.自我修正就是统计学习，其目的是使学到的模型对已知数据与未知数据都具有较好的预测功能，从而使模型更能适应外界的变化.进一步可得，一期预测值为7716.0051895亿元.

3 结 论

采用共同标准可对三个模型进行直接比较，如果以MSE为标准，由于取对数后建立ARIMA模型（简称取对数ARIMA模型）的MSE为27992，最大，所以对于本文建立的三个模型，对数ARIMA模型的效果最差，残差自回归模型1最优.但是，对于2017年GDP的真实值而言，残差自回归模型2预测值的误差最小，仅仅高估39亿元，且模型便于直观解释，而残差自回归模型1预测值的误差最大，低估303亿元.从模型的复杂度而言，对数ARIMA模型经多对数运算与差分运算后，采用了3个变量，残差自回归模型1直接采用了5个变量，而残差自回归模型2仅仅采用了3个变量，故残差自回归模型2最简单.在所有可选择的模型中，能够解释已知数据且非常简单的模型才是好模型，故优先选择残差自回归模型2.另外，最近几年，国内外环境变化很大，中国GDP增速放缓，个别省份在某些年份甚至出现负增长，这也导致利用延迟变量建立的残差自回归模型更有效，即残差自回归模型2的适应性强，因此，在外界环境变化较大情况下，其预测精度可能更高.综上所述，对甘肃省GDP进行预测，可优先选用残差自回归模型2，因为它更能适合外界环境的变化.

ARIMA模型利用差分提取确定性信息，并对随机信息建立ARMA模型，提高了估计精度，但不便于经济解释.残差自回归模型结合了确定性分析与随机性分析的优点，精度较高，且经济意义直观.另外，延迟1阶因变量的自回归模型与AR（1）模型是不同的，AR(1)模型只能对平稳序列建模，而前者既可以对平稳序列建模，也可以对非平稳序列建模，适用面更广.