基于元胞自动机数学模型的瓦斯抽采管道漏点定位研究*

2019-06-05张丽娜

中国安全生产科学技术 2019年5期

张丽娜，白珊

(唐山科技职业技术学院，河北唐山 063000)

0 引言

随着我国煤矿开采深度的加深，矿井瓦斯涌出量一直处于上升状态，瓦斯对煤矿安全生产构成重大危险[1-2]。但是瓦斯又是优质的清洁能源，因此需要加大煤矿瓦斯的抽采利用。然而，瓦斯抽采管路存在老化生锈以至于漏气的情况。在抽采负压的情况下，管道容易混入空气，不仅使抽采效率降低，而且会造成瓦斯爆炸[3-4]。因此，瓦斯抽采管道泄漏监测与漏点定位技术已成为煤矿瓦斯抽采管道安全运行，提高抽采效率和避免事故发生亟需解决的问题。

自20世纪70年代末，国内外众多学者进行了长期的管道泄漏基础理论和实验研究。根据监测时使用的技术手段不同可以分为基于硬件的方法和基于软件的方法。随着计算机技术的发展，以数据采集与监控系统(SCADA)为基础的实时检漏监测技术逐步兴起。由于其成本较低，可控性强[5-7]，该系统将计算机技术、信号处理技术和传感技术等融合在一起，通过安置在管道上的传感器实时采集温度、流量、压力等信号，泄漏位置得以通过漏点定位算法确定。但是有些算法对影响管道流体状态的因素进行简化，误差大，精度不高，不能对泄漏点进行精确定位，而且将实时检漏监测技术应用到瓦斯抽采管道上的研究甚少。因此本文尝试利用元胞自动机(CA)模型进行漏点的精确定位，对瓦斯抽采管道进行实时监测。该算法通过CA在空间和时间上离散化的特性来演化管道流体在时空上的连续变化，能够很好地求得管道沿程压力，从而进一步提高定位精度。

1 模型建立

1.1 元胞自动机

元胞自动机(Cellular Automation，简称CA)是一种动力系统，在时间、空间上都呈离散状态[8-15]。散布在规则格网中的每一个元胞(cell)取有限的离散状态，遵循同样的作用规则，依据确定的局部规则同步更新，如图1所示。一般元胞自动机是一个四元组A=(L,S,N,f)，其中L表示元胞空间；S是元胞有限的离散状态集合；N表示所有邻域内元胞的集合，即包含有n个不同元胞状态的空间向量；f为演化规则。

图1 元胞自动机的组成Fig.1 Composition of cellular automata

1.2 漏点定位模型

本文所提出的瓦斯抽采管道泄漏定位模型主要针对同一工作面或者采区的主管道。在同一采区或者工作面内的管道落差较小，因此忽略高程变化，气体管道稳态模型满足质量、动量和能量守恒的管流方程组为：

(1)

(2)

(3)

式中：ρ为流体密度，kg·m-3；w为流体体积流量，m3·s-1；λ为水力摩阻系数；x为管道的轴向长度，m；P为压力，Pa；D为管道内径，m；h为焓，J·kg-1；F为单位质量流体的交换热，J·kg-1；∂F/∂x为单位质量流体在单位管长上的热交换率，J·kg-1m-1；A为管道截面积，m2。

描述气体密度和温度、压力间关系的气体状态方程：

P=f(ρ，T)

(4)

式中：P为压力，Pa；ρ为流体密度，kg·m-3；T为温度，℃。

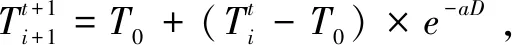
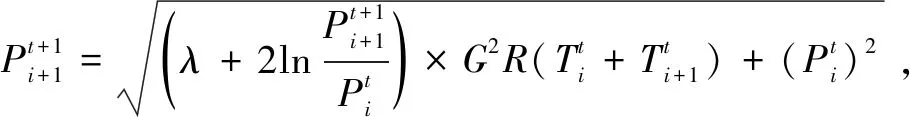
(5)

当管道发生泄漏时，管道始末端压力、温度和流量传感器采集到的管道始末端压力为P1，Pn，管道始末端温度为T1，Tn，管道始末端体积流量为w1，wn。可以将管道以漏点为分界点分为2段，如图2所示。

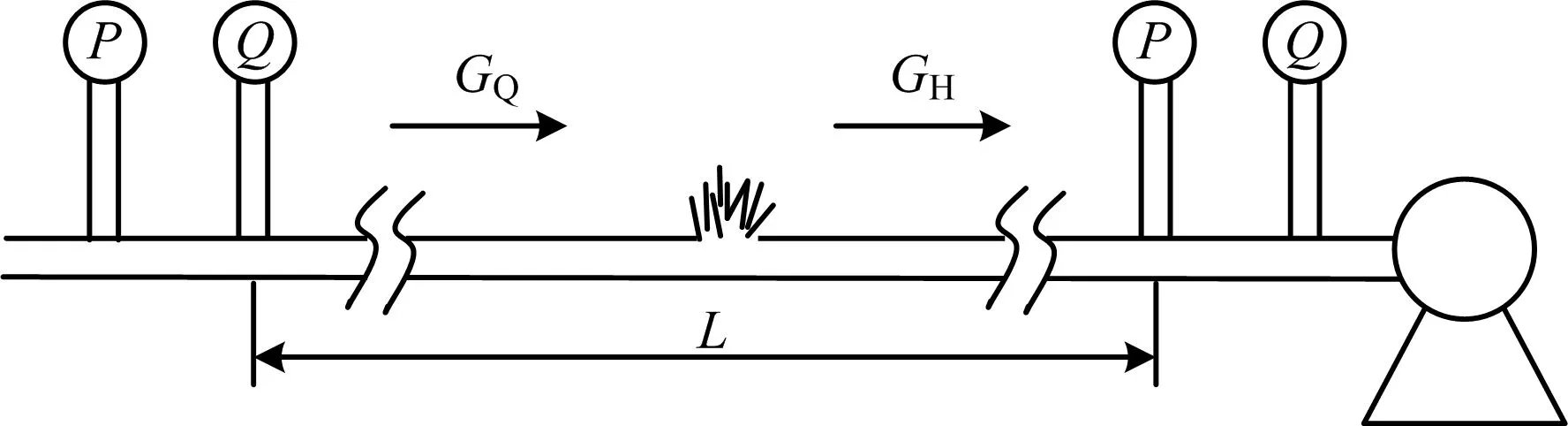
图2 管道泄漏示意Fig.2 Schematic diagram of pipeline leakage

(6)

根据元胞自动机模型可得未发生泄漏时，管道沿程压力如图3中曲线1所示，当管道发生泄漏时，根据始端压力和体积流量可以得到管道始端至漏点沿程压力分布如曲线ABC′所示，根据末端压力和体积流量可以得到漏点至管道末端压力分布，如曲线A′BC所示。由图3可知，曲线ABC′，A′BC交点即为泄漏点。

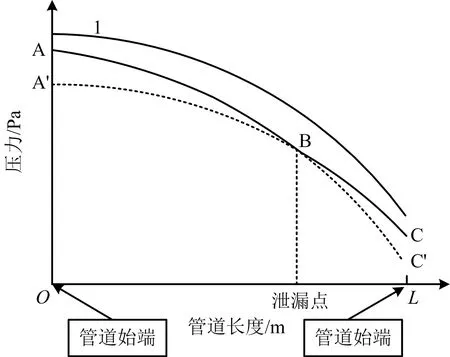
图3 管道沿程压力Fig.3 Pressure along pipeline

2 实验验证

2.1 实验系统

实验系统包括管道系统、数据采集系统和漏点定位系统。管道系统由真空泵、实验管道和管构异件组成，而管构异件包括球阀、三通管、法兰盘、管接头、90°弯头；数据采集系统包括管道始末端的压力变送器、涡街流量计、监控分站和光端转换机；漏点定位系统为监控中心站，包括上位机、中心站主机。1～6为测点，其中测点2，3，4，5为阀门，作为模拟口，如图4所示。

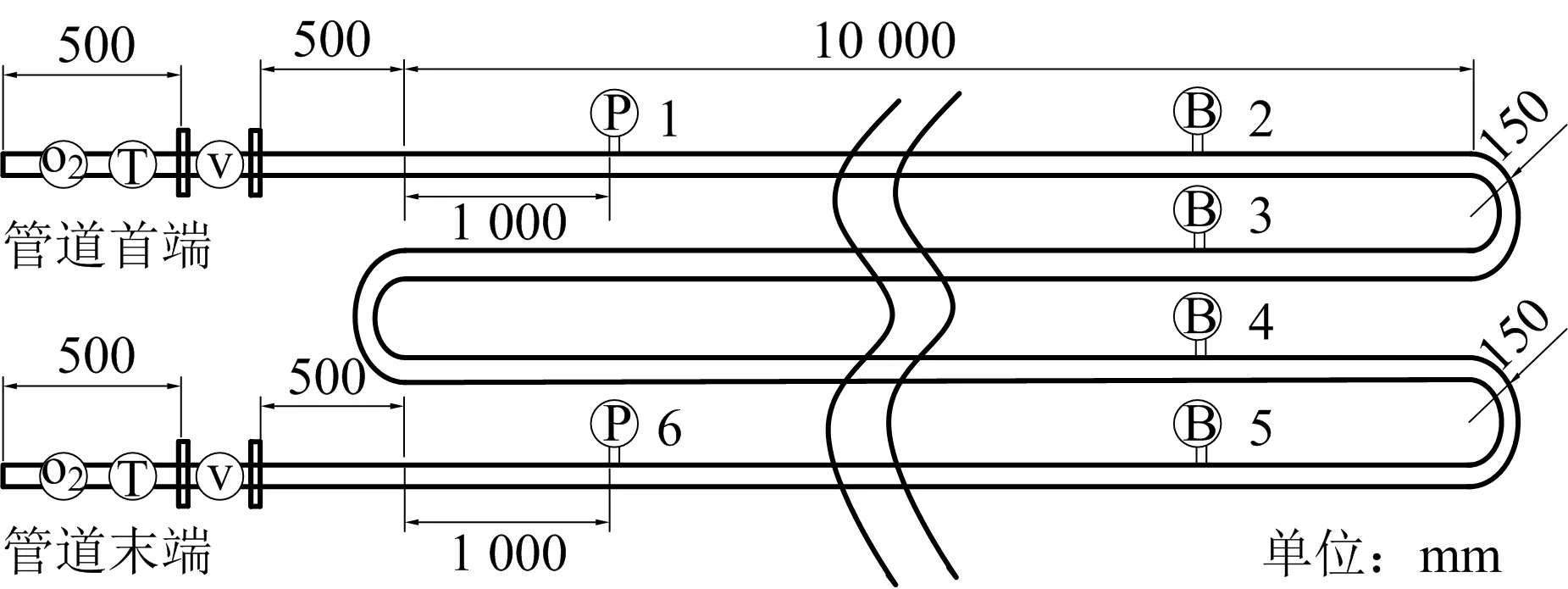
图4 瓦斯抽采管路实验系统Fig.4 Experimental system of gas drainage pipeline

2.2 实验步骤

1)检验实验装置气密性。在《瓦斯抽放管路的敷设规定》中要求，凡是新安装的瓦斯抽采管路，必须进行气密性测试，千米漏气不高于3 m3·min-1。

2)计算理论局部摩阻系数并修正系数。由于管道工况复杂，理论摩阻系数与实际有偏差，可以根据公式(1)及公式λ=kζ计算修正系数k和平均流量Q的关系，从而进行修正。

3)验证模型准确性。运用本文模型解算管道沿程压力，并与实验测量压力对比，从而验证元胞自动机模型准确性。

4)漏点定位及算法定位精度比较。设置泄漏点，分别利用元胞自动机模型、等温定位法和压力梯度法进行漏点定位，并进行不同算法的定位精度比较。

2.3 实验结果及分析

2.3.1 管道气密性检测

搭建实验平台，管道连接好后，进行气密性实验，随时间变化管道内压力如图5所示。

图5 管道内压力随时间变化示意Fig.5 Schematic diagram of pressure variation with time in pipeline

管道内初始压力P1=0.45 MPa，气体体积为管道体积V1，t=16 min后管道内压力P2=0.11 MPa，管道体积与泄漏出去的气体体积之和为V2。管道全长l=42 m，管道直径D=0.025 4 m。设管道每分钟千米漏气为ΔV，m3·min-1·km-1，根据公式PV=nRT可得：

(7)

计算可得ΔV=0.1 m3·min-1·km-1，千米漏气不高于3 m3·min-1，则气密性满足要求。

2.3.2 模型验证

为了验证元胞自动机模型的准确性，在模拟口2，3，4，5处安装量程为-60～0 kPa的压力变送器作为压力测点，测定管道内气体平均流量Q为22 m3/h时管道首末端压力参数PH，PE，如图6所示。根据检测的首端压力PH和流量Q，利用本文模型可得管道从首端到末端的沿程压力分布；同样根据检测的末端压力PE和流量Q，利用本文模型可得管道从末端到首端的沿程压力分布。

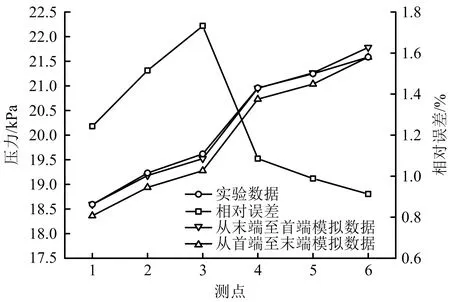
图6 Q=22 m3/h时CA模型解算压力值与实验检测压力值的比较Fig.6 Comparison of calculated pressure values of CA model with experimental detected pressure values at Q=22 m3/h

由于只在测点2，3，4，5处进行了模拟解算，故测点1，6处的压力作为始末点不计入结果中。最大误差值为测点2处的误差，仅为1.19%，其余误差均小于1%，误差平均值为0.88%。由此可见，CA模型的模拟解算结果与实验检测结果基本一致，误差较小，模拟结果理想。

2.3.3 漏点定位及算法比较

根据步骤(4)可得测点2泄漏前后的压力流量参数，如图7所示。

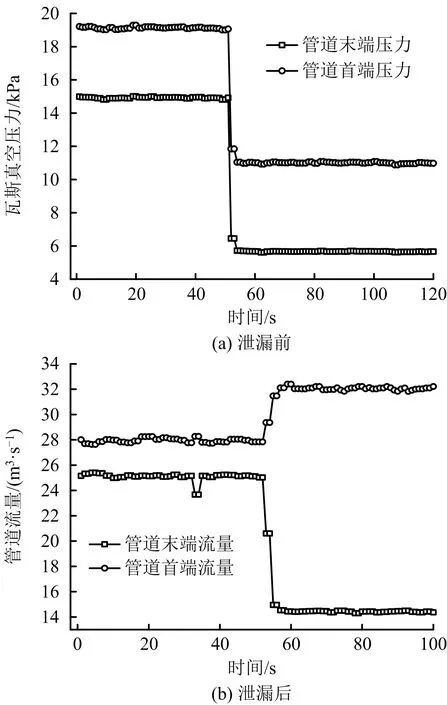
图7 测点2泄漏前后的压力流量参数Fig.7 Parameters of pressure and flow rate before and after leakage at No.2 measuring point

1)元胞自动机模型(CA)

运用本文所建立的元胞自动机模型进行漏点定位，进行解算可得从管道首端到末端的压力和从管道末端到首端的压力；绘制压力曲线可得图8(a)，交点横坐标x即为漏点位置。定位精度为|x-8|/L×100%。

2)等温定位法(LKA)

该方法将管道中气体流动视为等温过程且管道平均摩阻系数为常数§。管内稳态流动关系为 (PH2-PE2)/G2ZRT-2ln(PH/PE)=§L/D。绘制压力曲线可得图8(b)。

3)压力梯度法(PGA)

该方法假设管道流体为稳定流动，且压力分布为斜直线。当泄漏发生时，漏点前的流量变大，对应的压力分布直线斜率变大，而漏点后流量变小，相应直线斜率变小，由此可以确定该折点即为泄漏点。绘制压力曲线可得图8(c)。

图8 3种算法压力曲线Fig.8 Pressure curves of three algorithms

测点2，3，4泄漏发生后同样可以利用上述3种方法进行定位。最终测点2，3，4，5分别发生泄漏后，得到3种算法定位精度(见图9)。

图9 3种算法定位精度Fig.9 Positioning accuracy of three algorithms

由图9可知，CA模型的最大、最小误差分别为6.45%，2.06%，LKA和PGA的最大、最小误差分别为11.78%，3.78%和18.21%，7.53%。由此可见CA模型的定位精度在任何一处泄漏点的定位精度误差最小，LKA模型由于将管道平均摩阻系数等参数视为常数，过度简化模型导致误差增大，而PGA模型假设了管道流体为稳定流动，压力分布为直线，将模型理想化，导致模型误差最大。CA模型是由管道参数离散化后搭建的模型，在保证较小误差的前提下简化了计算，是3种算法中定位精度最为准确的一种算法。