细尾矿砂非饱和渗流稳态含水率二维解析解*

林雪松, 王永吉, 王 东, 王来贵, 王汉勍, 宋泽友, 王中东, 李俊岑, 冯 欢

(1.辽宁工程技术大学 理学院，辽宁 阜新 123000; 2.阜新高等专科学校，辽宁 阜新 123000;3.辽宁工程技术大学 力学与工程学院，辽宁 阜新 123000)

0 引言

尾矿坝一旦发生溃坝将对下游人民的生命安全和生存环境造成严重破坏[1]，因此一直以来都是安全生产领域的重点研究内容。近年来，由于尾矿颗粒越来越细[2]，固结越来越困难，坝体溃决概率出现了不断上升的趋势，使得针对细尾矿砂堆筑的尾矿坝的研究开始吸引学者们的注意[3-4]。水的分布状态是影响尾矿坝安全的重要因素，细尾矿砂堆筑的尾矿坝更是如此。尾矿坝中的水分有很大一部分是存在于非饱和尾矿砂中的，在尾矿坝的安全状态评估中，必须考虑非饱和部分的影响[5]，而清楚地描述非饱和尾矿砂内部水分的分布状况是考虑该部分影响的重要前提，必须进行深入探索。多年来国内外学者针对非饱和渗流问题进行过很多有意义的研究。张志军等[6]通过尾矿砂室内毛细水上升测试发现：尾矿砂中毛细水的上升规律呈初期迅速而后期缓慢的变化趋势，是其受多种作用力的共同作用所致;魏样等[7]通过室内土柱试验发现：不同土质的污染土壤内，毛细水上升高度与时间均符合良好的幂函数关系;郝瑞等[8]利用自行设计的层状土室内模型试验监测了毛细水上升过程，通过试验结果对LW模型进行了修正。前述工作可归类为实验方面的研究，在数值计算方面，Neuman[9]首先提出通过有限元方法解决二维饱和-非饱和渗流问题;汤卓等[10]基于非饱和土渗流理论建立了尾矿坝三维有限元模型，总结了上游法尾矿坝流固耦合计算规律；彭华等[11]对渗流问题的有限元分析方法加以改进，消除了非饱和渗流计算中存在的数值弥散现象，提高了收敛速度 ;王铁行[12]给出了考虑含水率和密度影响的非饱和黄土路基水分场数值计算模型;刘杰等[13]研究了非饱和土路基毛细作用的数值与解析方法;李毅等[14]运用变单元渗透系数法，通过FLAC3D的二次开发得到了饱和-非饱和渗流场;王睿等[15]通过引入时间分数阶导数，结合2种水力传导系数对新的Richards方程进行了数值求解。

纵上发现，前人在非饱和渗流问题的实验和数值计算方面进行了大量研究，但较少见到解析方法方面的研究，即便使用解析方法也仅限于处理一维问题。实验和数值计算当然是探讨非饱和渗流问题的有效方法，应该投入精力进行研究与发展，但重视实验和数值方法的同时也应该重视解析方法，加之尾矿坝问题通常涉及2个维度，因此对二维问题的解析研究意义也同样明显。

本文拟从非饱和渗流的Richards方程出发，在对求解区域和边界进行适当加工的基础上，得到尾矿砂二维非饱和渗流的稳态解析解，然后通过得到的解析解拟合细尾矿砂实验数据，观察解的拟合效果。主要目的是通过研究给出符合实际的非饱和细尾矿砂内含水率分布计算的思路与方法，为考虑非饱和部分的尾矿坝安全评估工作提供基础资料。

1 创建解析模型

Richards方程是细尾矿砂非饱和渗流所涉及的基本方程，若以体积含水率θ为待求解函数，坐标系的z轴以竖直向上为正，三维问题中的Richards方程的形式如式(1)所示[16]。方程中的D(θ)称为扩散系数，D(θ)随θ的变化而变化，因此表达为函数形式；K(θ)表示非饱和尾矿砂中水分的渗透系数，也表达成了θ的函数。在尾矿坝工程中通常研究的都是二维问题，此情况下，如将坐标轴y以竖直向上为正方向，且仅仅研究稳态问题不讨论瞬态问题，式(1)可变化为式(2)。虽然式(2)的形式已经比较简单，但若想求得解析解尚需在符合实际的基础上继续简化。接下来将D(θ)取为常数D，则式(2)又可化为式(3)。

(1)

(2)

(3)

需要指出的是，将D(θ)取为常数D并不是认为实际中D(θ)一定为常数，而是在运算中用某种平均值来代替D(θ)，前人曾实践过类似的简化思路[13]。式(3)必须和一定的求解区域和边界条件联系在一起才能求解，若区域的形状太过复杂是无法得到解析解的，因此应当将求解区域选为简单形状，在接下来的研究中，选择矩形求解区域，因为矩形区域内的方程求解是完全可以做到的，且实际中很多工程问题的求解也可归结到矩形区域内。接下来考虑式(3)的边界条件。通过对已有实验结果(论文后面会给出)的分析可看出，含水率在竖直和水平方向上都近似遵循指数变化的规律，有鉴于此，在矩形的求解区域内，建立式(4)～(6)所示的方程和边界条件。

(4)

θ|x=0=ae-byθ|x=q=ce-dy

(5)

θ|y=0=fe-gxθ|y=h=je-kx

(6)

2 求解模型的具体过程

方程和边界条件建立起来之后，就涉及到求解整个模型。首先，方程和边界条件都是非齐次的，可对边界条件先进行齐次化处理。令含水率θ=w+v，w和v为2个待定函数。假设v满足边界条件(5)，且令v=Ax+B，A和B同样为2个待定函数。将v带入边界条件(5)解得：

(7)

从v的表达式中可看出：

(8)

将θ=w+v及v的表达式带入方程和边界条件(4)～(6)得到关于w的方程和边界条件如式(9)～(11)所示：

(9)

w|x=0=0，w|x=q=0

(10)

(11)

利用分离变量和傅立叶级数法可得到w的表达式为：

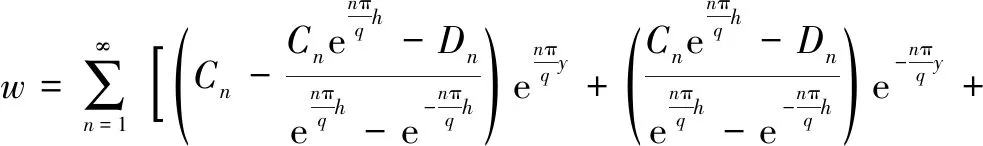
(12)

公式中Cn，Dn的形式为：

(13)

(14)

则最终得到含水率空间分布的表达式为：

(15)

很明显最终的结果具有无穷级数形式，但由于系数都具有很强的收敛性，所以在实际中只取其中前几项就足够了。

3 基于实验结果的模型效果检验

3.1 实验设计与结果

1)实验装置与物料

主要实验装置如图1所示，包括储水腔室(1 m×0.1 m×1 m)和储料腔室(0.1 m×0.1 m×1 m)，尾矿物料全部放置在储料腔室内，图1中储料腔室上的格点表示计划测含水率的位置。储水腔室用于提供渗流过程中所需的水，2个腔室之间的隔板上设置有钻孔，用来保证渗流过程中水供应的顺畅。实验对象为某铁矿尾矿砂，颗粒组成见表1，表1中数据显示：50%以上颗粒粒径小于0.019 mm，大于0.074 mm的颗粒含量低于10%，大于0.037 mm的颗粒含量低于30%，实验用尾矿砂完全可归类于细尾矿砂[17-18]。或者按照工程分类方式归类为尾黏土。

2)实验主要过程与参数设定

在实验开始之前，先将尾矿砂填筑到储料腔室内，然后在储水腔室中注入清水，当腔室内水位达到0.05 m时停止注水，并通过虹吸方式使水位保持恒定。接下来细尾矿砂开始在恒定水源水位的基础上进行饱-非饱和渗流。实验中润锋的位置与形态不断发生变化，当润锋完全稳定时认为实验结束。细尾矿砂渗流速度较慢，从实验开始到润锋稳定共计用了2个月时间。刚开始水平向渗流速度大于竖直向渗流速度很多，但随着渗流的发展二者差距越来越小。稳定后的状态如图1所示，图1中AA′表示稳定后的润锋，BB′表示实验中尾矿砂试件内出现的1个裂缝。渗流达到稳态后对储料腔室上标记的各格点进行挖掘，利用烘干法测含水率。该细尾矿砂饱和状态体积含水率为49.80%。

表1 细粒尾矿砂粒径组成Table 1 Composition of particle size of fine tailing sand

图1 实验结果Fig.1 Experimental results

3)实验结果

测量得到的竖直向含水率分布曲线如图2所示，水平向含水率分布曲线如图3中的实测值所示。由图2～3可知：无论竖直还是水平方向，含水率均逐渐降低，降低趋势具明显的非线性，可近似用指数函数描述。鉴于曲线的分布特点，前述模型中的边界条件均采用指数形式。

图3 水平向含水率分布Fig.3 Horizontal distribution of water content

3.2 模型参数的确定

前述解析解(15)中包含共计10个未知参数，未知参数完全可利用实验数据通过数学方法得出。可选的数学方法有很多，通过仔细调研，最终决定采用混沌粒子群优化算法(Chaos Particle Swarm Optimization，CPSO)来计算参数。由于理论公式只能应用在矩形区域内，因此应用公式的时候首先需要构造矩形域。

为检验计算得到的参数对所有数据的预测结果如何，需将由理论模型计算得到的各点含水率与实际测量结果进行比较，接下来展示出不同高度处含水率沿水平方向分布的实测值和理论值，以此将所有测量点处的实际测量值与理论计算值进行比较。比较结果如图3所示。如果仔细观察图3可看出，在高度0.1，0.3和0.4 m处，实测值与计算值符合的比较好，在高度0和0.2 m处，数据拟合结果相对要稍差一些，但相差的也不是很大，总体来说，模型计算值和实测值是比较接近的，证明了用推导出的公式来描述实验数据是完全可行的。因此解析解可被认为是含水率空间分布的理论规律，计算得到的分布曲线一般是要比测量得到的曲线稍显平滑。

3.3 拟合结果

针对3.1节实验构造的矩形域如图1中的COEF所示，在矩形域上分别建立了x轴和y轴，矩形域内共计包含了50个数据点，可用来拟合参数。运算中在参考试算经验的基础上，将最大迭代次数设置为1 000，迭代过程中误差的变化如图4所示，从图4中看到，开始的时候收敛速度比较快，然后收敛速度逐渐变慢，随着迭代次数的增加最后误差趋于恒定值。由计算得到公式中的未知参数取值如下：

α=6.839 088 379,β=20 000.0,a=44.229 302 31,b=0.096 026 944 5,c=979.961 319 9,d=20 000.0，f=4 465.811 49,g=0.120 477 598 5,j=21.483 476 85,k=16 768.464 75,D=16 177.809 65。

图4 误差变化Fig.4 Error development

4 结论

1)通过解析方法得到了描述非饱和尾矿砂含水率空间分布的公式，求解过程表明，细尾矿砂非饱和渗流稳态问题的解析求解可以从Richards方程的简化开始，简化主要沿着2个方向，第1是将方程形式简化，简化过程中包括降低维度，变瞬态为稳态，将未知参数简化为常数或固定函数形式等；第2是将复杂求解区域简化为矩形，在矩形区域里只要给出合适的边界条件是可以得到方程解析解的。

2)模型求解所需的边界条件可在参考实验数据的基础上给出，以此来保证求解结果的有效性。简化过程中引入的参数可通过CPSO算法编制程序利用测量数据得出。算法计算中误差具有明显的收敛性。得出的参数能够很好地拟合全部测量数据。由计算得到的曲线较实测曲线具有明显的光滑性。