跨江泥水盾构掘进过程中的沿江路段地表变形特征

李军，黄帅，黄林冲，梁禹



跨江泥水盾构掘进过程中的沿江路段地表变形特征

李军1，黄帅2，黄林冲2，梁禹2

(1. 广东省水利电力勘测设计研究院，广东 广州 510635；2. 中山大学 工学院，广东 广州 510275)

为研究盾构隧道施工对地表变形的影响，以某过江盾构隧道沿江大道段的施工为背景，通过对现场监测数据以及施工过程的分析得出地表变形规律及其成因，结合三维有限元模拟该段盾构施工，并与实测值进行对比，根据分析结果以及工程实践提出盾构施工地表变形控制措施。研究结果表明：施工过程中泥水压力对地表沉降影响显著；实际盾构掘进过程中引起的地表横向变形分布表现为隆起变形，且与传统Peck沉降曲线存在区别，纵向地表变形整体表现为先沉降后隆起的趋势，在掘进过程中应调整泥水压力控制地表变形；隧道有限元模型模拟结果与监测数据趋势一致，在有针对性的工程措施保证地表变形值总体可控。

泥水压力；地表变形；盾构隧道；有限元模拟；监测分析

盾构工法具有施工效率高、机械化程度高及对周围环境影响小等优点，在越江隧道工程中有广泛的应用[1−2]。在施工期间不可避免地会产生地层损失，引起地层变形及地面沉降，如何预测施工引起的地层位移，确保附近建筑物的结构安全，是盾构法隧道设计及施工过程中需要解决的重要问题[3]。盾构法在掘进施工过程中会对地层产生扰动，从而改变了土体的初始应力，使周围地层发生变形，盾构掘进对地层的扰动以及掘进参数的设置直接影响纵向地表变形[4]。国内外对于盾构施工引起的地表沉降的研究大致可归纳为[5]：经验公式法、随机介质法、数值计算法、模型实验法和现场监测法。DING等[6]提出在建筑物作用下、扰动范围内和扰动范围外，地表沉降分别呈现出软木分布曲线特征、斜交分布曲线特征和正态分布曲线特征；魏纲等[7]建立修正的随机介质理论简化计算公式预测盾构施工引起的地表沉降；邓宗伟等[8]基于流固耦合原理通过FLAC3D建立盾构隧道施工模型研究泥水参数对于地表沉降的影响；马险峰等[9]利用离心模型试验对盾构隧道的地层损失进行了模拟，研究了地层损失与施工期及施工后纵向地表沉降的关系；谢雄耀等[10]开发了沉降自动化监测及数据移动发布系统，从而实现监测数据的自动化实时采集、分析和移动端推送，通过分析结果优化施工参数。本文以某过江盾构隧道工程为研究对象，通过在沿江大道段布设测点，对盾构隧道下穿沿江大道的现场及后期施工阶段进行了地表沉降的监测，通过现场监测结果分析了其地表变形规律及成因，结合实际工程建立了三维盾构施工有限元模型，并将数值分析结果与现场监测结果进行对比，分析研究盾构施工过程中泥水压力对横向地表变形和纵向地表变形的影响，最后根据分析结果和工程实践提出地表变形控制措施。

1 工程概况及现场监测

1.1 工程概况

某越江隧道采用泥水盾构法施工，隧道过江段采用双管单层型式，分为南北2线越江，北线先施工，本文取北线下穿过沿江大道段进行分析。管片外径11.3 m，管片内径10.3 m，管片厚度50 cm，环宽2 m。隧道穿越的地层条件主要有杂填土、强风化砾岩和中风化砾岩，本文选取的隧道段主要处于强风化砾岩层中。越江隧道江中盾构段自东岸始发井始发，逐渐往西延伸，首先经过现有围蔽施工场地，再横穿沿江大道，而后下穿沿江大堤，盾构隧道由东往西越江，本文主要研究盾构隧道下穿沿江大道引起的地表变形。

1.2 现场监测分析

盾构隧道横穿沿江大道，盾构施工对地层的扰动引起地表变形，影响着沿江大道的正常运行。为保证沿江大道结构安全，本文主要选取NK1+760~ NK1+640段布置测点(S1~S9)进行地表变形值进行分析。其监测点布置情况如图1所示，其中断面NK1+700与NK1+650处测点主要监测沿江大道处横断面地表变形分析。本文研究的过江隧道盾构施工主要分为2个阶段：NK1+760~NK1+710为试验段，在此过程中对各项掘进参数进行调整，盾构掘进施工时，泥水仓压力设置较大(2.1~2.4 bar)；NK1+710~NK1+640为正常掘进段，泥水仓压力设置小于试验段掘进时的泥水仓压力(1.3~1.8 bar)。

图1 地表变形监测点布置平面图

对典型断面NK1+700和NK1+650进行了连续监测，图2为NK1+700处监测点测得的横断面地表隆沉变形。从图2可以看出，当刀盘掘进至距断面−10 m时，断面总体呈现隆起变形，中间大两边小，最大隆起值出现在测点S6-4为5.48 mm。在掘进面到达测点正下方时，各测点仍出现较小的隆起。最终稳定后监测断面地表测点S6-1产生最大沉降量−3.75 mm，S6-4产生最大隆起值为4.44 mm。均小于《盾构法隧道施工与验收规范》(GB50446—2008)等规范规定的变形控制值(10 mm)。NK1+700监测断面位于试验段前方仅10 m，经推断其地表隆起的原因主要是由于盾构在试验段掘进时泥水仓压力设置过大造成[11]。

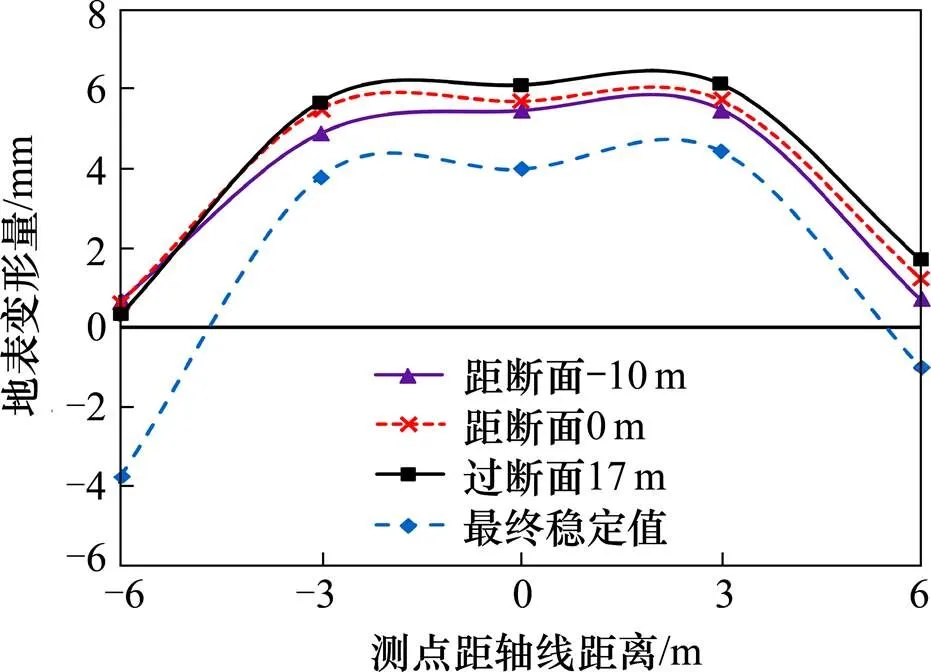
图2 NK1+700断面测点地表沉降随刀盘距离变化曲线

图3为NK1+650处监测点测得的横断面地表隆沉变形。从图3可以看出，除在S8-2测点测得有极微小的隆起以外，其余测点均为沉降变形。最终稳定后，监测断面地表测点S8-1测得最大沉降量1.02 mm。NK1+650断面位于盾构正常掘进段，其泥水压力与地层侧向压力基本处于动态平衡状态，因此该地段地表变形较小。图3地表沉降曲线并非关于隧道中心线对称，主要是因为该断面并非均一地层，属于粉质黏土层与强风化砾岩地层的过渡段，岩性变化较大，此外地表沉降还受掘进参数、同步注浆、盾构姿态控制等影响，实测曲线与传统peck沉降曲线有差别。

图4为NK1+770-NK1+625纵向地表沉降与盾构机泥水压力变化图。从图4可以看出，纵向地表变形受泥水压力影响显著。掘进至断面NK1+710前为试验段，泥水压力较大；断面NK1+710之后为正常掘进段，泥水压力设置较小。尽管断面NK1+710前测得的泥水压力较大，但从现场施工情况来看，由于掘进时机器故障、参数调试、换刀等原因，盾构机停机频繁，在停机保压过程中，由于盾构机处于一个静态平衡的过程，泥水压力会在渗透压力作用下沿着地层裂隙流失，而达不到预设的保压平衡，当土体侧压力大于泥水平衡压力时，容易产生地表沉降[4]。

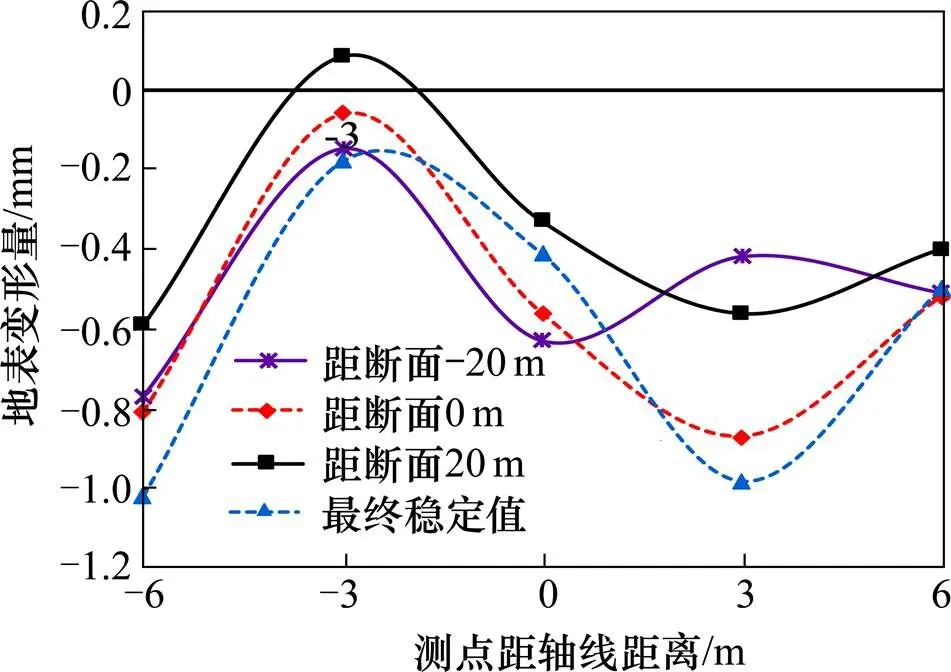
图3 NK1+650断面测点地表沉降随刀盘距离变化曲线

断面NK1+710之后，盾构机掘进参数调试回归正常，停机时间减少，盾构机运行平稳。从图4可知，盾构在正常段推进时泥水仓压力较试验段有所下降，但是在断面NK1+710附近的位置上地表变形发生突变，由沉降变形突变为隆起变形，结合施工实际分析其原因，盾构机在掘进至断面NK1+720环附近进行了停机调试，因此在该点附近地表沉降达到最大，最终沉降值为9.28 mm。之后开机启动，泥水仓重新建立动态泥水平衡，地表沉降量迅速减小直至发生隆起，至断面NK1+700达到最大，最终隆起值为3.98 mm。断面NK1+710附近泥水压力降低，随后地表隆起变形量逐渐减小。随着盾构机掘进，地表隆沉变形按一定趋势变化。在正式掘进段，地表隆起随着盾构机向前掘进逐渐减小。一般认为，地表变形趋势变化的原因是后期土层自身扰动及固结所引起，但无论是沉降还是隆起，其变形均较小。

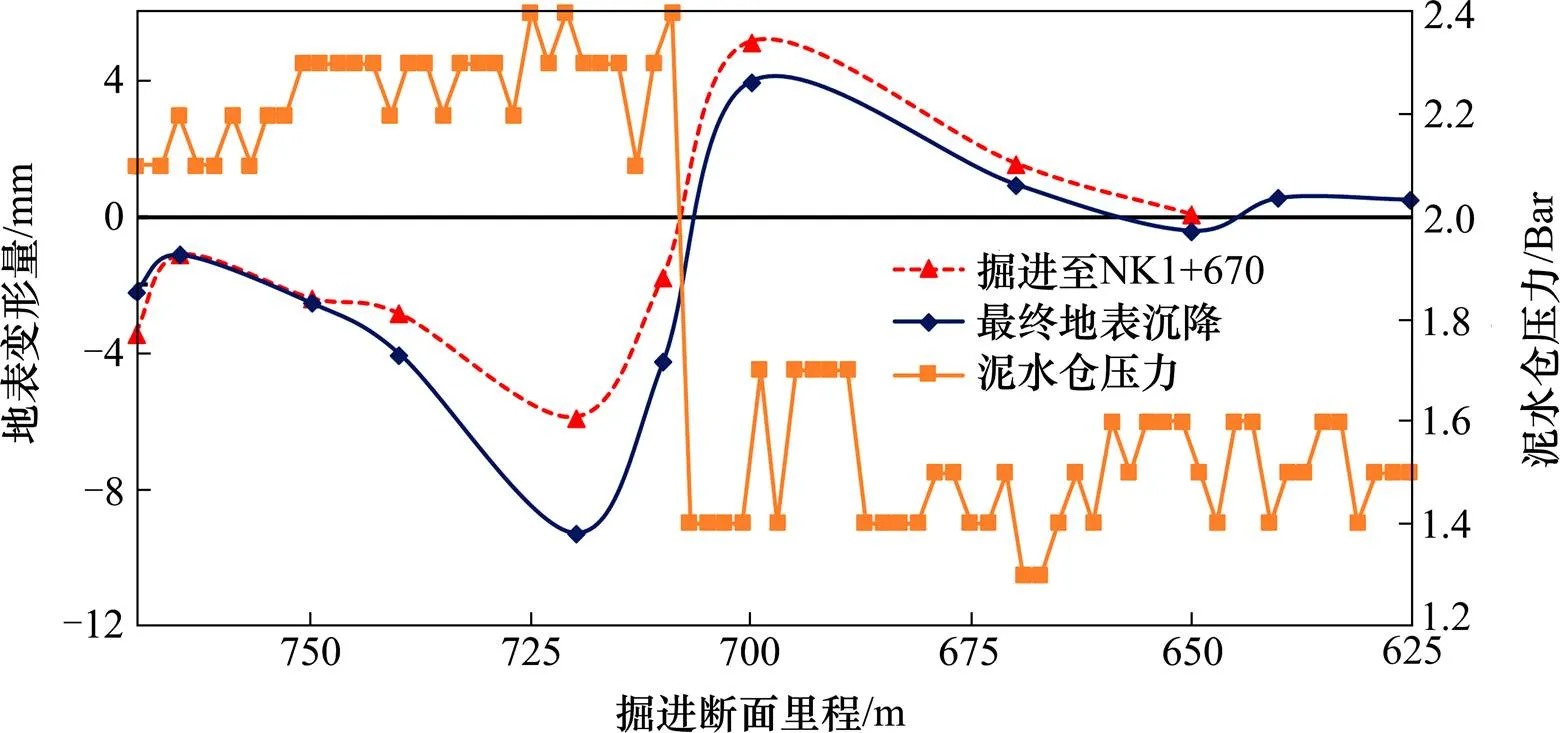
图4 纵向地表沉降与盾构机泥水压力变化图

2 数值模拟

为研究泥水压力对盾构引起地表变形的影响，本文建立有限元模型，按照实际施工情况设置不同泥水压力进行分析。

2.1 数值计算模型

本文采用有限元软件Midas GTS-NX建立该盾构隧道施工的三维有限元模型，选取实际断面NK1+760~NK1+640这段进行模拟分析，模型尺寸为120 m×120 m×70 m，如图5所示。隧道长度模拟为120 m，包括60环管片，沿江大道网格尺寸为1 m，土层网格尺寸为4 m，盾壳、管片、注浆层及开挖区域网格尺寸为1 m，隧道断面NK1+760向断面NK1+650进行开挖。沿江大道和各土层均简化为匀质水平层状分布，开挖步长为2 m，模拟开挖仅从空间推进，不考虑时间效应。模型设置地下水位(−5 m)，土层、沿江大道、注浆层均采用实体单元模拟，管片和盾壳则采用板单元进行模拟，模型边界条件为四周采用法向约束、底端采用固定约束。本模型模拟的荷载主要有：泥水压力、自重、注浆压力和盾壳前进过程中对管片的千斤顶力。模型划分为179 336个单元，105 222个节点。

土层计算参数如表1所示，隧道位于中风化砾岩层中。

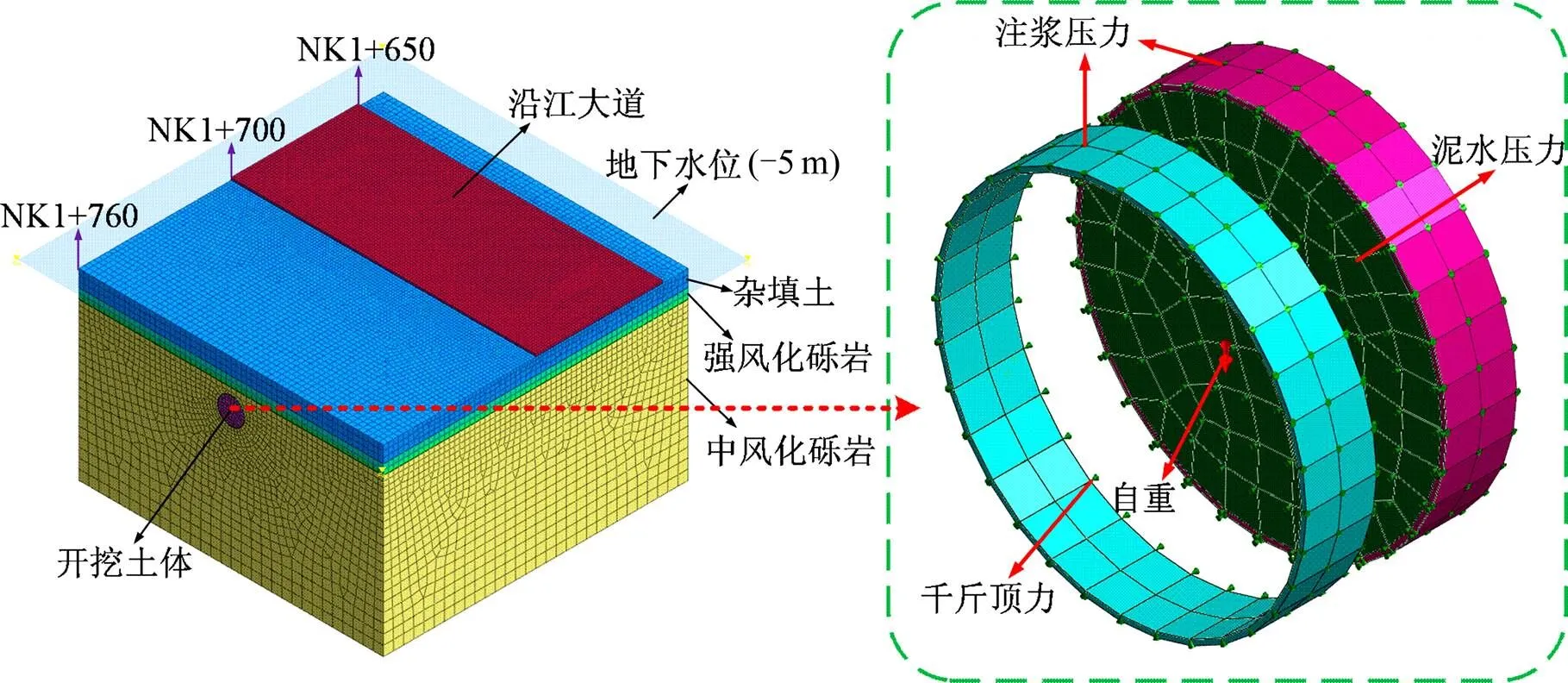
图5 有限元模型

表1 土层物理力学指标

2.2 计算结果分析

为研究盾构掘进过程中泥水压力变化对于地表变形的影响，本文考虑改变泥水压力及模拟盾构停机工况，模型施工步主要分为2个阶段：试验段施工和正常施工段。

1) 试验段施工模拟(断面NK1+760~NK1 +710)。第1个施工步向前掘进一环，泥水压力设置为240 kPa；第2个施工步掌子面不推进，仅将泥水压力降至100 kPa。直至掘进至断面NK1+710，共50个施工步，模拟试验段施工的频繁停机过程。

2) 正常施工段模拟(断面NK1+710~NK1+ 640)。施工步正常模拟，即每个施工步掌子面均向前掘进一环，共35个施工步，同时泥水压力设置为120 kPa，管片滞后一环安装。

2.2.1 地表变形横向分布规律

图6(a)和6(b)分别表示盾构刀盘到达断面NK1+700及NK1+650时沿江大道的竖向变形云图，从图中可以看出，当掘进至断面NK1+700时，隧道掌子面正上方各测点(S6-1~S6-5)位置表现为隆起变形，沿隧道中轴线呈对称分布，最大隆起值为1.78 mm。隆起现象主要由于试验段盾构施工时，掌子面施加的泥水压力较大(240 kPa)，挤压前方土体，造成前方地表发生隆起变形。当盾构刀盘到达断面NK1+650时，隧道掌子面正上方各测点(S8-1~ S8-5)位置表现为沉降变形，最大沉降位于隧道中轴线对应的地表测点(S8-3)，其沉降量为1.88 mm，分析其原因，主要是断面NK1+650距离试验段较远，所受的影响小，其泥水压力相对设置较小(120 kPa)，断面上方土体由于隧道开挖引起地层损失，地表测点出现沉降变形。

(a) NK1+700；(b) NK1+650

为研究在盾构隧道开挖推进过程中地表的横向沉降整体变化规律，以2个典型断面(NK1+700和NK1+650)为研究对象，通过研究2断面对应测点地表沉降曲线在盾构开挖掘进中的变化情况，得出其变化规律。并结合实测数据进行比对，结果如图7所示。从图7(a)中可以看出：掘进至断面NK1+ 700时，该断面上测点的实测值与模拟值的趋势一致，均为隆起变形，两端测点的模拟值与实测值十分吻合，中间测点模拟值小于实测值，这是由于实际施工环境更为复杂所致。同时比较图中掘进至不同断面时得到的地表横向变形曲线，随盾构施工的推进，其横向隆起变形减小，并逐渐转化为沉降变形，分析其原因，这是由于断面NK1+710后为正常施工阶段，其泥水压力设置较小，对前方土体的挤压作较小，从而隆起变形量减小，隧道继续开挖施工造成上方土体地层损失导致后期产生地表沉降。图7(b)中模拟值与实测值虽趋势有所差异，其原因在于断面NK1+650实际的地层条件更为复杂，而模拟采用的是均以地层条件，但由于该断面的泥水压力设置较小，其地表变形呈现沉降，且变形量与实测值较为接近，地表横向沉降槽随盾构的推进而逐渐加深。基于以上分析可以得出：泥水压力过大会导致地表产生隆起变形，通过实时改变泥水压力可以有效的控制地表变形。

(a) NK1+700；(b) NK1+650

2.2.2 地表变形纵向分布规律

选取隧道中轴线正上方地表变形进行分析，图7为纵向地表变形随盾构掘进的变化曲线，并结合掘进至断面NK1+670时的实测数据进行对比分析。从图8可以看出：掘进至断面NK1+670时，其有限元模拟得出的结果与实测结果趋势一致，说明了该模型参数的设置基本满足需求。模拟值总体较实测值偏小，模拟的最大隆起变形量为0.5 mm，最大沉降量为5.5mm。这是由于模型只模拟泥水压力变化对地表变形的影响，而未考虑孔隙水压力、同步注浆等因素。断面NK1+710之前，由于模拟了频繁停机过程，各测点地标变形模拟值与实测值一致，均表现为沉降变形。模拟的最大沉降至出现在开始掘进的断面(NK1+760)，与实测不同，其最大沉降值出现在断面NK1+720处，这是由于模型边界所致。模拟值在断面NK1+720处也出现了较小的沉降趋势，这说明了模拟的盾构施工试验段能很好的描述实际工况。模拟结果在断面NK1+710之后也先后出现了较小的隆起变形，与实际结果趋势一致，但隆起变形量小于实测值。对比掘进至不同断面的地表纵向变形的曲线，可以看出：其整体趋势相同，沿着隧道中轴线上的测点，地表均是由沉降变形逐渐转变为隆起变形，且隆起变形量远小于沉降变形量。由沉降变形突变为隆起变形的位置随着盾构施工的掘进而逐渐向施工前进方向移动，地表变形量差值随施工方向现增大后减小，最大差值出现在断面NK1+720的位置。模拟结果表明地表变形受泥水压力影响较大，盾构停工保压过程中如泥水压力设置过小会导致地表出现沉降变形。

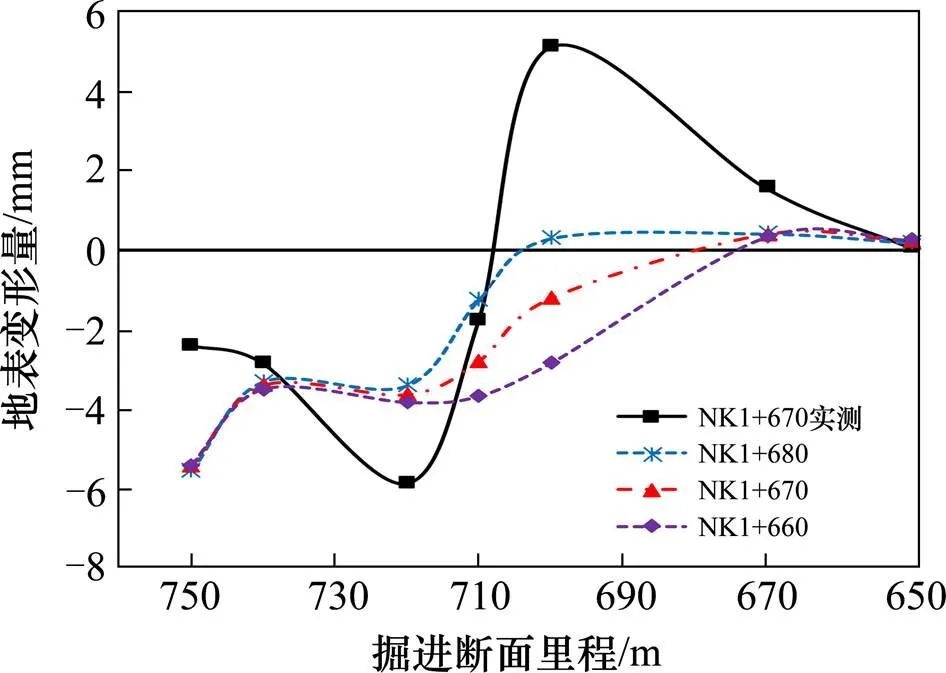
图8 掘进至断面NK1+670地表纵向变形

3 地表变形控制措施

盾构施工时应不断优化各施工参数，并使各参数相匹配，使其对周围地层影响最小。基于工程实践提出以下有针对性的地表变形控制措施。

1) 泥水压力、泥浆流量及质量的控制[12]。因覆土厚度不断变化，泥水压力难以及时调节，为避免泥水压力过小导致开挖面土体失稳，建议基于隧道最大埋深设定泥水压力。当开挖面土层以黏性土为主时，黏土易结块，泥水舱及泥浆泵易堵塞，为避免堵塞引起泥水压力波动，应加大进出泥浆流量，提高泥浆携带土块的能力。

2) 同步注浆及二次注浆控制。在盾构穿越施工时，掘进速度、刀盘转速控制平稳，尽量做到匀速、不间断通过，以减小对地层的扰动，实现在地层产生较大变形之前迅速完成同步注浆及二次补注浆作业，及吋补充地层损失，从而减小土体变形。

3) 盾构掘进速度及姿态控制。在保证开挖面稳定的前提下，尽可能快速地通过沿江大道，并避免盾构较长时间的搁置；推进轴线尽量与隧道轴线保持一致，减小纠偏量，减轻盾构与周围土层之间的摩擦。南线在根据北线先期施工经验调整施工参数后，其中掘进速度的调整情况如图9所示，南线掘进速度明显大于北线，由两线实测数据对比可知南线地表变形小于北线。

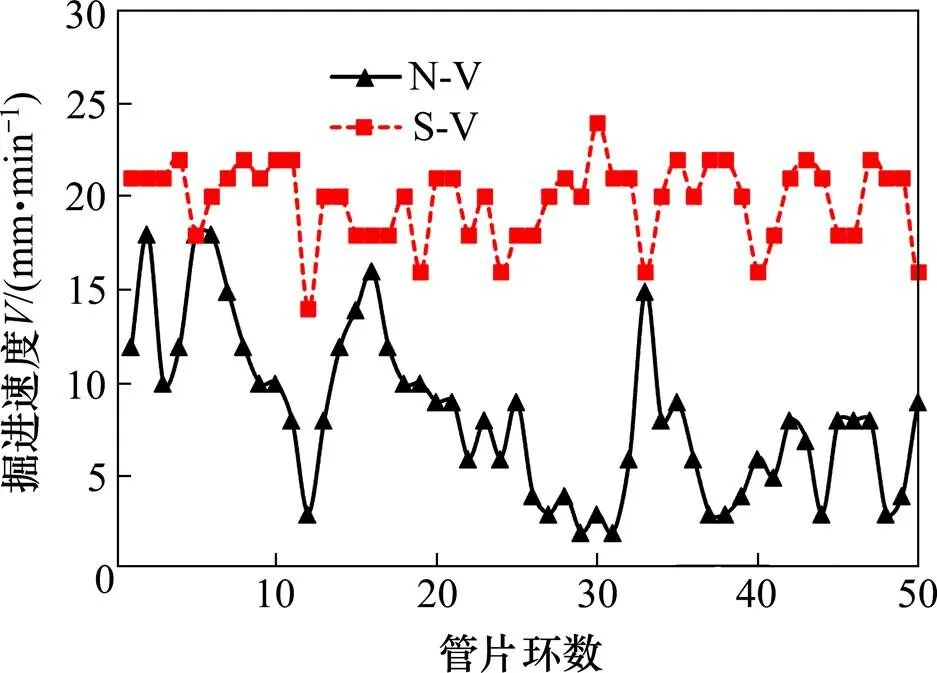
图9 南北线掘进速度变化曲线

4) 在沿江路段上布置合理的监测点位，加大监测频率，密切关注地表沉降情况，根据监测结果实时优化掘进参数。

5) 盾构穿越后的处理。在盾构穿越后，仍需长期监测，掌握沿江路段的沉降状况，沉降监测应持续到沉降稳定为止。

4 结论

1) 盾构隧道掘进引起的地表横向沉降分布曲线形态和经典Peck沉降曲线有一定差别，断面NK1+700呈现明显的隆起变形。主要是因为在断面NK1+700前方为盾构试验段，其泥水压力设置过大，大于土体侧压力使被测断面产生隆起变形。断面NK1+650随盾构掌子面推进基本表现为沉降变形，但并非关于隧道中心线对称，这主要由于地层不均一岩性变化较大所致。

2) 盾构隧道施工引起的纵向变形最大隆起值为3.98 mm，最大沉降值为9.28 mm。由监测结果可知，地表隆起和沉降变化主要受泥水压力变化影响。泥水压力在盾构机停机保压过程中会沿地层裂隙往外渗透流失，从而导致掌子面难以处于保压平衡状态，当土体侧压力大于泥水平衡压力时，容易产生地表沉降。盾构机突然启动，重新建立掌子面动态平衡后，在较大泥水压力作用下，刀盘前方土体又产生隆起变形。

3) 通过有限元软件Midas GTS-NX对该区间段施工进行模拟，模拟过程采用不同掘进压力拟合实际施工情况。盾构通过断面NK1+700表现为隆起变形，断面NK1+650呈现沉降变形，最大值都出现在隧道中心线位置，纵向地表变形曲线趋势与实测结果基本一致。对比数值分析的结果和现场监测数据分析，得到了地表隆沉变形随盾构泥水压力变化的趋势。

4) 结合过江隧道穿越沿江路段的现场监测结果以及针对该工程的数值模拟结果分析得出：本工程中影响地表变形的因素主要是泥水仓压力的变化。在沿江大道上布置合理的监测点位，并加大监测频率，时刻关注沿江大道地表变形情况，根据监测结果实时调整优化掘进参数，尤其泥水仓压力，防止其设置过大导致地表隆起量过大。结合数值分析、现场监测与工程实践，提出合理的施工控制措施，优化掘进参数，减小盾构掘进对地表沉降的 影响。

[1] 梁禹, 阳军生, 王树英, 等. 考虑时变性影响的盾构壁后注浆浆液固结及消散机制研究[J]. 岩土力学, 2015(12): 3373−3380. LIANG Yu, YANG Junsheng, WANG Shuying, et al. A study on grout consolidation and dissipation mechanism during shield backfilled grouting with considering time effect[J]. Rock and Soil Mechanics, 2015(12): 3373− 3380.

[2] 梁禹, 阳军生, 林辉. 大直径盾构隧道施工阶段管片上浮与受力研究[J]. 现代隧道技术, 2016, 53(3): 91−97. LIANG Yu, YANG Junsheng, LIN Hui. On segment floating and relevant mechanical behaviors during large-diameter shield tunnelling[J]. Modern Tunnelling Technology, 2016, 53(3): 91−97.

[3] GAO M Z, ZHANG Z L, QIU Z Q, et al. The mechanism of hysteretic ground settlement caused by shield tunneling in mixed-face conditions[J]. Geomechanics and Geophysics for Geo-Energy and Geo-Resources, 2017(3): 1−11.

[4] ZHU C. Control of surface settlement by considering shield tunneling technology[J]. Ksce Journal of Civil Engineering, 2017, 21(7): 2896−2907.

[5] 叶飞, 苟长飞, 陈治, 等. 盾构隧道同步注浆引起的地表变形分析[J]. 岩土工程学报, 2014, 36(4): 618−624. YE Fei, GOU Changfei, CHEN Zhi, et al. Ground surface deformation caused by synchronous grouting of shield tunnels[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(4): 618−624.

[6] DING Z, WEI X J, WEI G. Prediction methods on tunnel-excavation induced surface settlement around adjacent building[J]. Geomechanics & Engineering, 2017, 12(2): 185−195.

[7] 魏纲, 周杨侃. 随机介质理论预测近距离平行盾构引起的地表沉降[J]. 岩土力学, 2016(增2): 113−119. WEI Gang, ZHOU Yangkan. A simplified method for predicting ground settlement caused by adjacent parallel twin shield tunnel construction based on stochastic medium theory[J]. Rock & Soil Mechanics, 2016(Suppl 2): 113−119.

[8] 邓宗伟, 伍振志, 曹浩, 等. 基于流固耦合的泥水盾构隧道施工引发地表变形[J]. 中南大学学报(自然科学版), 2013, 44(2): 785−791. DENG Zongwei, WU Zhenzhi, CAO Hao, et al. Surface deformation of slurry shield tunneling using fluid-solid coupling theory[J]. Journal of Central South University (Natural Science), 2013, 44(2): 785−791.

[9] 马险峰, 王俊淞, 李削云, 等. 盾构隧道引起地层损失和地表沉降的离心模型试验研究[J]. 岩土工程学报, 2012, 34(5): 942−947. MA Xianfeng, WANG Junsong, LI Xiaoyun, et al. Centrifuge modeling of ground loss and settlement caused by shield tunnelling in soft ground[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(5): 942− 947.

[10] 谢雄耀, 李军, 王强. 盾构施工地表沉降自动化监测及数据移动发布系统[J]. 岩土力学, 2016(增2): 788−794. XIE Xiongyao, LI Jun, WANG Qiang. Automatic monitoring and mobile data publishing system of ground settlement induced by shield tunneling[J]. Rock & Soil Mechanics, 2016(Suppl 2): 788−794.

[11] FANG Y, HE C, Nazem A, et al. Surface settlement prediction for EPB shield tunneling in sandy ground[J]. Ksce Journal of Civil Engineering, 2017, 21(7): 2908− 2918.

[12] 张亚洲, 闵凡路, 孙涛, 等. 硬塑性黏土地层泥水盾构停机引起的地表塌陷机制研究[J]. 岩土力学, 2017, 38(4): 1141−1147. ZHAN Yazhou, MIN Fanlu, SUN Tao, et al. Analysis of causes for ground subsidence induced by slurry shield shutdown in hard plastic caly[J]. Rock and Soil Mechanics, 2017, 38(4): 1141−1147.

(编辑 蒋学东)

Surface deformation characteristics cross the river during slurry shield tunneling

LI Jun1, HUANG Shuai2, HUANG Linchong2, LIANG Yu2

(1. Guangdong Hydropower Planning & Design Institute, Guangzhou 510635, China;2. School of Engineering, Sun Yat-Sen University, Guangzhou 510275, China)

Based on a real project of cross river shield tunnel, the influence of shield driving on ground deformation had been studied, by combing the analysis of field monitoring and three-dimensional finite element simulation. The results show that: the longitudinal settlement is greatly affected by the slurry pressure fluctuation during shield driving. The lateral deformation of ground surface caused by shield driving is different from the one obtained from traditional Peck settlement curve. Longitudinal deformation of ground shows the trend of settlement first and then uplift, and the slurry pressure should be adjusted to control the ground deformation in the process of tunneling. The simulation result is in accord with the field monitoring data, which indicates that the settlement could be under control if some related measurements are adopted.

slurry pressure; ground deformation; shield tunnel; finite element simulation; monitoring analysis

10.19713/j.cnki.43−1423/u.2019.05.019

U455.43

A

1672 − 7029(2019)05 − 1252 − 08

2018−06−21

国家自然科学基金资助项目(51678578 & 51708564)；中国博士后科学基金面上资助项目(2018M633223)；广东省交通运输厅科技资助项目(2016−02−026)；广州市科技计划资助项目(201704020139 & 201804010107)；高校基本科研业务费中山大学青年教培育资助项目(18lgpy31)

梁禹(1986−)，男，湖南长沙人，副研究员，博士，从事隧道工程研究；E−mail：liangyu25@mail.sysu.edu.cn