基于动态加权方法的火电厂综合状态评估

陈 鑫，王鹏雅，王 苗

（三峡大学 电气与新能源学院，湖北 宜昌 443000）

0 引 言

发电厂发电设备的可靠性是电能生产的重要保证。对发电设备实施健康监测和故障诊断，不仅能提高设备的生产稳定性和安全性，还能提升电厂效益，使维修模式由计划检修向状态检修和精细化检修转变。因此，形成一套科学量化的火电厂设备动态加权综合评价方法具有重要的现实意义[1]。目前，对火电厂运行的评价研究主要集中在单因素评价领域，如节能、经济、安全等，而多因素综合评价的研究相对较少[2]。本文通过对火电厂设备各运行参数的分析，构建动态加权综合评价模型。

1 动态加权综合评价模型的建立

对指标数据进行一致化和标准化处理，选定合适的动态加权函数，得到系统运行的实时综合评价分数，构建单个设备完整的评价体系。对上述评价体系进行自主学习，通过使用BP神经网络算法进行多次拟合训练，得到拟合情况较好的神经网络。将系统的运行状态和综合评价分数段对应，进行设备的在线状态评估与诊断。思路流程如图1所示。

1.1 评价指标的一致化和标准化处理

先将偏小型指标做处理，使其转化为偏大型，再对偏大型与中间型数据做如下处理。

中间型：

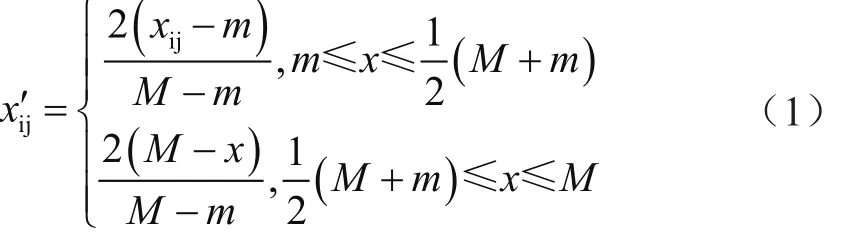
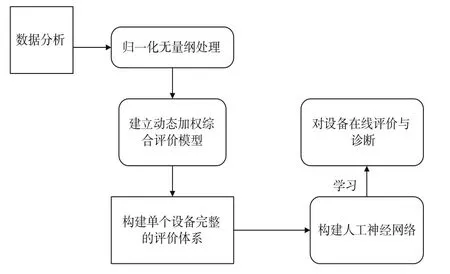
图1 思路流程图

偏大型：

1.2 动态加权函数的设定

从实际问题出发，根据具体问题分析确定相应的权函数。关于不同的指标，权函数的选取既可相同也可不同，本文选取如下几种函数。

（1）偏大型柯西分布函数

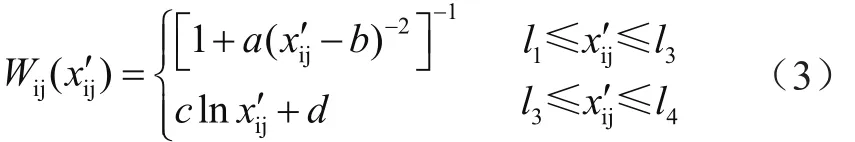
其中a、b、c、d为待定常数，li为第i等级相应的量化数值。

（2）正态分布函数

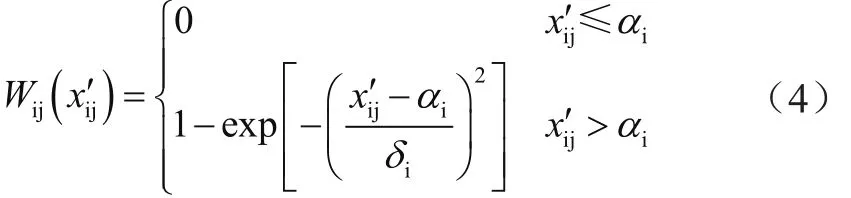
其中αi为两相邻等级的均值，δi取为0.9。

类似地，根据实际情况，变权函数还可取S型分布函数、分段阶梯型分布函数等。

1.3 综合评价模型的构建

根据标准化后的各评价指标值x'ij以及相应的动态权函数Wij(x'ij)建立综合评价模型，对被评价对象做出综合评价[3]。此处，将综合评价模型取为各评价指标的动态加权和，即：

代入收集到的实际实时监测数据，经计算便可得综合评价指标值。

2 火电厂健康监测实例分析

2.1 指标的选取

火力发电厂设备的主要有汽泵前置泵、汽轮机本体以及一次风机[4]等。本文以气泵前置帮泵为例，收集重要的7个运行参数的部分历史数据，如表1所示。

表1 原始数据（部分）

设收集到的3 490组数据为3 490个评价对象，上述的7个运行参数为7个评价指标，则第i组数据的第j个参数值记为xij。对于每一个评价指标，可分为K个等级，对应于每个指标的每个等级都包含一个区间范围记为即当评价指标时，xij属于第K等级。

2.2 数据的预处理

分析上述得到的健康样本库指标值发现，各指标偏向于中间型。将各指标进行一致化处理，有：

再对一致化处理后的数据进行标准化处理，有：

其中：

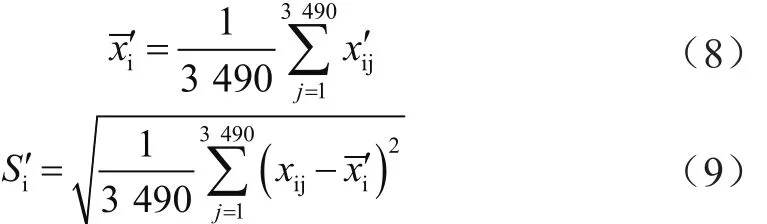
2.3 单个设备的综合状态值

根据实际问题，本文选取动态加权函数为式（2），并计算动态加权和对3 490组被评价对象做出综合评价，即：

根据3 490组实测历史数据，经计算可得汽泵前置泵的综合评价指标值，即一个7×3 490阶的综合评价矩阵(xij)7×3490。图2即为汽泵前置泵评价指标分数的分布直方图。

由图2可看出：汽泵前置泵的历史数据中，随着综合评价分数的增加，呈现的历史次数先是缓慢增加，中间有一个快速增长过程，随后平缓增加趋于最大，到达峰值后呈下降趋势，其频数分布直方图近似呈正态分布曲线（左侧）形状。因此，可以运用统计学知识对综合评价分数划分区间，判断设备的运行状态。

直接进行运算，即可获得系统当前运行的情况分数。统计汽泵前置泵、汽轮机本体、一次风机的综合评价值，结果如表2所示。

图2 综合评价分数直方图

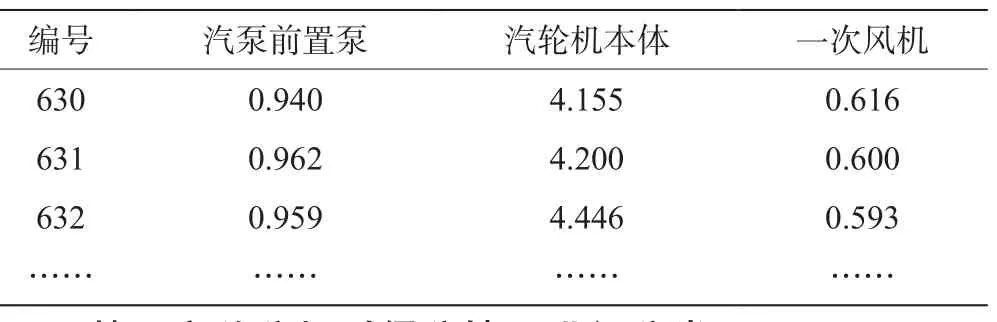
表2 部分综合评价指标值

2.4 基于方差分析对得分情况进行分类

将火电厂设备的运行状态分为4种状态，分别为正常、警告、异常、严重。由上述模型，可以得到各个设备运行的实时综合评价分数，然后利用综合评价分数进行区间划分。综合考虑系统的运行状态和综合评价分数段，对设备进行在线状态评估与诊断。

由统计学知识可知，数据距离平均数越远，分布越稀疏，即：综合评价分数与密度最大区间的偏差绝对值处于[0,2δ]，则认为设备处于正常状态；综合评价分数与密度最大区间的偏差绝对值处于[2δ,3δ]，则认为设备处于警告状态；综合评价分数与密度最大区间的偏差绝对值处于[3δ,5δ]，则认为设备处于异常状态；综合评价分数与密度最大区间的偏差绝对值处于[5δ,∞]，则认为设备处于严重损坏状态。各个区间结果如表3所示。

表3 设备的4种状态的区间值

由表3可知，利用统计学知识，结合实时监测的综合评分与密度最大区间，确定了系统正常状态、发出警告、系统出现异常、系统出现严重损坏下的区间值。将该模型应用于设备的实时监测，可根据综合评价分数判断设备状态，实现对单个设备的在线状态评估与诊断。

3 基于人工神经网络自主学习模型

鉴于火电厂实时运行数据数量庞大，动态加权函数的选取存在一定的主观性，且在计算过程中可能存在误差。因此，本文引入了BP神经网络模型对上述动态加权综合评价模型进行检验与修正。BP神经网络有较强的非映射能力，适于求解内部机制复杂的系统，且有一定的容错能力[5]。图3是神经网络的拓扑结构，采用三层前馈网络，输入层为指标数据，输出一个评价值。

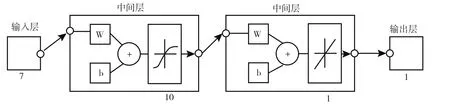
图3 神经网络结构拓补图

将收集的大部分数据作为训练样本，另随机选取20%的数据作为测试集。训练集用来初始化BP网络，确定模型参数，并直至误差满足要求完成训练。图4为训练结果图。

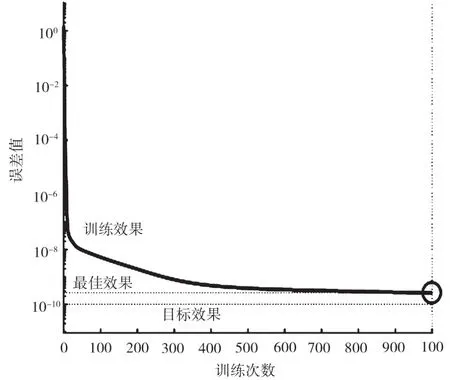
图4 神经网络的拟合

图4 为MATLAB中BP网络的学习与训练过程。可以看出，该算法通过575次训练达到了预设的误差10-10，即训练效果较好，精度较高。

将收集的数据挑出100组作为神经网络的输入样本，图5中十字为原始训练的输出结果，曲线为输入样本作为训练样本得到的结果。十字基本分布在曲线上，说明训练得到的曲线非常接近原曲线，拟合效果较好，即该模型可以进行较好的自主学习，同时验证了动态加权综合评价模型对火电厂设备评估的有效性。

4 结 论

（1）建立动态加权综合评价模型对火电厂实时运行状态做出评估，确定设备分别处于正常、预警、异常、严重4种状态时的综合评价值区间范围。

（2）引入BP神经网络对上述模型进行学习训练，从而实现单个设备在线状态评估与诊断。

（3）在该模型的基础上，可结合层次分析法建立多台设备构成的火电厂机组以及拥有多机组的整个火电厂的实时监控模型，实现各层级的在线状态评估与诊断。

图5 训练前后网络的输出结果