单相交流高频链矩阵逆变器控制策略的研究
2019-06-05徐祖平南京邮电大学通达学院电气工程学院江苏扬州225127
徐祖平,郭 伟(南京邮电大学通达学院 电气工程学院,江苏 扬州 225127)
0 引 言
高频链逆变器中间环节采用高频变压器实现电磁隔离,省掉了体积庞大的工频变压器,还能实现能量的双向流动[1]。因此,随着微网、分布式电源的快速发展,它的应用越来越广泛。高频链电路按照拓扑结构可分为DC-DC变换型和矩阵变换型。其中,矩阵变换型逆变器省去了中间直流储能环节,同时具有单级功率变换、能量双向流动、可靠性及稳定性较高等优点,是当前研究的热点[2]。但是,由于它的后级周期换相结构使用双向开关,因此必须要处理好感性负载的换流问题[3]。
本文以图1所示的矩阵式交流高频链拓扑结构作为研究对象。它主要由直流电源、高频逆变器、高频变压器、矩阵式变换器和输出滤波器等部分组成[4]。本文将重点分析它在不同控制策略下的工作特性和相应的开关动作规律。
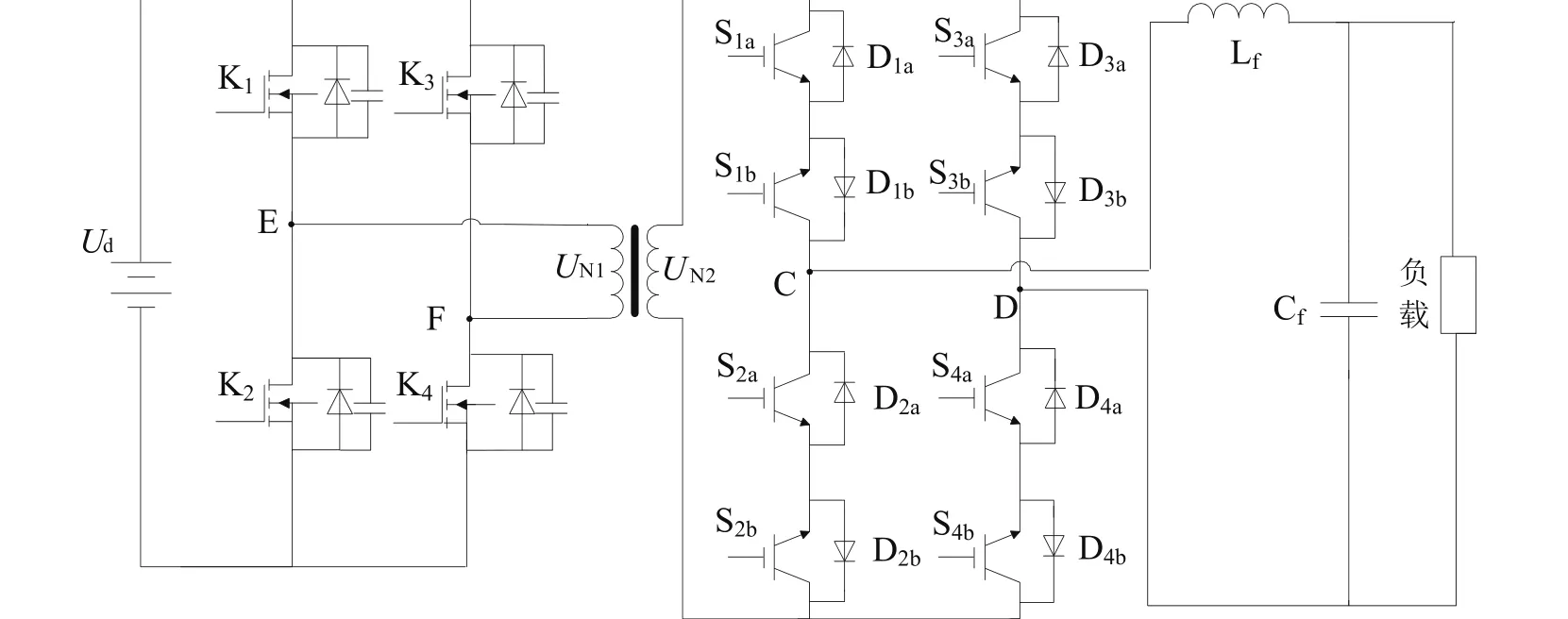
图1 交流高频链拓扑结构
1 控制策略
1.1 单极性移相SPWPM调制
单极性移相SPWPM调制是指前级逆变桥采用移相控制产生SPWPM波,后经矩阵式变换器解调生成单极性SPWM波形。它的控制策略如图2所示,图2(a)给出了各开关管驱动信号和主要环节输出电压波形,图2(b)给出驱动信号的逻辑关系。

图2 单极性移相SPWPM调制控制策略
矩阵式变换器S1a、S1b、S4a、S4b共用一组驱动信号,S2a、S2b、S3a、S3b共用一组驱动信号。它们互补且占空比均为50%。锯齿载波与正弦调制波及其反向信号交截,产生前级逆变桥的驱动信号,其上下桥臂驱动信号互补,且K1和K4驱动信号之间存在移相角θ。变压器原边产生的是双极性三态SPWPM波,不包含直流和低频成分,但含有单极性SPWM波的全部信息,因此可以采用高频变压器进行传输[5]。变压器副边电压经过矩阵式变换器恢复成单极性SPWM波,调制波为正时输出正脉冲,调制波为负时输出负脉冲,最后通过LC滤波器生成稳定的正弦波[6]。
输出电压的幅值不仅与直流电压、变压器变比有关,还与正弦调制波与锯齿载波幅值之比有关。因此,可以通过改变它的幅值比和调制波频率改变输出电压的幅值和频率[7]。
1.2 解结耦调制
解结耦调制策略解耦的原理:在一个高频周期内,高频逆变桥产生的是占空比为0.5的双极性方波信号,如果只考虑半个高频周期,矩阵式变换器的输入可以看做是恒定的直流信号。当变压器初级侧输出电压UN1为正时,S1a、S2a、S3a、S4a组成的逆变桥工作;当变压器初级侧输出电压UN1为负时,S1b、S2b、S3b、S4b组成的逆变桥工作,解耦原理如图3所示。这样矩阵式变换器就被解耦为2个串联独立的普通逆变器,且当一组逆变桥工作时,另一组逆变桥的所有开关管保持关断状态。
解结耦调制策略结耦的原理:将锯齿载波与正弦调制波进行交截,产生两路互补的SPWM信号,在此基础上与高频逆变器产生的方波信号进行逻辑组合,产生矩阵式变换器各开关管的驱动信号,逻辑关系如图4(a)所示。矩阵式变换器各开关管的驱动信号逻辑关系为:

其中,SPWM1和SPWM2是正弦调制波与三角载波比较后产生的两路互补的SPWM信号;V1和V2是高频逆变器产生的占空比为0.5的互补的方波信号,与逆变器的驱动信号同步;各开关管驱动信号波形如图4(b)所示。

图3 解结耦调制方式解耦过程

图4 解结耦调制控制策略
2 仿真分析
在Matlab/Simulink中搭建上述仿真模型,系统参数如下:锯齿载波频率40 kHz,开关频率20 kHz,直流输入电压150 V,变压器变比1:1,滤波电感5 mH,滤波电容3 μF。
2.1 单极性移相SPWPM调制
变压器原边电压分析如图5所示,前级逆变桥输出电压为双极性三态SPWPM波,不含有基波成分,只含有开关频率20 kHz及其奇次倍频谐波成分。因此,可以通过高频变压器进行功率传输,有利于逆变的轻型化和高效性。矩阵式变换器输出电压分析如图6所示,输出电压为单极性SPWM波,谐波成分主要集中在开关频率倍频附近,即40 kHz、80 kHz及以上频率附近。

图5 前级逆变桥输出电压局部波形
矩阵式变换器输出电压波形经滤波器后得到稳定的正弦波,如图7所示,谐波含量少,总谐波失真度为0.29%,电压质量高。
2.2 解结耦调制
变压器原边电压波形分析如图8所示,前级逆变桥产生的是占空比为50%的高频方波,谐波集中在开关频率及其奇次倍频附近。矩阵式变换器输出电压分析如图9所示,与单极性移相调制不同,采用解结耦调制方法矩阵式变换器输出电压为双极性SPWM波,其谐波成分主要集中在开关频率倍频附近。
输出电压经滤波后产生正弦信号,如图10(a)所示,频谱分析如图10(b)所示。此时,正弦电压波峰、波谷处有略微失真,总谐波失真度为0.77%。
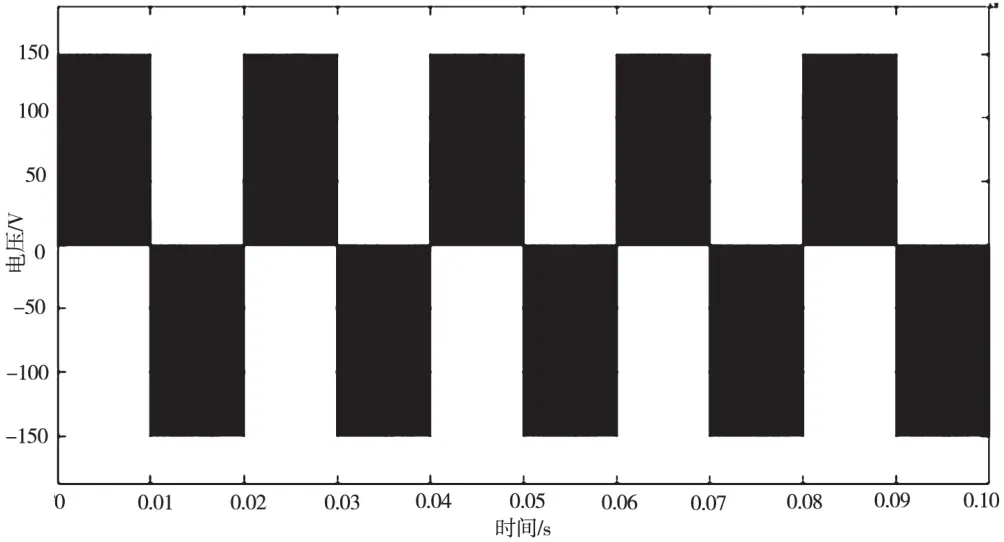
图6 矩阵式变换器输出电压波形

图7 滤波器后输出电压波形及其频谱分析
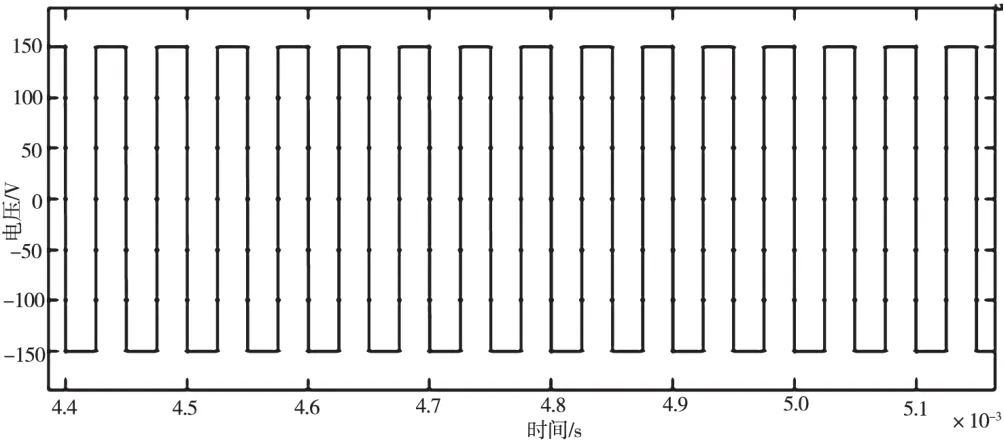
图8 前级逆变桥输出电压局部波形

图9 矩阵式变换器输出电压局部波形
3 结 论
通过仿真实验可知,两种控制策略均能得到理想的输出正弦波。其中,单极性移相SPWPM调制能实现矩阵式变换器零电压开关,解结耦调制则无法实现,但是解结耦调制方式逻辑简单、易实现。此外,解结耦调制方式将矩阵式变换器解耦成两个单独的逆变器独立控制,控制灵活,自由度较好,易于扩展。
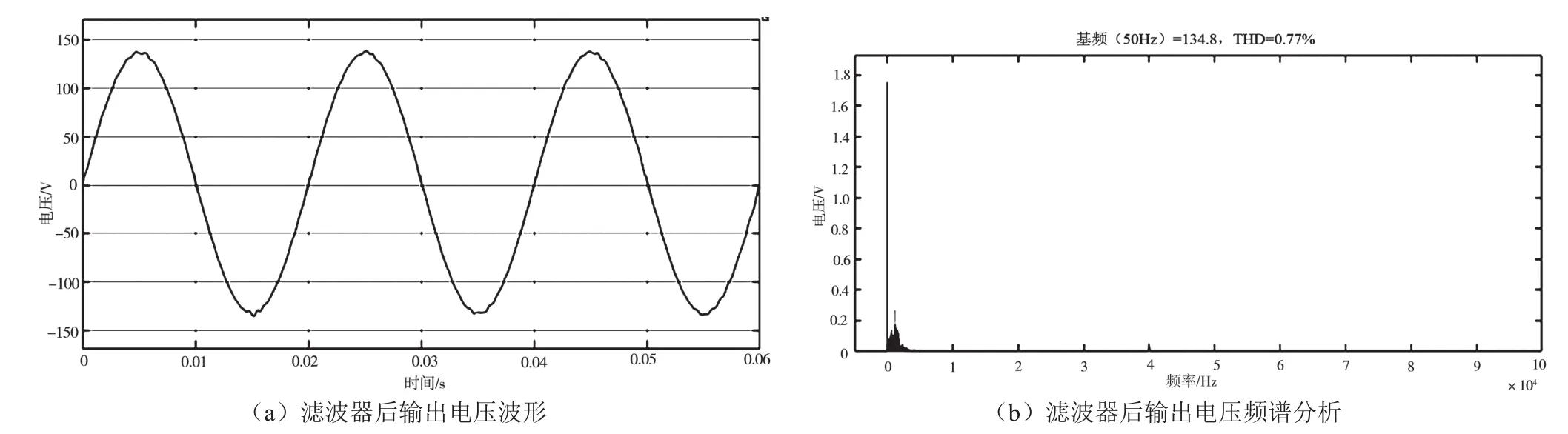
图10 滤波器后输出电压波形及其频谱分析
