全国名校排列组合检测题答案与提示

一、选择题

1.D 提示：在物理、政治、历史中选1科,在其余3科中选2科,则选法有C·C=9(种);在物理、政治、历史中选2科,在其余3科中选1科,则选法有C·C=9(种);物理、政治、历史三科都选的选法有1种。所以学生甲的选考方法共有9+9+1=19(种)。

2.C 提示：分两种情况：第一种,甲、乙只有1人入选,有CC=42(种)方法;第二种,甲、乙都入选,有CC=7(种)方法。所以共有42+7=49(种)方法。

3.B 提示：先不考虑小品类节目是否相邻,保证歌舞类节目不相邻的排法共有A·A=144(种),再剔除小品类节目相邻的情况,有A·A·A=24(种),于是符合题意的排法共有144-24=120(种)。

4.B 提示：第一步：从5本书中任意取出2本捆绑成一本书,有C种方法;第二步：再把4本书分给4个学生,有A种方法。

故共有3×2×2=12(种)分法,选A。

6.D 提示：先把5个空位看成一个整体,然后把4个人排好,有A=24(种)方法,再把5个空位当成整体与另1个空位插入4个人形成的5个空当中,有A=20(种)方法。由分步计数原理可知,共有24×20=480(种)方法。

7.B 提示：本题采用“插空法”,将亮的9盏灯排成一排,两端的灯不熄灭,只有8个符合条件的空位,在8个空位中取出3个空位,插入熄灭的3盏灯有C=56(种)情况。

9.B 提示：由题意知结果有三种情况。(1)甲、乙、丙3名同学全参加,有CA=96(种)情况,其中甲、乙相邻的有CAA=48(种)情况,所以甲、乙、丙3名同学全参加时,甲和乙的朗诵顺序不能相邻顺序有96-48=48(种)情况;(2)甲、乙、丙3名同学恰有1人参加,不同的朗诵顺序有CCA=288种情况;(3)甲、乙、丙3名同学恰有2人参加时,不同的朗诵顺序有CCA=432种情况。

则选派的4名学生不同的朗诵顺序有288+432+48=768(种)情况。

10.D 提示：若3名同学从3个不同的检票通道口进站,则有A=6(种)方法;若3名同学从2个不同的检票通道口进站,则有CCAA=36(种)方法;若3名同学从1个不同的检票通道口进站,则有CA=18(种)方法。综上,这3个同学的不同进站方式有60种。

12.B 提示：当x=1时,1=a0+a1+a2+a3+a4+a5;当x=-1时,35=a0-a1+a2-a3+a4-a5。故a0+a2+a4=122,a1+a3+a5=-121。因为a5=C5520（-1）5=

二、填空题

14.768 提示：当1在首位时,6只有1种排法,7有4种排法,余下4个数共有A种排法,这时七位数有1×4×A=96(个);当1在个位时,同样有96个七位数;当1既不在首位也不在个位时,先把1和6排好,再把7排好,最后再排其余4个数,这时七位数有4×A×3×A=576(个)。因此,共96+96+576=768(个)七位数满足题意。

15.1080 提示：由题设6人应分成2,2,1,1四组,不同的分法种数为45。支愿者分赴第五届亚欧博览会展区服务,不同分配方案有45A=1080(个)。

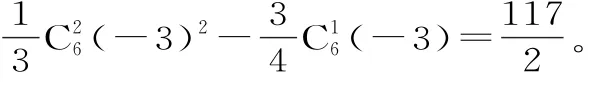
三、解答题

故3名男生必须站在一起的排法有

18.先分类,分5种颜色都用上、5种颜色只用4种、5种颜色只用3种这三种情况,再分别求结果,相加,即可得最终结果。

综上可得,不同涂色方案共有720+1080+120=1920(种)。

19.(1)从9个点中任取2个点,除去共线的情况即可,条数为C-C+1=31。

(2)从9个点中任取3个点,除去共线的情况即可,三角形个数为C-C=80。

20.(1)将小球分成3份,可以是1,1,3或1,2,2,再放在3个不同的盒子中,即先分堆,后分配,有方法。

(2)有35种方法。

(3)只要将5个不同小球分成3份,分法为：1,1,3;1,2,2。共有25(种)方法。

(6)把5个小球及插入的2个隔板都设为小球(7个球),7个球中任选2个变为隔板(可以相邻),那么2块隔板分成3份的小球数对应于相应的3个不同盒子。

故有C27=21(种)方法。

21.(1)(2x-1)2019=a0+a1x+a2x2+ …+a2019x2019。

令x=0,则a0=-1。

由于(2x-1)2019的展开式中含x1的项为,解得a1=4038。

(3)已知等式两边对x求导：4038(2x-1)2018=a1+2a2x+3a3x2+…+2019a2019x2018。

令x=1,得到4038=a1+2a2+3a3+…+2019a2019。所以答案为4038。

22.(1)第r+1项的系数为Crn2r,第r项的系数为Crn-12r-1,第r+2项的系数为Crn+12r+1,依题意得：

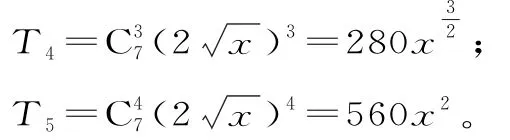
(2)假设第r+1项的系数最大,则：

又因为r∈N*,所以r=5。

展开式中系数最大的项为第6项：

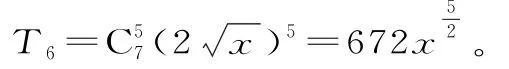
23.(1)先在编号为2,3的盒内分别放入1个,2个球,还剩17个小球,3个盒内每个至少再放入1个球,将17个球排成一排,有16个空隙,插入2块挡板分为3堆,放入3个盒中即可,共有C=120(种)方法。

(2)问题转化为在编号为x,y,z的小球右边各粘贴一个小球,然后将这3个“组合体”插入到剩下14个小球所形成的15个空当中,有C=455(种)方法。

24.设向x轴正方向跳动了x1次,负方向跳动了x2次;向y轴正方向跳动了y1次,负 方向跳动了y2次。则：解得x1=2,x2=0,y1=6,y2=2;x1=3,x2=1,y1=5,y2=1;x1=4,x2=2,y1=4,y2=0。只要满足这三种情况就可以实现目标。第一种情况有1260(种);第二种情况有=5040(种);第三种情况有(种)。所以总共有：1260+5040+3150=9450(种)运动方法。