修正扩维无迹卡尔曼滤波算法研究

任晓斌，聂桂根，李连艳，陈祖岸，雷浩川

(1. 武汉大学卫星导航定位技术研究中心，湖北 武汉 430079； 2. 武汉大学土木建筑工程学院，湖北 武汉430079； 3. 恩施州城乡规划管理局， 湖北 巴东 444300； 4. 青海大学地质工程系，青海 西宁 810016)

X射线脉冲星是一种高速自转的中子星，毫秒脉冲星由于其自转周期稳定性极佳，常常用于导航中。X射线脉冲星导航作为新兴的导航方式，具有良好的发展前景。在导航定位中，如何选择合适的滤波器，建立恰当的噪声模型将直接提高滤波效果，这对于高精度X射线脉冲星导航精度的提高具有重要意义。

目前，研究人员作了大量的滤波处理工作。文献[1]采用最小二乘(least square,LS)算法和KF算法，在星表误差与时间误差递增的条件下，仿真了X、Y、Z方向的位置误差，误差在186.1～2 571.1 m之间。文献[2]运用EKF算法仿真后，得到在1 μs的TOA估计误差下且不考虑其他误差时的位置误差为40.63 m，速度误差为0.019 m/s；运用无迹卡尔漫滤波(unscented Kalman filter，UKF)在上述条件下的位置误差为28.48 m，速度误差为0.012 4 m/s。文献[3]运用扩维无迹卡尔漫滤波(augmented state unscental Kalman filter，ASUKF)算法进行仿真，位置误差为199.4 m，速度误差为0.16 m/s。文献[4]应用CDKF算法进行仿真，位置误差为145.2 m。

本文主要针对脉冲星导航的基本原理，建立脉冲星导航的状态方程和测量方程；然后基于传统ASUKF，建立修正扩维无迹卡尔漫滤波(MASUKF)；最后将该算法与X射线脉冲星导航相结合，进行航天器的位置和速度仿真。

1 基于UKF、ASUKF的滤波算法

1.1 脉冲星导航的原理

X射线脉冲星导航是利用3颗及3颗以上的脉冲星，测量脉冲星到达航天器的时间与到达太阳系质心的时间之差，并通过航天器沿脉冲星与太阳系位置的几何关系，分别确定航天器沿脉冲星至太阳系视线方向的距离，经过处理后得到航天器在以太阳系质心为原点的坐标系的三维坐标。

脉冲星导航的航天器动力学方程为

2n·rn·b-2b·r]

(1)

式中，tSSB为脉冲到达SSB的时间；tSC为脉冲到达航天器的时间，即TOA(time of arrival)；D0为脉冲星到SSB的相对距离；c代表光速；b为SSB相对于太阳系中心的位置矢量,b代表该矢量的数值大小；n为单位矢量，近似认为是常量；r为航天器在SSB中位置矢量，r代表该矢量的数值大小；tSSB与tSC之差代表航天器在沿脉冲星的视线距离方向的投影。右侧表达式中：第1项为一阶Doppler延迟，第2项由周年视差引起，前两项统称Roamer延迟，第3项为Shapiro延迟。

在脉冲星导航中，主要误差源有行星星历误差、角位置误差、脉冲星距离误差等。而所有的误差项都与TOA有关，因此，一个合适的滤波方法可以更为准确地确定TOA。

1.2 UKF的基本理论

UKF是一种将无损变换(UT)和标准Kalman滤波体系相结合的算法，它通过无损变换使非线性系统方程适用于在线性假设下的标准Kalman滤波体系。UKF算法的核心是UT变换，UT变换可以通过构建Sigma采样点获得样本的方差与均值，进而较准确地估计整体的方差和均值，从而可以大幅降低位置误差、速度误差。UKF滤波可以消除部分Roamer延迟、Shapiro效应、Einstein效应所带来的位置误差与速度误差。

1.2.1 UKF算法

UKF算法是以UT变换为基础，采用卡尔曼滤波器的框架，并运用对称性采样法进行滤波的算法。其核心思想为：获取采样点(即Sigma点)并计算其均值、方差和权，然后根据采样值模拟计算整体的均值与方差。UKF算法的步骤如下：

(1) 构建状态方程和测量方程，分别如下

xk+1=f(xk)+wk

(2)

yk=h(xk)+vk

(3)

在确定状态方程和测量方程的误差项wk、vk时，需要假定系统状态的噪声满足高斯白噪声。

(2) 初始化，即

(4)

(3) 计算2n+1个Sigma点及其权值，即

(5)

(4) 计算Sigma点通过非线性函数的传播结果，即

Yi=f(Xi)i=0,1,…,2n

(6)

(7)

1.2.2 基于UKF的X射线脉冲星导航算法

基于UKF的脉冲星导航，即将式(2)和式(3)的状态方程和观测方程转为脉冲星的状态与观测方程，脉冲星的测量方程如式(1)所示，状态方程为

f(x(t),t)=

(8)

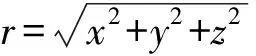
基于UKF的X射线脉冲星导航算法修正了部分因TOA引起的系统误差，在下面的仿真试验中，也可得到位置误差与速度误差的估计。但UKF算法假设状态方程与量测方程均为高斯白噪声，且并未考虑噪声的其他特性，也未针对噪声本身单独进行建模分析，因此针对误差项加以修正是降低误差的下一步任务。

1.3 扩维无味卡尔曼滤波(ASUKF)

1.3.1ASUKF原理

ASUKF在传统的脉冲星信号获取中，在视线方向ni时不能准确获得视线方向，因此脉冲星的方向误差、角位置误差等会大量积累。ASUKF在UKF的基础上，将变量的个数继续扩大，可基于多个测量值在不同维度下进行，可以大大减少由于方向误差带来的偏差，从而使其更加贴近实际情况。

1.3.2ASUKF算法

ASUKF算法是在UT变换的基础上，通过修改误差项获取更接近真值的采样点，然后运用对称性采样的方法进行滤波的算法。其根本思路也是通过采样值模拟计算整体的均值与方差；而最大的不同点在于加入误差项后状态方程与测量方程发生了变化，从而导致采样点发生改变。

(1) 状态方程：在原UKF的基础上增加了3个误差项B1、B2、B3，即

在微课内容上，要保证知识的系统性并做到有始有终。在课程末尾进行一个简明扼要的总结，使知识结构更加立体。同时帮助学生进行知识点的回顾总结，加深所学知识印象。教学者在课程内容安排上还要做到由浅入深、循序渐进，使学习者能够接受课程安排。针对重点内容，可以合理创设问题情景并确定启发性论题，建立为理解而教的目标，使学生对内容产生浓厚的兴趣，主动做课堂的参与者。

X(t)=[xyzvxvyvzB1B2B3]

(9)

(10)

(2) 观测方程考虑系统偏差后方程变为

z(t)=h(X(t))+Bi

(11)

(3) 误差项：该误差项主要修正方向误差和由于Roamer延迟引起的误差

(12)

1.4 修正扩维无味卡尔曼滤波(MASUKF)

1.4.1MASUKF原理

MASUKF在ASUKF的基础上修改了误差项，考虑到Roamer延迟的高阶项，同时在ASUKF的基础上提高了算法的运行效率，缩短了算法的运行时间。

1.4.2 MASUKF算法

MASUKF算法的基本思路与ASUKF算法一致，也将系统偏差看作系统状态的3个变量。因此状态方程(系统轨道动力学方程)和观测方程中均含有系统偏差。在实际中通常需要将方向误差展开至由于赤经赤纬测量误差所带来的角位置误差

(13)

(14)

2 仿真试验

UKF与ASUKF算法在滤波中精度最高，利用两种方法分别进行位置误差的模拟与航天器位置的仿真。在澳大利亚国家天文台官网下载并获取脉冲星的数据。

部分数据如下：航天器位于绕地的MEO卫星，质量为1403 kg，天线相位中心偏差分别为0.641、-0.005、1.177 m。起始航天器在J2000.0坐标系下的位置X、Y、Z分别为-16 242 041.827、-5 242 312.694、22 071 892.826 m，速度分别为-2669、-3 676.998、-887.52 m/s。长半轴a=27 908 632.497 m，e=0.000 5，轨道的倾角i=55.521°，升交点赤经Ω=80.526°，近地点角距ω=165.303°，平近点角M=301.079°。

2.1 ASUKF与UKF算法比较

仿真时间为2008年2月13:00—2008年2月14:00，间隔为1 min。根据上文中设计的UKF与ASUKF滤波器分别仿真航天器的坐标值。其中，在t时刻航天器在地心惯性坐标系J2000.0内的坐标值可由精密星历拟合得到，通过仿真试验，即可得到UKF与ASUKF的位置误差与速度误差。

2.2 仿真结果分析

选取上述脉冲星进行航天器导航，分别将状态方程与测量方程进行速度误差与位置误差的估计，模拟在150 s的步长下UKF与ASUKF算法的误差。结果如图1所示。灰色表示UKF，黑色表示ASUKF。结果显示，UKF算法在x方向的定位精度约为172 m,ASUKF算法在x方向的定位精度约为102 m。ASUKF较UKF算法估计的位置误差与速度误差均较小，虽然位置误差与速度误差存在突变点与极值点，但二者均可收敛，在一定精度要求下可满足条件。

原来位置为：-16 242 041.827、-5 242 312.694、22 071 892.826 m，经脉冲星动力学方程导航后确定的航天器位置为-16 241 258.631、-5 242 826.321、22 072 760.739 m，两种导航方法的位置误差及速度误差分别见表1、表2。

表1 两种导航方法的位置误差 m

表2 两种导航方法的速度误差 (m/s)

将航天器的真实状态(-16 242 041.827，-5 242 312.694，22 071 892.826)加入UKF与ASUKF算法中，可以直观进行滤波前后航天器位置的对比。模拟在航天器x方向速度1 km/s，y方向速度1 km/s，z方向1 km/s的情况下的滤波轨迹。结果如图2—图5所示。

在航天器运动状态确定的情况下，ASUKF均能较好地模拟航天器的运动状态，其精度远远大于UKF算法。在构建误差项时考虑角位置误差，因而运用ASUKF算法进行估计航天器真实位置的精度较高。

2.3 ASUKF与MASUKF算法比较

在加入误差项Bi后，对航天器进行仿真分析，模拟航天器在3方向初始运动为匀速运动的状态。为提高仿真精度，仿真步长为10 000 s。选x方向分析其位置误差(y、z方向类似)，加入误差项后的模拟结果如图6、图7所示。

由图6、图7可知，在仿真步长10 000 s时，MASUKF算法的位置误差均值与方差小于ASUKF算法。在匀速运动下，MASUKF的位置误差均值约为99.43 m，略小于ASUKF算法的100.21 m；MASUKF的速度误差均值约0.001 25 m/s，略小于ASUKF算法的0.001 29 m/s。而ASUKF算法的均方差也小于MASUKF算法，因此MASUKF算法在模拟过程中的性能更佳。

2.4 3种算法的运行时间对比

在Matlab中对3种算法分别设置起止时间，查看3种算法的运行时间，如图8所示。

由于UKF算法没有考虑误差项，精度相对较低、计算量较小，因此其运行时间最短。而MASUKF相较ASUKF算法而言显著地提高了0.975 s，大大节省了程序的运行时间。

3 结 语

本文主要研究了具有脉冲星方向误差的ASUKF导航滤波算法的仿真实现，并自行设计了MASUKF算法进行试验。首先分析了脉冲星方向误差产生的原因及其对导航性能的影响，比较了UKF、ASUKF和MASUKF算法的原理，并在近地轨道上对该方法进行了仿真验证。仿真结果表明，ASUKF算法较UKF算法而言精度较高。而与ASUKF滤波算法相比，MASUKF算法的导航定位、测速精度明显更高,运行时间更短，是一种更好的算法。