基于三维混沌序列的DEM置乱与还原方法

仲浩宇，王中元，李安波,2,3

(1. 南京师范大学地理科学学院，江苏 南京 210023; 2. 南京师范大学虚拟地理环境教育部重点实验室，江苏 南京 210023; 3. 江苏省地理信息资源开发与利用协同创新中心，江苏 南京 210023)

地理信息事关国家安全和社会利益，其安全防护是当前地理信息行业亟待解决的难题[1]。随着计算机网络、云数据等技术的迅猛发展，网络数据传输的安全问题更是日益严峻。DEM数据作为国家空间数据基础设施的重要内容，一旦发生泄密事件，会带来巨大的社会安全隐患和经济损失。因此，如何保障DEM数据在网络传输时的安全性，是当前需要解决的重要问题之一。

DEM数据的保护方式主要有数据加密[2]、数字水印[3]技术。其中，数据加密基于DEM数据的特征分为DEM数据伪装[4]和DEM数据置乱。这两种技术利用DEM所具有的空间和数值特征，实现DEM数据加密；数字水印技术虽然在DEM数据的版权保护和数据泄露溯源等方面应用广泛，但是DEM数据被窃取后仍可以继续使用，没有从根本上解决数据安全问题。

文献[5]使用空间域生成的三维曲面与原始DEM数据进行叠加，提出了一种基于模糊关系和带参数曲面的DEM伪装算法，具有一定的可逆性与高效性；文献[6]将伪装算法与数字水印技术相融合，实现了DEM数据伪装。与数据加密、数字水印技术相比，DEM伪装算法虽然具有一定优势，但也存在一定的不足。文献[7]利用置乱原理有效改善了当前DEM伪装算法大量占用内存空间、数据误用等方面的问题，但是数据还原后仍存在一定的误差。

综上，本文拟基于三维混沌序列，在对DEM文件先后进行高程置乱、位置置乱和文件头置乱处理后，使置乱数据失去高程变化的空间连续性与数值连续性，实现置乱DEM数据的无损、盲式还原。

1 研究方法

DEM数据中每个栅格具有X坐标、Y坐标和高程3个基本属性。DEM的总体置乱可以从高程和位置两个方面进行置乱。其中，高程置乱用于破坏DEM高程值的真实性；位置置乱用于破坏高程位置的连续性；其次，针对DEM中的3个基本属性，基于三维混沌映射一致化进行高程置乱和位置置乱，可提高算法处理效率和算法安全性；最后，加密DEM文件头中的基础信息，进一步提高算法安全性(如图1所示)。

1.1 三维混沌序列生成

混沌系统主要有一维Logistic映射[6]、二维Hénon映射[7]、三维Lorenz映射[8]和通过多个方程进行升维的复合混沌系统。本文使用三维混沌映射生成混沌序列，三维混沌序列生成函数的定义为

(1)

式中，x0、y0、z0为混沌系统的初值，且x0∈(0,1),y0∈(0,1),z0∈(0,1)；x1、y1、z1和x2、y2、z2分别是根据初值和式(2)、式(3)计算出的迭代数值；xk、yk、zk和xk+1、yk+1、zk+1分别是迭代k次和k+1次后的数值；k为迭代次数，k>2；mod 1表示仅取数值的小数部分。

(2)

(3)

此三维混沌映射使用了类斐波那契数列的方式构造基础混沌序列，输入参数的精度决定了混沌序列的复杂度。为此，建议使用小数位数为3以上的序列初值。首先输入混沌序列m初始混沌参数{x0,y0,z0,ρ,σ}，其中ρ∈[100,1000]内的整数，定义为混沌序列截取长度，σ∈(0,1)为二值化序列阈值。然后计算初始参数x1,y1,z1,x2,y2,z2}，根据三维混沌方程(式(1))，生成长度为L1=(row+col+LH)的混沌序列X、Y、Z，其中row为行数，col为列数，LH为最大高程值转为二进制的位数(通常取14)。

初始混沌参数{x,y,z,ρ,σ}是还原时重构混沌序列的必要条件。这些参数作为本算法的还原密钥，即使在算法已公开的情况下，如果密钥未知，也无法还原秘密DEM数据，遵循算法的公开安全性原则。

1.2 高程置乱

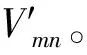
高程置乱的具体处理流程如下：

(1) 将DEM数据存入大小为row×col的矩阵A中，对于浮点数型的高程值仅处理整数部分。

(2) 混沌序列Z的二值化处理。初始混沌序列{X,Y,Z}的数值均分布在[0,1]区间内，通过混沌序列二值化，得到0、1序列。本文对序列Z使用式(4)进行线性离散化，得到二值化序列Z′，即

(4)

(3) 栅格高程值Vmn的二进制处理。将Vmn转化为使用14位二进制值表示的0、1序列B={b0,b1,…,b13}。若m+n为偶数，则二进制序列不变；若m+n为奇数，则序列低7位与高7位进行互换，得到序列B′={b7,…,b13,b0,…,b6}。

(4) 基于栅格位置的二进制子串截取。根据m、n选取序列Z′中的14位构成序列Zsub={z′m+n,z′m+n+1,…,z′m+n+13}。

(5) 异或运算。按照m+n的奇偶性使用序列B或B′按位与序列Zsub异或，若Vmn为正则将第15位补0，否则第15位补1。

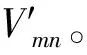
(7) 重复执行步骤(3)—(6)，直至所有栅格的高程值置乱处理完毕，得到矩阵A′。

1.3 位置置乱

对A′进行位置置乱的主要步骤为：

(1) 混沌序列X、Y的截取或补齐。判断混沌序列X、Y的长度L1是否大于ρ，若大于ρ则取出该混沌序列的前ρ位；否则使用式(1)补足ρ位构成序列X′、Y′。

p=mmodρ

(5)

在序列J′x中遍历寻找与p值相等的元素，记录其下标为mID，并根据式(6)生成与该位置进行对换的行号m′。若m′<0则将m′加上行数。

m′=(m-p+mID)mod row

(6)

q=nmodρ

(7)

在序列J′y中遍历寻找与p值相等的元素，记录其下标为nID，并根据式(8)生成与该位置进行对换的行号n′。若n′<0则将n′加上列数。

n′=(n-q+nID)mod col

(8)

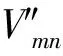
1.4 文件头置乱

DEM的文件头中保存了DEM的元数据(见表1)，基于这些数据，用户可以直接定位到DEM数据所在的真实位置。如果不进行加密处理，势必增加DEM置乱数据被破解的风险。X方向偏移，Y方向偏移和单元格大小，是决定DEM数据真实位置的决定因素，需对这3个数值进行置乱处理，即

表1 DEM文件头描述

(9)

经过上述处理，一方面置乱后的X方向偏移，Y方向偏移数值与原数值完全不同，可将DEM的空间定位转换至另一个未知位置；另一方面，置乱后的单元格大小影响到最终DEM表示范围的大小，将DEM的覆盖范围进行了缩放处理。

1.5 置乱DEM的还原处理

置乱数据还原的关键在于提供正确的密钥，并按照置乱相反的流程执行还原操作，其对应的还原流程为先位置还原后高程还原。

DEM置乱数据A″还原的具体流程为：

(1) 基于还原密钥生成混沌序列。基于用户提供的密钥{x0,y0,z0,ρ,σ}，根据式(1)—式(3)生成初始混沌序列X、Y、Z。

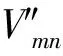
(4) 文件头还原。使用参数{x，y，z，ρ，φ}，根据式(9)再进行一次异或运算，即可得到原始的DEM文件头信息。

所有位置运算完毕后即完成了置乱矩阵的所有复原工作，得到最初的高程矩阵A。本文算法的DEM还原流程中无需原始数据的参与，是一种稳定的盲还原方式，并且还原后的DEM数据与原始DEM数据完全相同，保证了DEM数据的精度不受损失。

2 试验与分析

本文采用ASCII格式的1∶50 000某涉密区域DEM数据(如图4所示)作为试验数据，该数据中高程数据类型为整型，存在数值为-9999的Nodata区域。

本文试验中，首先输入原始DEM与混沌参数，根据混沌参数生成混沌序列；然后使用混沌序列分别对DEM的高程、位置和文件头依次进行置乱；最后，输出置乱DEM。DEM的还原是置乱的逆向操作，通过还原处理，最后得到原始的DEM数据。

为了评价本文算法的优越性，下面主要从混沌序列周期检验、安全性分析、置乱度分析和时间效率分析4个方面对算法进行分析。

2.1 不同置乱参数对混沌序列周期性的影响

通过混沌映射或混沌运动获取的混沌序列密码，由于其混沌运动轨道表现出的内随机性、遍历性和初值敏感性等特性，使得混沌系统在使用仅有微小变化的混沌参数进行有限次的迭代后可以得到完全不同的序列[9]，这样的特性使得混沌序列密码满足了混沌序列在抗破解方面的要求。同时，混沌序列密码在进行大量迭代后随机性会产生大幅度减弱的现象，即混沌密码在序列中出现一定的周期性重复。这一周期性重复降低了算法的安全性，因此混沌序列密码需要尽量减弱周期性，增强随机性，选择混沌映射时尽量选取随机性强的混沌映射。

本文使用的混沌序列仅有0和1两种数字构成，统计学中的游程检测法是简单且高效检测序列中是否存在周期性子序列分布的有效方法[10]，其运算结果为重复样本发生的概率，计算结果越小表示周期性越弱。本试验使用C++编写生成混沌序列的程序，将生成的混沌序列导出至文本文件，使用SPSS软件中的游程检验功能进行序列周期性检验，结果数据使用渐进显著性表示。构建混沌序列总共需要4个参数，其中前3个参数控制混沌序列的生成，最后一个参数控制序列的二值化。试验参数见表2，其中A组为参照组，B组大幅增加了参数Y的值，C组小幅减少了参数Z的值，D组替换了参数σ的值。

表2 序列周期性检测

通过SPSS的分析结果(见表2)可以看出，以上4组数值分布不一致的混沌参数生成的混沌序列的渐进显著性在序列长度为2136的情况下均为0，反映出该三维混沌映射生成的混沌序列具有很强的随机性，不易产生“弱周期性”现象，符合混沌序列随机性强的要求。

NIST发布的STS(statistical test suite)测试包是当前国际上较为权威的对伪随机序列进行性能测试的工具，测试结果通过P-Value体现，同时会给出多个模板的测试通过率。其中包含15项指标测试，混沌伪随机序列的随机性检验中仅需使用频数测试、分块频数测试、游程测试、频谱测试和近似熵测试这5项测试并检验其运算结果即可。

首先在Linux环境下安装STS-2.1.2测试包；其次根据上述组别A密钥， 生成大小为1亿 bit 的伪随机0-1序列并输出为二进制文件；然后运行STS工具包，本次测试中将数据分为2000组，每组数据50 000 bit，按上述5项指标进行测试；最后得到的测试结果见表3，可以看出本文使用的混沌序列通过了全部5项测试，整体上具有较好的随机性。

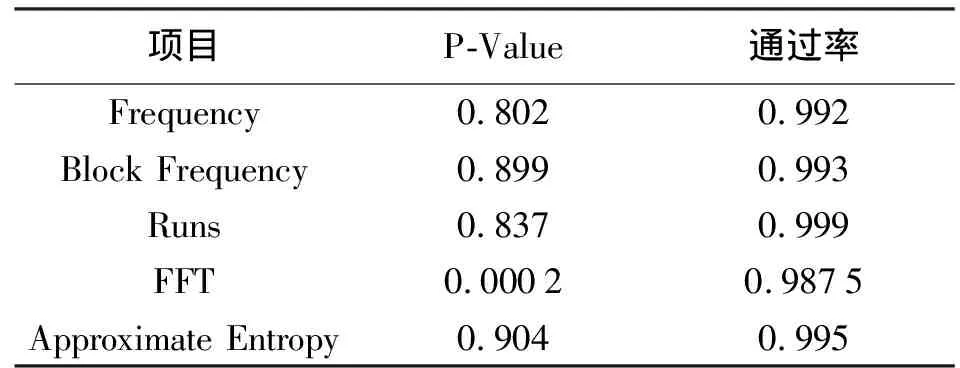
表3 STS测试结果

2.2 安全性分析

传统的加密方法可以使用计算机暴力测试的方法求解密钥，实现加密数据的破解。本文还原算法的核心是使用正确的还原参数生成混沌序列，实现DEM数据的还原。优秀的置乱与还原算法应当具有极高的密钥敏感性，本文试验体现在还原参数只要发生一点变化，便无法还原出原始DEM。

本文提出的基于三维混沌映射的DEM置乱算法，在进行置乱和还原时需要提供5个参数{x0,y0,z0,ρ,σ}，其中{x0,y0,z0,σ}为(0,1)区间内的任意位小数，ρ∈(1,+),ρ∈Z。本文试验使用近似的加密参数和解密参数来验证算法的抗破解性能(见表4)。为遵循单一变量原则，设置A组为参照组，使用相同的参数进行置乱和还原，B、C、D、E组为对比试验组。由于前3个参数共同控制混沌序列的生成，体现的功能性相同，仅在B、C两组进行比对；D组修改了参数ρ的值，该值对位置置乱至关重；E组修改了参数σ的值，该参数仅控制混沌序列二值化时的初始值。5组参数的置乱与还原结果如图5所示。其中图5(a)为置乱后结果，图5(b)—(f)分别为A、B、C、D、E组的还原结果。

表4 参数与还原度

通过图5(a)可以看出，本文算法完全破坏了DEM的空间连续性；从图5(b)可知使用相同的混沌参数可以完全复原置乱后的DEM，证明该算法具有完全的可逆性，还原出的数据没有任何的精度损失；从图5(c)—(f)可知还原参数只要出现略微的不同就无法实现置乱DEM的还原，所有置乱参数均具有数值敏感性，整体安全性强。

2.3 算法置乱度分析

对于置乱后DEM数据的置乱度，本文使用基于差分统计特性的图像置乱度盲评价线性模型进行验证。该模型通过计算置乱后图像的差分图像，统计差分图像灰度分布直方图，通过直方图数值分布斜率特征，求解斜率绝对差因子，数值越大表示置乱度越好[11]。

由于地表高程数据具有潜在的空间连续性，大部分情况下高程变化连续且有规律，因此，DEM影像的差分图像的灰度分布主要集中在中心区域，并且沿两侧呈快速下降的趋势[12]。经置乱后的图像灰度值分布随机，导致差分图像对应的差分值分布均匀，直方图呈现出沿中心线性下降的趋势。为了验证该方法在DEM数据置乱应用中的可行性，本文试验使用DEM进行测试，图6(a)为正常的DEM图像，其差分直方图如图6(b)所示，呈现出从中心快速下降的趋势；图6(c)为使用ArcMap生成的随机栅格图像，其差分直方图如图5(d)所示，沿中心向两侧呈线性缓慢下降趋势。从图6可见该方法适用于DEM影像置乱效果的评定。

使用两组不同的置乱参数对DEM进行置乱，原始图像及置乱图像差分直方图如图7所示，置乱程度见表5。本算法置乱的DEM数据，置乱度均达到0.85以上，具有较强的迷惑性。

表5 置乱参数与置乱度

2.4 算法时间效率分析

为检验在不同数据量下的算法时间消耗，本文试验中使用ArcMap的创建随机栅格功能构建大小不同的随机栅格，大小分别为200×200、400×400、600×600、800×800、1000×1000。编写程序获取算法开始执行和运算结束的系统时间并相减，得到算法执行的总时间。不同数量的栅格在本文算法下进行置乱的时间消耗见表6。进行函数拟合后，发现本文算法的时间消耗与DEM中的栅格数量近似呈线性关系，算法时间复杂度较低(如图8所示)，说明本文算法适用于大数据量DEM的置乱处理。

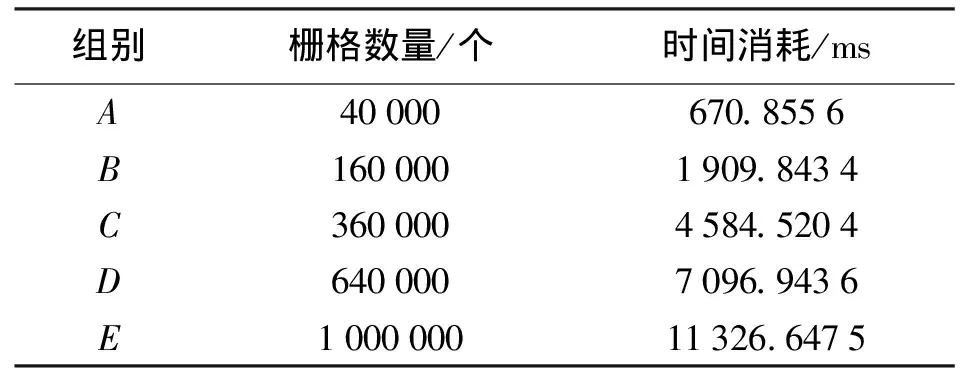
表6 时间复杂度检测

3 讨 论

(1) 本文DEM置乱方法主要使用三维混沌系统构建混沌序列对DEM数据进行置乱操作。同样可以使用一维或二维混沌系统，如Logistic混沌序列，均可达到不错的置乱效果，但混沌序列的周期性较差，置乱强度不足。

(2) 本文算法与DEM的具体格式无关。虽以ASCII格式文件进行试验，但具体方法可应于不同格式的DEM文件。

(3) 由于异或运算的结果均为正值，即高程在海平面以下区域DEM的运算，在进行还原时所有负值会归0，通过在转换时记录二进制数符号位的方式，可以有效避免负数无效的情况。本文应用符号位的概念解决了高程值为负数时异或运算产生的问题。

(4) 本文算法的置乱流程为首先进行高程置乱，然后进行位置置乱，最后进行文件头置乱。在实际的应用中这3个置乱步骤的顺序可以任意调换，最终的运算结果无较大差异，但是在DEM数据还原时需要按照置乱顺序的逆序进行操作。

(5) 本置乱算法虽然保护了DEM数据在网络传输过程中的安全性，但是没有进行DEM版权信息的保护。可以在本置乱算法的基础上融入DEM数字水印算法，在保证数据安全的同时保护数据版权。数字水印可以显式添加在置乱前和置乱后的DEM数据中，也可以隐式添加在高程置乱后、位置置乱前的DEM中间数据中。携带隐式数字水印的置乱算法需要在还原过程中检测并去除图像中的水印数据。

4 结 语

本文主要采用基于三维混沌系统的DEM置乱算法和还原算法，实现了以ASCII格式存储的栅格地理数据的置乱与无损还原处理，并通过差分图像的统计特征验证了该算法的置乱强度。试验表明，本文方法可以有效地保证DEM数据的传输安全，并且具有较好的抗暴力破解能力和自动化特性。试验数据在置乱前和还原后的一致性达到100%，基本满足了以ASCII格式存储的栅格数据在网络安全传输、封装存储等方面应用的需求。