一种2π视场高分辨热等离子体分析仪设计与仿真
2019-06-05孔令高张爱兵
苏 斌,孔令高,张爱兵,3,4
(1.中国科学院国家空间科学中心,北京 100190;2.中国科学院大学,北京 100049;3.天基空间环境探测北京市重点实验室,北京 100190;4.中国科学院空间环境态势感知技术重点实验室,北京 100190)
0 引 言
在空间热等离子体探测中,大视场是仪器设计的基本需求之一,通常需要全空间(4π)视场实现等离子体三维分布的探测。带顶盖半球形静电分析器是一种广泛采用的探测方案[1-2]。这类静电分析器具有360°(方位角)×约8°(俯仰角)的固有环形视场,被广泛应用于自旋稳定卫星上,利用卫星自旋可以实现4π空间测量[3-7]。在三轴稳定卫星上,由于其俯仰角固有视场小,需要采用对称的静电偏转板设计增大俯仰角视场。STEREO卫星的PLASTIC载荷将俯仰角扩大到±20°,Juno探测器的JADE载荷扩大到±35°,MAVEN卫星的SWIA/SWEA/STATIC载荷采用大偏转板将俯仰角扩大到±45°[8-12],Parker太阳探测器的SWEAP载荷将俯仰角视场扩大到±60°[13]。然而在三轴稳定卫星平台上,扩大了俯仰角的单台探测器仍然无法实现4π空间探测,通常需要至少两台探测器配合实现。欧空局的Solar Orbiter卫星的载荷SWA/EAS采用对称偏转板实现±45°俯仰角视场,两台仪器朝向不同方向达到了接近4π的探测视场[14]。
另外一种获得4π探测视场的方法是在三轴稳定卫星平台上,通过偏转板的不对称设计,实现单台仪器具有2π半球形视场,两台仪器安装在相反方向上相互配合即可覆盖4π全空间视场,比如日本SELENE卫星的PACE载荷。PACE的偏转板采用幂函数剖面设计,以俯仰角中心轴线为x轴,上下偏转板剖面曲线分别正比于x2.4和x2.9,将俯仰角由0°扫描至90°,实现了2π半球视场[15-16]。这种设计获得的俯仰角与偏转电压关系曲线的线性度较好,但缺点是俯仰角接近90°时,方位角分辨率明显变差。在0°和90°俯仰角附近仪器的几何因子也有明显的下降,俯仰角范围内的几何因子响应一致性不好。
此外,空间粒子类仪器通常对特定区域的特定对象进行探测,具有固定的几何因子,即具有固定的通量动态响应范围。而在某些跨磁层和太阳风探测任务中,卫星轨道贯穿内磁层、磁鞘和太阳风,等离子体通量变化可达3个量级,尤其当日冕物质抛射(CMEs)发生时,太阳向地球空间抛射大量等离子体,会大大增加地球附近等离子体通量[17-18]。入射等离子体通量超过某一临界值时,仪器计数就会达到饱和。固定几何因子的仪器无法覆盖如此大的通量动态范围[19]。
为解决目前2π视场的等离子体探测器设计的不足,在已有空间等离子体仪器基础上,本文介绍的热等离子体分析仪(Hot plasma analyzer,HPA)采用球形剖面静电偏转板,实现俯仰角0°~90°之间的连续扫描,获得2π半球形视场,同时使用两台仪器可实现4π全空间覆盖。且通过视场偏转系统的结构优化,提高了角度分辨率。此外,利用顶盖电压控制方式实现几何因子连续可变,满足大通量动态范围热等离子体的探测需求。
1 热等离子体分析仪的设计与建模
1.1 仪器指标需求
以三轴稳定卫星平台上开展热等离子体探测为任务需求,根据空间热等离子体能量与通量特点,HPA需要对50 eV~20 keV能量范围的热等离子体进行高分辨率探测,利用两台仪器的联合探测视场将达到4π。单台仪器指标要求见表1。
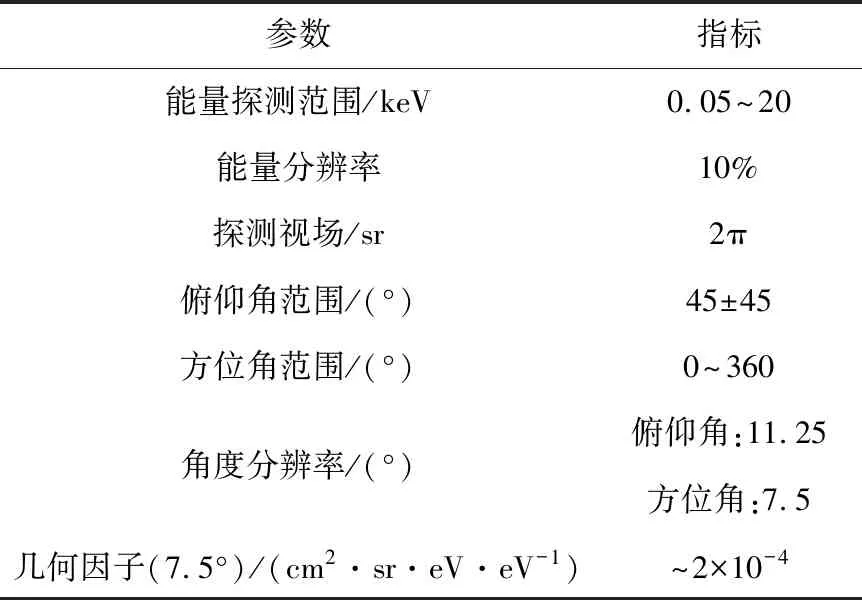
表1 热等离子体分析仪主要指标要求Table 1 Main required specifications of HPA
1.2 理论基础与设计方案
HPA主要包括探头和电子学箱两个部分。探头主要用于对入射等离子体进行能量和方向分析,将信号输出给电子学箱;电子学箱对输出信号进行处理分析。探头具有旋转对称结构。图1给出了探头组成部分的剖面结构,从上到下依次包括:视场偏转系统(FOV deflector system,FDS)、可变几何因子系统(Variable geometric factor system,VGFS)、准直通道、静电分析器(Electrostatic analyzer,ESA)、微通道板(Micro-channel plate,MCP)和阳极。带箭头虚线表示的是沿特定俯仰角入射并成功飞出静电分析器到达微通道板的等离子体轨迹。

图1 热等离子体分析仪探头基本结构剖面Fig.1 Layout of HPA sensor head
等离子体首先进入视场偏转系统。视场偏转系统由两块圆形剖面的静电偏转板组成,两块偏转板对称轴线俯仰角为45°,偏转板加不同大小的扫描电压实现对不同入射俯仰角等离子体的轨迹偏转,入射俯仰角由偏转电压和等离子体能量决定。可变几何因子系统包含一块顶盖电极,顶盖加电压时,顶盖电场改变入射等离子体的轨迹,影响飞出静电分析器的等离子体通量。
静电分析器由两块同心球形极板组成,等离子体进入静电分析器后在极板间径向电场引导下穿过狭缝。球形极板的平均半径R0和狭缝宽度d决定了静电分析器因子k:
(1)
式中:k是静电分析器的固有特性参数,球形极板加电压时,只有特定的能量电荷比值(E/q)的等离子体能通过狭缝。内极板加电压VI,外极板接地时,能通过狭缝的等离子体E/q与电压VI的关系如下[20]:
E/q=k·VI
(2)
式中:E为等离子体能量,q为电荷数。电子学提供给静电分析器的电压VI通常是一个确定的范围,因此静电分析器因子直接影响仪器的可探测能量范围。Young等[21]对能量分辨率与静电分析器因子k的关系进行了研究,并给出了近似关系式:ΔE/E~1/k,即能量分辨率与k成反比,k的大小直接影响能量分辨率。
球形静电分析器会对以固定方位角入射的等离子体产生聚焦作用,在静电分析器出口附近形成聚焦点,如图2所示。聚焦产生的焦点落在微通道板上,记录等离子体位置信息。微通道板将接收到的电荷信号放大,并将电荷脉冲输出给电子学。后端阳极被划分为48等份,每块为7.5°,实现方位角分辨。

图2 球形静电分析器的聚焦作用示意图Fig.2 Ion beam focusing of spherical ESA
1.3 仿真模型的建立
对静电分析类的等离子体探测器,SIMION是最常用的仿真软件[22]。仿真模型的建立主要有两部分内容:①建立探头静电场模型;②建立等离子体入射源模型。
根据HPA探头尺寸建立传感器结构模型,SIMION根据电极电压计算探头内部电场。图3给出了VI=-178 V,上偏转板电压Vupper=-200 V,其他电极接地时的电场等势线图。模型采用笛卡尔坐标系:以旋转中心为Z轴,水平轴为X轴,Y轴符合右手定则。

图3 HPA探头内部电场等势线图Fig.3 Equipotential lines in HPA head sensor
仿真所用等离子体入射源模型的建立采用蒙特卡罗方法。以均匀随机抽样方式产生N个等离子体作为入射源。SIMION根据HPA内部电场和等离子体信息计算粒子的运动轨迹,并根据需要记录指定位置的粒子属性参数(能量、位置、速度等)。
2 HPA仪器性能
2.1 能谱范围与能量分辨率
入射源中所有能通过静电分析器狭缝并到达微通道板的等离子体被定义为有效等离子体。图4给出了VI=-178 V时的有效等离子体能谱分布图,能谱符合高斯分布。峰值能量E=1070 eV,由式(2)计算得静电分析器因子k=6.03,能量分辨率η定义为能谱半高全宽ΔE与E之比,η=ΔE/E=9.75%。k和η均为仪器的固有特征参数,和仪器结构尺寸有关,与等离子体能量和电压无关。
由电压范围和式(2)计算,可探测等离子体能量范围为30.2 eV ~24.1 keV,满足指标需求。
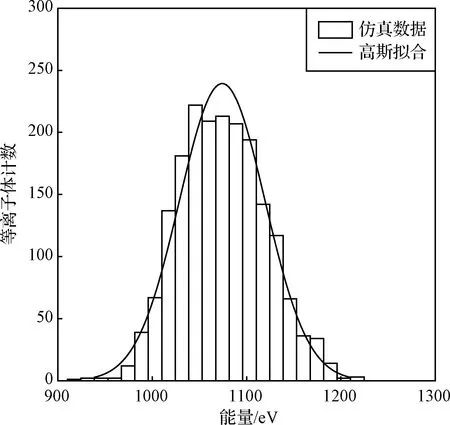
图4 VI=-178 V时能谱图Fig.4 Energy spectrum when VI=-178 V
2.2 俯仰角视场与俯仰角分辨率
由于准直通道限制,HPA固有俯仰角视场很小,仅约几度。图5是偏转板接地时的入射俯仰角分布,入射俯仰角符合高斯分布,峰值为45°,最大跨越4.5°。高斯分布半高宽即为俯仰角分辨率Δα,仿真结果为1.95°。
为了扩大俯仰角视场范围,引入了视场偏转系统。视场偏转系统采用了球形剖面偏转板设计,通过对上下偏转板加扫描高压,对入射等离子体俯仰角进行偏转。不同于PACE偏转板的设计,HPA采用的球形剖面偏转板,既改善了PACE所用幂函数构型存在的几何因子在俯仰角接近0°和90°时下降幅度过大的问题,也提高了方位角分辨率。经偏转电场作用后的俯仰角与偏转电压和等离子体能量相关。
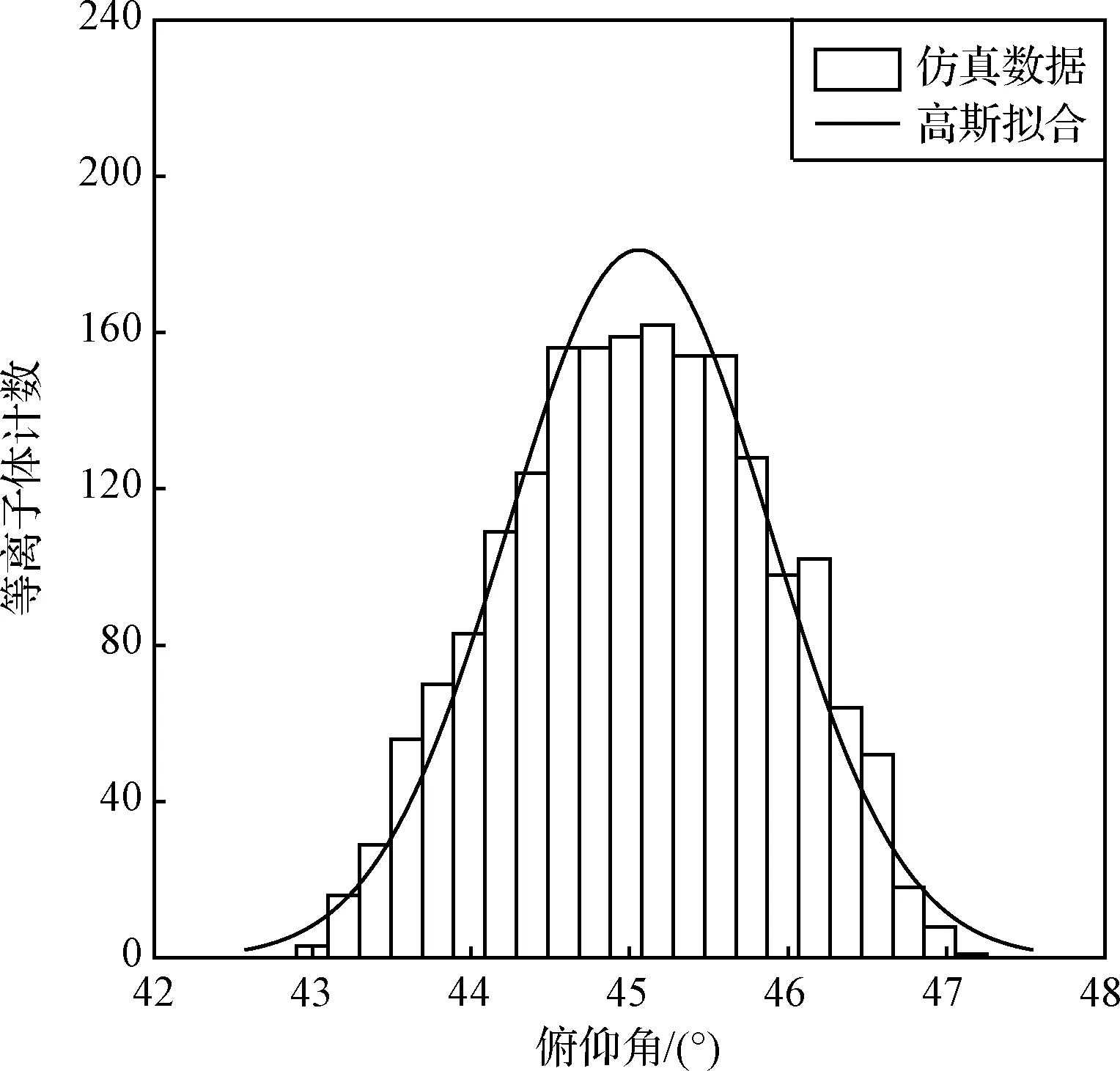
图5 入射俯仰角分布Fig.5 Incident elevation distribution
定义偏转板因子:
(3)
式中:Vupper、Vlower分别为上、下偏转电压。

图6 偏转板因子与俯仰角拟合曲线Fig.6 Fitting line between deflector factor S and elevation angle
图6为α随S的变化曲线,误差棒长度为俯仰角分辨率。多项式拟合方程为:
α=-113.6×S3+8.769×S2-90.17×S+44.78
(4)
方程的拟合确定系数为1,拟合结果可用于对各能量等离子体俯仰角的计算。
随着俯仰角由45°向0°或90°偏转,俯仰角分辨率逐步变差,图7给出了相近尺寸下的幂函数剖面偏转板和HPA采用的球形剖面偏转板的俯仰角分辨率的对比,结果显示HPA的视场偏转系统设计使俯仰角分辨率在0°和90°得到了明显改善,分别优化至为6°和5°。

图7 俯仰角分辨率随俯仰角的变化Fig.7 Elevation resolution at different elevations
随着俯仰角的变化,由于偏转板的遮挡,等离子体有效计数率会受到影响,图8给出了两种剖面偏转板的等离子体有效计数率响应对比,由图中曲线可得,HPA在0°和90°俯仰角附近的计数率仍维持在90%以上。
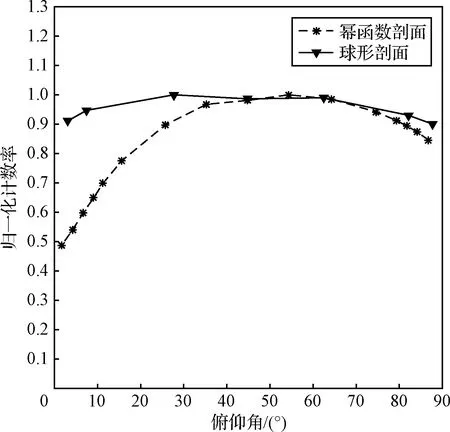
图8 归一化计数随俯仰角的变化Fig.8 Normalized counts at different elevations
综合以上比较分析,HPA的视场偏转系统设计有效改善了幂函数剖面偏转板带来的俯仰角分辨率变差和有效计数率下降的问题。
2.3 方位角视场与方位角分辨率
HPA呈旋转对称结构,方位角具有360°变化范围。球形静电分析器对入射等离子体束有聚焦作用,方位角分辨率定义为落在微通道板上的光斑与中心形成的圆心角。视场偏转电压为0 V时,方位角分辨率约为0.7°,优于单个扇形阳极7.5°的分辨需求。
俯仰角向0°和90°偏转时会影响方位角分辨率。图9给出了前述两种剖面偏转板设计的方位角分辨率随俯仰角的变化情况,比较两条曲线可知,HPA采用的球形剖面偏转板在0°俯仰角附近方位角分辨率仍维持5°左右,而相近尺寸下幂函数剖面设计的方位角分辨率接近7.5°;俯仰角靠近90°时,HPA方位角分辨率变化较平滑,在90°俯仰角附近将方位角分辨率由50°左右优化到35°,而且处于7.5° 方位角分辨率以内的俯仰角范围达到约74%,而幂函数剖面设计仅能使60%的俯仰角范围的方位角分辨率达到7.5°。

图9 方位角分辨率随俯仰角的变化Fig.9 Azimuth resolution at different elevations
2.4 几何因子
几何因子表征探测器接收粒子的能力,是衡量HPA测量灵敏度的重要参数。根据Vasyliunas等[23]和Chase等[24]的定义,几何因子G与计数率C和微分通量j有如下关系:
C=G·j
(5)
呈旋转对称的静电分析器G的表达式为[25]:

(6)
式中:T为面元dxdy内等离子体透过效率;Tdxdy为有效面积;β0为单个计算像素方位角,即7.5°。式(6)由积分式写成求和式:
(7)
式中:Δαi和ΔEj分别为俯仰角步长和能量步长,(Aact)ij为有效面积。
式(7)计算的G=2.2×10-4(cm2·sr·eV·eV-1),可以满足指标中对磁层热等离子体的探测需求。图10给出了1 keV入射源的等离子体计数率的分布,闭合曲线越靠近中心,等离子体计数率越大,最中间闭合曲线的等离子体计数率为100%,等离子体计数率最大值出现在能量1070 eV和俯仰角45°附近,与有效等离子体能谱和俯仰角分布一致。

图10 1 keV有效等离子体归一化计数率分布Fig.10 Normalized counts distribution of 1 keV plasma
HPA设计具有可变几何因子功能,由顶盖电极电压控制实现。顶盖加电压时,顶盖电场对入射等离子体产生抑制作用,通过静电分析器狭缝的等离子体通量降低,从而降低仪器几何因子。
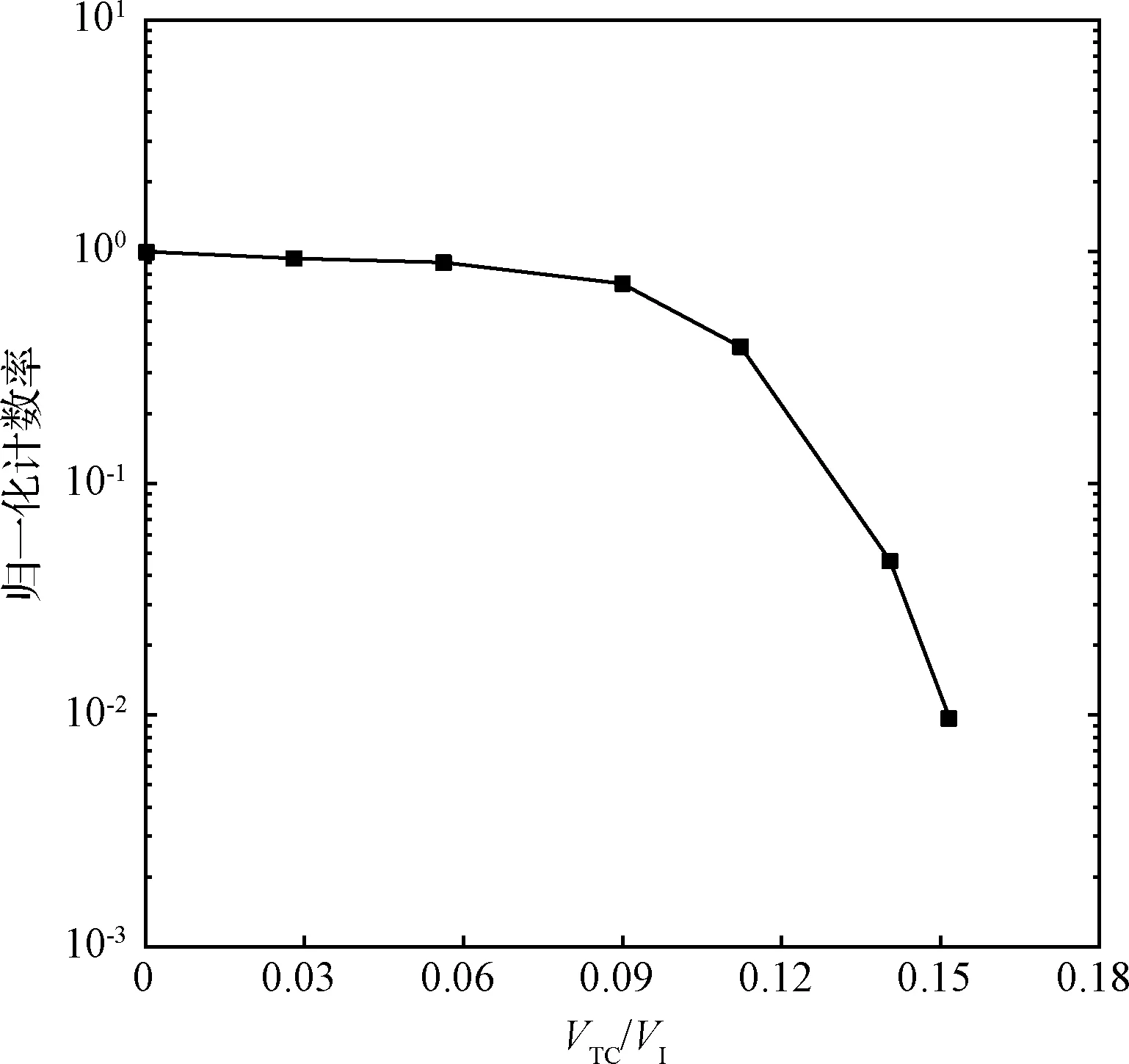
图11 可变几何因子响应曲线Fig.11 Variable geometric factor response
由式(5)可得,入射源相同时,j为常数,则G与C成正比。图11给出了有效等离子体归一化计数率随VTC/VI的变化曲线,VTC为顶盖电压值。从曲线得知,顶盖电极不需要很高的电压就可使几何因子降低两个数量级。VTC增加到VI的13%,几何因子可降低一个量级,当VTC增加到VI的15%时,几何因子就可降低两个数量级。
3 结 论
本文以三轴稳定卫星平台上的2π视场高分辨热等离子体探测需求为出发点,提出了一种新构型的仪器设计方案,提高了角度分辨率以及响应一致性。
HPA采用球形剖面视场偏转系统和高聚焦特性粒子光学系统优化设计,实现了单台仪器2π高分辨半球形探测视场,采用顶盖电压控制方式实现几何因子在两个量级内的连续可变,满足大通量动态范围热等离子体的全空间探测。表2给出了两种剖面构型的视场偏转系统的视场范围与分辨率的比对情况。由表2中数据可得出,经过球形剖面偏转板优化的视场偏转系统在保持全空间视场的同时,具有更高的俯仰角分辨率,实现了较大的高分辨率覆盖范围和较好的几何因子响应一致性,将高方位角分辨率覆盖范围提高到74%。HPA的视场偏转系统的各项优点为以后更高分辨率的仪器设计提供了支撑。

表2 两种视场偏转系统剖面构型探测视场的比对Table 2 FOV comparison between two different FDS
通过仿真分析,本文提出的热等离子体分析仪的设计方案满足预期指标需求。表3是仿真结果与HPA预期技术指标需求的比对,HPA各项参数均达到了探测指标要求。
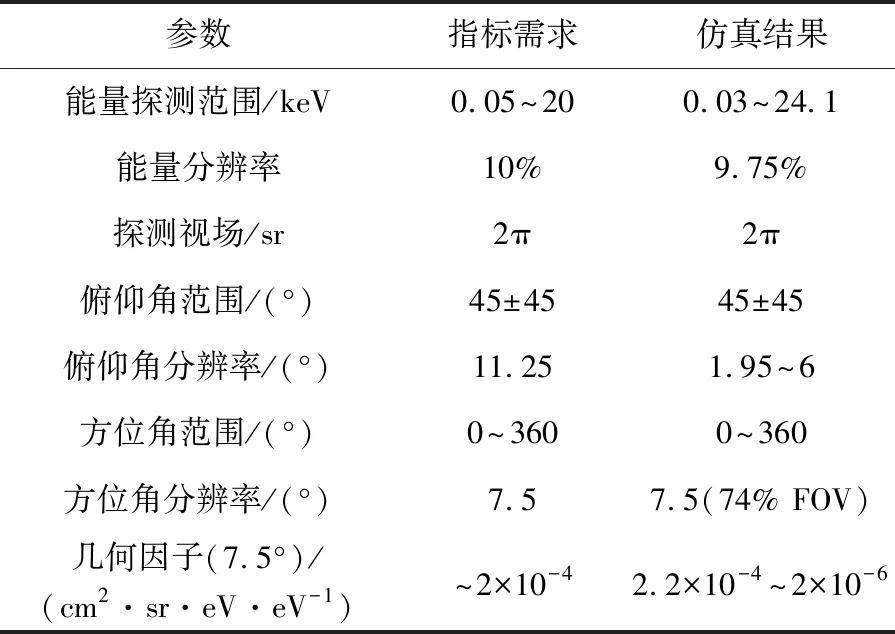
表3 仿真结果与技术指标需求的比对Table 3 Comparison between simulation results and requirements
