聚合物驱的机会约束规划最优控制
2019-06-04雷阳
雷 阳
(福建警察学院, 福建 福州 350007)
0 引 言
聚合物驱是指向油藏地层中注入聚合物水溶液,从而达到提高原油采收率的目的。由于聚合物的成本很高,为了获得最大的经济效益,必须确定合理的聚合物注入策略。国内外已经有学者利用最优控制理论或混合遗传算法研究石油开采中的最优注采方案问题,但求解过程中需要推导伴随方程等条件,计算量大并且推导过程复杂[1-3]。雷阳、张晓东等[4-5]应用混合遗传算法、控制向量参数化等方法对聚合物驱注采优化问题进行求解,得到了较好的效果。由于以上方法在求解中均假设油藏地质参数是确定的,而实际上,油气储层是非均质的,地质参数如油藏渗透率、孔隙度等都具有不确定性,油藏地质参数的不确定性会对聚合物驱开发带来一定的风险。
针对油藏地质参数的不确定性问题,文中基于机会约束规划方法建立了带有不确定参数的聚合物驱最优控制模型,提出了求解该模型的随机模拟遗传算法。为聚合物驱开发方案的制定提供了新的决策支持依据。
1 机会约束规划
机会约束规划可有效解决带有不确定性因素的随机优化问题,最早由Charnes等[6]提出。机会约束规划将带有不确定性因素的随机优化问题转化为某一置信水平下的确定性优化问题,最优决策满足约束条件的概率不小于该置信水平。对于复杂的机会约束条件,可引入Monte Carlo随机模拟技术进行处理[7]。
机会约束规划问题可描述为:
(1)
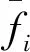
x----n维决策向量;
ξ----随机向量;
Pr{·}----{·}中事件成立的概率;
αj、βi----分别为给定的置信水平;
fi(x,ξ)----在保证置信水平至少为βi时取得的最大值[8-9]。
式(1)中,若m=1,则表示单目标机会约束规划。
2 聚合物驱最优控制模型
2.1 聚合物驱渗流物理方程
聚合物驱的渗流物理方程由油、水两相渗流方程和溶质组分的对流扩散吸附方程联立获得,描述水、油两相通过一维多孔介质的流动特征,方程中假设两种流体是不可压缩流体。以获取最大收益为目标,要求得聚合物的最优注入浓度,该最优控制问题可以表示为以下模型:
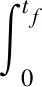

(2)
式中:Sw----含水饱和度;
fw----流体中水相流量分数;
t----注入流体占岩心孔隙体积的倍数(PV);
z----无因次长度坐标,z∈[0,1];
C----岩心中聚合物的质量浓度;
M、N----均为吸附参数,常数;
γ----常数;
φ----岩石孔隙度,由于储层的非均质性,其参数值具有不确定性,可以通过对测量数据统计分析确定其数值的近似分布规律;
Pe----Peclet数,其值与φ有关;
u----注入聚合物的质量浓度,即施加在边界上的控制量;
J----性能指标,产油收益减去聚合物成本,其中
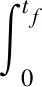
(3)
式中:g----聚合物驱用量。
J和g都经过无因次化处理。
模型初始条件和边界条件分别为:
(4)
式中:Sor0----已知初始残余油饱和度;
Sor----残余油饱和度。
在聚合物驱的注入过程中,通常采用分段注入的方式,注入浓度可以表示为如下的分段函数形式:
(5)
式中:P----段塞数;
ui----各段塞的注入浓度,即所要求解确定的控制量。
求解模型还需要水相流量分数、相对渗透率、聚合物溶液粘度等参数。
水相流量分数:
(6)
式中:kro、krw----分别为油相和水相相对渗透率;
μo、μw----分别为油相和水相粘度。
相对渗透率:
(7)
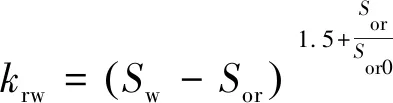
(8)
聚合物溶液粘度
μw=μw0(1+ap1C+ap2C2+ap3C3)
(9)
式中:μw----纯水的粘度,mPa·s;
ap1,ap2,ap3----粘度系数。
2.2 不确定参数下的聚合物驱最优控制模型
在不确定的环境下做出的开发决策自然会有一定的风险,其结果是达不到预期开发效果或收益损失可能增加,因而需要对相应的风险进行规避,制定兼顾收益和风险的聚合物驱开发策略。记ξ为随机参数向量,表示模型中具有随机特性的不确定参数;u为控制量,即注入聚合物的浓度;考虑聚合物的用量约束,从而带有机会约束的不确定参数下聚合物驱注入策略优化模型可描述为:
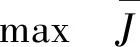
(10)
式中:g0----聚合物的最大用量;
β----置信水平;
umin,umax----分别为每个段塞聚合物注入的最小、最大浓度;
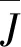
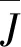
式(10)以在一定概率下可能实现的目标收益最大化为优化目标,通过优化计算求得最优聚合物注入策略。式(10)中的随机约束条件等价于:
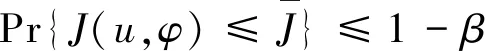
(11)
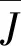
由于聚合物驱最优控制模型的支配方程由偏微分方程组描述,转化为确定性问题极为复杂,因此提出一种基于随机模拟的遗传算法进行求解。
3 随机模拟的遗传算法求解步骤
3.1 随机模拟
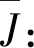
1)从概率分布Φ(ξ)中产生N个独立的随机向量{ξ1,ξ2,…,ξN};
2)计算Ji=J(u,ξ),i=1,2,…,N;
3)对βN取整,即N′=[βN];
3.2 遗传算法求解步骤
遗传算法是一种通过模拟自然进化过程搜索的全局智能优化方法[10],为解决复杂机会约束规划问题提供了有效途径。对于计算过程中可能产生不可行解,文中将惩罚函数引入到目标函数中,不可行解存活的概率大大降低[11]。
针对不确定参数下聚合物驱注入策略优化问题,利用基于随机模拟的遗传算法的求解步骤为:
1)给定初始置信水平β;
2)初始化种群规模NP、最大循环次数NG、交叉概率Pc和变异概率Pm;
3)随机产生NP组初始控制量u;

5)对控制量u进行交叉和变异操作;
6)采用轮盘赌法正比选择控制量u;
7)是否达到最大循环次数,未达到则返回4);
4 不确定参数下的优化模型求解
以聚合物驱五段塞注入方式(P=5)对注入方案进行优化求解。设t0=0,tf=2,时间节点t=[0.05,0.1,0.2,0.3,0.4],各段塞注入浓度为常数,设u=[u1,u2,u3,u4,u5],且umin=0,umax=2.5,其他参数取值见表1。
记ξ=φ,设岩石孔隙度服从正态分布,即φ~N(μ,σ2),φ∈[0,1],其均值μ=0.5,方差σ2=0.152。设定置信水平β=0.8,聚合物最大用量g0=0.6,采用基于随机模拟的遗传算法进行求解。设定随机模拟次数N=400,种群规模为NP=10,交叉概率Pc=0.8,变异概率Pm=0.1,经过NG=10次循环得到最优结果为:
u=[1.528 4,2.405 0,2.295 0,0.250 0,1.156 7]
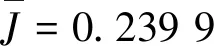
经验证,在最优控制量u时,不确定参数下的性能指标J满足概率约束,即
Pr{J(u,φ)≥0.239 9}≈0.8
所得到的最优解满足机会约束条件。
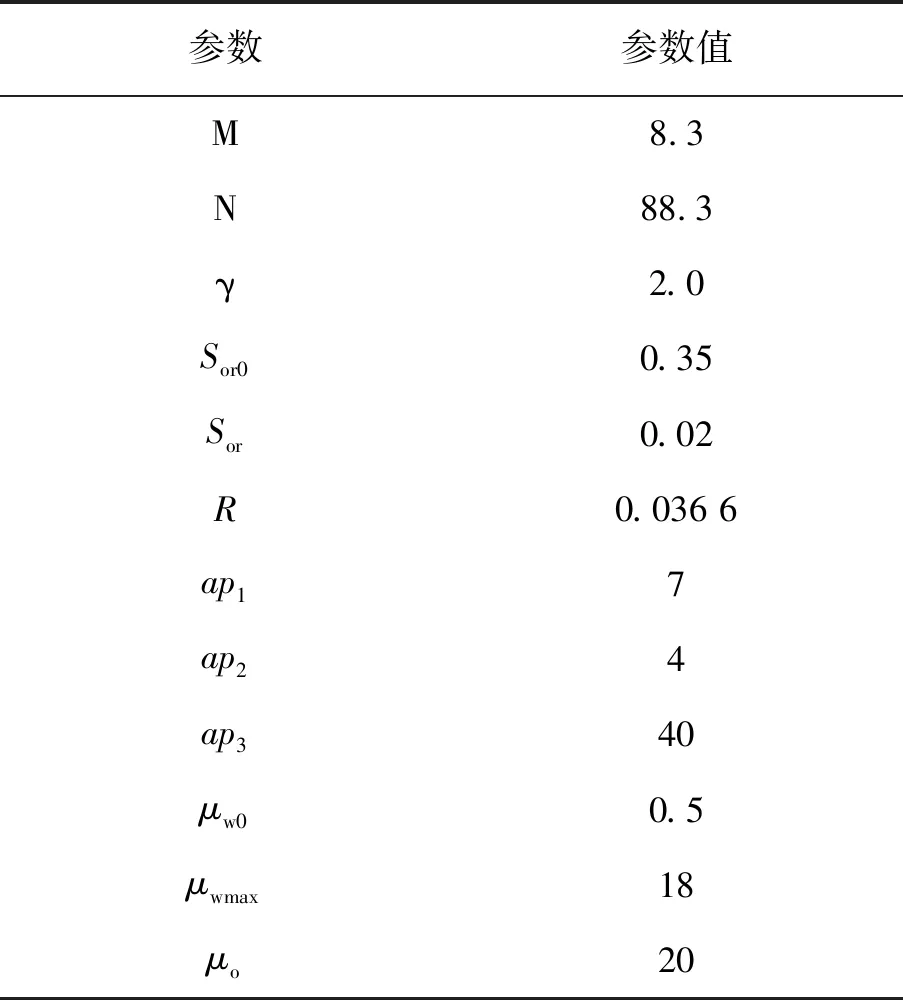
表1 求解聚合物驱模型所需参数
保持其他参数不变,分别取不同的置信水平β,计算结果见表2。
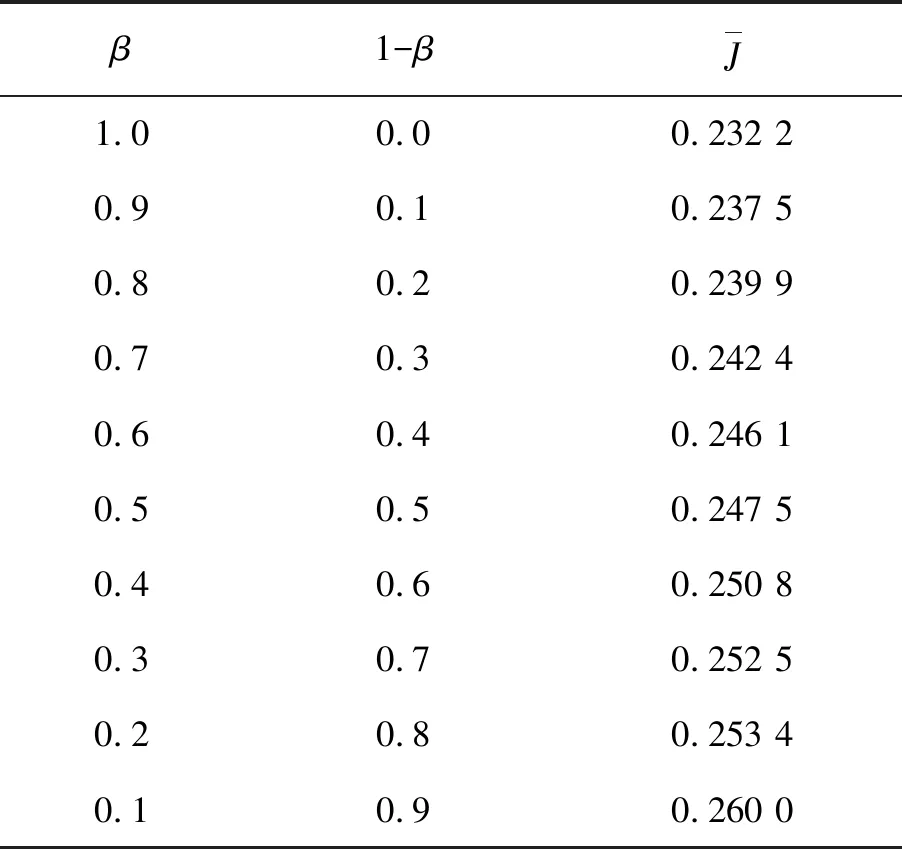
表2 不同置信水平β下的最优性能指标
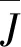
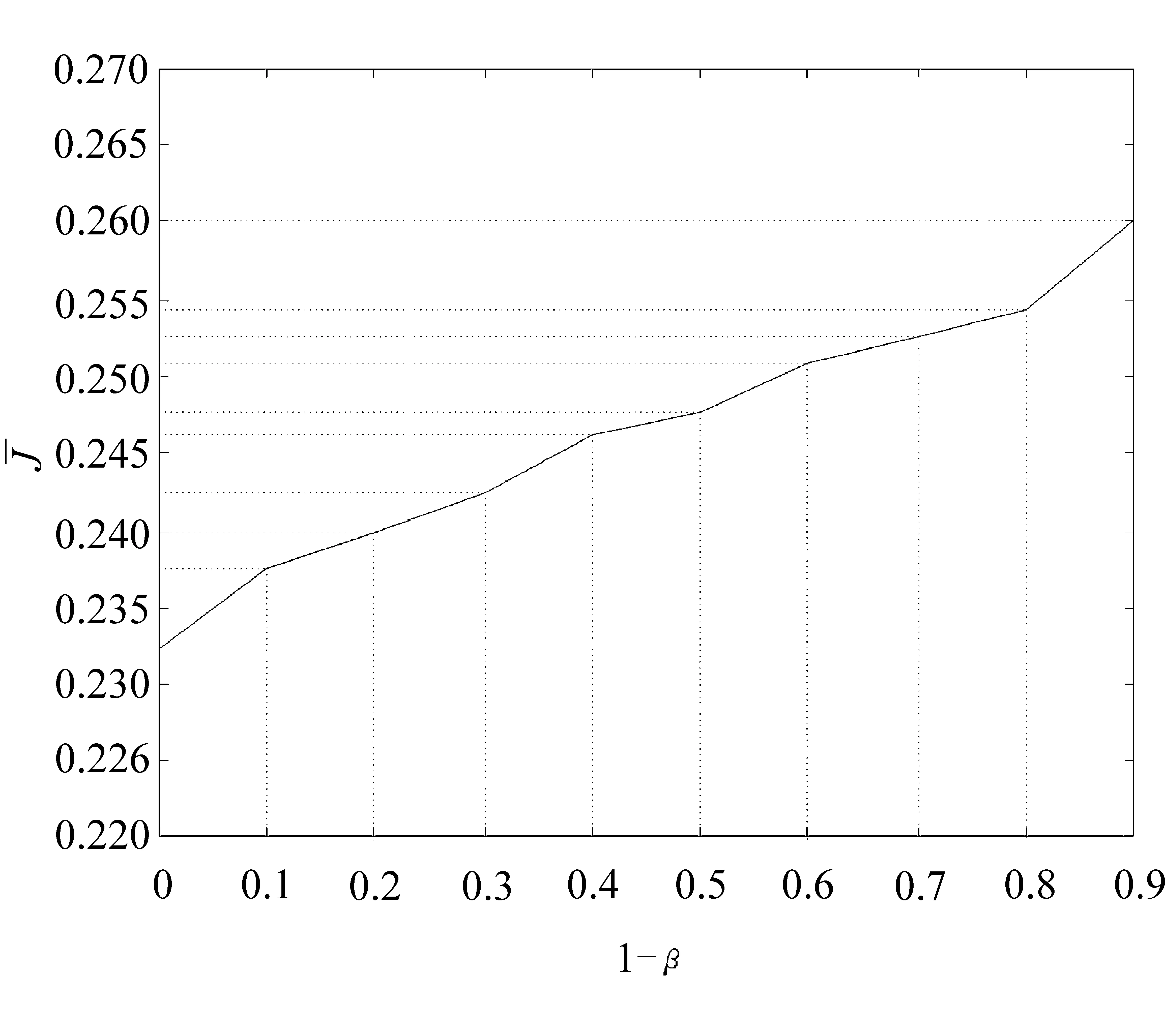
图1 不同风险下的目标收益曲线
结果表明,在不确定参数下,决策者所能承受的实际收益小于目标收益的概率(1-β)越大,则风险越大,获得的收益也越大,即高风险则高收益。
5 结 语
建立了不确定参数下的聚合物驱注入策略优化模型,采用机会约束规划方法进行求解,为聚合物驱开发评估风险提供了一条新途径。在不同的置信水平下,可获得的最大收益情况不同,置信水平越低,风险越大,则可获得的最优收益也越大。
文中所建立的具有不确定参数的风险-收益模型仍假设原油价格不变,而实际上原油价格是不断变化的,下一步工作将对原油价格进行合理预测,并考虑更多的不确定因素,使模型能够更符合实际。
