水深对机枪密封式膛口流场影响的数值分析
2019-06-04张欣尉余永刚
张欣尉,余永刚
(南京理工大学 能源与动力工程学院,南京210094)
0 引言
枪炮水下发射时,水的密度约为空气密度的800 倍,为保证发射安全性和威力,Stace 等[1]提出了水下密封式发射,即在膛口加装密封装置,当弹前空气压力达到某一数值时密封装置打开,随后弹丸运动出膛。密封式发射时,膛口周围水介质将对弹丸运动和燃气射流的扩展产生较大影响,针对水深变化对密封式发射膛口流场影响的研究对于水下枪炮的研究具有一定理论意义和工程价值。
膛口流场对弹丸运动以及周围环境均具有重要的影响作用,对于枪炮在空气中发射所形成的膛口流场,国内外专家学者开展了大量研究工作。Klingenberg 等[2]对7.62 mm 步枪膛口焰及温度进行了测量。Jiang 等[3]针对马赫数为3.0 的高速射弹的膛口流场进行了数值模拟,捕捉并详细分析了其波系特征。吴伟等[4]基于无网格算法再现了膛口流场中膛口初始冲击波、膛口冲击波、欠膨胀射流波系结构的动力学发展过程。Zhang 等[5]和Florio[6]分别从实验和数值模拟方面研究了炮口制退器结构对膛口流场的影响。水下密封式膛口流场还涉及到高温高压燃气射流水中扩展,而对于高温高压燃气射流的研究已经十分丰富。Xu 等[7]基于volume of fluid(VOF)多相流模型对水下火箭喷管高速燃气射流进行了数值模拟。莽珊珊等[8]对充液室边界形状对圆形射流扩展的影响进行了实验和数值研究。唐云龙等[9]采用VOF 模型对水下高速欠膨胀燃气射流的结构及推力特征进行了研究。Xue 等[10]对双股燃气射流在阶梯状充液室内的扩展进行了实验研究和数值分析,发现直径增量与孔间距的比值大于0.6 时有利于射流的汇聚和径向扩展。Zhou 等[11-12]和Hu 等[13]对多股燃气射流在圆管内的扩展进行了实验和数值研究,两者采用不同喷孔结构对水下枪炮气幕式发射过程中的多股射流协同排水效果进行了对比分析。
目前,对于水下枪炮密封式发射的研究仍较少,刘育平等[14]对水下炮密封式发射的内弹道过程进行了数值计算,发现膛压升高而初速降低,并捕捉到了膛口内部激波。对水下枪密封式膛口流场的研究更为少见,本文数值模拟了3 种水深条件下的密封式膛口流场,重点讨论了水深对密封式膛口流场的影响,对水下密封式发射枪炮的研究具有一定参考意义。
1 数理模型
VOF 多相流模型被广泛地应用于对水中燃气射流的研究[8-12],本文同样采用该模型对膛口燃气射流进行数值模拟。
1.1 物理模型
根据水下枪炮密封式发射特点,对12.7 mm 滑膛式机枪水下密封式膛口火药燃气流场,采用以下简化假设:
(1)膛口燃气射流的扩展看作是一个非稳态过程,近似处理为二维轴对称问题;采用k-ε 模型模拟流场中气液湍流作用。
(2)膛口燃气射流近似处理为可压缩理想气体射流,不考虑燃气射流的组分变化,并忽略其体积力的影响。
(3)不考虑枪口附近水的相变以及空化的影响。
数值计算中多相流模型采用VOF 模型,湍流模型采用标准k-ε 模型。利用PRESTO! 方法对压力项离散,动量和能量的离散采用一阶迎风格式,压力与速度耦合采用PISO 算法,计算过程中时间步长控制在0.2 μs 以内,以保证计算稳定性。
1.2 数学模型
根据1.1 节物理模型,对燃气射流建立以下数学模型:
(1)连续性方程

式中:ρq表示密度,q=1,2 分别表示气、液两相;α1和α2分别表示气液各相的体积分数,且α1+α2=1;υ为速度矢量。
(2)动量方程:

式中:气液混合密度ρ=α2ρ2+(1- α2)ρ1;ρ 为压强;μ 为粘度系数。
(3)能量方程:

(4)气体状态方程:

式中:R 为理想气体常数,R=8.314 J / (mol·K)。
(5)k-ε 湍流方程:
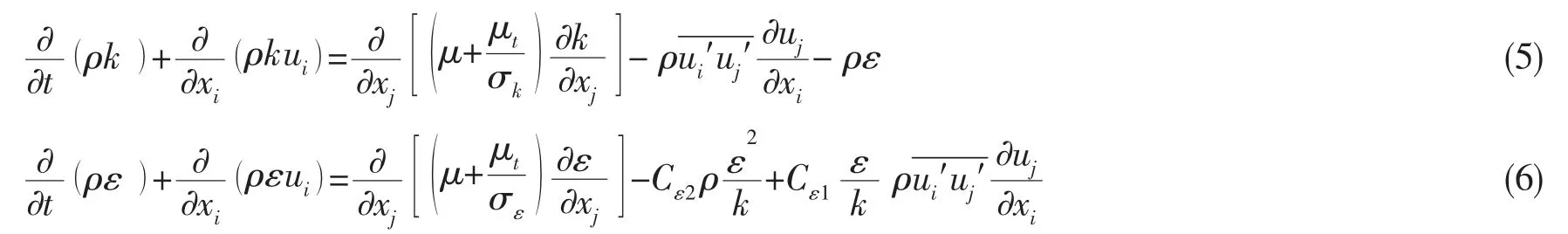
式中:k 和ε 分别为湍动能和耗散率;常数σk=1.0 和σε=1.3 分别为湍动能与耗散率对应的Prandtl 数;μt=Cμk2/ε 为湍流粘性系数,xi和xj为坐标矢量;ui和uj为为速度矢量;i 和j 为自由指标;常数Cε1=1.44、Cε2=1.92 和Cμ=0.08 为经验系数。
1.3 数理模型的实验验证
本研究对文献[8]中圆形燃气射流在圆柱形充液室内扩展的实验进行了数值模拟,图1 为数值模拟和实验中射流头部轴向最大位移与时间的关系对比图。由图1可知,数值模拟结果与实验结果吻合较好,最大误差仅为2.8%,说明本文所采用的数理模型是可信的。
2 边界条件与计算模型
针对计算需求,对计算域进行以下划分:弹后燃烧室、身管和膛口周围区域。

图1 射流头部轴向最大位移与时间的关系Fig.1 The relationship between the maximum displacement of the jet head and the time
2.1 网格划分
本节给出了水下密封式发射计算模型,如图2所示,其中图2(a)为计算模型示意图,图2(b)为计算域网格示意图。由图2(a)显示,计算分三个区域,Ⅰ区为弹后燃烧室,Ⅱ区为弹前身管内部,Ⅲ区为膛口周围流场,膛口流场计算区域取长为0.7 m、半径为0.2 m 的圆柱形区域。由图2(b)显示,计算域采用结构化和非结构网格,最小网格尺寸为0.25 mm×0.25 mm,位于Ⅲ区弹丸运动区域,即枪口至出口边界间长0.5 m、半径0.006 35 m 的圆柱形区域。在图2(a)中,O 点为膛口中心,以其为参考零点,P 点坐标为(100 mm,19.05 mm)。
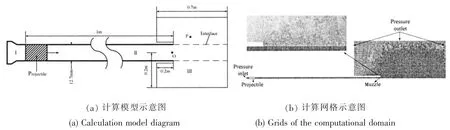
图2 水下密封式发射计算模型Fig.2 Computational model for underwater sealed launch
2.2 边界条件
燃烧室设为压力入口,弹丸定义为运动刚体,膛口流场计算区域外边界为压力出口边界,初始化为环境变量参数,即水深为1 m 时初始压力为111 325 Pa,水深50 m 时初始压力为601 325 Pa,水深100 m 时初始压力为1 101 325 Pa;忽略水深对温度的影响,即初始温度均取300 K。
2.3 网格无关性验证
考虑到动网格的分裂与合并,最小网格尺寸设定为0.25mm×0.25mm,对膛口周围流场(Ⅲ区)进行不同尺寸网格加密设置,分别得到21.5 万、17.9 万和13.4 万网格数的计算网格。由于图2(a)中P 点会经历气液相态转变及射流夹断等复杂变化,故选其进行网格无关性验证具有一定代表性。以三种网格数下的P 点压力随时间变化为参考,如图3所示。图3 显示,与21.5 万网格数下P 点压力相比,采用17.9 万网格数进行计算时平均误差为4.8%,而采用13.4 万网格数进行计算的平均误差达到16.1%,为保证计算精度和计算效率的最优配置,本研究采取17.9 万网格进行数值计算。
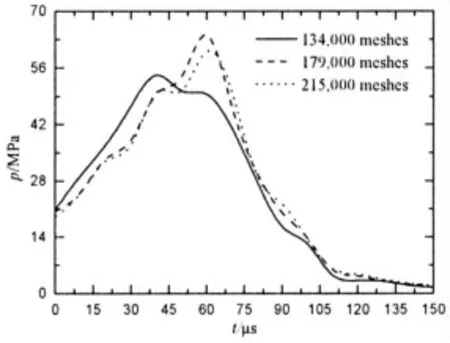
图3 采用不同网格数计算的参考点压力-时间对比Fig.3 Pressure-time curves of reference point under different grids
3 结果与讨论
通过数值模拟,对滑膛式机枪在不同水深条件下密封式发射的弹道结果和膛口流场特性进行了分析,弹丸口径为d0=12.7 mm、弹丸长度为l0=50 mm,膛口密封膜片打开条件为内外压力差Δp=105Pa。
3.1 弹道结果
由计算可知,随着水深增加,枪口初速降低明显,最高膛压略有升高,内弹道参数见表1。同时给出了不同水深条件下弹丸出膛后的膛外行程对比曲线,见图4,由图可知,水深越大弹丸运动越慢,且随着弹丸速度降低,速度衰减将加快。

表1 内弹道参数Tab.1 Interior ballistics parameters
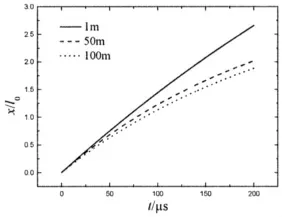
图4 不同水深下弹丸膛外行程Fig.4 Projectile displacement out of muzzle under different water depths
对弹丸行程随时间变化特性进行拟合,发现其在不同水深条件下均满足指数函数规律,即:
x(t)=x0+x1e-t/t1
式中:x(t)为弹丸膛外行程;t 为时间,s;x0,x1和t1为弹丸膛外行程随时间变化的拟合参数,如表2所示。
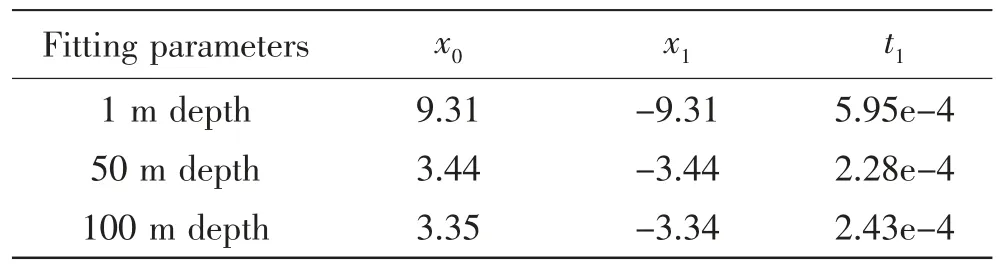
表2 弹丸膛外行程随时间变化的拟合参数Tab.2 The fitting parameters for the displacementtime curves of the projectile
3.2 膛口流场
通过数值模拟,得到了12.7 mm 机枪水下密封式膛口流场分布情况,图5-7 分别为1 m、50 m 和100 m 水深条件下的膛口温度场和速度场分布云图。

图5 1 m 水深条件下膛口温度场和速度场分布Fig.5 Distribution of muzzle temperature and velocity field under 1 m depth condition
由图5-7 中射流边界可知,相同时刻,水深越大射流径向扩展越大,而轴向扩展越小,这是因为水深较大时弹丸初速较低且衰减快,弹丸运动距离较近,不利于燃气轴向扩展,从而导致燃气射流径向扩展明显。由温度场与速度场分布可知,水深越大,波系核心区分布区域越小,这是受环境压力的压缩作用影响;比较相同时刻燃气射流速度场分布可知,水深较小时燃气射流扩展速度更快,这也印证了气体空腔和波系核心区分布大小规律。3 种水深条件下,燃气出膛经过膨胀区后被压缩产生高温气团,随着时间推移,高温气团向下游运动,随后新的高温气团产生;在1 m 和50 m 水深条件下,高温气团逐渐被压缩,分布范围缩小而温度升高,而100 m 水深条件下的高温气团移动较慢,从70 μs 到200 μs,分布区域变化不大;观察可知,水深越大,高温气团向下游移动也越慢,燃气集聚在离膛口更近的位置。


图6 50 m 水深条件下膛口温度场和速度场分布Fig.6 Distribution of muzzle temperature and velocity field under 50 m depth condition
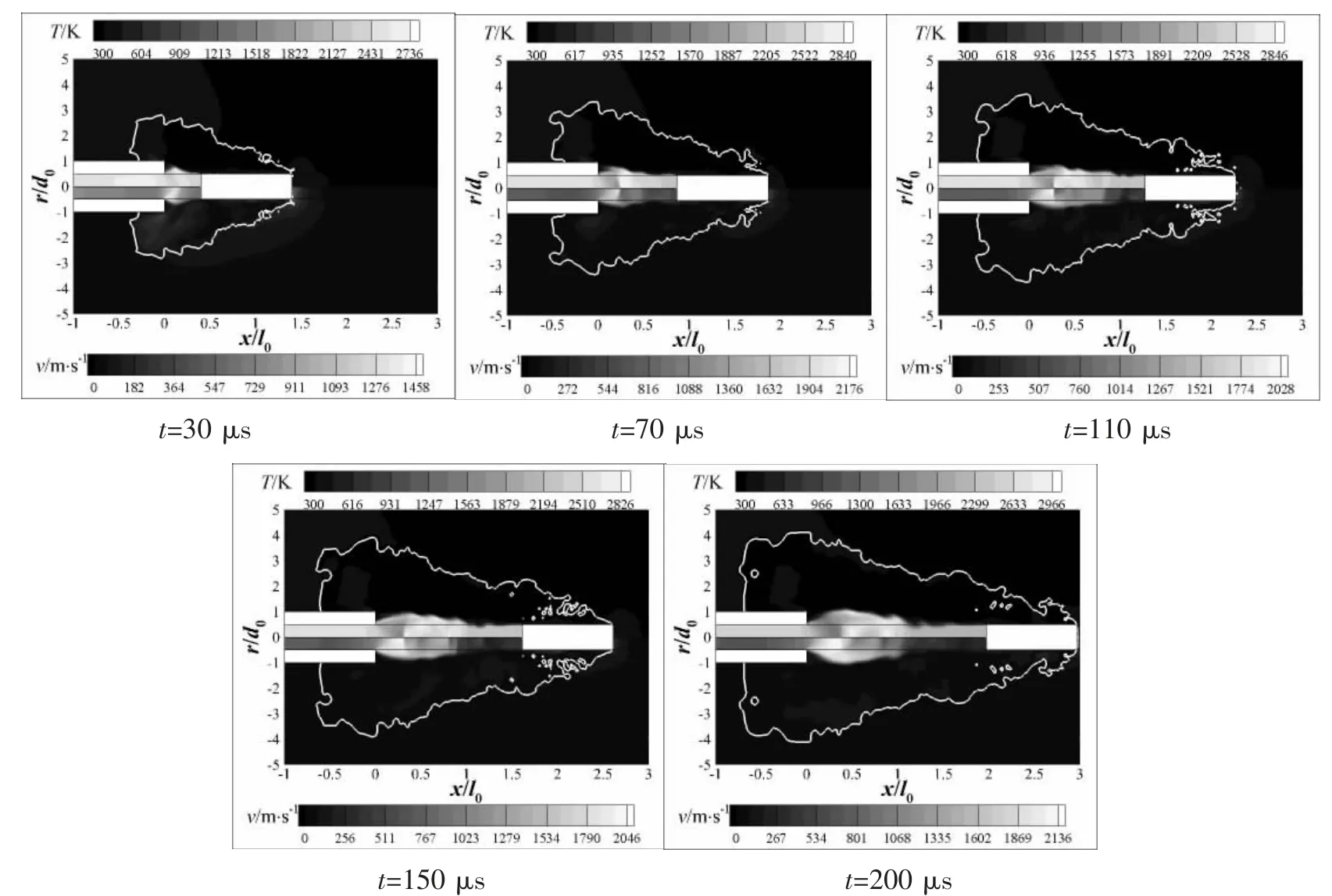
图7 100 m 水深条件下膛口温度场和速度场分布Fig.7 Distribution of muzzle temperature and velocity field under 100 m depth condition
同时,由图5-7 中温度云图可以发现,3 种水深条件下最高温度的出现时刻均比较靠后,出现位置逐渐靠近膛口,说明密封式膛口流场演化及分布具有一定规律性。为了进一步了解流场中温度分布和马赫盘位置,图8给出了3 种水深条件下膛口至弹底中心温度沿轴向分布曲线。
由图8 可以发现,3 种水深条件下,马赫盘结构在70 s 时刻均已形成,但随着水深增大,马赫盘位置离膛口越来越近。燃气射流在膨胀区头部,即马赫盘位置达到最低温度:200 s 时刻,1 m 水深条件下,最低温度约为900 K;50 m 水深条件下,最低温度约为1 325 K;100 m 水深条件下,最低温度超过1 500 K;由此可见,随着水深增加,燃气射流膨胀区缩小,马赫盘位置更靠近膛口,但激波膨胀区内最低温度却升高。由图8 中200 μs 温度曲线可知,燃气射流在越过马赫盘后温度出现多次波动,1 m水深时温度出现4 个波动峰值,50 m 水深时温度出现3 个波动峰值,100 m 水深时温度出现2 个波动峰值。结合图5-7 中200 μs 时刻的温度云图可以发现,随着水深增加,弹丸运动距离较近、燃气射流速度也降低,使得高温气团的演变减慢,从而导致燃气在越过马赫盘后的压缩-膨胀次数减少,温度波动减弱。

图8 膛口-弹底中心温度沿轴向分布Fig.8 Temperature distribution along the axis from muzzle center to projectile base
4 结论
通过对12.7 mm 滑膛式机枪水下密封式发射的数值模拟,发现水深对弹道结果和膛口流场的演变具有一定规律:(1)水深增大,弹丸初速降低,速度衰减随速度降低加快,射流轴向扩展减缓而径向扩展加快;(2)不同水深条件下,弹丸膛外行程均满足指数变化规律;(3)水深增大,燃气射流激波核心波系区域减小,同时激波膨胀区被压缩,马赫盘位置离膛口距离更近;相同时刻,燃气在马赫盘位置温度更高而速度更低;(4)200 μs 时刻,随着水深增加,燃气射流在越过马赫盘后出现压缩-膨胀次数减少、温度波动减弱。本文结论对水下枪炮的设计具有一定参考价值。
