不同舰船机库外形下艉流场特征数值模拟研究

荣吉利，王 超，赵 瑞，李海旭，严 昊

（1.北京理工大学 宇航学院力学系，北京100081；2.中国船舶工业系统工程研究院，北京100036）

0 引言

舰载直升机在执行海上补给、搜救、反潜等任务中表现出巨大的优势，因此越来越多的舰载直升机被装备于非航空型舰船上。但与陆基直升机不同，由于舰船运动以及艉部流场结构复杂等因素，使直升机起降受到严重的影响[1-3]。当气流流经舰船会形成湍流边界层，随后会与飞行甲板前方的机库壁面发生碰撞，由于几何形状的突然变化，会导致流动发生膨胀，此时湍流边界层在机库的分离点处分离，形成自由剪切层，在机库后方的飞行甲板处形成巨大的回流区，该回流区包含了随时间变化的涡结构，且具有极强的非定常特性[4-6]。

相关学者使用计算流体力学（CFD）对影响舰船艉流场的因素进行了数值模拟研究。黄斌等人[7]通过建立一个基于NS 方程的舰载直升机着舰域流场分析方法，探究了机库开合状态对舰船艉部着舰域的影响，研究结果表明打开机库门更有利于直升机安全着舰；洪伟宏等人[8]以LHA 两栖攻击舰作为参考通过CFD 定常计算研究发现，舰船的上层建筑是诱发舰船舰面空气湍流的因素之一，而岛式上层建筑靠前的舰船可以改善后部甲板的流场环境；但国外相关的计算流体力学技术研究表明，时间精确的非定常计算能够精确捕捉由舰船船体结构产生的非稳态湍流气流[9-11]。赵瑞等人[12]通过高精度的DES 方法对SFS 与SFS2 等船型展开非定常数值模拟，得到了详细的船体流场涡脱落和时间精确的流场数据，并从数值上探究了有无上层建筑与机库门开合状态对艉流场的影响；刘长猛等人[13]使用FLUENT 的非稳态标准k-ε 模型进行计算，发现机库的形状与尺寸会对飞行甲板周围涡旋的强度和位置产生影响。

由此可见，舰船艉部空气流场的变化取决于诸多因素，其中类似后台阶类型的舰船艉部会因为机库外形尺寸的不同对其流场产生一定的影响。本文使用基于一方程SA（Spalart-Allmaras）模型[14]的脱体涡模拟（Detached-Eddy Simulation，DES）[15]对典型护卫舰船型进行数值模拟，研究了不同机库外形对艉流场的影响，并且根据非定常计算结果推导了预测艉流场回流区范围的经验公式。

1 计算模型与方法

1.1 计算方法

1.1.1 Spalart-Allmaras 湍流模型

基于一方程SA 模型的DES 方法，其湍流模型求解有关涡粘性变量的偏微分方程为：

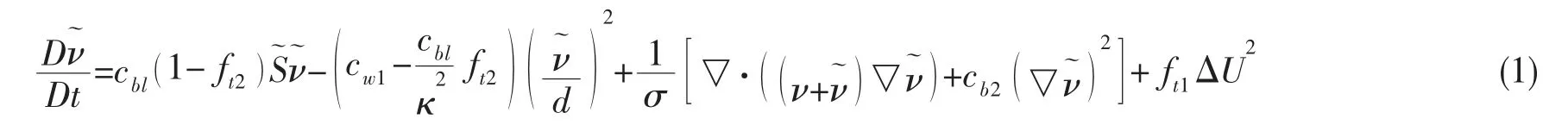
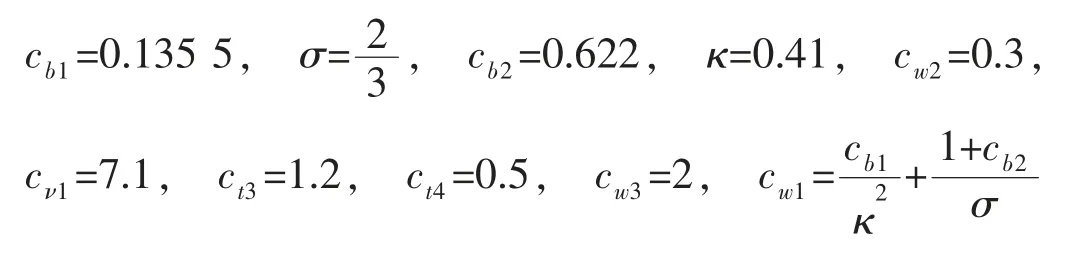
1.1.2 DES 模型

DES 方法是将大涡模拟（LES）方法和雷诺平均（RANS）方法相结合的湍流模拟方法，通过对Spalart-Allmaras RANS 湍流模型进行修正，使在离壁面近处的区域采用RANS 方法模拟边界层内小尺度涡的运动，而在远离壁面的区域处采用LES 方法模拟，对小尺度涡采用亚格子模型模拟，对大尺度涡进行直接模拟。通过结合LES 方法和RANS 方法的优点，DES 方法可以有效处理边界层内小尺度涡的脉动，同时也降低了计算资源和计算时间[16]。

在DES 方法中，SA 模型中的长度尺度，即流场中任意点到最近物面的距离d，用d~来代替，其中d~表达为

在当前计算中，Δ=max（Δx，Δy，Δz）为网格中心到相邻单元中心距离中最大的一个，CDES=0.65。其他细节可以参考文献[15]。

1.1.3 计算设置

本文通过CFD++软件，采用有限体积法对控制方程进行离散，并基于具有空间二阶精度的多尺度TVD（Total Variation Diminishing）限制器。时间推进采用具有二阶精度的双时间步长（Runge-Kutta）全隐式算法。定常计算采用一方程SA 模型并将其计算的结果作为非定常湍流计算的初始流场。非定常计算3 000 步，其中时间步长Δt*=1.88×10-2s。

1.2 几何模型

为了研究不同机库外形对舰船艉部流场的影响，并且减少计算资源的消耗，本文使用三种简化的护卫舰CFD 模型，如图1所示，分别命名为A 船、B 船与C 船。三种简化船型在外形和尺寸上均保持一致，仅对艉部机库的外形进行改动。其中，A 船机库横截面为“口”字型，机库高度6.5 m；B 船机库横截面为“凸”字型，最大机库高度6.5 m，最小机库高度4.5 m；C 船机库横截面为“口”字型，机库高度较低，为4.5 m。

图1 三种简化船型A 船（左）、B 船（中）与C 船（右）及其尺寸细节Fig.1 Dimensions of three simplified frigate ships

1.3 网格划分

整套网格为圆柱形区域，如图2所示，船体模型被放置于圆柱形区域的中央，半径r=4.5ls，高d=0.75ls，其中ls为船长。本文对三种简化模型采用混合网格进行划分，该混合网格由两部分组成：一是整个流场的非结构网格，船体表面利用三角形单元形成的40 层棱柱结构（垂直于壁面的第一层网格高度为5 mm，保证y+=o（10），增长率为1.3）来保证粘性层流动的捕捉；二是艉部飞行甲板上方区域的结构网格，根据Spalart 的“重点区域”理论[17]，为了能充分地发挥DES 方法的优点，网格单元应该尽可能地小并且各向同性，故在艉流场重点关注区域处使用结构网格能更好地控制网格的精细程度。网格细节图如图3所示。A 船、B 船与C 船的网格量分别为1 278 万、1 240 万和1 217 万。

图3 网格细节Fig.3 Details of simplified frigate ships’ grid

2 计算方法验证

为了准确地研究舰船艉流场特性并验证CFD 的计算效果，国际项目TTCP[18]得到了简化的护卫舰船型SFS2，其模型及尺寸如图4所示。加拿大国家研究委员会对两个简化模型都做过一系列的风洞实验，得到了飞行甲板及前部上层建筑中特定位置的平均速度场及湍流数据[19-20]。

为了验证本文CFD 方法的有效性，以SFS2 模型作为标准算例，针对0°风向角下的流场进行了计算。图5给出了艉部甲板上方直线的时均速度分布曲线与风洞实测数据的对比，该直线与机库等高度，位于甲板y-z 平面内正中间位置，横坐标为坐标值与甲板宽度d 的比值，纵坐标为速度分量u、v、w与来流速度U∞的比值。从图5 中可以看出本文的计算结果总体上与风洞实测数据相吻合，这表明本文采用的计算方法是有效的。

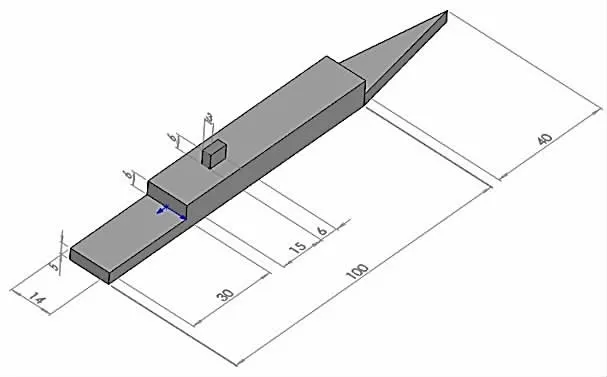
图4 SFS2 模型及尺寸细节Fig.4 The geometry of SFS2 and its dimensions

图5 0°风向角计算结果对比Fig.5 Headwind mean velocities normalized by U∞

3 不同机库外形对舰船艉流场的影响

机库的几何形状是影响艉流场回流区的重要因素之一，保证船体整体尺寸外形一致，探究不同机库纵截面外形对艉流场的影响。

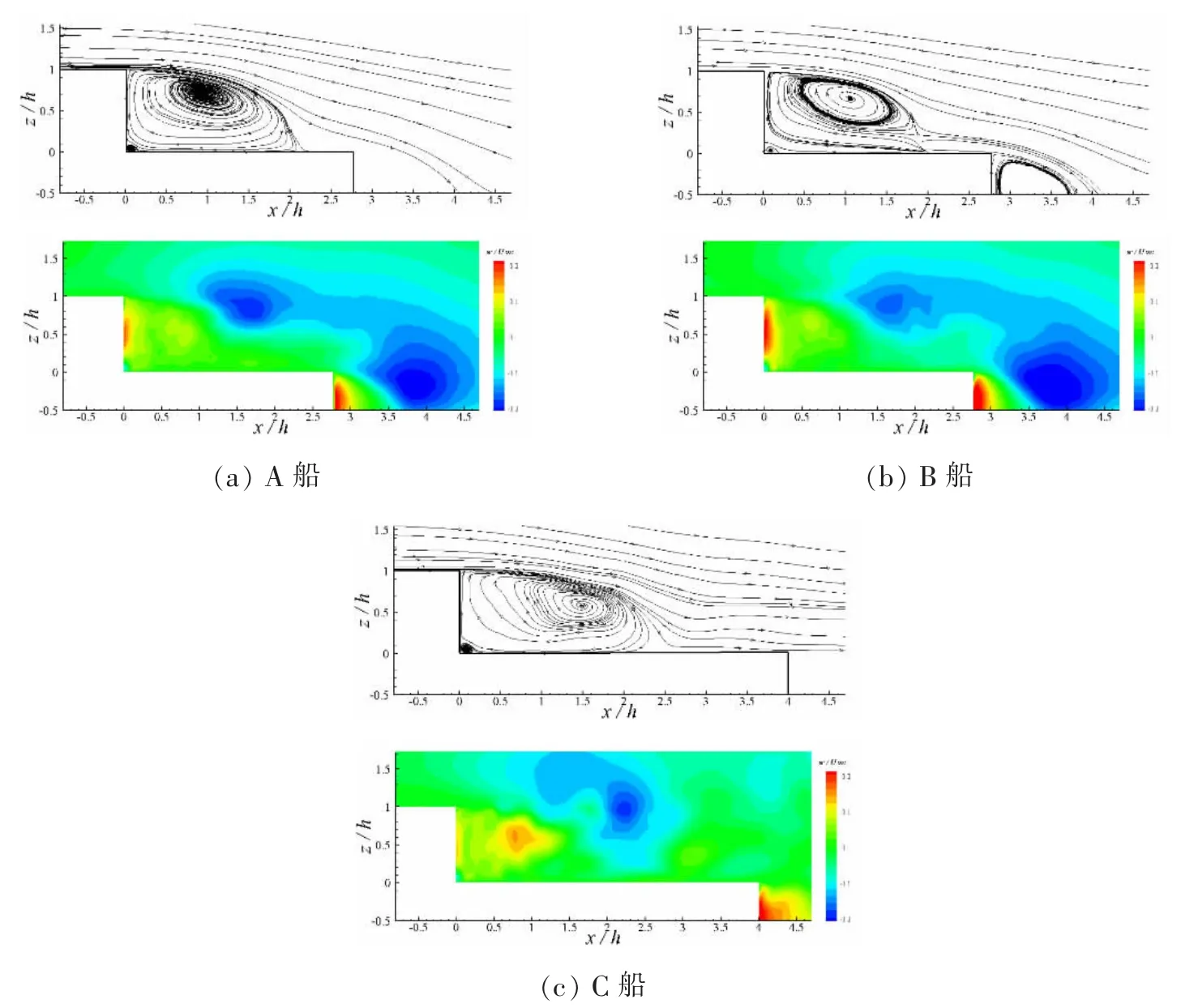
图6 0°风向角下y/b=0 截面处速度云图与流线图Fig.6 Streamlines and velocity magnitude contours for a headwind

图6 为0°风向角下y/b=0 截面的速度流线图与云图。从图中可以看出，A 船回流区纵向长度约为2.05 倍机库高度，B 船回流区纵向长度约为1.95 倍机库高度，C 船回流区纵向长度约为2.27 倍机库高度。回流区范围差距不大，直升机着舰域均在回流区内。但从速度云图可以明显看出，B 船飞行甲板上方的下洗速度要明显小于A 船；在飞行甲板长度相同的情况下，A 船与B 船回流区纵向长度占据了整个甲板的约74%，而C 船约为57%；从速度云图也可以看出C 船回流区更靠近机库，直升机着舰域位于回流区边缘处。

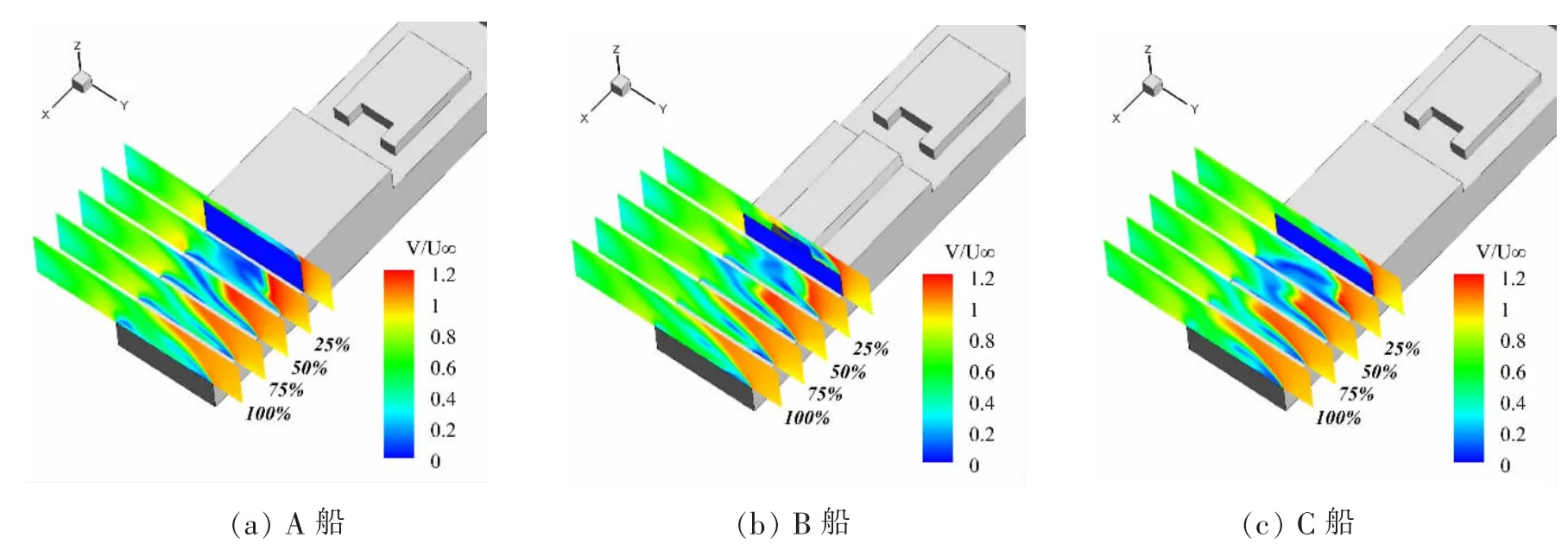
图7 右舷45°风向角下横截面合速度梯度云图Fig.7 Contours of velocity magnitude for the Green 45° case

图7给出了右舷45°风向角下横截面x/l=0，25%，50%，75%，100%处的合速度梯度云图。可以看到，在甲板的右侧出现了y 方向的“回流区”，A 船速度梯度的变化程度明显大于B 船，特别是在近机库区域处（x/l=25%与x/l=50%），而相同位置处C 船速度梯度的变化程度要小于A 船。从由高到低的速度梯度变化中可以得到机库上方边界产生的剪切层位置，同位置处速度梯度的大幅变化会对直升机安全着舰产生一定的影响。

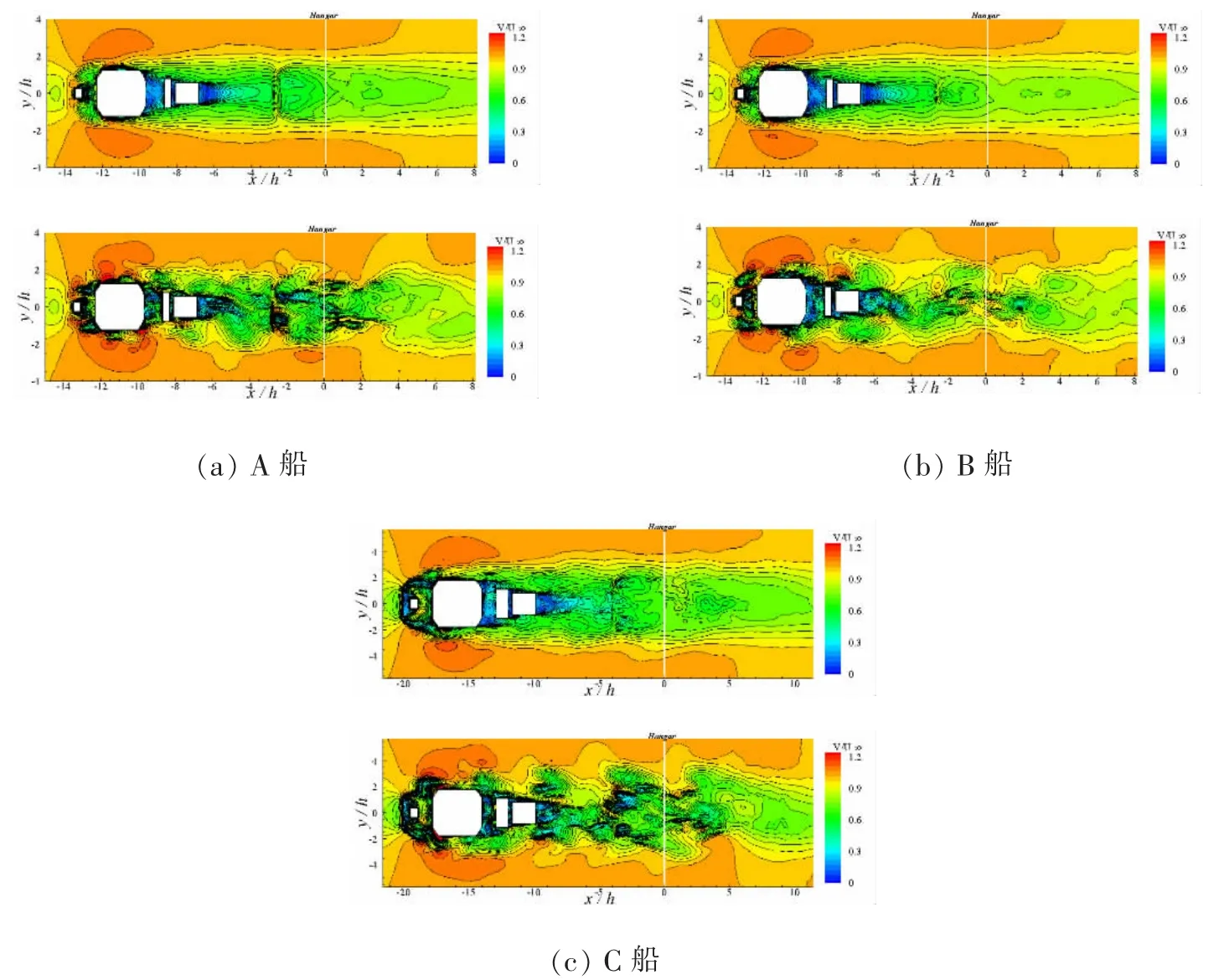
图8 0°风向角下俯视截面z/h=1.15 处合速度梯度云图（上：时均结果，下：瞬时结果）Fig.8 Contours of mean (top) and instantaneous (bottom) velocity magnitude for a headwind,plotted at z/h=1.15 above the deck

图8 与图9 分别为0°与右舷45°风向角下俯视截面z/h=1.15 处合速度的梯度云图。由时均结果可以看出：0°风向角下时均流场结构较为整齐划一，涡结构简单，流动会在建筑的边缘产生分离，导致了自由剪切层；B 船机库两侧较低高度的建筑外形减弱了后方艉流场的速度分离，与A 船相比速度梯度变化较为平缓；45°风向角下，A 船艉部右舷处的速度梯度变化程度明显大于B 船，且影响范围更广。由瞬时结果可以看出：0°风向角下合速度在背风处以及艉部飞行甲板位置处尾迹的不对称性表明了船体的几何建筑构型会出现相干的涡脱落特性。0°与45°风向角下，A 船与C 船飞行甲板上空的流动均较为紊乱，且涡区的覆盖范围更广，而该位置一般为直升机在艉部飞行甲板上方高空盘旋的高度，说明等高机库的外形使得艉流场具有相对紊乱的湍流结构，会对直升机在飞行甲板上方安全盘旋造成不利的影响。

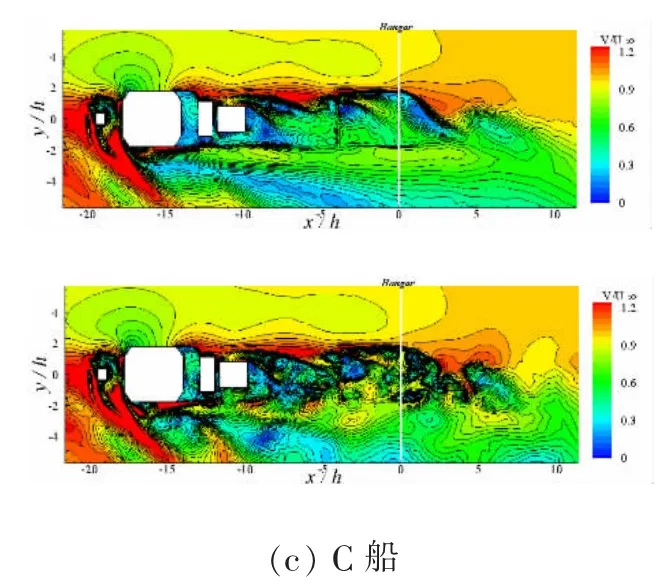
图9 右舷45°风向角下俯视截面z/h=1.15处合速度梯度云图（上：时均结果，下：瞬时结果）Fig.9 Contours of mean (top) and instantaneous (bottom) velocity magnitude for Green 45° case,plotted at z/h=1.15 above the deck

图10 与图11 分别为0°与右舷45°风向角下艉部飞行甲板上方中心直线的下洗速度分布曲线，该直线的位置选择基于直升机在甲板上空悬停时的位置。由结果可见，0°风向角下，A 船最大下洗速度为-0.18U∞，B 船为-0.15U∞，C 船为-0.14U∞，最大下洗速度的位置均约与机库同高。45°风向角时下洗速度有更为明显的梯度变化，约在0.36 倍机库高度处达到极值，A 船最大下洗速度为-0.20U∞，而B 船为-0.15U∞，C 船为-0.12U∞。由此可见，在不同风向角下B 船的最大下洗速度均小于A 船，且具有较低的机库高度的C 船回流区关键区域处的下洗速度明显减弱。

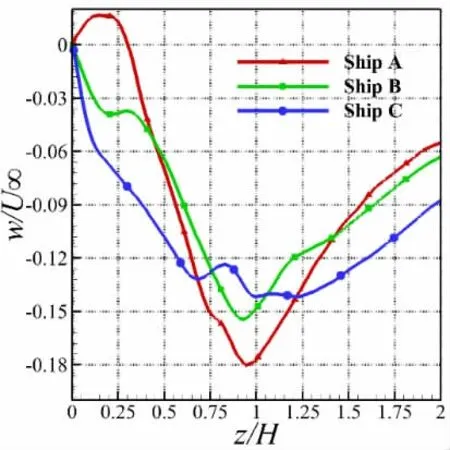
图10 0°风向角下甲板上方中心直线下洗速度分布曲线Fig.10 The downwash velocity component of the flight deck center for a headwind case

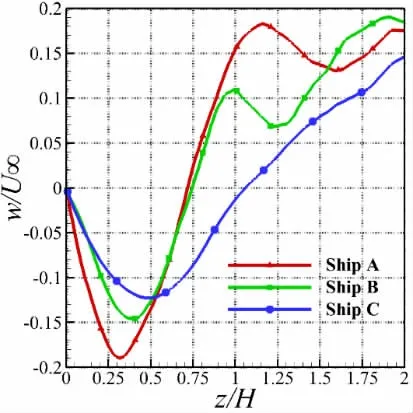
图11 45°风向角下甲板上方中心直线下洗速度分布曲线Fig.11 The downwash velocity component of the f light deck center for Green 45° case

0°与右舷45°风向角下监测点的瞬时速度时域特性如图12 与图13所示，监测点位于飞行甲板正后方（x/l=0.8，y/b=0，z/H=0.6），该位置约为直升机进舰的途经点。可以看出，瞬时速度分量随着时间发生周期性的脉动，表明了流动的非定常特性。0°风向角下，A 船垂向速度最大振幅达到了-0.4U∞～+0.35U∞，B 船为-0.25U∞～+0.2U∞，C 船为-0.05U∞～+0.1U∞，A 船速度震荡剧烈且幅值要远远大于B 船与C 船，且约为B 船的2 倍、C 船的4 倍；相同的趋势也存在于45°风向角下，此时A 船垂向速度的最大振幅达到了-0.6U∞～+0.8U∞，B 船为-0.05U∞～+0.6U∞，C 船为-0.05U∞～+0.5U∞。因此，A 船甲板后方的艉流场速度变化极快，会对直升机进舰的操控性带来严重的影响。

图14 为0°风向角下某瞬时时刻流场的涡量等值面图。涡量的判别依据为λ2准则，λ2为S2+ Ω2的2阶特征值，其中S 为应变率幅值，是速度梯度的对称张量；Ω 为涡量幅值，是速度梯度的反对称张量。从图中可以明显地看出，因舰艏上层建筑而产生的涡结构强度随着气流向艉部流动而逐渐减小，但是遇到艉部机库后涡结构强度又会加强。A 船与C 船整体的涡结构较为相似，而C 船在甲板处的涡结构强度有所减弱。相比拥有与A 船同高机库外形的B 船，B 船因其两侧较低的机库高度使其在甲板处涡结构加强的程度也有所减弱。

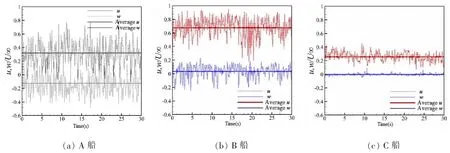
图12 0°风向角下监测点瞬时速度时域特性Fig.12 Time domain characteristics of spectra point for a headwind case

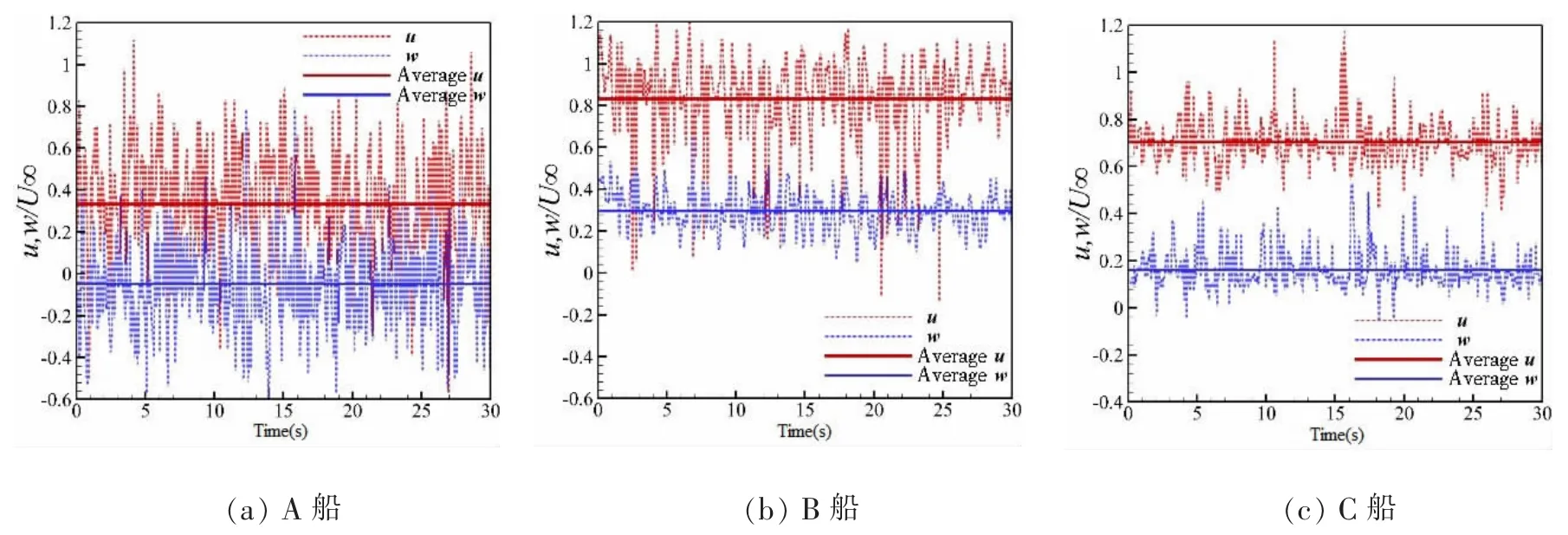
图13 45°风向角下监测点瞬时速度时域特性Fig.13 Time domain characteristics of spectra point for Green 45° case

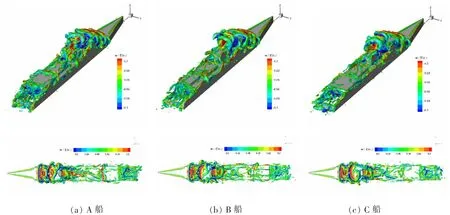
图14 0°风向角下某瞬时时刻流场涡结构Fig.14 Visualization of time-accurate vortex in the airwake (flooded by the magnitude of downwash flow)

4 艉流场回流区范围经验公式探究

Schulman[21]总结并推导了0°风向角下二维后台阶问题中回流区范围的经验公式。后台阶的建筑外形会影响流场回流区的整体结构，建筑外形包括其高度（H），迎风宽度（W）以及气流流经台面的长度（L）。Wilson[22]给出了评价后台阶的长度尺度R 为

式中：BS为较小的迎风高度H，BL为较大的迎风宽度W。

当L＞0.9R 时，流动会在建筑边缘分离后形成自由剪切层，随着流动的发展会在某一位置与后方壁面发生再附，此时回流区的最大高度为HR=H。Fackrell[23]给出了再附点与建筑背风面之间的距离，即回流区纵向范围LR为

用机库高度H 对其进行无量纲化，得LR，H为

由A 船与C 船的机库外形尺寸：

HA=6.5 m，HC=4.5 m，WA=WC=16 m，LA=LC=18 m

可得A 船与C 船的长度尺度RA=8.76 m 和RC=6.88 m，由

LA=18 m＞0.9RA=7.88 m，LC=18 m＞0.9Rc=6.19 m

可知当气流流经A 船与C 船的机库后会与甲板产生再附，其位置为

这与前文所述结论完全吻合。

Schulman[21]给出了二维后台阶问题中回流区垂向范围变化公式：

对于舰船艉流场回流区问题，由公式（3）可以确定不同机库外形的长度尺度，即机库外形的几何因子R。本文根据舰船特殊的建筑构型与公式（5），并对非定常数值仿真计算结果进行拟合，得到了确定等高机库艉部不同横向位置处回流区纵向长度的经验公式LR* 和不同纵向位置处回流区垂向高度的经验公式zH：

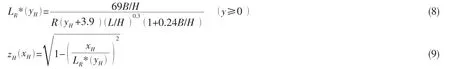
式中：下标H 是用机库高度无量纲化的值。对于公式（8），当y＜0 时取其绝对值。

图15 A 船经验公式验证Fig.15 Verification of empirical equation for ship A

通过经验公式LR*和zH可以对等高机库外形的艉流场回流区范围进行预估。图15 与图16 分别是对A 船与C 船艉流场回流区范围经验公式的验证，由图可以看出本文所推导的经验公式能够准确预测回流区的范围。

图16 C 船经验公式验证Fig.16 Verification of empirical equation for ship C

5 结论

本文采用基于SA 湍流模型的DES 方法对舰船艉流场进行了非定常数值模拟，详细分析了0°与右舷45°风向角下不同机库外形尺寸对艉部流场的影响，得到的主要结论如下：

（1）虽然具有等高机库外形的A 船与两侧具有较低机库高度外形的B 船在艉部产生的回流区范围大体一致，但是和B 船相比，A 船更不利于直升机在艉部飞行甲板上方安全起降与悬停，具体表现为：A 船艉流场速度梯度变化程度大，飞行甲板上空流动更为紊乱，涡区的覆盖范围更广且机库后方涡结构强度更强，飞行甲板中心直线上的下洗速度比B 船分别大3%（0°风向角）与5%（右舷45°风向角），飞行甲板艉部上方的垂向速度振幅过大，相当于B 船的2 倍；

（2）降低机库高度会使回流区位置相对前移，因此通过合理设计机库高度可以使回流区有效避开直升机的着舰域。较低的机库高度使得艉部速度梯度变化趋于平缓，且大幅度降低了关键位置处的下洗速度和艉部涡结构的强度，同时提升了直升机进舰的稳定性；

（3）通过经验公式可以快速预测艉流场回流区的范围与位置，为直升机着舰提供相应的参考信息，增加其着舰的安全性。