基于不同参数模型的安全计算机共因失效分数计算及比较分析
2019-06-04王巨汉
高 莺,王巨汉,张 琦,唐 涛,曹 源
(1.中国铁道科学研究院 研究生部,北京 100081;2.中国铁道科学研究院集团有限公司 国家铁路智能运输系统工程技术研究中心,北京 100081;3.北京交通大学 电子信息工程学院,北京 100044;4.中国铁道科学研究院集团有限公司 通信信号研究所,北京 100081;5.北京交通大学 轨道交通运行控制系统国家工程研究中心,北京 100044)
列车运行控制系统作为保障铁路运营安全的高安全苛求系统,其安全计算机在组成上多采用冗余配置。共同原因失效(Common Cause Failure, CCF)是冗余结构系统不可回避的问题,由于共同原因故障导致元器件发生关联失效,既降低了系统的可靠性,又为系统失效(特别是系统危险侧失效)埋下隐患,已成为威胁铁路运行安全的重要因素。因此,列车运行控制系统在系统设计时,应充分考虑安全计算机共同原因失效的可能性,在系统平均危险侧失效概率(PPFH)计算中也应关注共因失效分数的计算。
现有研究中计算共因失效分数的应用不少,但计算方法较统一,多使用Beta(以下简称“β”)参数模型,然而β参数模型对共同原因失效的原因划分单一,不适用于高阶共因失效分数计算。文献[1]研究了外部因素导致的概率性共同原因失效及其可靠性计算,但计算内容未涉及危险侧失效概率。文献[2]对β参数模型做了改进,应用于石油工业的共因失效分数计算,但文章中没有分析改进的模型较原模型在共因失效分数计算中有何提升。文献[3]使用Alpha(以下简称“α”)参数模型计算辅助给水系统的共因失效分数,但文章没有给出α参数模型与其他参数模型的对比。文献[4—6]介绍了用于共因失效分数计算的多希腊字母模型,该模型实质上是现有β参数模型的细化,在高阶共因失效分数计算时仍存在推广困难。国内相关文献[7—9]介绍了包括α参数模型在内的多种计算模型,但文献仅限于介绍模型原理,没有实际应用案例分析。
本文在已有文献研究的基础上,通过标准IEC61508中推荐的β参数模型,计算获得计算机联锁系统的共因失效分数,分析该模型在计算高阶共因失效分数上存在的不足;然后提出基于历史故障数据的α参数模型的共因失效分数计算方法,并建立2种参数模型的等价关系。分别对2乘2取2冗余结构和3取2冗余结构,采用2种参数模型计算PPFH,验证α参数模型可以获得更加精确的共因失效分数和PPFH。
1 安全计算机PPFH计算过程
计算机联锁系统是列车运行控制系统的重要组成部分,图1为该系统安全计算机的2种典型冗余结构,分别是2乘2取2结构和3取2结构。计算机联锁设备中驱采计算机的采集部分、联锁计算机的逻辑部分和驱采计算机的驱动部分共同承担安全功能,3个子系统本身也均为冗余结构。
IEC61508-6附录中提供了不同冗余结构的PPFH计算方法[10]。在列车运行控制系统中,冗余结构较为常见的表决组结构包括1oo2,2oo2和2oo3。3种表决组各自的PPFH计算公式为
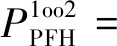
(1-β)λDUtCE+βλDU
(1)
(2)

(1-β)λDUtCE+βλDU
(3)
其中,
λDU=λD(1-FDC)
λDD=λDFDC
式中:β和βD分别为无法诊断和可诊断测试识别的共因失效分数;λDU和λDD分别为未诊断和可诊断测试识别的危险侧失效概率;λD单通道危险侧失效概率;T1为检验测试时间间隔;TMTTR为平均恢复时间;FDC为诊断覆盖率。
IEC61508中,将安全计算机划分为输入、逻辑计算和输出3个子系统,安全计算机的PPFH等于各子系统PPFH之和,即
(4)

PPFH计算中,首先求得每个2oo2结构的危险侧失效概率,然后以该失效概率作为1oo2或2oo3结构每个通道的危险侧失效概率,计算2乘2取2结构或3取2结构的PPFH。

图1 系统安全计算机的2种典型冗余结构框图
由式(1)—式(3)可知,计算PPFH的公式中重要参数包括β,βD,λDU,λDD,λD,T1,TMTTR和FDC,其中共因失效分数β和βD仅能通过计算得出,其他参数可通过现场试验数据或用户要求获得,因此,本文着重研究共因失效分数β和βD的计算方法以及其对PPFH计算结果影响的分析。
2 采用β参数模型计算共因失效分数
β参数模型由Fleming提出,该模型使用单一参数β定义部件由共同原因导致的失效占总失效的比例。β参数模型是当前铁路领域计算PPFH最常用到的共因失效分数计算模型,该模型通过判断系统是否采取防御共同原因失效的措施来确定共因失效分数。IEC61508-6附录D中提供了防御共同原因失效的措施列表(包括分离隔离、多样性与冗余、复杂性设计应用等8个大类[10]),并定义了每项措施的贡献度分值X和Y。
以计算机联锁系统为分析对象,根据其逻辑计算和输入/输出3个子系统的设计要求,对照IEC61508-6中TableD.1的检查项进行逐项打分,将分值相加得到每个子系统的X和Y值,进而根据IEC61508-6中TableD.2~3的Z值评判表确定Z值。所得的X,Y,Z值见表1。

表1 各子系统X,Y,Z值
参数S和SD的计算公式为
S=X+Y
(5)
SD=X(Z+1)+Y
(6)
将表1中的数据代入式(5)和式(6),计算得到逻辑计算子系统的S=82,SD=139,输入/输出子系统的S=73,SD=118.75。
IEC61508-6中给出的S与β(SD与βD)的对应关系见表2。查表2可得:逻辑计算子系统β=1%,βD=0.5%;输入/输出子系统β=2%,βD=2%。

表2 β(βD)的取值
3 采用α参数模型计算共因失效分数
由上述计算过程可知,β参数模型把随机失效单纯分为2类,即独立失效(有且只有1个通道发生失效),共同原因失效(所有通道失效,且失效原因相同)。对于3阶冗余结构的系统(如3取2结构),β参数模型认为2通道失效的概率为零,系统只存在单通道失效以及3通道同时失效2种情况。因此在计算3重及3重冗余以上的共因失效分数时,β参数模型的计算结果存在偏差。同时,该模型采用查表分析法,计算结果对应取值的区间大且分类简单(详见表2),也不利于获得精确的共因失效分数。
列车运行控制系统的冗余结构通常为2通道和3通道,为了计算更加精确的PPFH,本文引入在核电领域使用的α参数模型。首先通过模型的构建原理证明其更适合于3阶及以上冗余结构的共因失效分数计算,进而针对铁路领域安全计算机缺乏共同原因失效历史统计数据的问题,结合美国核管理委员会(United States Nuclear Regulatory Commission, U.S.NRC)的先验参数,获得列车运行控制系统安全计算机不同冗余结构下的共因失效分数。
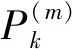
(7)
其中,
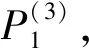
P(A)=P(CA)+P(CAB)+P(CAC)+P(CABC)
(8)
其中,
对于3取2结构的安全计算机,如果系统中2个或2个以上通道失效时系统不再安全,那么,在计算该系统由共因失效导致的危险侧失效概率时,PPFH应包含2通道共同原因失效和3通道共同原因失效2类,即

(9)
(10)
同理,可得2乘2取2结构的俺全计算机,式(1)中β与α因子的关系为
β=α2
(11)
在应用α参数模型计算PPFH时,需确定变量αk,k=1,2,…,m。由于目前我国列车运行控制系统缺少针对安全计算机中共同原因失效数据的统计,在确定α参数模型的变量αk时,本文参考了美国核管理委员会在核能发电领域发布的年度共同原因失效统计结果,并将其作为变量αk计算的先验数据进行修正[12-13]。
首先αk的先验数据服从β分布,即
(12)
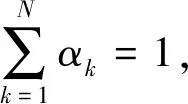
(13)
式中:ak指系统发生k个通道共同原因失效的次数;bk指除了发生k个通道共同原因失效外,其他类型失效发生的次数。

(k=1,2,…,m)
(14)
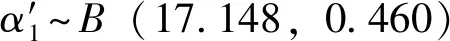
将表3、表4中αk值分别代入式(10)、式(11),计算得到3取2结构和2乘2取2结构安全计算机的共因失效分数β,结合IEC61508-6中定义的β=2βD,进而通过式(1)—式(3)计算获得采用α参数模型的PPFH。
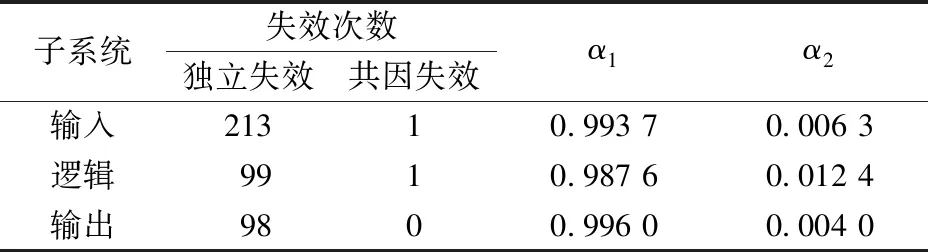
表3 2乘2取2冗余结构αk值
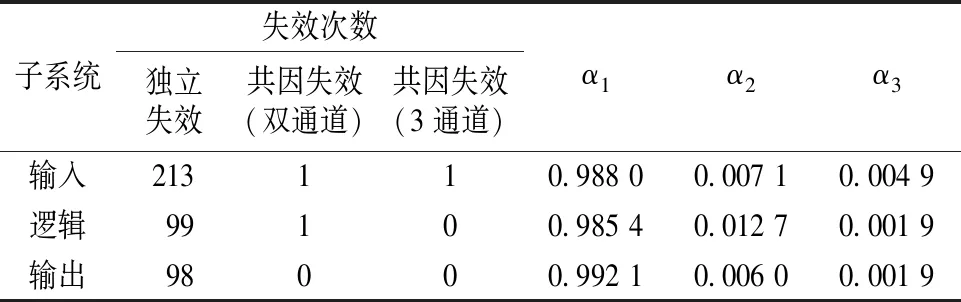
表4 3取2冗余结构αk值
4 计算结果及对比分析
根据既有计算机联锁系统的可靠性数据,取输入子系统的λD=1.00×10-7次·h-1,FDC=90%;逻辑计算子系统的λD=3.80×10-7次·h-1,FDC=99%;输出子系统的λD=5.00×10-7次·h-1,FDC=90%;3个子系统的T1=8 760 h;TMTTR=1 h。
4.1 2乘2取2结构安全计算机的危险侧失效概率计算
针对2乘2取2结构,分别采用β参数模型和α参数模型,计算得到共因失效分数β和βD,然后代入式(1)和式(4),可分别计算得到由独立失效(独立故障原因)或由共因失效(共因故障原因)导致的危险侧失效概率,计算结果见表5和表6。
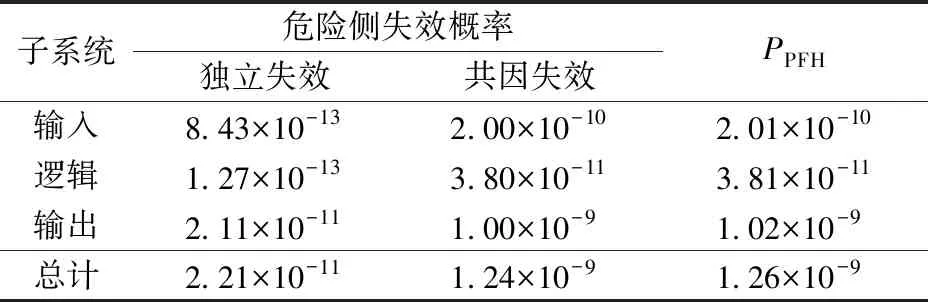
表5 使用β参数模型的计算结果(2乘2取2结构)

表6 使用α参数模型的计算结果(2乘2取2结构)
图2显示了2乘2取2结构下,分别采用β参数模型和α参数模型时3个子系统的PPFH计算结果,可以明显看出,两者差别较大。图3显示了2种参数模型下共因失效导致的危险侧失效概率。将图3与图2对比可知:共因失效导致的危险侧失效概率约等于PPFH的计算结果,说明共因失效分数是决定PPFH计算结果的重要参数。

图2 2种参数模型计算PPFH对比
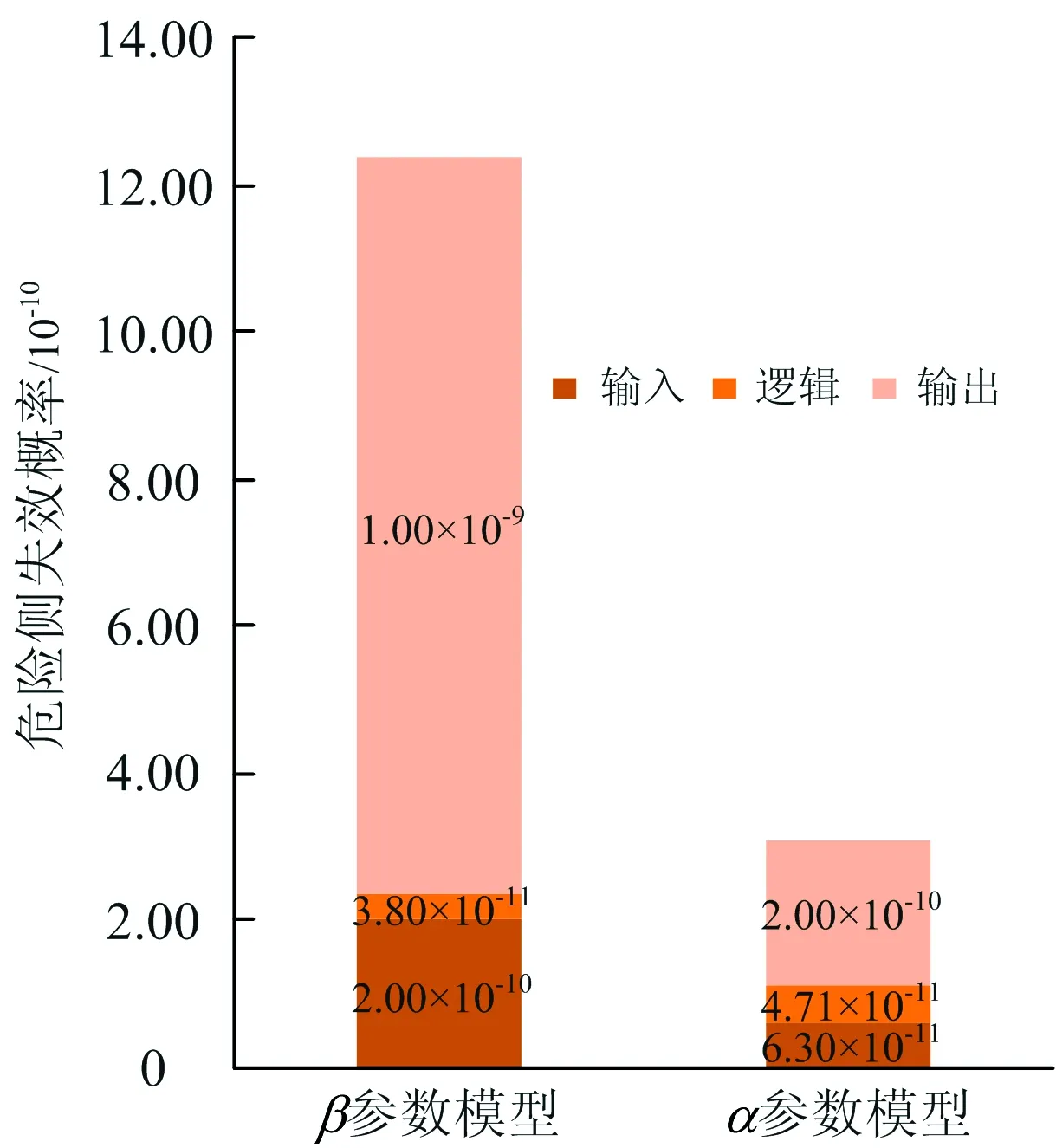
图3 共因故障导致的危险侧失效概率对比
4.2 3取2结构安全计算机的危险侧失效概率计算
针对3取2结构,分别采用β参数模型和α参数模型,计算得到共因失效分数β和βD,然后代入式(3)和式(4),可分别计算得到由独立失效(独立故障原因)或由共因失效(共因故障原因)导致的危险侧失效概率,计算结果见表7和表8。
由表5—表8可知:基于当前历史数据的α参数模型较β参数模型得到的PPFH更小,其原因在于当前用于计算共因失效分数的故障数据有限,当随着设备或相似设备的共同原因失效数据累积,对应的αk被不断修正,该模型计算的PPFH与实际情况较接近。

表7 使用β参数模型的计算结果(3取2结构)

表8 使用α参数模型的计算结果(3取2结构)
4.3 采用2种参数模型时2种冗余结构危险侧失效概率的对比
结合4.1节和4.2节的计算结果,针对不同冗余结构,采用2种参数模型分别计算由独立失效(独立故障原因)或由共因失效(共因故障原因)导致的危险侧失效概率,如图4和图5所示。
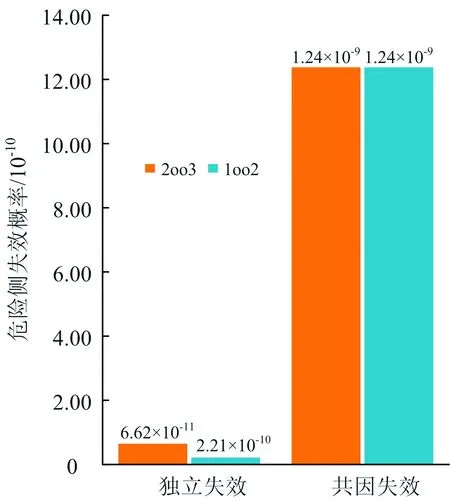
图4 采用β参数模型时不同冗余结构PPFH组成
对比图4和图5可知:基于2乘2取2结构和3取2结构计算得到的PPFH中,共同原因失效对其贡献度大于独立失效,且α参数模型计算得3取2结构的共同原因危险侧失效概率高于2乘2取2结构,与实际情况相符;α参数模型能够区分不同冗余结构下独立失效和共同原因失效导致的危险侧失效概率,但β参数模型中无法区分共同原因失效导致的危险侧失效概率,这也是该模型不适用于高阶共因失效分数计算的原因之一。

图5 采用α参数模型时不同冗余结构PPFH组成
5 结 语
以计算机联锁设备为安全计算机研究对象,分析了经典β参数模型计算共因失效分数的不足,提出引用核能领域的α参数模型计算共因失效分数,同时采用先验分布解决了列控系统安全计算机缺乏共同原因失效统计数据的问题。对计算机联锁系统安全计算机的2种常见冗余结构,分别采用这2种参数模型计算其共因失效分数,从而计算PPFH和共同原因失效导致的危险侧失效概率。结果表明:共因失效导致的危险侧失效概率是PPFH的主要组成部分,α参数模型能够量化计算3重及以上冗余结构的共因失效分数,并获得更符合实际输出的PPFH计算结果。同时,当共因失效数据不断完善时,α参数模型可以通过修正后验参数获得更准确的共因失效分数,为验证安全计算机安全完整性等级提供有利帮助。
