基于数据替补修正的高速铁路日常客运量VMD-GA-BP预测方法
2019-06-04杨星琪胡心磊徐光明武润发
史 峰,杨星琪,胡心磊,徐光明,武润发
(中南大学 交通运输工程学院,湖南 长沙 410075)
高速铁路客运量预测问题分为年度预测,月度(季度)预测和日客运量预测,主要采用自回归积分滑动平均模型(ARIMA)、灰色预测(GM)、人工神经网络(ANN)、支持向量机回归(SVR)等方法拟合现有数据,用趋势外推的思想对运量进行预测。由于节假日客运量具有不同于非节假日的波动规律,因此日客运量预测通常分为日常客运量预测和节假日客运量预测,本文所指的日常客运量是指以“日”为单位的非节假日高速铁路客运量。高速铁路日常客运量预测在票额分配、增开临时列车和营销策略制定方面具有重要意义。
针对客运量预测问题有很多研究成果,在这些研究成果中,针对具体的研究问题建立不同的预测模型,其预测精度也有差异。汪健雄等[1]采用双层特征分析方法提取铁路旅客发送量的时间特征作为模型的输入变量,建立双层BP神经网络模型,根据Gram-Schmidt正交化定理对双层BP神经网络进行改进,预测精度较BP神经网络模型更高且达到期望均方差所需的步长更短。王卓等[2]采用加入动量因子、自适应学习速率和附加动量的方法改进BP神经网络,对铁路客运量时间序列进行预测,结果表明最大相对误差为5.4%。王艳辉等[3]以春运期间的铁路客运量为依据,将客运量的空间属性和时间属性有机地结合起来,建立BP神经网络预测模型,结果表明平均相对误差为3.36%。Jia等[4]建立综合GM和自回归滑动平均模型(ARMA)的组合预测模型,并利用轨道交通客流量对该模型进行验证,结果表明平均相对误差为5.8%。姚恩建等[5]提出基于改进K近邻非参数回归的城市轨道交通新站开通初期实时进出站客流量预测方法,结果表明平均相对误差低于17%。现有的客运量预测方法主要分为以ARIMA和GM为代表的参数法、以ANN和SVR为代表的非参数法以及融合多种方法的组合模型,其中组合预测模型由于融合多种方法的优势,往往精度较高[6]。
但现有的预测方法大多未考虑节假日因素对日常客运量预测工作的干扰,且未有效挖掘客运量本身蕴含的周期性规律,因此,本文针对高速铁路日常客运量预测问题,采用数据替补修正法消除节假日因素的影响,提出1种融合变分模态分解(VMD)、遗传算法(GA)和BP神经网络的日常客运量VMD-GA-BP组合预测方法。
1 日常客运量预测问题分析
尽管日常客运量与节假日客运量分开预测,但节假日客运量及其分布直接影响到日常客运量的分布规律,因此在日常客运量预测时应消除节假日客运量的影响。
1.1 节假日客运量特征
我国放假的节日包括元旦节、清明节、劳动节、端午节、中秋节、国庆节和春节,共7个。前5个节日放假1天,后2个节日放假3天,由于周末调休,前5个节日的连续放假时间一般为3天,后2个节日的连续放假时间为7天,通常对节假日的理解是节日相关的连续放假时间。另外,除了节假日客运量比日常客运量有所增加以外,节假日前后的客运量也会有所增加。本文将节假日及其前后受到其影响导致客运量异常波动的总延续日期称为节假日延续期,不同节假日延续期和客运量增幅存在差异。
以宁安高速铁路南京南站至安庆站2016年8月至2017年7月的客运量为例,节假日延续期内客运量分布特征如图1所示。图中:“前3”表示节假日前第3天;“节1”表示节假日第1天;“后3”表示节假日后第3天;其余类推。由图1可以得出如下结论。
(1)5个3天假期延续期内的客运量都具有“双峰”分布特征,即节假日前3天客运量开始增长,节假日前1天达到峰值;节假日期间客运量开始略微回落并保持在较高水平,节假日最后1天客运量再次达到峰值(或回落速度降低,见端午假期);节假日过后客运量波动下滑,到节假日后第3天回归到日常客运量水平。
(2)国庆节的客运量出现了“3个高峰”,第1个高峰和第3个高峰分别出现在节假日前第1天和节假日最后1天,这与3天假期有相似之处,第2个高峰出现在节假日第4天。
(3)春节虽然也是7天假期,但由于春节假期与春运时间是连在一起的,春运时间是指春节向前延续15天、往后延续25天,共计40天,因此春节7天假期延续期的客运量从春运第1天开始增长并在春节前第9天达到高峰,之后逐步回落并在春节当天降到最低谷,此后出现反弹,但在春运后期并没有显著表现出较高的客运量,到春运最后1天回归到日常客运量水平。

图1 不同节假日延续期内客运量分布特征
1.2 节假日延续期识别
对于不同线路不同O-D,因为节假日延续期和客运量增幅存在差异,所以有必要识别节假日延续期,消除节假日对日常客运量预测精度的影响。本文根据日客运量平均波动幅度变化率进行识别。
记第t天的客运量为X(t),第t-1天与第t天日客运量的变化率为βt,定义第t-1天与第t天的日客运量波动幅度变化率为日客运量之差的绝对值与日客运量均值的商,即
(1)
对于为期N天的指定期间,定义日客运量平均波动幅度变化率为
(2)
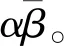
判定第t天为超常波动日的法则为:当且仅当式(3)成立。只要超常波动判定阈值设定恰当,便可非常简便地发现超常波动日。
(3)
由式(3)可以确定节假日之前的客运量起始增长日、节假日之后的客运量终止回落日,自起始增长日至终止回落日即为节假日延续期。
1.3 节假日客运量替补修正
节假日客运量替补修正法是消除节假日对日常客运量预测精度影响的方法,是将节假日延续期内的客运量用日常客运量的预测值替换,其算法流程如图2所示。首先基于超常波动判定阈值确定节假日延续期,节假日延续期内的客运量为将被替换的数据,用0表示;其次以被替换数据之前的数据序列为训练集,采用VMD-GA-BP组合预测方法对节假日延续期内的客运量进行预测,将预测值作为替换数据进行数据替换;重复上述过程,直到所有节假日延续期内的数据均被预测值替换,最终得到消除节假日因素影响的修正客运量。其中所采用的VMD-GA-BP组合预测方法将在下文进行介绍。

图2 节假日客运量替补修正法流程
2 VMD-GA-BP组合预测方法的构建
2.1 GA-BP预测方法
BP神经网络具有优良的多维函数映射能力,其拓扑结构包括输入层、隐含层和输出层。考虑到BP神经网络容易陷入局部最优,采用遗传算法GA对BP神经网络的初始权值和阈值进行优化,构建GA-BP预测方法。
GA-BP预测方法的原理为:GA包括种群初始化、适应度函数、选择操作、交叉操作和变异操作。种群是由多个个体组成,每个个体是由BP神经网络初始权值和阈值构成的实数串;采用预测输出和期望输出的误差绝对值作为适应度函数,判定每个个体的优劣;将较好的个体以更大概率遗传给下一代,同时进行个体间交叉、个体变异等操作,即生成新一代种群和个体;在满足GA终止条件后将最优个体代表的初始权值和阈值赋给BP神经网络。GA-BP预测方法流程如图3所示[7]。

图3 GA-BP预测方法流程
2.2 变分模态分解方法
高速铁路客运量的多少是多种因素共同作用的结果,采用时频分析方法对客运量数据序列进行分解,能够将影响客运量的多种因素剥离出来,得到不同频率的分量,对这种具有一定周期规律的分量进行预测,预测精度往往更高。目前应用在交通领域的时频分析方法主要有小波变换(WA)[8]和经验模态分解(EMD)[9-10],但这2种方法分别存在难以构造合适小波基和模态混叠的不足。
针对上述存在的问题,引入目前时频分析领域较新的研究成果变分模态分解VMD[11-12]对数据序列进行模态分解,VMD方法的原理如下。
VMD将特征模态函数uk(t)[13]定义为1个调幅调频信号,即
uk(t)=Ak(t)cos[φk(t)]
(4)

为了评估模态的带宽,需经过如下步骤:
(1)对每个模态函数uk通过希尔伯特变换计算相应的解析信号,获得单边频谱;
(2)对每个模态函数uk通过与指数混合解调到各自估计的中心频率,将模态的频谱转换到基带;
(3)通过解调信号的高斯平滑,即梯度的L2范数,估计每个模态的带宽。
所得约束变分模型为
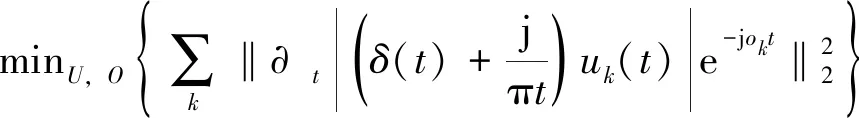
(5)
s.t.
式中:X为客运量时间序列;U={u1,u2, …,uk}为所有模态的集合;O={o1,o2, …,ok}为所有模态的中心频率集合;k为预设的分解尺度。
在求约束变分模型的最优解中,为了使变分问题不受约束,引入惩罚因子M和拉格朗日乘子λ构造如下形式的增广Lagrange函数:
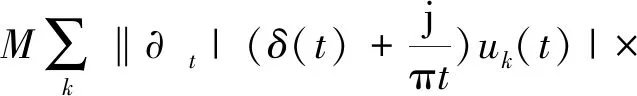
(6)

(7)
(8)
(9)

2.3 VMD-GA-BP组合预测方法
将VMD与GA-BP进行组合,提出VMD-GA-BP组合预测方法,即通过VMD将数据序列分解成具有不同中心频率的k个模态分量u1~uk,采用经GA优化初始权值和阈值的BP神经网络对不同频率的模态分量进行预测,重构各模态分量的预测值F1~Fk,使日常客运量的预测精度更加准确。VMD-GA-BP组合预测方法流程如图4所示。

图4 VMD-GA-BP组合预测方法流程
3 实例分析
宁安高速铁路于2015年12月开通运营,全长257 km,共设南京南、江宁西、马鞍山东、当涂东、芜湖、弋江、繁昌西、铜陵、池州和安庆10个站。以该线路2016年8月至2017年7月客运量进行算例验证,取前11个章的数据为训练集,第12个月的数据为测试集。超常波动判定阈值系数取最小阈值系数与最大阈值系数的平均值。
3.1 VMD模态分解结果
取VMD的分解尺度k等于EMD分解的特征模态分量个数m(EMD为自适应分解,m的大小由数据序列本身特征决定)。采用VMD对全部数据进行分解,分解得到8个模态分量u1~u8,按照从低频至高频顺序排列如图5所示。从图中可以看出,VMD方法分解得到的低频分量能很好地体现客运量整体趋势,中频分量能较好地体现不同的周期特性,而高频分量则较难看出规律性。
进一步计算8个模态分量的中心频率,以其倒数(即周期)分析各模态分量反映的客运量波动规律。u1体现数据序列的整体趋势;u2的波动周期为34.26天,这近似反映了1个月的波动规律;u3的波动周期为14.56天,反映了14天的波动规律;u4的波动周期为7.19天,反映了1周7天的波动规律;u5~u8无法准确描述客运量波动规律产生的原因,但它们仍然储存着数据序列的信息,不能轻易去除。
采用VMD-GA-BP预测方法对所有节假日延续期内的客运量进行替补修正,得到消除节假日因素影响的修正客运量。然后采用VMD对修正客运量进行分解,分解得到7个模态分量u1~u7。结果按低频至高频排列如图6所示,可以看出修正后的客运量自适应分解层数变少,复杂性降低。同样,进一步计算7个模态分量的中心频率,以其倒数(即周期)分析各模态分量反映的客运量波动规律可知,u1体现数据序列的整体趋势;u2的波动周期为18.43天,介于图5中u2和u3的周期之间;u3的波动周期为7.07天,反映了7天的波动规律;u5~u7都无法准确描述客运量波动规律产生的原因,但仍不能轻易去除。

图5 原始数据序列变分模态分解结果

图6 修正数据序列变分模态分解结果
从原始数据序列的周期计算结果可知,u4的波动周期为7.19天;从修正数据序列的周期计算结果可知,u3的波动周期为7.07天,可见修正后的日常客运量在1周7天的波动特征上更加明显,说明通过数据修正,消除了节假日延续期内大客流异常波动对日常客流的影响。
3.2 VMD-GA-BP预测结果
BP神经网络是VMD-GA-BP组合预测模型的核心,除了初始权值和阈值影响BP神经网络的性能,输入变量个数也会对预测误差产生影响。对于BP神经网络模型,如果输入变量过少,无法获取影响客运量的大部分历史信息;如果输入变量过多,则会增加网络训练难度。因此,取输入变量数为7~14个,通过预测误差判断最优的输入变量个数。在确定输入变量个数后,针对不同模态分量个数与隐含层节点数的组合,对修正后的数据序列采用本文方法进行预测,以预测误差确定模态分量个数与隐含层节点数之间的最优组合。不同组合的预测误差对比如图7所示,从图中可以看出预测误差主要位于3个区间,即0~0.01,0.01~0.02,0.02~0.04。

图7 模态分量个数与隐含层节点数的优化组合
采用模态分量个数与隐含层节点数的最优组合,以修正数据序列作为输入数据,采用本文提出的VMD-GA-BP组合预测方法,预测南京南站-安庆站间的客运量,将预测结果与实际值对比如图8(a)所示。同时,选取宁安高速铁路南京南站至芜湖站(即起点站至中间站)、芜湖站至安庆站(即中间站至终点站),采用本文方法进行预测,以验证预测方法的适应性,结果如图8(b)、图8(c)所示。由图8可知:客运量的预测值与实际值基本相同,说明本文方法对高速铁路日常客运量预测问题有较好的预测精度。
3.3 多种方法预测误差对比
仍取南京南站至安庆站间的客运量,针对原始数据和修正数据,分别采用本文提出的VMD-GA-BP预测方法和BP神经网络方法进行预测。同时针对原始数据,采用既有的客运量预测方法进行预测,既有方法主要包括EMD-GA-BP、支持向量机回归(SVR)、EMD-BP、极限学习机(ELM) 、广义回归神经网络(GRNN)、Elman神经网络、GA-BP、灰色预测(GM)和小波神经网络(WNN)。预测误差采用平均相对误差ΔMAPE、绝对误差ΔMAE、均方根误差ΔRMSE这3个指标判定本文方法与既有方法在高速铁路日常客运量预测问题上的适应性。
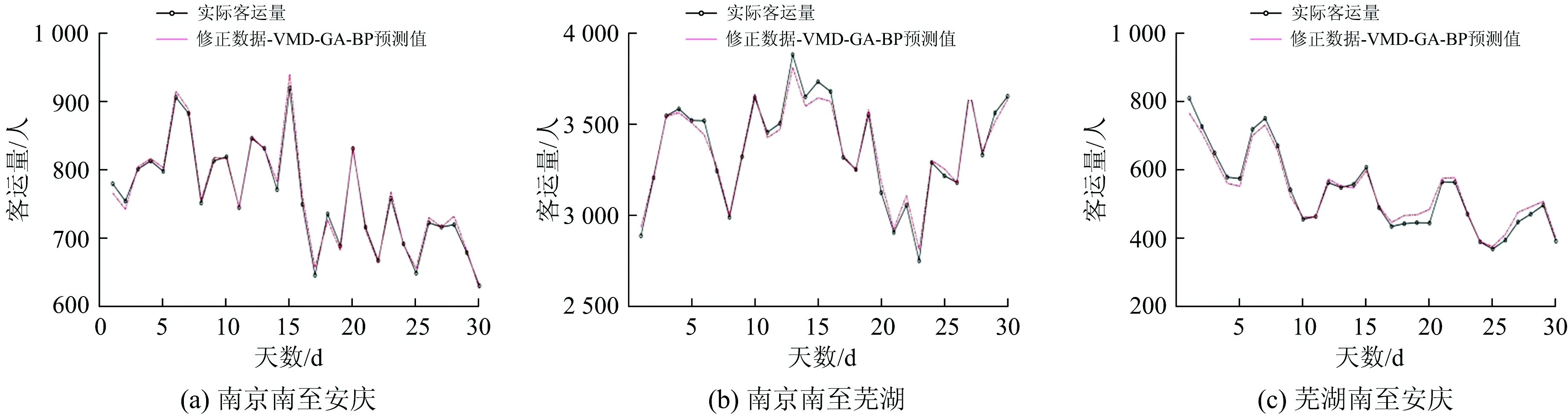
图8 客运量预测值与实际值对比
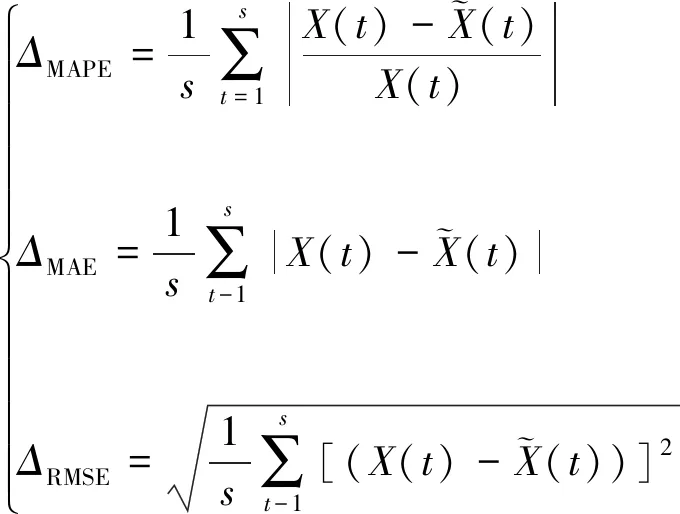
(10)
针对该实例,不同模型的预测误差对比如表1和图9所示。根据表1和图9可得如下结论。从数据修正效果上看:采用VMD-GA-BP进行预测,使用修正数据序列与使用原始数据序列相比,预测误差从0.84%降低到0.80%;采用BP神经网络进行预测,使用修正数据序列与使用原始数据序列相比,预测误差从10.49%降低到8.28%;这验证了本文提出的数据修正方法在减少预测误差和提高预测精度上是有效的。从数据分解方法上看:在都使用原始数据序列的情况下,采用VMD-GA-BP与采用EMD-GA-BP相比,预测误差从5.20%降低到0.84%,这说明采用VMD分解后的模态分量预测效果要好于采用EMD分解。将本文VMD-GA-BP预测方法与其他方法相比,无论采用原始数据还是修正数据,预测误差均降低许多,说明本文方法在高速铁路日常客运量预测问题上具有更好的适应性。
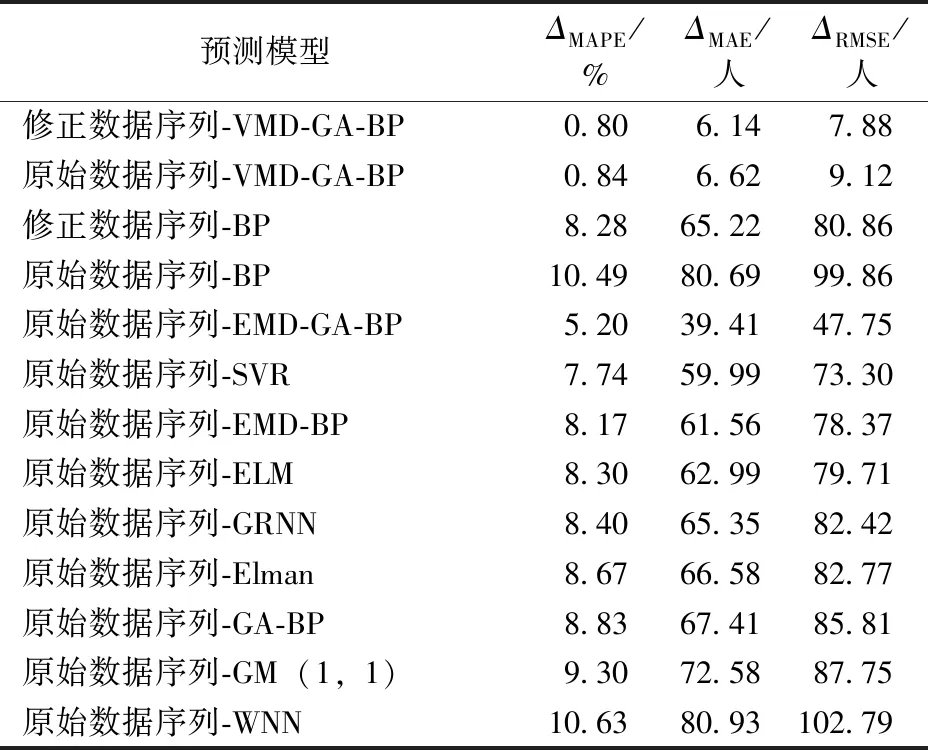
表1 多种模型预测误差对比

图9 部分模型预测误差对比
对修正数据序列和原始数据序列,均采用VMD-GA-BP预测方法进行多步预测,运行10次取其平均值,误差见表2。由表2知:当预测步长为14时,对修正数据序列的预测误差要明显低于对原始数据序列,这说明本文提出的数据替补修正法能够有效提高日常客运量多步预测的精度。

表2 多步预测误差对比
4 结 论
(1)为了提高高速铁路日常客运量预测精度,提出一种消除节假日因素影响的数据替补修正法。即根据日常客运量超常波动判定阈值识别节假日延续期,采用VMD-GA-BP预测方法得到的预测值,用该预测值替换节假延续期内的客运量。本方法既能够消除节假日因素对日常客运量预测精度的影响,又不破坏日常客运量的规律。
(2)将VMD引入GA-BP,提出高速铁路日常客运量VMD-GA-BP预测方法,能够实现对日常客运量波动规律的提取,并通过将客运量分解为高、低频分量,使非平稳数据进行平稳化处理。实例表明,采用VMD-GA-BP预测方法,能够有效降低日常客运量预测误差。该方法具有良好的预测精度和实用性。
