基于SAS NLMIXED的广义线性混合效应模型在发病率数据Meta分析中的应用

2019-06-04郑建清黄碧芬肖丽华

中国循证儿科杂志 2019年2期

郑建清黄碧芬吴敏肖丽华

Meta分析被越来越广泛地用于医学研究，通过汇总来自多个独立研究的资料来评估某种干预的有效性，也可以用于因果关系及率的综合分析。当研究人员所关心的结局变量是二分类变量时，这类数据可以被视为一个2×2的列联表，每个单元格对应于不同组中的事件数和无事件数(例如研究组和对照组中有疾病和无疾病的人数)。然后，可以通过风险差(RD)、相对危险度(RR)或者比值比(OR)等指标来汇总这些研究中收集的信息。临床中，另外一个常用的效应指标为发生率比率(IRR)，又称为发病率密度，是基于每个研究组单独记录的事件计数随时间的变化情况，例如每1 000人年。将这种类型的数据称为发病率数据，也称为发病率密度数据[1]。

目前已经提出了两种方法来进行发病率数据的Meta分析，包括倒方差法和基于固定效应模型的泊松回归模型[2-4]。当数据存在“0事件”(多个研究在研究的1或2个组中具有0事件)时，倒方差法是有问题的，因为当研究包含0事件时，研究特定的效应值log IRR及其方差都无法定义。因此，最终分析的时候会省略含0事件研究。一种被广泛推荐使用的补救措施是应用连续性校正，但这种方法通常仅在只有少数研究包含0事件的情况下使用，否则会产生明显的偏倚。基于固定效应模型的泊松回归模型可以解决暴露时间变化的情况，也可以用于解决数据中存在0事件的问题。另一种选择是通过基于随机效应模型的泊松回归模型来扩展先前的模型，但这种方法很少被用于上述情况。其优点在于，除了潜在地处理0事件和改变暴露时间之外，还可以解决干预效应存在异质性的问题[4]。

本研究的目的是介绍如何利用SAS软件中的NLMIXED过程步实现基于广义线性混合模型的泊松-正态模型(Poisson-Normal Model，PNM)和二项式-正态模型(Binomial-Normal Model，BNM)在稀有发病率数据中的Meta分析技术，尤其是包含0事件的数据。本文采用基于正态-正态模型(Normal -Normal Model，NNM)的方法(包括是否采用连续性校正)作为比较。本文介绍的基于广义线性混合模型的PNM和BNM由Stijnen等人提出，并通过小型模拟试验证实是行之有效的方法[5]。本文提供了各种模型的SAS代码，这些代码简洁明了，使用方便。

1 基于倒方差方法的正态-正态Meta分析模型简介

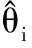
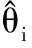
其中假设标准误Si是已知的，而均值θi是待估计的。由于异质性的存在，真实值θi可能因研究而异，而θi也被假设服从正态分布，即：

θi≃N(θ, σi2) (公式2)

参数θ是感兴趣的主要参数，称为整体效应，而σ2描述了不同研究的真实效果的变异。公式1和2被称为NNM。统计学推断基于以下的似然性：

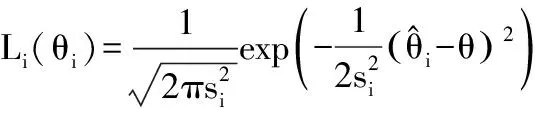
普通最大似然法(Maximum Likelihood，ML)或约束最大似然法(Restricted Maximum Likelihood，REML)均可用于估计参数。

当原始效应值是OR、风险比或相对风险度时，则应该先将估计值进行对数转换，因为后者更接近正态分布的渐近理论。

1.2 倒方差方法理论及介绍倒方差Meta方法通过对来自多个独立研究的点估计的加权平均，计算干预效应值的汇总估计来综合来自多个来源的信息。这种方法目前被广泛使用和推荐。对于NNM，倒方差的总体效应估计可通过下列公式获得

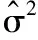
1.3 发病率密度数据的效应参数及计算发病率密度数据分为单臂研究和双臂研究。对于前者，研究人员关心的效应指标是发病率(IR)，而后者是IRR。

1.3.1 单臂研究IR的Meta分析对于单臂研究的IR密度数据背景下，每个研究中提供了事件Yi和总随访时间 Ti。每项研究的IR由Yi/Ti估算，而Meta分析的目的是估计总体IR。标准方法使用

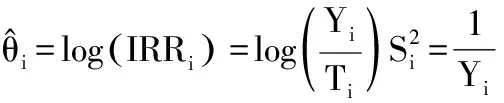
如果某项研究的对照组或干预组中存在0事件时，通常是两组分别增加0.5作“连续性校正”，尽管有学者提出可以使用其他数值进行校正[6-8]。计算出单个研究的效应值及其标准误后，可以根据上述NNM模型进行效应值的合并。

1.3.2 双臂研究IRR的Meta分析对于双臂研究，单项研究通常提供治疗组和对照组。Meta分析的效应值是IRR。令Yi0和Ti0为研究对照组中事件的数量和总的随访时间，类似地，治疗组为Yi1和Ti1。现在θi表示研究i的真实对数IRR，θ代表对应的总体平均值。标准的Meta分析模型可以使用

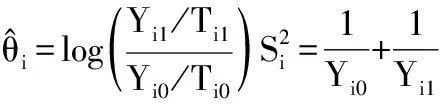
对于含0事件研究，同样需要上述校正方法进行校正。

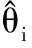
在单臂研究的发病率密度数据背景下，笔者主张用泊松分布代替正态分布：

Yi≃Poisson(Tiexp(θi)) 其中θi≃N(θ, σ2) (公式7)

PNM是具有偏移变量log(Ti)的随机截距泊松回归模型。

对于双臂研究的发病率密度数据背景下，对于研究i，事件总数Yi= Yi0+ Yi1，而Yi1被假设服从二项分布：

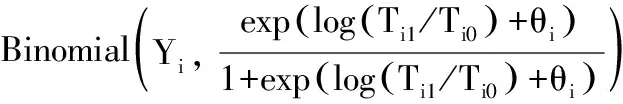
其中θi≃N(θ, σ2) (公式8)

BNM是一个随机截距逻辑回归模型，具有偏移量变量log(Ti1/Ti0)。

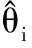
2 方法

2.1 待分析数据来源于Schutz等发表的研究血管内皮生长因子受体酪氨酸激酶抑制剂治疗的癌症患者发生致命不良事件(FAE)的风险[9]，“study”代表试验；“y1、n1、t1”分别代表治疗组的事件数、组样本量、中位生存时间；“y0、n0、t0”分别代表对照组的事件数、组样本量、中位生存时间(表1)。假设关心的结局：①不同干预组单位人时的总体事件发生率以中位总生存为基准，每1年总生存时间内的总体事件发生率；②比较两种干预对总体事件发生率的影响。

将表1的数据录入SAS软件，并存储在名为Example_data的数据集中(因篇幅限制，数据步的SAS代码简要输入)。在数据集中，存在2项单0试验，分别是study 3、study 10；3项双0试验，分别是study 1、study 5、study 6，分别对含0试验进行校正，校正后的数据保存在名为Example_data_CR的数据集。

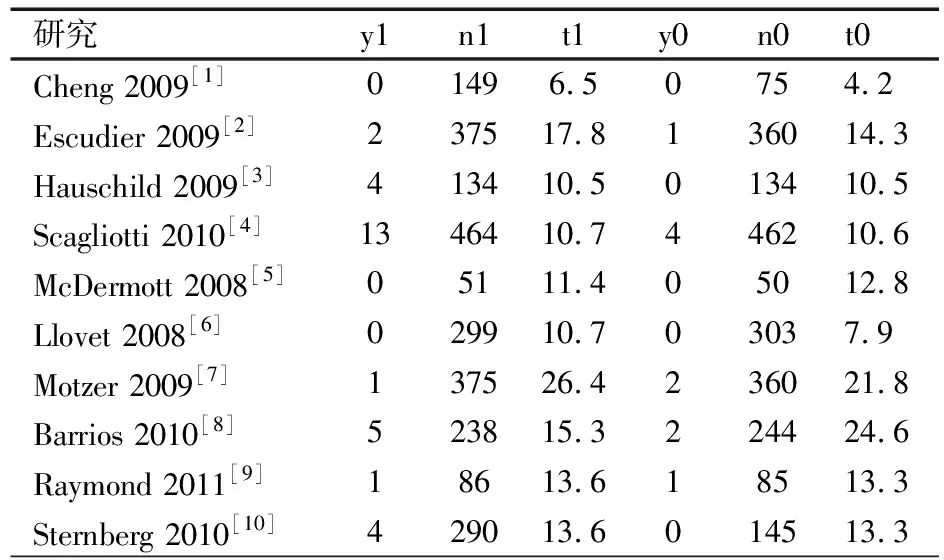
表1 待分析数据集

2.2 SAS代码介绍本文提供的附录代码包括数据集的录入，以及采用连续性校正的方法对数据集中的单0研究或双0研究进行校正，获得数据集Example_data_CR。然后使用PROC NLMIXED程序，实现NNM模型、BNM模型、PNM模型的Meta分析。

3 结果

3.1 不同干预组总体事件发生率的Meta分析结果表2显示，采用0.5对0事件进行校正后，NNM模型的Meta分析结果显示，研究组每1人年发生事件数0.719，对照组为0.564；而PNM模型研究组为0.594，对照组为0.419。正如前述，经过校正，研究组NNM模型每1人年事件发生数比PNM模型增加了17.4%，而对照组增加了25.7%，提示采用0.5校正的方法明显增加偏倚。此外，采用0事件研究删除的方法显示，NNM模型的Meta分析总体变化不大，以研究组为例，删除0事件研究后，每1人年发生事件数为0.721，与采用连续校正法相比，差异仅0.27%。但对于PNM模型，则变化较大，同样以研究组为例，删除0事件研究后，每1人年发生事件数为0.676，与采用连续校正法相比，差异仍达12.1%，提示删除0事件研究对PNM模型影响较大，反过来提示PNM具有较好的灵敏性。

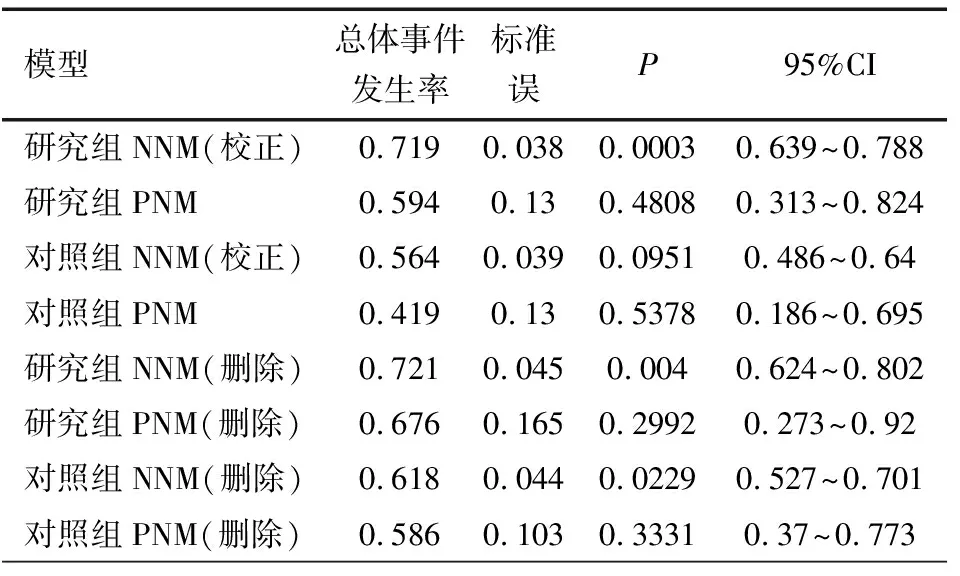
表2 不同干预组总体事件发生率的Meta分析结果

3.2 两种干预对总体事件发生率的影响的Meta分析结果表3显示，运行附录代码3后可以获得NNM模型和BNM模型的Meta分析结果。

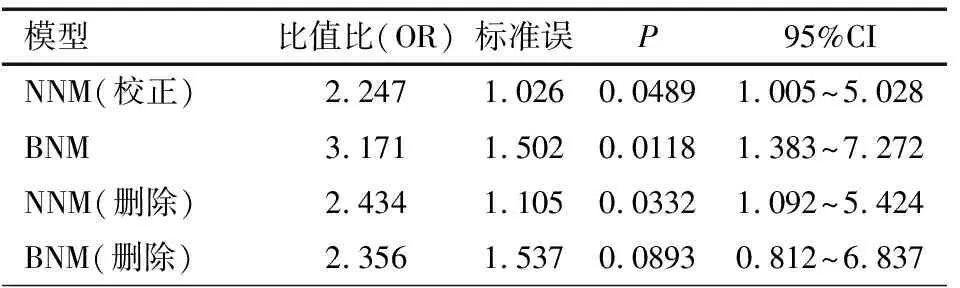
表3 不同干预组总体事件发生率的Meta分析结果

在表3中，NNM模型的Meta分析结果显示，采用连续性校正和0事件研究删除法，对效应值OR影响率为7.7%，影响率计算方法为[(2.434-2.247)/2.434]×100%，而BNM模型则高达25.70%{[(3.171-2.356)/2.356]×100%}。在该示例中，BNM模型给出总发生率的处理效应在幅度上稍微大于NNM模型，并且P值较小：NNM为0.0489，BNM方法为0.0118。BNM模型的效应值更高，而P值则更小，因此结果更灵敏、准确。根据表3中BNM模型的结果，可以认为VEGFR-TKIs治疗癌症患者发生致命不良事件(FAE)的风险大于对照组，其效应值OR=3.171，SE=1.502,95% CI：1.383～7.272。在这个例子中，BNM和NNM方法给出的跨研究标准差相似，但均<0.001，提示研究间差异很小(读者可以运行附录代码进行查看，这里不赘述)。

4 讨论

目前，关于发病率数据(随访资料中的事件数量)的Meta分析方法并未引起足够的重视[10]。当数据中存在0事件时，如何进行Meta分析仍然是一个悬而未决的问题[11]。尽管如此，越来越多的临床小样本研究需要进行Meta分析，以获得高质量的证据，尤其对某些新药开发中少见或罕见不良反应的发生率分析[11]。Spittal等[1]早已证明，当纳入分析的研究存在0事件时，采用倒方差方法获得的汇总结果是有偏差的，而这种方法却是最常用和最受推荐的方法之一。本文使用Cochrane手册推荐的连续性校正进行调整后，结果仍然存在偏倚风险[12]。

Guevara等提出使用泊松回归对每个研究的效应指标进行分析[3]。由于泊松分布包括0，对于含0事件研究而言，这种分布基础表明可以基于泊松分布进行发病率数据的Meta分析[1]。采用泊松分布进行Meta分析的关键问题是，基线变异性和异质性如何影响最终的总体IRR和其他固定效应估计[4]。理论上，该方法可以通过使用每个研究效应指标来解释基线变异性(即对照组中发病率的变化)。模拟数据表明，当基线变异性较低时，基于泊松分布的Meta分析方法可以产生相对无偏的估计[1, 5]，证明这种方法是行之有效的。本文使用Proc NLMIXED来实现基于PNM的Meta分析技术，对示例数据进行分析。在这个例子中，基于NNM模型和PNM模型拟合出的总体事件发生率存在比较大的的差异。正如预期的那样，采用连续性校正的传统方法的总体发病率略高，对照组和治疗组分别高25.7%和17.4%，进一步证明提示采用连续性校正的方法明显增加偏倚。

本文同时给出删除0事件研究的Meta分析结果。在实践中，这种方法是不推荐使用的[13]。对于研究组和对照组同时包含0事件时，通常从Meta分析中排除(这是许多统计软件的默认选项)。Cochrane手册认为，此类研究并未包含相关的OR/RR的信息，因此应予以排除[12]。然而，一些研究人员指出，从伦理的角度来看，双0研究中的患者应该被纳入分析[14]；而另一些人认为，这些研究可能通过样本量来提供相对治疗效果的信息[15]。笔示例分析表明，在BNM模型背景下，通过删除含0事件的研究，最终汇总效应值差别可高达25.7%，显然这是不可取的。

本文侧重在介绍Stijnen等提出的模型方法。结合提供的示例和Stijnen等的示例，证明基于BNM模型、PNM模型的Meta分析模型在SAS软件中可以很容易拟合。本文谨慎地推荐，对于发病率数据Meta分析，GLMM(即本文所述的BNM模型、PNM模型)应该成为优选技术。

附录代码1：资料录入

data Example_data;

input studyy1n1t1y0n0t0;

t0=t0/12; t1=t1/12; /*代表1人年的结果*/

datalines;

1 0 149 6.5 0 75 4.2

……

;

/*连续性校正*/

data Example_data_CR;

set Example_data;