某辅助动力装置燃油总管裂纹故障分析

邹子剑，李东杰，李继世，张大义

（1.中国航发湖南动力机械的研究所，湖南 株洲 412002；2.北京航空航天大学能源与动力学院，北京100083）

0 引言

某型辅助动力装置（APU）燃油总管在外场发生裂纹导致漏油，引起APU舱着火，严重影响飞行安全。故障发生时APU累计使用时间为40 h。通过对辅助动力装置燃油总管故障件断口分析以及对燃油总管的装配应力进行ANSYS仿真计算，对管路失效模式进行确认；并基于最小应变能定理，提出一种改进的装配方式，减小管路在装配时的应力。

1 燃油总管受力情况

燃油总管为聚四氟乙烯（PTFE）软管，内部结构示意如图1所示，软管由导电的PTFE内管、不锈钢丝增强层、金属连接件（接头、套筒、螺母）和硅橡胶防火套四部分组成[1]。

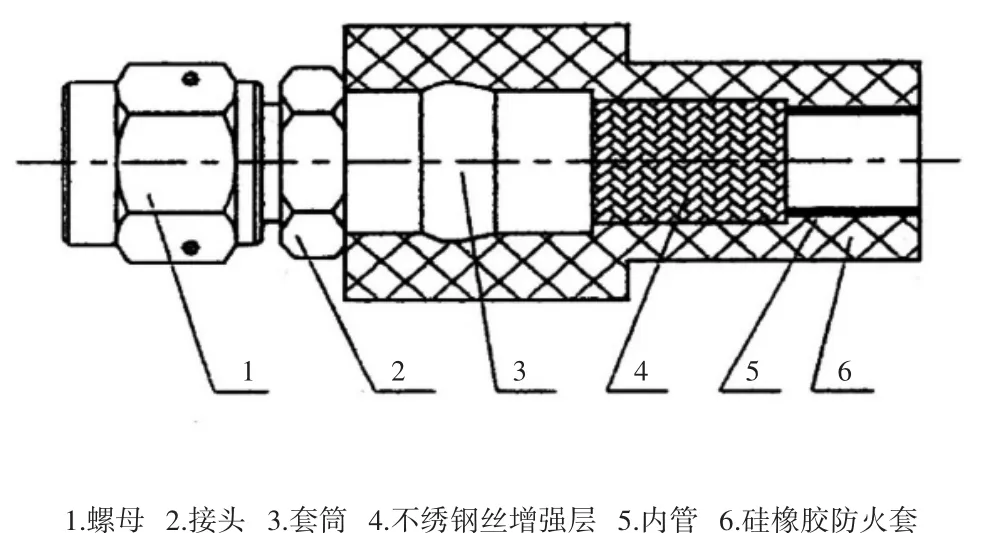
图1 燃油总管内部结构图

燃油总管沿APU燃烧室机匣周向装配，有14个均匀分布的装配点通向燃油喷嘴（装配点编号如图2所示，通过装配点编号指定相应的管段，如0-1段）。工作时燃油总管给14个喷嘴输送3号喷气燃料；燃油工作温度为-50～200℃，供油压力小于3 MPa，根据国军标[2-3]，该型管路属于低压软管。

在工作时，燃油总管主要承受以下3种应力：燃油总管内液体压力对燃油总管产生的应力，APU工作时燃油总管所受的振动应力，燃油总管装配时产生的初始装配应力。液体压力产生的应力由APU的工作状态决定，它对燃油总管产生的应力在一定范围内变化；燃油总管所受的振动应力由于燃油总管结构、布局未改变，在无共振影响时振动应力值变化不大，经测试燃油总管在正常工作转速下燃油总管没有产生共振；燃油总管所受的装配应力随燃油总管的长度、弯曲角度等装配参数变化，合适的装配参数将使燃油总管产生较小的装配应力，而不合适装配参数将可能使管路产生较大或很大的装配应力。

经初步分析，引起燃油总管裂纹的原因可能是承受的装配应力过大，因此本文将对某辅助动力装置燃油总管的装配应力进行分析。见图2。

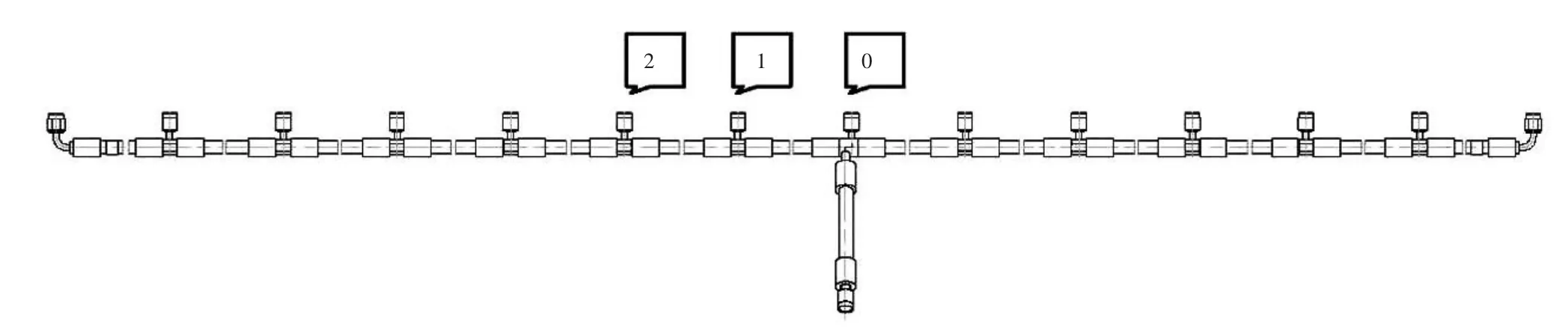
图2 燃油总管展开图

2 故障件断口检查

对故障管路进行裂纹和断口检查。检查中发现，燃油总管3-4段，靠近4号接头根部，金属接头与聚四氟乙烯管接触的位置出现2 mm的周向裂纹，开口与金属编制网的压痕形貌类似，见图3（a），该裂纹位于弯曲最严重的外侧，见图3（b），疲劳弧线位于聚四氟乙烯断口上，沿着周向往两侧均匀扩展，可基本确定源区位于两侧弧线对称的中间区域，见图4（a~b）。细观下，同时可见由内向外以及沿周向扩张的疲劳弧线，源区位于聚四氟乙烯管的内侧，见图5。

图3 聚四氟乙烯管周向裂纹以及对应位置

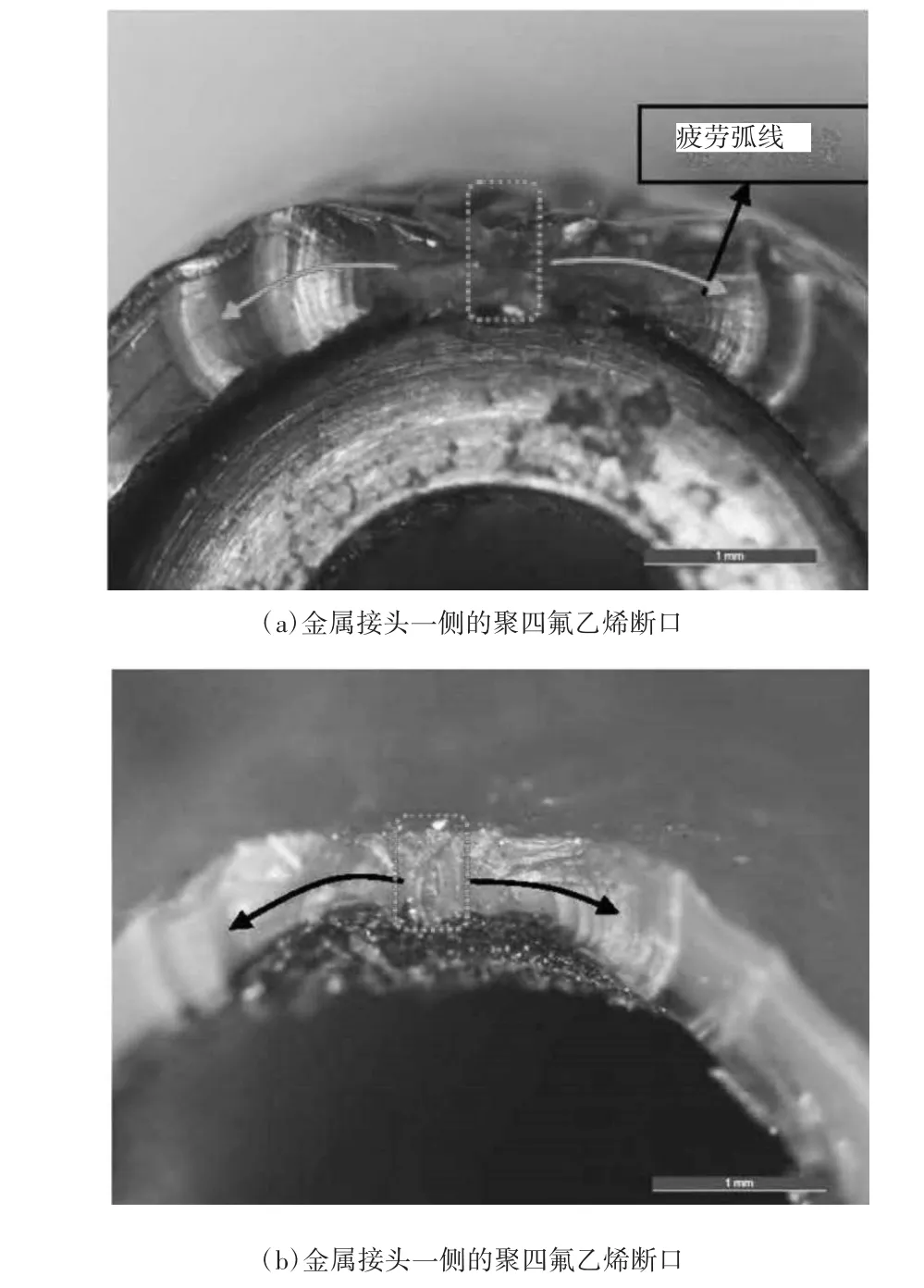
图4 断口宏观形貌

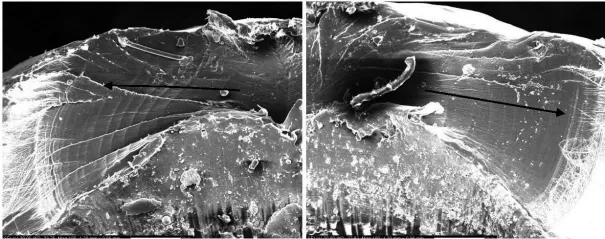
图5 断口细观形貌

3 聚四氟乙烯管裂纹机理分析

一般而言，聚四氟乙烯管的微裂纹和静电击穿是导致管体泄露的主要原因[4]，而该软管不存在静电击穿的问题。对于PTFE内管裂纹，作为传输介质的接触载体，其管体必须是无裂纹的（非透过性裂缝）。裂纹早期称为银纹，在一些半晶体的聚合物中，由于应力及环境因素的影响，会在材料表面或内部出现微小但相对密集的银纹，银纹现象是高聚物在张力作用下，在材料某些薄弱部位出现应力集中而产生局部塑性形变和局部取向[5]。造成聚四氟乙烯管裂纹的原因可分为外因和内因。

外因主要是由于压力软管装配不规范而导致的管体渗漏，如管体扭曲装配、压力弯曲半径小于标准要求。一方面扭曲或弯曲半径过小本身会带来比较大的初始装配应力；另一方面软管耐压能力与装配弯曲半径有关，软管充压后，通过聚四氟乙烯内管将压力传递给钢丝编织层，软管弯曲时，钢丝编织角度发生变化，使软管径向应力与轴向应力的均衡力方向同钢丝层的编织方向不一致，软管耐压力下降，软管弯曲半径越小，则耐压强度下降越多[6]。因此装配软管时，尽可能使弯曲半径大一些，一般不应小于20 D，在无法保证时，也不能小于胶管的最小弯曲半径（一般为10 D）。

内因多数是由于成型时操作不当所致，如推压成型或增强编织时，PTFE内管内部的推压或编织芯棒造成的内管内壁划痕；或由于烧结不充分，造成的颗粒之间粘结力下降，而产生的管体银纹现象[7-8]。

4 燃油总管装配应力分析

根据断口显微检查结果，在燃油总管金属接头位置处的聚四氟乙烯管存在疲劳裂纹，软管内部结构图见图6。图6中的蓝色件为金属接头，疲劳裂纹发生在内管与金属接头的接触处，即红圈处。根据聚四氟乙烯内管的机理分析分析和燃油总管承制厂商的复查，可以排除由成型不当造成的裂纹，基本判定疲劳裂纹产生的主要原因是装配方式不正确，造成内管与金属接头接触处局部应力过大，并造成软管耐压能力下降。本节对燃油总管的装配应力进行分析。

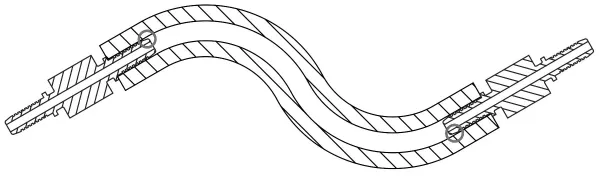
图6 软管疲劳裂纹位置

4.1 管路主要装配参数的选取

燃油总管的装配效果如图7所示。

图7 燃油总管装配情况

根据燃油总管的装配情况，可建立燃油总管装配状态的模型如图8所示。经简化后，认为影响装配效果的主要参数为下列4个：

（1）软管自由伸长的长度L；

（2）两个装配支点的跨度l；

（3）支点 1 装配角度 θ1；

（4）支点 2 装配角度 θ2。

由于装配节点间距l由燃烧室的尺寸和燃油喷嘴的位置所决定，因为管路自由伸长长度L无法改变，所以实际可控的装配参数只有两个：即支点1装配角度θ1和支点2装配角度θ2。测得燃油总管的装配点的直线距离l=91.45 mm，管路自由伸长的长度为L=95.5 mm。

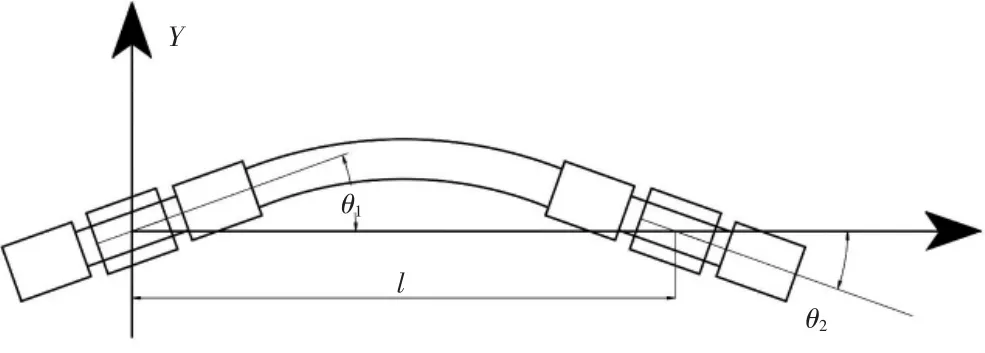
图8 管路装配参数模型

4.2 原因分析与改进方案

实际总管的装配情况如图9所示，可以认为该装配方式支点1、2的装配角度θ1和θ2相等，即θ1=θ2，此时软管在两个支点之间呈S型，装配变形比较大，即管路的弯曲半径较小。管路装配时，控制软管装配形状的主要是两端金属接头的装配角度θ1和θ2，也就是支点1、2的装配角度，因此控制软管变形的外力主要来源于金属接头与内管内壁面的接触应力，可以看出，该种装配方式下，主要的应力集中区域在红圈处，这与内管疲劳裂纹的位置吻合。后文会作计算验证。

引起该接触应力过大的原因是管路装配状态的弯曲曲率过大。为了减小应力水平必须减小弯曲曲率，具体方法是改变装配方式。对于改进的装配方式，金属接头的装配角度不应保持同向（θ1=θ2），而应做周期性地变化（θ1=-θ2），以减少管路的装配曲率，从而减少装配应力。如图10所示。

图9 实际装配方式

图10 改进装配方式

4.3 计算验证

下面分别计算现在装配方式以及改进装配方式的装配应力水平，利用ANSYS软件计算验证改进方案的应力水平减小情况。假设现有装配方式的装配角度 θ1=30°，θ2=30°，而改进装配方式的装配角度θ1=30°，θ2=-30°。

计算验证主要是验证改进方式的效果，并不是计算具体的局部接触应力，因此在计算中考虑三层不同的材料，但是不考虑各层之间的相对运动，认为是一体结构。图11中蓝色为PTFE内管，灰色为金属加强网，棕色为防火套。

图11ANSYS管路网格模型

当装配角度为 θ1=30°，θ2=30°（对应现有装配方式）时，等效应力最大值为173.56 MPa，等效应力云图如图 12；当装配角度为 θ1=30°，θ2=-30°（对应改进装配方式）时，等效应力最大值为76.398 1 MPa，等效应力云图如图13。

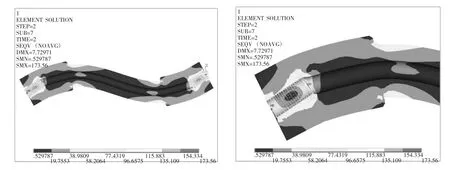
图12 现有装配方式应力分布情况

图13 改进装配方式应力分布情况

根据两种装配方案的计算结果可以发现，等效最大应力发生的部位在金属接头的一端与内管的接触处，位于弯曲最严重的外侧。这与燃油总管内管疲劳裂纹发生的位置吻合，说明装配应力是引起内管疲劳裂纹的主要原因之一。另外也可以验证，改进装配方案相比于现用的装配方案，应力水平大幅度减少。原方案的局部应力为173.56 MPa，改进方案为76.398 1 MPa，减少了56%，实现的方法是增大弯曲半径。

进一步分析，因为管路本身装配时会变形，即存在应变能，在弹性力学中具体指拉压应变能以及弯曲应变能，装配时的应变能水平一定程度上决定了装配应力。因为应变能越大，说明系统中存储了越多的势能，其恢复自由伸长状态的趋势越强，从而对于在约束管路变形的金属接头与内管的接触面上造成更大的应力。如果认为管路自由伸长的长度不变，且两端支点距离不变，管路的曲率越大，一般可以认为其拉压应变能和弯曲应变能越大，这解释了增大弯曲半径减小装配应力的机理。

5 管路最佳装配方式的分析

管路最佳装配方式的评价标准是使得管路装配应变能最小，而装配应力水平可通过装配后管路总的应变能U=UT+UM表征，其中UT为拉压应变能，UM为弯曲应变能。

对于材料参数、截面尺寸以及软管完全自由伸长长度L给定的燃油总管，总应变能U只取决于装配后管路的形状，如图8所示，可以用管路轴线函数y=f（x）x∈[0，l]描述管路的形状，其中 l为装配节点间距，支点1装配角度θ1，支点2装配角度θ2。

管路轴线函数y=f（x）可认为是一个4次多项式函数，共有5个系数，通过以下5个条件完全确定：

（1）在支点 1 处固定即 y（0）=0；

（2）在支点 2 处固定即 y（l）=0；

（3）支点 1 的装配角度 dy/dx│x=0=tan（θ1）；

（4）支点 2 的装配角度 dy/dx│x=l=tan（θ2）；

（5）根据最小能量原理，在装配状态，软管的变形（应力-应变）情况一定遵循使得总的应变能U=UT+UM处于极小值的原则。

根据以上的5个条件，可确定4次多项式函数的5个系数，即确定管路装配后的轴线（形状），进而确定装配总应变能，同时反映了装配的应力水平。

通过条件（1）和条件（2），可将管路轴线函数y=f（x）写成多项式形式：

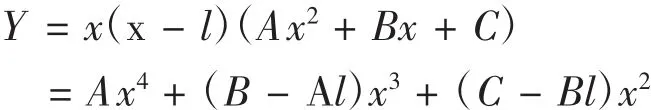
引入两个边界条件：管路两端的装配角θ1，θ2：

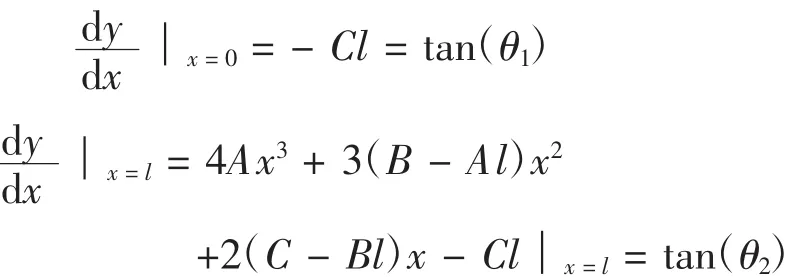
管路的总应变能：

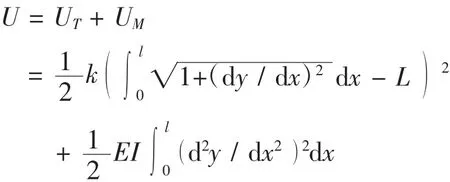
泰勒展开得到：

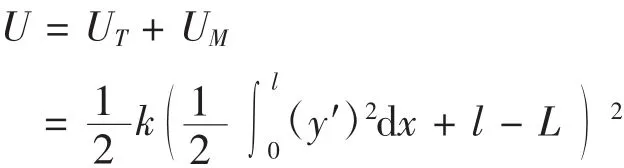
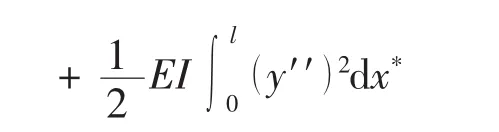
根据泛函极值定理，则有δU=0，并且可以认为，泛函取极值一定是极小值，不会有极大值，因为总应变能没有上界，推知：

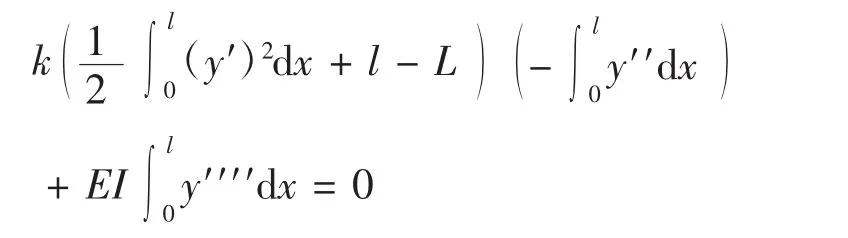
通过以上分析，给定装配角度，即支点1装配角度θ1和支点2装配角度θ2确定时，管路轴线函数y=f（x）也确定。下面给出一些典型装配角度时的管路轴线形状。

当 θ1=0°，θ2=0°，管路没有弯曲变形（如图14），符合一般性的认知。

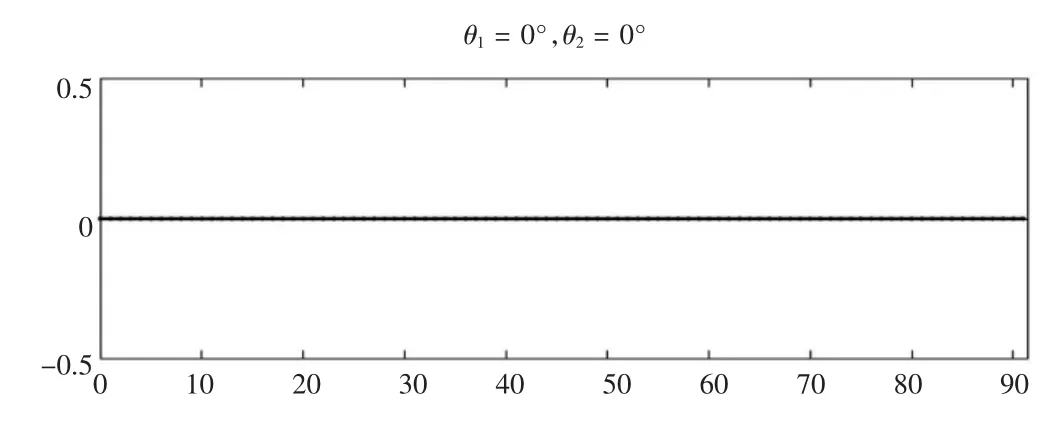
图14 当θ1=0°，θ2=0°管路变形情况

当 θ1=30°，θ2=30°，管路呈现出波浪线的形状（如图15），即实际装配方式。

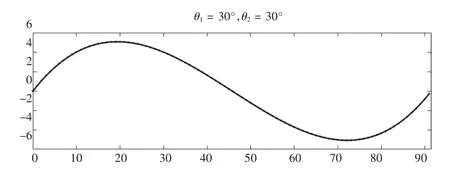
图15 当θ1=30°，θ2=30°管路变形情况

当 θ1=30°，θ2=-30°，管路呈现出类似抛物线的形状（如图16），即改进装配方式。

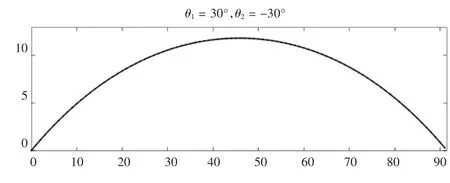
图16 当θ1=30°，θ2=-30°管路变形情况

进一步根据式（*）可以建立起装配总应变能U与装配角度 θ1和 θ2的关系 U=g（θ1，θ2）。图 17 等高线图表明了装配角度对总应变能（红高蓝低）的影响，可见如果按照原方案装配，即装配角度θ1=θ2，对应图17中的次对角线，应变能水平总体偏高，而且随着装配角度绝对值变大而增大。而如果按照本文提出的改进装配方案，即装配角度θ1=θ2，对应图17中的主对角线，可以实现更低的装配应变能水平，即更低的装配应力水平。

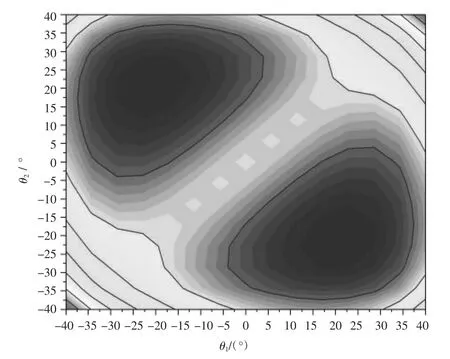
图17 总应变能与装配角度θ1和θ2的关系

根据图17的结果，应该尽可能将装配角度设计在图中的深蓝色区域。对于本文研究的管路，其最佳的装配角度是 θ1=-θ2=22.857 14°

在ANSYS中进行计算验证，得到表1。

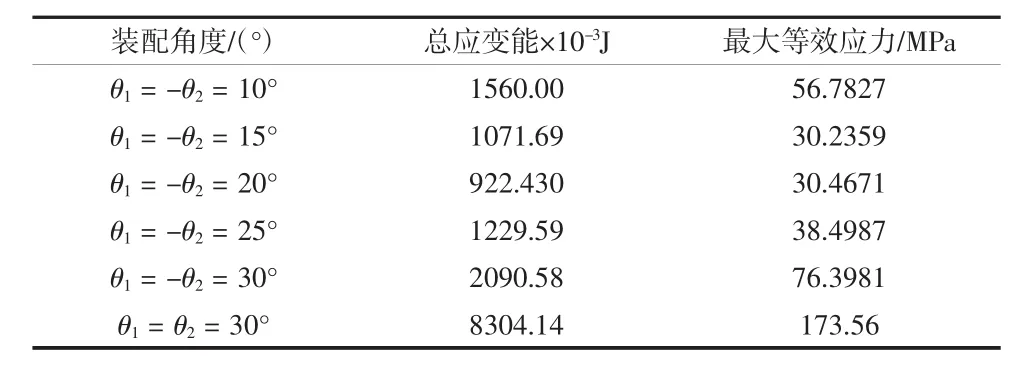
表1 装配角度与总应变能及最大等效应力的关系

根据表1可知：

1）利用总应变能可以在一定程度上反映最大等效应力；

2）改进方式的装配角度即θ1=-θ2优于现用的装配角度即 θ1= θ2；

3）理论推导的最佳装配角基本符合ANSYS使用实体单元仿真计算的结果。理论计算的最佳装配角度是 θ1=-θ2=22.857 14°，而 ANSYS 仿真结果表明，最小总应变能的装配角在θ1=-θ2=20°左右。

6 结论

（1）通过有限元分析与计算，确定某辅助动力装置燃油总管产生裂纹故障主要原因是管路装配时装配角度不合理，导致早期装配应力过大。在外场振动、冲击等综合工况作用下引发裂纹的萌生。

（2）在燃油总管自由伸长的长度无法随意变更的前提下，可采用本文中改进管路装配角度的方案，来改善在装配时的应力集中。